In English
Общее поле
Из
проекта Викизнание
Компоненты
общего поля
Общее поле — физическое поле, компонентами которого являются электромагнитное и гравитационное поля, поле ускорений, поле давления, поле диссипации, поле сильного взаимодействия, поле слабого взаимодействия, а также другие векторные поля, действующие на вещество и его частицы. Таким образом, общее поле проявляется через свои компоненты и не равно нулю, пока существует хотя бы одна из этих компонент. Фундаментальные взаимодействия, к которым относятся электромагнитное, гравитационное, сильное и слабое взаимодействия, происходящие в веществе, оказываются частью взаимодействий, описываемых общим полем.
Концепция общего поля появилась в рамках метрической теории относительности и ковариантной теории гравитации как обобщение процедуры для нахождения тензора энергии-импульса и уравнений векторного поля любого вида. [1] С помощью этой процедуры из принципа наименьшего действия были выведены вначале уравнения гравитационного поля, [2] [3] [4] затем уравнения поля ускорений и поля давления, [5] а потом уравнения поля диссипации энергии за счёт вязкости. [6] Все эти уравнения по своей форме оказываются подобными уравнению Максвелла. Это означает, что в сущности каждого векторного поля содержится нечто общее, объединяющее его с другими полями. Отсюда вытекает идея общего поля, описанная в статъях Сергея Федосина. [7] [8]
Теория
общего поля представляет собой один из вариантов не квантовой единой теории
поля, и является в том числе одной из теорий Великого объединения.
Оглавление
|
Обозначения частных полей и полевых функций
В Таблице 1 представлены обозначения для всех тех полей,
которые являются компонентами общего поля.
|
Таблица 1. Обозначения полевых функций |
||||||||
|
Функция поля |
Электромагнитное поле |
Гравитационное поле |
Поле ускорений |
Поле давления |
Поле диссипации |
Поле сильного взаимодействия |
Поле слабого взаимодействия |
Общее поле |
|
4-потенциал
|
|
|
|
|
|
|
|
|
|
Скалярный
потенциал |
|
|
|
|
|
|
|
|
|
Векторный
потенциал |
|
|
|
|
|
|
|
|
|
Напряжённость
поля |
|
|
|
|
|
|
|
|
|
Соленоидальный
вектор |
|
|
|
|
|
|
|
|
|
Тензор
поля |
|
|
|
|
|
|
|
|
|
Тензор
энергии-импульса |
|
|
|
|
|
|
|
|
|
Вектор
потока энергии-импульса |
|
|
|
|
|
|
|
|
|
Постоянная
поля |
|
|
|
|
|
|
|
|
В Таблице 1 вектор ![]() есть вектор Пойнтинга, вектор
есть вектор Пойнтинга, вектор ![]() – вектор
Хевисайда.
– вектор
Хевисайда.
Математическое описание
В ковариантной теории гравитации основным представителем любого векторного поля является его 4-потенциал, с помощью которого выражаются все остальные функции поля. Поскольку общее поле существует через свои компоненты в виде отдельных частных полей, 4-потенциал общего поля является суммой 4-потенциалов частных полей, в соответствии с принципом суперпозиции для этих полей:
![]()
По
своему смыслу 4-потенциал ![]() является обобщённой 4-скоростью. [9]
является обобщённой 4-скоростью. [9]
Так как 4-потенциал любого поля состоит из скалярного и векторного потенциалов, то скалярный потенциал общего поля есть сумма скалярных потенциалов частных полей, и то же самое следует в отношении векторных потенциалов:
![]()
![]()
Тензор
общего поля вычисляется как 4-ротор от 4-потенциала. Если считать, что
отношение плотности заряда к плотности массы
![]() в каждом рассматриваемом элементе вещества
постоянно и равно отношению заряда к массе элемента вещества, тензор общего
поля оказывается суммой тензоров частных полей:
в каждом рассматриваемом элементе вещества
постоянно и равно отношению заряда к массе элемента вещества, тензор общего
поля оказывается суммой тензоров частных полей:
![]()
Компонентами тензоров поля являются их напряжённости и соленоидальные векторы. Следовательно, напряжённость общего поля в каждом элементе вещества (в элементе объёма) есть сумма напряжённостей частных полей, и аналогично будет для соленоидального вектора общего поля:
![]()
![]()
Действие, Лагранжиан и энергия
В
рамках ковариантной теории гравитации
вещество характеризуется массовым 4-током
![]() , где
, где ![]() есть 4-скорость. При этом зарядовый 4-ток
получается с помощью массового 4-тока
есть 4-скорость. При этом зарядовый 4-ток
получается с помощью массового 4-тока ![]() из соотношения:
из соотношения:
![]()
Вследствие
этого плотность энергии взаимодействия общего поля с веществом задаётся
произведением 4-потенциала общего поля на массовый 4-ток: ![]() .
Другой тензорный инвариант, в виде
.
Другой тензорный инвариант, в виде ![]() , с точностью до постоянного
коэффициента пропорционален плотности энергии общего поля. Функция действия,
содержащая скалярную кривизну
, с точностью до постоянного
коэффициента пропорционален плотности энергии общего поля. Функция действия,
содержащая скалярную кривизну ![]() и космологическую постоянную
и космологическую постоянную ![]() ,
определяется выражением:
,
определяется выражением:
![]()
где ![]() – функция Лагранжа или лагранжиан,
– функция Лагранжа или лагранжиан, ![]() –
дифференциал времени координатной системы отсчёта,
–
дифференциал времени координатной системы отсчёта, ![]() и
и ![]() – постоянные, подлежащие определению,
– постоянные, подлежащие определению, ![]() – скорость света, как мера скорости
распространения электромагнитного и гравитационного взаимодействий,
– скорость света, как мера скорости
распространения электромагнитного и гравитационного взаимодействий, ![]() – инвариантный 4-объём, выражаемый через
дифференциал временной координаты
– инвариантный 4-объём, выражаемый через
дифференциал временной координаты ![]() ,
через произведение
,
через произведение ![]() дифференциалов пространственных координат, и
через квадратный корень
дифференциалов пространственных координат, и
через квадратный корень ![]() из детерминанта
из детерминанта
![]() метрического тензора, взятого с отрицательным
знаком.
метрического тензора, взятого с отрицательным
знаком.
Вариация
![]() функции действия
состоит из суммы членов, содержащих:
функции действия
состоит из суммы членов, содержащих:
1)
вариацию ![]() 4-потенциала
общего поля;
4-потенциала
общего поля;
2)
вариацию координат ![]() , создающую вариацию
, создающую вариацию ![]() массового 4-тока;
массового 4-тока;
3)
вариацию ![]() метрического тензора.
метрического тензора.
В силу
принципа наименьшего действия, вариация ![]() должна обращаться в нуль. Это приводит к
равенству нулю сумм всех членов, стоящих перед вариациями
должна обращаться в нуль. Это приводит к
равенству нулю сумм всех членов, стоящих перед вариациями ![]() ,
,![]() и
и ![]() ,
соответственно. Как следствие, отсюда вытекают уравнения общего поля,
четырёхмерное уравнение движения и уравнение для определения метрики.
,
соответственно. Как следствие, отсюда вытекают уравнения общего поля,
четырёхмерное уравнение движения и уравнение для определения метрики.
По определению интеграл функции действия должен быть
суммой интегралов по 4-объёму по всем элементам вещества и по всему объёму,
занимаемому полями. Во многих случаях физическая система содержит элементы
вещества, в которых отношение ![]() отличается от среднего значения. В этом
случае уравнения для поля, движения вещества и метрики будут зависеть не только
от локального отношения
отличается от среднего значения. В этом
случае уравнения для поля, движения вещества и метрики будут зависеть не только
от локального отношения ![]() , но и от отношения заряда к
массе в других элементах вещества, что
реализуется через суммарное поле этих элементов вещества.
, но и от отношения заряда к
массе в других элементах вещества, что
реализуется через суммарное поле этих элементов вещества.
Лагранжиан
представляет собой интеграл по объёму от суммы членов с размерностью плотности
энергии и по составу своих компонент подобен гамильтониану, задающему энергию
системы. Действительно, гамильтониан получается из лагранжиана с помощью
преобразования Лежандра для системы частиц. Как известно, энергия определяется
с точностью до константы, то есть энергия подлежит калибровке. Например,
энергия электромагнитного поля калибруется так, что на бесконечности
относительно заряда плотность энергии электромагнитного поля равна нулю. Точно
также подлежит калибровке энергия системы в виде гамильтониана. В ковариантной
теории гравитации принимается, что калибровочным членом является
космологическая постоянная ![]() . По
своему смыслу она с точностью до постоянного коэффициента представляет собой ту
плотность энергии, которую имеет система после того, как всё вещество системы
разделено на отдельные частицы и разнесено на бесконечность. В этом случае
исчезает энергия взаимодействия частиц друг с другом посредством полей, и
остаётся лишь собственная энергия частиц как энергия их собственных полей при
нуле температуры. Условие калибровки космологической постоянной имеет вид:
. По
своему смыслу она с точностью до постоянного коэффициента представляет собой ту
плотность энергии, которую имеет система после того, как всё вещество системы
разделено на отдельные частицы и разнесено на бесконечность. В этом случае
исчезает энергия взаимодействия частиц друг с другом посредством полей, и
остаётся лишь собственная энергия частиц как энергия их собственных полей при
нуле температуры. Условие калибровки космологической постоянной имеет вид:
![]()
При выполнении условия калибровки космологической постоянной энергия системы перестаёт зависеть от члена со скалярной кривизной и становится однозначно определённой:
![]()
где ![]() и
и ![]() обозначают временные компоненты 4-векторов
обозначают временные компоненты 4-векторов ![]() и
и ![]() .
.
Уравнения
Уравнения общего поля имеют следующий вид:
![]()
![]()
Таким
образом, единственным источником общего поля предполагается массовый 4-ток ![]() .
Последнее уравнение можно записать более кратко с помощью символа Леви-Чивиты
или совершенно антисимметричного единичного тензора:
.
Последнее уравнение можно записать более кратко с помощью символа Леви-Чивиты
или совершенно антисимметричного единичного тензора:
![]()
Подставляя (1), можно выразить уравнения общего поля через тензоры частных полей:


В
состоянии равновесия можно считать, что уравнение (5) выполняется отдельно для
тензора каждого поля, а не только для всей суммы тензоров частных полей. Точно
так же, при условии ![]() уравнение (4) может быть разбито на 7
отдельных уравнений, в которых массовый 4-ток
уравнение (4) может быть разбито на 7
отдельных уравнений, в которых массовый 4-ток ![]() является источником того или иного поля.
является источником того или иного поля.
Условие калибровки 4-потенциала общего поля:
![]()
В
искривлённом пространстве-времени уравнения поля дают равенство:
![]()
Вторая
часть этого равенства обнуляется ввиду симметричности тензора Риччи ![]() и
антисимметричности тензора
и
антисимметричности тензора ![]() .
Отсюда следует уравнение непрерывности в виде
.
Отсюда следует уравнение непрерывности в виде ![]() .
В пространстве Минковского специальной теории относительности ковариантная
производная
.
В пространстве Минковского специальной теории относительности ковариантная
производная ![]() превращается
в 4-градиент
превращается
в 4-градиент ![]() ,
так что уравнение непрерывности упрощается:
,
так что уравнение непрерывности упрощается:
![]()
Уравнение движения элемента вещества в общем поле описывается формулой:
![]() .
.
Так как
![]() , а тензор общего поля выражается через
тензоры частных полей, то уравнение движения можно представить через эти
тензоры:
, а тензор общего поля выражается через
тензоры частных полей, то уравнение движения можно представить через эти
тензоры:
![]()
Здесь ![]() – тензор ускорений,
– тензор ускорений, ![]() – тензор
электромагнитного поля,
– тензор
электромагнитного поля, ![]() – тензор гравитационного поля,
– тензор гравитационного поля, ![]() – тензор
поля давления,
– тензор
поля давления, ![]() – тензор поля диссипации,
– тензор поля диссипации, ![]() – тензор поля сильного взаимодействия,
– тензор поля сильного взаимодействия, ![]() – тензор поля слабого взаимодействия.
– тензор поля слабого взаимодействия.
Тензор энергии-импульса
Тензор энергии-импульса общего поля определяется из принципа наименьшего действия выражением
![]()
Через этот тензор уравнение движения записывается в очень простой форме, как равенство нулю дивергенции тензора:
![]() .
.
Тензор энергии-импульса общего поля входит в уравнение для метрики:
![]()
где ![]() – гравитационная
постоянная,
– гравитационная
постоянная, ![]() – некоторая
постоянная, и использовано условие калибровки космологической постоянной.
– некоторая
постоянная, и использовано условие калибровки космологической постоянной.
Тензор
общего поля ![]() имеет своими
компонентами напряжённость
имеет своими
компонентами напряжённость ![]() и соленоидальный вектор
и соленоидальный вектор ![]() общего поля. Вектор
общего поля. Вектор ![]() согласно (2) является суммой напряжённостей
частных полей, а вектор
согласно (2) является суммой напряжённостей
частных полей, а вектор ![]() согласно (3) состоит из соленоидальных
векторов частных полей. В тензоре энергии-импульса общего поля
согласно (3) состоит из соленоидальных
векторов частных полей. В тензоре энергии-импульса общего поля ![]() имеется тензорное произведение
имеется тензорное произведение ![]() ,
так что тензор
,
так что тензор ![]() содержит квадраты
векторов
содержит квадраты
векторов ![]() и
и ![]() .
Заменяя эти векторы на суммы соответствующих векторов частных полей, приходим к
следующему:
.
Заменяя эти векторы на суммы соответствующих векторов частных полей, приходим к
следующему:
![]()
где ![]() – некоторые коэффициенты,
– некоторые коэффициенты, ![]() – тензор энергии-импульса электромагнитного
поля,
– тензор энергии-импульса электромагнитного
поля, ![]() – тензор энергии-импульса гравитационного поля,
– тензор энергии-импульса гравитационного поля,
![]() – тензор энергии-импульса поля ускорений,
– тензор энергии-импульса поля ускорений, ![]() – тензор
энергии-импульса поля давления,
– тензор
энергии-импульса поля давления, ![]() – тензор
энергии-импульса поля диссипации,
– тензор
энергии-импульса поля диссипации, ![]() – тензор энергии-импульса поля сильного
взаимодействия,
– тензор энергии-импульса поля сильного
взаимодействия, ![]() – тензор
энергии-импульса поля слабого взаимодействия.
– тензор
энергии-импульса поля слабого взаимодействия.
Как
видно, тензор энергии-импульса общего поля ![]() содержит не только тензоры энергии-импульса
частных полей, но и перекрёстные члены с произведениями напряжённостей и
соленоидальных векторов частных полей.
содержит не только тензоры энергии-импульса
частных полей, но и перекрёстные члены с произведениями напряжённостей и
соленоидальных векторов частных полей.
Для примера, если учитывать только гравитационное поле и поле ускорений, для тензора энергии-импульса общего поля получается:
![]()
![]()
где ![]() – постоянная, входящая в определение тензора
энергии-импульса поля ускорений.
– постоянная, входящая в определение тензора
энергии-импульса поля ускорений.
Разделение на две компоненты
В статье [8]
общее поле было разделено на две основные компоненты. Одна из них – массовая компонента
общего поля, источником которой является массовый 4-ток ![]() .
Вторая, зарядовая компонента общего поля, имеет в качестве источника зарядовый
4-ток
.
Вторая, зарядовая компонента общего поля, имеет в качестве источника зарядовый
4-ток ![]() .
Массовая компонента общего поля содержит в себе гравитационное поле, поле
ускорений, поле давления, поле диссипации, поля сильного и слабого
взаимодействия, другие векторные поля. Зарядовая компонента общего поля
представляет собой электромагнитное поле. В результате разделения общего поля
на две компоненты уравнения полей стали более независимыми друг друга, так как
условие неизменности отношения зарядовой инвариантной плотности к массовой
инвариантной плотности
.
Массовая компонента общего поля содержит в себе гравитационное поле, поле
ускорений, поле давления, поле диссипации, поля сильного и слабого
взаимодействия, другие векторные поля. Зарядовая компонента общего поля
представляет собой электромагнитное поле. В результате разделения общего поля
на две компоненты уравнения полей стали более независимыми друг друга, так как
условие неизменности отношения зарядовой инвариантной плотности к массовой
инвариантной плотности ![]() теперь не требуется. Для обозначения функций
поля массовой компоненты общего поля далее используются те же обозначения,
которые в Таблице 1 указаны для самого общего поля.
теперь не требуется. Для обозначения функций
поля массовой компоненты общего поля далее используются те же обозначения,
которые в Таблице 1 указаны для самого общего поля.
4-потенциалом
зарядовой компоненты общего поля является электромагнитный 4-потенциал ![]() . 4-потенциал массовой компоненты общего поля
равен сумме 4-потенциалов соответствующих полей:
. 4-потенциал массовой компоненты общего поля
равен сумме 4-потенциалов соответствующих полей:
![]()
Аналогично,
скалярный и векторный потенциалы массовой компоненты общего поля будут равны:
![]()
![]()
Вместо (1),
(2) и (3) для тензора, напряжённости и соленоидального вектора массовой
компоненты общего поля будет следующее:
![]()
![]()
![]()
Тензором
зарядовой компоненты общего поля является электромагнитный тензор:
![]()
состоящий из
компонент напряжённости электромагнитного поля ![]() и компонент магнитного поля
и компонент магнитного поля ![]() .
.
Потенциалы,
напряжённости и соленоидальные векторы частных полей для сферического тела были
вычислены в статье, [10] а также в других статьях. [6] [11]
[12] [13]
Функция
действия и энергия системы определяются так:
![]()
![]()
По своему построению общее поле является векторным полем, так что для него будет справедливо каждое уравнение векторного поля.
Уравнения
для тензоров массовой и зарядовой компонент общего поля будут следующие:
![]()
![]()
![]()
![]()
Условия
калибровки 4-потенциалов компонент общего поля:
![]()
![]()
Уравнения
непрерывности для соответствующих 4-токов в искривлённом пространстве-времени:
![]()
![]()
Уравнение
движения вещества под действием полей:
![]()
Уравнение
движения можно также записать через тензор энергии-импульса электромагнитного
поля ![]() и
тензор энергии-импульса массовой компоненты общего поля
и
тензор энергии-импульса массовой компоненты общего поля ![]() :
:
![]()
Указанные
тензоры с контравариантными индексами определяются так:
![]()
![]()
Уравнение
для метрики:
![]()
В статье [14]
было показано, что для коэффициентов полей, входящих в массовую компоненту общего
поля, должно быть справедливо соотношение:
![]()
где ![]() есть постоянная поля ускорений,
есть постоянная поля ускорений, ![]() – постоянная поля давления,
– постоянная поля давления, ![]() –
гравитационная постоянная,
–
гравитационная постоянная, ![]() – постоянная поля диссипации, [6]
– постоянная поля диссипации, [6] ![]() – постоянная макроскопического поля сильного
взаимодействия, [7]
– постоянная макроскопического поля сильного
взаимодействия, [7] ![]() – постоянная макроскопического поля слабого
взаимодействия.
– постоянная макроскопического поля слабого
взаимодействия.
Для случая релятивистской
однородной системы тензоры полей, входящих в массовую
компоненту общего поля, оказываются пропорциональны друг другу. [15]
[10] С учётом этого, тензор
энергии-импульса массовой компоненты общего поля выражается через тензоры
энергии-импульса частных полей, при этом перекрёстные члены исчезают:
![]()
Частные решения для функций общего поля
В стационарном
случае можно предположить, что энергия в системе распределяется в соответствии
с теоремой о равнораспределении. В силу этой теоремы, для систем, находящихся в
тепловом равновесии в условиях, когда квантовые эффекты не играют ещё большой
роли, любая степень свободы ![]() частицы, делающая вклад в энергию в виде
степенной функции
частицы, делающая вклад в энергию в виде
степенной функции ![]() , имеет в среднем одну и ту же энергию
, имеет в среднем одну и ту же энергию ![]() ,
где
,
где ![]() – постоянная
Больцмана,
– постоянная
Больцмана, ![]() – температура. У частиц идеального газа есть
только три таких степени свободы – это три компоненты скорости, входящие
квадратично в кинетическую энергию (
– температура. У частиц идеального газа есть
только три таких степени свободы – это три компоненты скорости, входящие
квадратично в кинетическую энергию (![]() ,
, ![]() )
, поэтому средняя энергия частицы равна
)
, поэтому средняя энергия частицы равна ![]() .
.
В общем случае у частиц имеются собственные поля, при этом напряжённости и соленоидальные векторы этих полей квадратично входят в соответствующие тензоры энергии-импульса. В связи с этим предполагается, [7] что для энергии полей также справедлива теорема о равнораспределении в том смысле, что энергия системы в равновесии стремится пропорционально распределиться в том числе и между всеми действующими в системе полями. В равновесии можно ожидать, что частные поля, как компоненты общего поля, становятся относительно независимыми друг от друга. В этом случае для каждого поля должны быть справедливы собственные уравнения поля, и уравнения общего поля (4) и (5) разбиваются на комплекты уравнений, отдельные для каждого поля. Все эти уравнения имеют форму, подобную уравнениям Максвелла. [16]
Указанные ниже решения вычислялись при условии, что перекрёстные члены в (7) равны нулю. Это предполагает такую полную независимость частных полей, что не только уравнения частных полей независимы друг от друга, но ещё и то, что энергия общего поля состоит просто из суммы энергий частных полей. Так как частные поля не могут не влиять друг на друга, то эти решения можно рассматривать как первое приближение к реальной картине.
Метрика
За
пределами тел имеется только электромагнитное и гравитационное поле. Только
тензоры энергии-импульса этих полей будут вносить свой вклад в уравнение для
метрики (8), при этом скалярная кривизна
![]() обнуляется. [17]
Метрика вокруг уединённого сферического тела была вычислена в статье. [18]
Для временной компоненты метрического тензора было получено следующее:
обнуляется. [17]
Метрика вокруг уединённого сферического тела была вычислена в статье. [18]
Для временной компоненты метрического тензора было получено следующее:
![]()
где ![]() – расстояние от центра тела до точки, где
определяется метрика,
– расстояние от центра тела до точки, где
определяется метрика, ![]() – энергия гравитационного поля внутри и
снаружи тела,
– энергия гравитационного поля внутри и
снаружи тела, ![]() – энергия электрического поля,
– энергия электрического поля, ![]() ,
, ![]() и
и ![]() – масса, заряд и радиус тела,
– масса, заряд и радиус тела, ![]() – электрическая
постоянная,
– электрическая
постоянная, ![]() –
коэффициенты, подлежащие определению,
–
коэффициенты, подлежащие определению, ![]() – численные коэффициенты порядка единицы, в
случае однородной плотности массы и заряда тела они одинаковы и равны
приблизительно величине 5/3.
– численные коэффициенты порядка единицы, в
случае однородной плотности массы и заряда тела они одинаковы и равны
приблизительно величине 5/3.
В
данном случае оказывается, что метрика зависит как от отношения радиуса тела к
радиус-вектору до точки наблюдения, так и от отношения суммарной энергии полей
к энергии покоя тела.
Компоненты
метрического тензора в веществе массивного тела сферической формы, с учётом
гравитационного и электромагнитных полей, поля ускорений и поля давления, были
найдены в статье. [19] Хотя зависимости компонент
метрического тензора от текущего радиуса внутри и снаружи тела разные, на
поверхности тела соответствующие компоненты должны совпадать друг с другом. Это
позволяет найти часть неизвестных коэффициентов и уточнить компоненты метрики
за пределами тела в следующем виде.
![]()
![]()
где ![]() –
фактор Лоренца движения частиц в центре сферы; величины
–
фактор Лоренца движения частиц в центре сферы; величины ![]() и
и ![]() являются вспомогательными
величинами;
являются вспомогательными
величинами; ![]() –
инвариантная плотность массы частиц вещества внутри сферы;
–
инвариантная плотность массы частиц вещества внутри сферы; ![]() –
инвариантная плотность заряда частиц вещества, движущихся внутри сферы;
–
инвариантная плотность заряда частиц вещества, движущихся внутри сферы; ![]() –
гравитационный потенциал на поверхности сферы с радиусом
–
гравитационный потенциал на поверхности сферы с радиусом ![]() и
гравитационной массой
и
гравитационной массой ![]() ;
; ![]() –
гравитационный потенциал за пределами сферы;
–
гравитационный потенциал за пределами сферы; ![]() –
электрический потенциал на поверхности сферы с электрическим зарядом
сферы
–
электрический потенциал на поверхности сферы с электрическим зарядом
сферы ![]() ;
; ![]() –
электрический потенциал за пределами сферы;
–
электрический потенциал за пределами сферы; ![]() –
потенциал поля давления в центре сферы.
–
потенциал поля давления в центре сферы.
Релятивистская энергия и масса
Энергия
системы частиц с учётом электромагнитного и гравитационного полей, поля
ускорений и поля давления вычислялась в статье. [15] Было показано,
что в системе центра инерции суммарная энергия и импульс всех полей оказываются
равными нулю, а энергия системы формируется лишь из энергии частиц, находящихся
под действием указанных частных полей. Для системы можно ввести пять значений масс:
инертная масса ![]() ;
гравитационная масса
;
гравитационная масса ![]() ; суммарная масса
; суммарная масса ![]() всех частиц тела, разнесённых порознь на
бесконечность; масса
всех частиц тела, разнесённых порознь на
бесконечность; масса ![]() , получаемая путём интегрирования по объёму плотности
, получаемая путём интегрирования по объёму плотности ![]() движущегося внутри системы вещества;
вспомогательная масса
движущегося внутри системы вещества;
вспомогательная масса ![]() , получаемая путём интегрирования по объёму плотности
, получаемая путём интегрирования по объёму плотности ![]() вещества, вычисляемой в сопутствующей для
каждой частицы системе отсчёта. Для данных масс получается соотношение:
вещества, вычисляемой в сопутствующей для
каждой частицы системе отсчёта. Для данных масс получается соотношение:
![]()
Из
равенства ![]() следует, что
допустимым оказывается идеальный сферический коллапс, когда энергия системы не
меняется при сжатии вещества. Кроме этого, гравитационная масса
следует, что
допустимым оказывается идеальный сферический коллапс, когда энергия системы не
меняется при сжатии вещества. Кроме этого, гравитационная масса ![]() оказывается больше, чем масса системы
оказывается больше, чем масса системы ![]() . Это
связано с тем, что частицы внутри системы движутся и их энергия выше, чем если
бы частицы находились неподвижно на бесконечности и не взаимодействовали друг с
другом.
. Это
связано с тем, что частицы внутри системы движутся и их энергия выше, чем если
бы частицы находились неподвижно на бесконечности и не взаимодействовали друг с
другом.
Расчёт
показывает, что энергия электромагнитного поля уменьшает гравитационную массу.
Следовательно, добавление множества зарядов на некоторое тело может привести к
ситуации, когда гравитационная масса тела начнёт уменьшаться, невзирая на
добавочную массу привнесённых зарядов. Это следует из того, что масса зарядов
растёт пропорционально их количеству, а масса-энергия электромагнитного поля
увеличивается квадратично количеству зарядов. Можно подсчитать, что если тело
массой 1 кг и радиусом 1 метр зарядить до потенциала порядка 5 мегавольт, то
это должно уменьшить гравитационную массу тела (без учёта массы добавленных
зарядов) при взвешивании в поле тяжести на ![]() долю массы, что близко к современной точности
измерения массы.
долю массы, что близко к современной точности
измерения массы.
Если учесть более точное соотношение для коэффициентов
полей, для масс получается другое выражение: [20]
![]()
Здесь калибровочная масса
![]() связана с космологической постоянной и
представляет собой массу-энергию частиц вещества в 4-потенциалах полей системы;
инертная масса
связана с космологической постоянной и
представляет собой массу-энергию частиц вещества в 4-потенциалах полей системы;
инертная масса ![]() ;
вспомогательная масса
;
вспомогательная масса ![]() равняется произведению плотности массы частиц
на объём системы; масса
равняется произведению плотности массы частиц
на объём системы; масса ![]() есть сумма инвариантных масс (масс покоя)
частиц системы, равная по величине гравитационной массе
есть сумма инвариантных масс (масс покоя)
частиц системы, равная по величине гравитационной массе ![]() .
.
Вывод о том, что по мере увеличения электрического заряда
масса системы может уменьшаться, остаётся справедливым, но это относится не к
гравитационной массе ![]() , а к инертной массе
, а к инертной массе ![]() системы.
системы.
Энергия
физической системы была найдена в статье, [21] через
скалярные потенциалы ![]() ,
через векторные потенциалы
,
через векторные потенциалы ![]() ,
через тензоры полей
,
через тензоры полей ![]() и
скорости частиц
и
скорости частиц ![]() :
:
![]() ,
через векторные потенциалы полей
,
через векторные потенциалы полей ![]() ,
и через тензоры полей
,
и через тензоры полей ![]() :
:
![]()
![]()
![]()
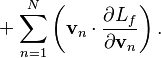
Последний
член в данном выражении описывает вклад в энергию от полей системы. Этот член
зависит от скоростей частиц ![]() ,
при этом всё вещество системы делится на
,
при этом всё вещество системы делится на ![]() частей
так, чтобы каждая часть представляла собой точечную частицу или малый элемент
вещества. Величина
частей
так, чтобы каждая часть представляла собой точечную частицу или малый элемент
вещества. Величина ![]() есть
функция Лагранжа, содержащая тензорные инварианты полей
есть
функция Лагранжа, содержащая тензорные инварианты полей
4-импульс
системы определяется формулой:
![]()
где ![]() обозначает
импульс системы.
обозначает
импульс системы.
Интегральный вектор, проблема 4/3 и теорема Пойнтинга
Проблема
4/3, согласно которой масса поля, находимая через энергию поля, не равна массе
поля, определяемой через поток энергии поля, и проблема энергии нейтрино в
идеальном сферическом коллапсе сверхновой, рассматривались в статье. [10]
Было показано, что в движущемся теле избыток массы-энергии гравитационного и
электромагнитного полей компенсируется недостатком в массе-энергии поля ускорений и поля давления. Результат
достигается путём интегрирования уравнения движения и вычисления сохраняющегося
интегрального вектора системы. Так как этот интегральный вектор должен быть
равен нулю, в отличие от обычного 4-вектора энергии-импульса системы, то это
накладывает ограничения на постоянную ![]() ,
находящуюся в тензоре энергии-импульса поля
ускорений, и на постоянную
,
находящуюся в тензоре энергии-импульса поля
ускорений, и на постоянную ![]() в тензоре
энергии-импульса поля давления. Для этих постоянных в случае массивной
гравитационно-связанной системы из частиц и полей находится соотношение,
связывающее их с гравитационной постоянной и с электрической постоянной:
в тензоре
энергии-импульса поля давления. Для этих постоянных в случае массивной
гравитационно-связанной системы из частиц и полей находится соотношение,
связывающее их с гравитационной постоянной и с электрической постоянной:
![]() ,
,
где ![]() и
и ![]() обозначают заряд и массу системы, а их
отношение в рамках принятых допущений можно трактовать как отношение плотности
заряда к плотности массы.
обозначают заряд и массу системы, а их
отношение в рамках принятых допущений можно трактовать как отношение плотности
заряда к плотности массы.
Решение волнового уравнения для поля ускорений внутри системы приводит к распределению температуры по формуле:
![]()
где ![]() – температура в центре,
– температура в центре, ![]() – масса частицы, в качестве которой
принимается масса протона (для систем, основой которых является водород или
нуклоны в атомных ядрах),
– масса частицы, в качестве которой
принимается масса протона (для систем, основой которых является водород или
нуклоны в атомных ядрах), ![]() – масса системы внутри текущего радиуса
– масса системы внутри текущего радиуса ![]() ,
, ![]() – постоянная Больцмана.
– постоянная Больцмана.
Аналогично, для распределения давления внутри системы получается:
![]()
где ![]() – давление в центре,
– давление в центре, ![]() – плотность массы в сопутствующей частице
вещества системе отсчёта,
– плотность массы в сопутствующей частице
вещества системе отсчёта, ![]() – фактор Лоренца в центре.
– фактор Лоренца в центре.
Данные
формулы хорошо выполняются для самых разных космических объектов, включая
газовые облака и глобулы Бока, Землю, Солнце и нейтронные звёзды. Лишь для
давления в центре Солнца обнаружилось существенное, в 58 раз, расхождение.
Однако, если взять в учёт наличие термоядерных реакций в ядре Солнца, которые
можно описать путём введения поля сильного и поля слабого взаимодействий,
повышенное давление в центре Солнца можно объяснить действием этих полей. [7]
При этом для постоянной ![]() в тензоре
энергии-импульса поля сильного взаимодействия получается оценка:
в тензоре
энергии-импульса поля сильного взаимодействия получается оценка: ![]() ,
то есть то же самое, что для коэффициентов
,
то есть то же самое, что для коэффициентов ![]() и
и ![]() для поля ускорений и поля давления,
соответственно. Во всех случаях скалярные потенциалы частных полей внутри тел
изменяются пропорционально квадрату радиуса, как это имеет место для
гравитационного поля.
для поля ускорений и поля давления,
соответственно. Во всех случаях скалярные потенциалы частных полей внутри тел
изменяются пропорционально квадрату радиуса, как это имеет место для
гравитационного поля.
В статье [14]
проблема 4/3 была объяснена с помощью обобщённой теоремы Пойнтинга. Данная
теорема применяется к 4-тензорам полей, входящих в состав компонент общего
поля. Указанные тензоры состоят из компонент напряжённостей и соленоидальных
векторов соответствующих полей, с помощью которых находятся энергия и импульс
этих полей. В результате получается более точное соотношение между
коэффициентами полей внутри вещества массивных тел: [14] [22]
![]()
позволяющее
делать оценки внутренней температуры, давления и других параметров космических
тел для случая неоднородной плотности.
В силу
теоремы Пойнтинга обнуляется как сумма плотностей энергии всех полей внутри
тела, так и сумма векторов потоков энергии всех полей внутри этого тела. За
пределами тела поток энергии гравитационного или электромагнитного поля точно
компенсирует изменение энергии соответствующего поля в каждом выделенном
объёме. В результате проблема 4/3 исчезает внутри тела, но остаётся для полей,
выходящих за пределы тела. Решение проблемы 4/3 на примере
электромагнитного поля сводится к следующему: требование равенства массы-энергии, связанной с временной
компонентой ![]() тензора энергии-импульса поля, и массы
-энергии потока энергии этого поля в компонентах
тензора энергии-импульса поля, и массы
-энергии потока энергии этого поля в компонентах ![]() тензора, незаконно. Дело в том, что эти
компоненты тензора не составляют 4-вектор и потому не могут содержать одну и ту
же массу-энергию, как это имеет место в 4-импульсе.
тензора, незаконно. Дело в том, что эти
компоненты тензора не составляют 4-вектор и потому не могут содержать одну и ту
же массу-энергию, как это имеет место в 4-импульсе.
Такие же результаты были получены и в статье, [21] в которой вычислялись компоненты интегрального вектора внутри и снаружи движущегося сферического тела.
Диссипация энергии
Одной из компонент общего поля является поле диссипации, которое описывает энергию, импульс и поток энергии, которые связаны с процессами преобразования энергии частных полей в тепловую энергию. В реальном веществе может происходить взаимодействие потоков вещества, движущихся с разными скоростями, под действием внутреннего трения и вязкости. В подобных процессах скорости потоков вещества выравниваются, их кинетическая энергия уменьшается, но растёт тепловая энергия, и суммарная энергия системы не меняется. Оказывается, что если ввести поле диссипации как векторное поле, подобно всем другим частным полям, то при подходящем выборе скалярного потенциала поля диссипации это позволяет получить уравнение Навье-Стокса в гидродинамике и описать движение вязкого сжимаемого вещества. [6]
Если предположить условие локального равновесия и справедливость теоремы о равнораспределении энергии, тогда с достаточной степенью точности становится возможным использовать для каждого частного поля свои собственные уравнения поля. В результате для давления, для которого ранее не были известны уравнения его поля, возникают конкретные волновые уравнения для скалярного и векторного потенциалов поля давления, а также уравнения для напряжённости и соленоидального векторов поля давления. Аналогичные уравнения будут справедливы для поля диссипации, электромагнитного и гравитационного полей, поля ускорений и т.д. Это позволяет замкнуть систему уравнений для движущегося вещества с действующими в этом веществе полями, и сделать эту систему уравнений в принципе разрешимой.
Теорема вириала
Согласно
данной теореме, в каждой стационарной физической системе существует взаимосвязь
между кинетической энергией частиц и энергией, связанной с действующими силами
от всех имеющихся полей, в совокупности составляющих общее поле. В случае,
когда в физической системе учитывается поле давления, поле ускорений частиц,
электромагнитное и гравитационное поля, теорема вириала в релятивистской форме
выражается следующим образом: [23]
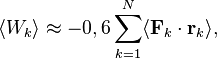
Где ![]() обозначает радиус-вектор
обозначает радиус-вектор ![]() -й
частицы,
-й
частицы, ![]() – сила, действующая на эту частицу, а
величина
– сила, действующая на эту частицу, а
величина ![]() превышает кинетическую энергию частиц
превышает кинетическую энергию частиц ![]() на множитель, равный фактору Лоренца
на множитель, равный фактору Лоренца ![]() частиц в центре системы.
частиц в центре системы.
В слабых полях можно считать,
что ![]() ,
и тогда видно, что в теореме вириала кинетическая энергия связана с энергией
сил в правой части равенства не коэффициентом 0,5 как в классическом случае, а
скорее коэффициентом, близким к 0,6. Отличие от классического случая возникает
за счёт учёта поля давления и поля ускорений частиц внутри системы. Находится
выражение для скалярной вириальной функции
,
и тогда видно, что в теореме вириала кинетическая энергия связана с энергией
сил в правой части равенства не коэффициентом 0,5 как в классическом случае, а
скорее коэффициентом, близким к 0,6. Отличие от классического случая возникает
за счёт учёта поля давления и поля ускорений частиц внутри системы. Находится
выражение для скалярной вириальной функции
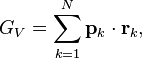
где ![]() есть импульс
есть импульс ![]() -й
частицы, и показывается, что производная от этой функции не равна нулю и должна
рассматриваться как производная Лагранжа. Кроме того, обнаруживается, что в
отличие от выводов классической механики, энергия, связанная с действующими
силами от всех имеющихся полей и входящая в правую часть теоремы вириала, не
равна потенциальной энергии системы. [24]
-й
частицы, и показывается, что производная от этой функции не равна нулю и должна
рассматриваться как производная Лагранжа. Кроме того, обнаруживается, что в
отличие от выводов классической механики, энергия, связанная с действующими
силами от всех имеющихся полей и входящая в правую часть теоремы вириала, не
равна потенциальной энергии системы. [24]
Анализ интегральной теоремы обобщённого вириала позволяет
найти на основе теории поля формулу для среднеквадратичной скорости типичных
частиц системы, не используя понятия температуры: [25]
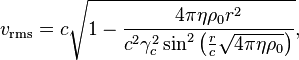
где ![]() есть скорость света,
есть скорость света, ![]() – постоянная поля ускорений,
– постоянная поля ускорений, ![]() – плотность массы частиц,
– плотность массы частиц, ![]() – текущий радиус.
– текущий радиус.
Показывается связь данной теоремы с космологической
постоянной, характеризующей рассматриваемую физическую систему. Объясняется
различие между кинетической энергией, и энергией движения, значение которой
равняется половине суммы лагранжиана и гамильтониана.
Энергия связи макроскопических тел
Релятивистская
энергия, полная энергия, энергия связи, энергия полей, энергия давления и
потенциальная энергия системы из частиц и четырёх полей – компонент общего
поля, вычисляются в релятивистской однородной модели, [24] и затем
сравниваются с кинетической энергией частиц и с суммарной энергией
гравитационного и электромагнитного поля за пределами системы. Другим
результатом является то, что инертная масса системы получается меньше, чем
гравитационная масса, которая равна суммарной инвариантной массе частиц,
составляющих систему. Также доказывается, что по мере образования всё более
массивных релятивистских однородных систем средняя плотность этих систем
уменьшается по сравнению со средней плотностью слагающих эти системы частиц или
тел.
Модель даёт возможность оценить скорость ![]() частиц в центре сферы, соответствующий фактор
Лоренца
частиц в центре сферы, соответствующий фактор
Лоренца ![]() , скалярный потенциал
, скалярный потенциал ![]() поля давления, найти связь между
коэффициентами полей, выразить зависимости скалярной кривизны и космологической
постоянной в веществе как функции от параметров типичных частиц и потенциалов
полей. [17] При этом сравнение космологических
постоянных внутри протона, нейтронной звезды и в наблюдаемой Вселенной
позволяет объяснить проблему космологической постоянной, возникающую в
Lambda-CDM модели.
поля давления, найти связь между
коэффициентами полей, выразить зависимости скалярной кривизны и космологической
постоянной в веществе как функции от параметров типичных частиц и потенциалов
полей. [17] При этом сравнение космологических
постоянных внутри протона, нейтронной звезды и в наблюдаемой Вселенной
позволяет объяснить проблему космологической постоянной, возникающую в
Lambda-CDM модели.
Сущность общего поля
Общее поле предполагается основным источником действующих сил, энергии и импульса, а также основой для вычисления метрики системы с точки зрения не квантовой классической теории поля.
Из всех полей, которые объединяет общее поле, два поля, электромагнитное и гравитационное поля, действуют на расстоянии, а остальные поля действуют локально в месте расположения того или иного элемента вещества. Собственный векторный потенциал любого поля для одной частицы пропорционален скалярному потенциалу этого поля и скорости движения частицы, если векторный потенциал этой частицы равен нулю в сопутствующей частице системе отсчёта. Для электромагнитного и гравитационного полей в системе со множеством частиц известен принцип суперпозиции, по которому скалярный потенциал в произвольной точке является суммой скалярных потенциалов всех частиц, и то же самое предполагается для векторного потенциала. Ввиду различия правил суммирования векторов и скаляров, векторный потенциал системы перестаёт зависеть от скалярного потенциала системы частиц. Такая же картина должна быть и для других полей. Например, давление вблизи частицы зависит не только от скалярного потенциала поля давления в сопутствующей системе отсчёта и от скорости частицы, но и от суммарного давления со стороны других частиц системы.
Скалярные потенциалы частных полей пропорциональны энергии, появляющейся в системе в ходе того или иного взаимодействия, в расчёте на единицу массы (заряда) вещества, и имеют размерность квадрата скорости. Векторные потенциалы частных полей имеют размерность скорости и позволяют учесть дополнительную энергию, появляющуюся за счёт движения. Так как 4-потенциал частного поля состоит из скалярного и векторного потенциалов, то сумма 4-потенциалов частных полей даёт 4-потенциал общего поля, который описывает полную энергию всех взаимодействий в системе из частиц и полей. Именно поэтому общее поле существует до тех пор, пока существует хотя бы одна из его компонент в виде какого-либо частного поля. С философской точки зрения, существование только одного частного поля невозможно – всегда должны быть ещё и другие поля. Например, если есть частица, движение которой описывается полем ускорений, то у этой частицы должно быть как минимум ещё гравитационное поле, а внутри частицы ещё и полный набор собственных внутренних полей.
Наиболее
естественный способ описания возникновения общего поля предоставляет теория гравитации Фатио-Лесажа. Эта теория
даёт ясный физический механизм возникновения гравитационной силы, [26]
[27] [28] [29] как следствие воздействия на
тела вездесущих потоков гравитонов в виде мельчайших частиц наподобие нейтрино
или фотонов. Этот же механизм позволяет объяснить и электромагнитное
взаимодействие, если допустить наличие в потоках гравитонов праонов – мельчайших заряженных частиц. [3]
[30] Праоны и нейтральные частицы в виде квантов полей образуют
вакуумное поле, содержащееся в электрогравитационном
вакууме. Потоки частиц вакуумного поля пронизывают все тела и осуществляют
электромагнитное и гравитационное взаимодействие посредством поля даже между
удалёнными друг от друга телами. Тела могут также оказывать друг на друга прямое
механическое действие, что может быть представлено через поле давления.
Неизбежным следствием действия этих полей является торможение быстрых частиц и
тел в окружающей среде, описываемое посредством поля диссипации. Наконец, поле ускорений вводится для кинематического
описания движения частиц и тел, действующих на них сил, энергии и импульса
движения.
Для тел
сферической формы хаотически движущиеся частицы их вещества могут
характеризоваться некоторой средней радиальной скоростью и перпендикулярной ей
средней тангенциальной скоростью, значения которых зависят от текущего радиуса.
Можно считать, что градиент радиальной скорости приводит к радиальному
ускорению, описываемому с помощью поля давления. Тангенциальная скорость частиц
также порождает радиальное ускорение за счёт центростремительной силы, что
может быть учтено полем ускорений. Указанные радиальные ускорения с добавкой от
ускорения от электрических сил в заряженном веществе противостоят ускорению от
гравитационных сил, сжимающих вещество массивных космических тел.
В
результате, общее поле может быть представлено как поле, в котором нейтральные
и заряженные тела, находящиеся в потоках нейтральных и заряженных частиц
вакуумного поля, обмениваются друг с другом и с вакуумным полем энергией и
импульсом. Энергию и импульс общего поля можно связать с энергией и импульсом,
которые приобретает вакуумное поле при взаимодействии с веществом, а для учёта
энергии и импульса системы необходимо ещё добавить энергию и импульс вещества
от его взаимодействия с вакуумным полем.
В модели кварковых квазичастиц подчёркивается, что кварки являются не настоящими частицами, а квазичастицами. В связи с этим предполагается, что сильное взаимодействие может быть сведено к сильной гравитации, действующей на уровне атомов и элементарных частиц, с заменой гравитационной постоянной на постоянную сильной гравитации. [3] [4] На основе сильной гравитации и поля кручения обосновывается гравитационная модель сильного взаимодействия. Одним из следствий этого является то, что гравитационное и электромагнитное поля представляются фундаментальными полями, действующими на разных уровням материи посредством полевых квантов с различной величиной своего спина и энергии, и с различной проникающей способностью в веществе.
Указанный подход позволил вычислить радиус протона в самосогласованной модели и объяснить длину волны де Бройля. [31] Что касается слабого взаимодействия, то с точки зрения теории бесконечной вложенности материи оно сводится к процессам трансформации вещества, находящегося под действием фундаментальных полей, с учётом действия сильной гравитации. Точно так же, поле давления и поле диссипации могли бы в принципе свестись к фундаментальным полям, если были бы известны все детали межатомного и межмолекулярного взаимодействия. Ввиду трудностей с такой детализацией, приходится приписывать существование своих собственных 4-потенциалов у поля давления, поля диссипации энергии, поля сильного взаимодействия и поля слабого взаимодействия, и аппроксимировать действие этих полей в веществе с помощью этих 4-потенциалов.
По аналогии с электромагнитным полем, все поля, входящие как компоненты в общее поле, рассматриваются как векторные поля. Для таких полей доказана интегральная теорема энергии поля. [32] Данная теорема является аналогом теоремы вириала и описывает связи между различными компонентами энергии полей.
В статье [33] концепция общего поля была проанализирована
вновь и определена основная действующая компонента электрогравитационного
вакуума в виде потоков заряженных частиц типа праонов. Предполагается, что данная компонента
ответственна за электромагнитное и за гравитационное взаимодействия, а также за
действие других полей внутри тел. На основе
такого подхода удалось объяснить принцип действия двигателя космического
корабля, который для своего движения использует энергию космического
вакуума. [34]
См. также
- Теория
всего
- Теории
Великого объединения
- Фундаментальные
взаимодействия
- Ковариантная теория гравитации
- Метрическая
теория относительности
- Поле ускорений
- Поле давления
- Поле диссипации
- Теория гравитации Лесажа
- Сильная гравитация
- Постоянная сильной гравитации
- Гравитационная модель сильного
взаимодействия
- Модель кварковых квазичастиц
- Предел
массы-энергии поля
- Уравнение
векторного поля
Ссылки
- Fedosin
S.G. The procedure of finding the stress-energy tensor and vector field
equations of any form. Advanced Studies in
Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101;
статья на русском языке: Процедура для
нахождения тензора энергии-импульса и уравнений векторного поля любого
вида.
- Fedosin
S.G. The Principle of Least Action in Covariant Theory of Gravitation.
Hadronic
Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804; статья на русском
языке: Принцип наименьшего действия в
ковариантной теории гравитации.
- а б в Федосин С. Г. Физические теории и бесконечная вложенность
материи, Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN
978-5-9901951-1-0.
- а б Федосин С.
Г. Физика и философия подобия от преонов
до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93,
Библ. 377 назв. ISBN 5-8131-0012-1.
- Fedosin
S.G. About the cosmological
constant, acceleration field, pressure field and energy.
Jordan
Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; статья на русском
языке: О космологической постоянной, поле
ускорения, поле давления и об энергии.
- а
б
в
г Fedosin S.G. Four-Dimensional Equation of Motion for Viscous
Compressible and Charged Fluid with Regard to the Acceleration Field,
Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No.
1, pp. 13‒24 (2015). http://dx.doi.org/10.5541/ijot.5000034003;
статья на русском языке: Четырёхмерное
уравнение движения вязкого сжимаемого вещества с учётом поля ускорений,
поля давления и поля диссипации.
- а б
в г Fedosin S.G. The Concept of the General Force Vector
Field. OALib Journal, Vol. 3, pp.
1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459;
статья на русском языке: Концепция общего
силового векторного поля.
- а
б Fedosin S.G. Two components of the macroscopic general field.
Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages
(2017). http://dx.doi.org/10.1142/S2424942417500025; статья
на
русском
языке: Две компоненты макроскопического общего поля.
- Fedosin
S.G. The Hamiltonian in Covariant Theory of Gravitation.
Advances in
Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023;
статья на русском языке: Гамильтониан в
ковариантной теории гравитации.
- а б в
Fedosin S.G. The Integral Energy-Momentum 4-Vector and
Analysis of 4/3 Problem Based on the Pressure Field and Acceleration
Field. American Journal
of Modern Physics.
Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12 ;
статья на русском языке: Интегральный
4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и
поля ускорений.
- Fedosin S.G. The electromagnetic field in the
relativistic uniform model. International Journal of Pure and Applied
Sciences, Vol. 4, Issue. 2, pp. 110-116 (2018). http://dx.doi.org/10.29132/ijpas.430614.
// Электромагнитное поле в
релятивистской однородной модели.
- Fedosin
S.G. The gravitational field in the
relativistic uniform model within the framework of the covariant theory of
gravitation. 5th Ulyanovsk International School-Seminar
“Problems of Theoretical and Observational Cosmology” (UISS 2016), Ulyanovsk, Russia, September
19-30, 2016, Abstracts, p. 23, ISBN 978-5-86045-872-7.
- Fedosin S.G. The Gravitational
Field in the Relativistic Uniform Model within the Framework of the
Covariant Theory of Gravitation. International Letters of
Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39;
статья на русском языке: Гравитационное
поле в релятивистской однородной модели в рамках ковариантной теории
гравитации.
- а
б
в
Fedosin S.G. The generalized Poynting theorem for the general field
and solution of the 4/3 problem. International Frontier Science Letters,
Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19. //
Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.
- а
б Fedosin S.G. Relativistic Energy and Mass in
the Weak Field Limit. Jordan Journal
of Physics. Vol. 8, No. 1, pp.
1‒16 (2015). http://dx.doi.org/10.5281/zenodo.889210; статья на русском
языке: Релятивистская энергия и масса в
пределе слабого поля.
- Fedosin
S.G. Lagrangian formalism in the theory of relativistic vector fields.
International Journal of Modern Physics A, Vol. 40, No. 02, 2450163
(2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских
векторных полей.
- а б Fedosin S.G. Energy and metric gauging in the covariant theory
of gravitation. Aksaray University Journal of Science and Engineering,
Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
// Калибровка энергии и метрики в
ковариантной теории гравитации.
- Fedosin
S.G. The Metric Outside a Fixed Charged Body in the Covariant Theory of
Gravitation. International Frontier Science Letters, ISSN: 2349 —
4484, Vol. 1, No. I, pp. 41-46 (2014). http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41 ;
статья на русском языке: Метрика за пределами
неподвижного заряженного тела в ковариантной теории гравитации.
- Fedosin
S.G. The relativistic uniform model: the metric of the covariant theory of
gravitation inside a body. St. Petersburg Polytechnical State University
Journal. Physics and Mathematics, Vol. 14, No. 3, pp.168-184 (2021). http://dx.doi.org/10.18721/JPM.14313.
// О метрике ковариантной теории
гравитации внутри тела в релятивистской однородной модели.
- Fedosin S.G. The Mass Hierarchy in the
Relativistic Uniform System.
Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp.
73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
// Иерархия масс в
релятивистской однородной системе.
- а б Fedosin S.G. What should we
understand by the four-momentum of physical system? Physica Scripta, Vol.
99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.
// Что мы должны понимать под
4-импульсом физической системы?
- Fedosin
S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model.
Canadian
Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593;
статья на русском языке: Оценка
физических параметров планет и звёзд в модели гравитационного равновесия.
- Fedosin
S.G. The virial theorem and
the kinetic energy of particles of a macroscopic system in the general
field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue
2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8; статья на
русском языке: Теорема вириала и
кинетическая энергия частиц макроскопической системы в концепции общего
поля.
- а
б
Fedosin S.G. The binding energy and the total energy of a
macroscopic body in the relativistic uniform model. Middle East
Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
// Энергия связи и полная энергия
макроскопического тела в релятивистской однородной модели.
- Fedosin S.G. The
integral theorem of generalized virial in the relativistic uniform model.
Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638
(2019). https://dx.doi.org/10.1007/s00161-018-0715-x. Интегральная теорема обобщённого вириала в
релятивистской однородной модели.
- Fedosin
S.G. Model of Gravitational Interaction in the Concept of Gravitons.
Journal of
Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009). http://dx.doi.org/10.5281/zenodo.890886; статья на русском
языке: Модель гравитационного
взаимодействия в концепции гравитонов.
- Michelini
M. A flux of Micro-quanta explains
Relativistic Mechanics and the Gravitational Interaction. Apeiron
Journal, Vol.14, pp. 65-94 (2007).
- Fedosin
S.G. The graviton field as the source of mass and gravitational force in
the modernized Le Sage’s model. Physical Science International Journal, ISSN:
2348‒0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197;
статья на русском языке: Поле гравитонов
как источник гравитационной силы и массы в модернизированной модели Лесажа.
- Fedosin
S.G. The Force Vacuum Field as an Alternative
to the Ether and Quantum Vacuum.
WSEAS Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN:
1991-8747 / 2224-3429, Volume 10, Art. #3, pp. 31-38 (2015). http://dx.doi.org/10.5281/zenodo.888979; статья на русском
языке: Силовое вакуумное поле как
альтернатива эфиру и квантовому вакууму.
- Fedosin S.G. The charged component of the
vacuum field as the source of electric force in the modernized Le Sage’s
model. Journal of Fundamental and Applied
Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18,
https://dx.doi.org/10.5281/zenodo.845357.
// Заряженная компонента вакуумного поля
как источник электрической силы в модернизированной модели Лесажа.
- Fedosin
S.G. The radius of the proton in the self-consistent model.
Hadronic
Journal, Vol. 35, No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451; статья на русском
языке: Радиус протона в самосогласованной
модели.
- Fedosin S.G. The Integral Theorem of the Field Energy.
Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. //
Интегральная теорема энергии поля.
- Fedosin S.G. On the structure of the force field in electro gravitational vacuum. Canadian Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp. 5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206. // О структуре силового поля в электрогравитационном вакууме.
- Fedosin S.G. The Principle of Operation of an Engine That Draws Energy from the Electrogravitational Vacuum. Jordan Journal of Physics, Vol. 17, No. 1, pp. 87-95 (2024). https://doi.org/10.47011/17.1.8. // Принцип действия двигателя, черпающего энергию из электрогравитационного вакуума.
|
Фундаментальные
взаимодействия (в квантовой теории) |
|
Сильное
взаимодействие • Электромагнитное взаимодействие • Слабое взаимодействие
• Гравитация |
