In English

Тензор энергии-импульса поля давления

Из проекта Викизнание

Тензор энергии-импульса поля давления — симметричный четырёхмерный тензор второй валентности (ранга), описывающий плотность энергии и плотность потока энергии поля давления в веществе. Данный тензор в ковариантной теории гравитации входит в уравнение для определения метрики наравне с тензором энергии-импульса гравитационного поля, с тензором энергии-импульса поля ускорений, с тензором энергии-импульса поля диссипации, и с аналогичным тензором электромагнитного поля. Ковариантная производная тензора энергии-импульса поля давления задаёт плотность силы давления, действующей в веществе.

Тензор энергии-импульса поля давления является релятивистским обобщением трёхмерного тензора напряжений, используемого в механике сплошных сред. В отличие от тензора напряжений, который применяется обычно для описания относительных напряжений, появляющихся при деформациях тел, тензор энергии-импульса поля давления описывает любые внутренние напряжения, в том числе и в отсутствие деформации тел от внешних воздействий.

2.1 Определение
2.2 Компоненты тензора энергии-импульса поля давления
2.3 Cила давления и уравнения поля давления
2.4 Уравнение для метрики
2.5 Уравнение движения
2.6 Законы сохранения

3 См. также
4 Ссылки
5 Внешние ссылки

Механика сплошных сред

Существование различных вариантов тензора энергии-импульса давления показывает отсутствие какого-то однозначного определения этого тензора. Кроме 4-скорости, плотности и давления, в данный тензор часто добавляют функцию с заданными свойствами такими, чтобы тензор мог описывать энергию и напряжения в веществе. Произвол выбора подобной функции связан с тем, что когда полагают давление простой скалярной функцией, то возникает необходимость восполнить векторные свойства сил давления какой-то дополнительной функцией.

Примеры тензоров

Для вещества, находящегося в равновесии при однородном давлении, простейший тензор энергии-импульса давления в метрике (+ – – –) записывается так:

$~ P^{ik} = \frac{p} {c^2 }u^i u^k - g^{ik}p ,$

где – давление, – скорость света, – 4-скорость, $~ g^{ik}$ – метрический тензор.

Ввиду своей простоты тензор в таком виде часто используется не только в механике, но и в общей теории относительности.

Фок вводит в рассмотрение плотность упругой энергии на единицу массы $~ \Pi$ и добавляет эту величину в тензор энергии-импульса давления: ^[1]

$~ P^{ik} = \frac{p+ \rho^{*} \Pi } {c^2 }u^i u^k - g^{ik}p ,$

здесь $~ \rho^{*}$ обозначает ту плотность массы, которая не зависит от давления, и связана с полной инвариантной плотностью массы $~ \rho_0$ соотношением:

$~ \rho^{*}= \frac{ \rho_0 } {1+\Pi /c^2 }.$

Вместо этого Федосин использовал функцию сжатия : ^[2]

$~ P^{ik} = \frac{p} {c^2 }u^i u^k + (L-p) g^{ik}.$

Известны и другие формы тензора энергии-импульса давления, отличающиеся друг от друга способом введения в тензор некоторой дополнительной к давлению скалярной функции. ^[3] ^[4] ^[5]

Описание движения и метрики

Стандартный подход предполагает вначале определение тензора энергии-импульса системы $~ T^{ik}= \phi^{ik}+ P^{ik}+ W^{ik},$ где $~ \phi^{ik}= \rho_0 u^i u^k$ представляет тензор энергии-импульса вещества, а $~ W^{ik}$ является тензором энергии-импульса электромагнитного поля. После этого уравнение движения с учётом давления и других полей следует из равенства нулю ковариантной производной тензора энергии-импульса системы: $~ - \nabla_k T^{ik}=0.$ При этом в общей теории относительности (ОТО) учёт гравитационного поля в уравнении движения осуществляется через зависимость компонент метрического тензора от координат и времени.

Тензор $~ T^{ik}$ используется в ОТО также для нахождения метрики из уравнения Гильберта-Эйнштейна :

$~ R_{ik} - \frac{1} {2 }g_{ik}R + g_{ik} \Lambda = \frac{8 \pi G } { c^4} T_{ik},$

где $~ R_{ik}={R^n}_{ink}$ – тензор Риччи, $~ R=R_{ik}g^{ik}$ – скалярная кривизна, – гравитационная постоянная.

Таким образом, тензор энергии-импульса давления изменяет метрику внутри тел.

Ковариантная теория гравитации

Определение

В отличие от механики сплошной среды, в ковариантной теории гравитации (КТГ) поле давления считается не скалярным, а 4-векторным полем, состоящим из скалярной и 3-векторной компонент. Поэтому в КТГ тензор энергии-импульса поля давления определяется через тензор поля давления $~f_{ik}$ и метрический тензор $~ g^{ik}$ из принципа наименьшего действия: ^[6]

$~ P^{ik} = \frac{c^2} {4 \pi \sigma } \left( - g^{im} f_{nm} f^{nk}+ \frac {1} {4} g^{ik}f_{mr}f^{mr}\right) ,$

где $~ \sigma$ – постоянная, имеющая своё собственное значение в каждой задаче. То, что $~ \sigma$ не определена однозначно, является следствием того факта, что давление внутри тел может быть вызвано действием любых причин и сил как внутреннего, так и внешнего характера. Поле давления рассматривается как компонента общего поля.^[7]

Компоненты тензора энергии-импульса поля давления

В пределе слабого поля, когда метрика пространства-времени переходит в метрику пространства Минковского специальной теории относительности, метрический тензор $~ g^{ik}$ переходит в тензор $~ \eta^{ik}$ , состоящий из чисел 0, 1, –1. В этом случае вид тензора энергии-импульса поля давления существенно упрощается и его можно выразить через компоненты тензора поля давления, то есть через напряжённость поля давления $~\mathbf{ C}$ и соленоидальный вектор $~\mathbf{I}$ :

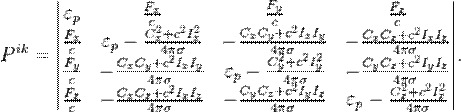
Временные компоненты тензора обозначают:

1) объёмная плотность энергии поля давления

$~ P^{00} = \varepsilon_p = \frac{1}{8 \pi \sigma }\left(C^2+ c^2 I^2 \right).$

2) вектор плотности потока энергии поля давления:

$~\mathbf{F} = \frac{ c^2 }{4 \pi \sigma }[\mathbf{C}\times \mathbf{I}].$

Компоненты вектора $~\mathbf{F}$ входят в соответствующие компоненты тензора $P 01, P 02, P 03$ , при этом вследствие симметрии тензора по индексам $P 01 = P 10, P 02 = P 20, P 03 = P 30$ .

3) Пространственные компоненты тензора образуют 3 x 3 подматрицу, являющуюся 3-мерным тензором напряжений поля давления, взятым со знаком минус. Тензор напряжений можно записать в следующем виде:

$~ \sigma^{p q} = \frac {1}{4 \pi \sigma } \left( C^p C^q + c^2 I^p I^q - \frac {1}{2} \delta^{pq} (C^2 + c^2 I^2 ) \right) ,$

где $p, q$ $= 1,2,3,$ компоненты $C 1 = C x,$ $C 2 = C y,$ $C 3 = C z,$ $I 1 = I x,$ $I 2 = I y,$ $I 3 = I z,$ символ Кронекера $δ pq$ равен 1 при $p = q,$ и равен нулю при $p \not=q.$

Представленный тензор напряжений является конкретным выражением тензора напряжений Коши.

Трёхмерная дивергенция тензора напряжений поля давления связывает плотность силы давления и скорость изменения плотности потока энергии поля давления:

$~ \partial_q \sigma^{p q} = f^p +\frac {1}{c^2} \frac{ \partial F^p}{\partial t},$

где обозначают компоненты трёхмерной плотности силы давления, – компоненты вектора плотности потока энергии поля давления.

Сила давления и уравнения поля давления

Из принципа наименьшего действия следует, что 4-вектор плотности силы давления $~ f^\alpha$ может быть найден через тензор энергии-импульса поля давления, либо через произведение тензора поля давления и массового 4-тока:

$~f^{\alpha }=-\nabla _{\beta }P^{{\alpha \beta }}={f^{\alpha }}_{{i}}J^{i}.\qquad (1)$

Соотношение (1) тесно связано с уравнениями поля давления:

$~ \nabla_n f_{ik} + \nabla_i f_{kn} + \nabla_k f_{ni}=0,$

$~\nabla_k f^{ik} = -\frac {4 \pi \sigma }{c^2} J^i .$

В рамках специальной теории относительности согласно (1) для компонент плотности 4-силы давления можно записать:

$~ f^\alpha = (\frac {\mathbf{C} \cdot \mathbf{J} }{c}, \mathbf{f} ),$

где $~ \mathbf{f}= \rho \mathbf{C} + [\mathbf{J} \times \mathbf{I} ]$ – 3-вектор плотности силы давления, $~\rho$ – плотность движущегося вещества, $~\mathbf{J} =\rho \mathbf{v}$ – 3-вектор плотности массового тока, $~\mathbf{v}$ – 3-вектор скорости движения элемента вещества.

В пространстве Минковского уравнения поля давления преобразуются в 4 уравнения для напряжённости поля давления $~\mathbf{ C}$ и соленоидального вектора $~\mathbf{I}$ :

$~\nabla \cdot \mathbf{ C} = 4 \pi \sigma \rho,$

$~\nabla \times \mathbf{ I} = \frac {1 }{c^2}\frac{\partial \mathbf{ C}}{\partial t}+\frac {4 \pi \sigma \rho \mathbf{ v}}{c^2},$

$~\nabla \cdot \mathbf{ I} = 0,$

$~\nabla \times \mathbf{ C} = - \frac{\partial \mathbf{ I}}{\partial t}.$

Уравнение для метрики

В ковариантной теории гравитации тензор энергии-импульса поля давления в соответствии с принципами метрической теории относительности является одним из тензоров, определяющих метрику внутри тел посредством уравнения для метрики: ^[8]

$~ R_{ik} - \frac{1} {4 }g_{ik}R = \frac{8 \pi G \beta }{ c^4} \left( B_{ik}+ P_{ik}+ U_{ik}+ W_{ik} \right),$

где $~ \beta$ – коэффициент, подлежащий определению, $~ B_{ik}$ , $~ P_{ik}$ , $~ U_{ik}$ и $~ W_{ik}$ – соответственно тензоры плотности энергии-импульса поля ускорений, поля давления, гравитационного и электромагнитного полей.

Уравнение движения

Уравнение движения точечной частицы внутри или за пределами вещества может быть представлено в тензорном виде, с участием тензора энергии-импульса давления $P ik$ или тензора поля давления $f nk$ :

$~ - \nabla_k \left( B^{ik}+ U^{ik} +W^{ik}+ P^{ik} \right) = g^{in}\left(u_{nk} J^k + \Phi_{nk} J^k + F_{nk} j^k + f_{nk} J^k \right) =0. \qquad (2)$

где $~ u_{nk}$ – тензор ускорений, $~ \Phi_{nk}$ – тензор гравитационного поля, $~F_{nk}$ – тензор электромагнитного поля, $~j^k = \rho_{0q} u^k$ – зарядовый 4-ток, $~\rho_{0q}$ – плотность электрического заряда элемента вещества в системе его покоя, – 4-скорость.

Временная компонента уравнения (2) при описывает изменение энергии, а пространственная компонента при связывает ускорение с плотностями действующих сил.

Законы сохранения

Временную компоненту в (2) можно рассматривать как локальный закон сохранения энергии и потока энергии. В пределе специальной теории относительности, когда ковариантная производная становится 4-градиентом, а символы Кристоффеля обращаются в нуль, этот закон сохранения приобретает простой вид: ^[9] ^[10]

$~\nabla \cdot ({\mathbf {K}}+{\mathbf {H}}+{\mathbf {P}}+{\mathbf {F}})=-{\frac {\partial (B^{{00}}+U^{{00}}+W^{{00}}+P^{{00}})}{\partial t}},$

где $~ \mathbf{K}$ – вектор плотности потока энергии поля ускорений, $~ \mathbf{H}$ – вектор Хевисайда, $~ \mathbf{P}$ – вектор Пойнтинга, $~ \mathbf{F}$ – вектор плотности потока энергии поля давления.

Согласно данному закону, работа поля по ускорению масс и зарядов компенсируется работой вещества по созданию поля. В результате изменение во времени суммарной энергии в некотором объёме возможно только за счёт втекания в этот объём потоков энергии.

Интегральная форма закона сохранения энергии и потока энергии получается путём интегрирования уравнения (2) по всему 4-объёму, чтобы учесть энергию и поток энергии гравитационного и электромагнитного полей, простирающихся далеко за пределы рассматриваемой физической системы. При интегрировании (2) применяется формула Гаусса-Остроградского, которая заменяет интегрирование дивергенции суммы тензоров по 4-объёму на интегрирование суммы временных компонент тензоров по 3-объёму. В результате в лоренцевых координатах получается интегральный вектор, равный нулю:

$~{\mathbb {Q}}^{i}=\int {\left(B^{{i0}}+U^{{i0}}+W^{{i0}}+P^{{i0}}\right)dV}.$

Равенство нулю интегрального вектора позволяет объяснить проблему 4/3, согласно которой масса-энергия поля в потоке энергии поля движущейся системы в 4/3 больше, чем в энергии поля неподвижной системы. С другой стороны, согласно ^[10] обобщённая теорема Пойнтинга и интегральный вектор должны рассматриваться по разному в веществе и за его пределами. В результате возникновение проблемы 4/3 связывается с тем, что временные компоненты тензоров энергии-импульса не образуют 4-векторы и потому принципиально не могут задавать одну и ту же массу в энергии и в импульсе полей. ^[11]

См. также

Поле давления
Тензор энергии-импульса гравитационного поля
Тензор энергии-импульса электромагнитного поля
Тензор энергии-импульса поля ускорений
Тензор энергии-импульса поля диссипации
Тензор поля давления
Тензор напряжений
Общее поле
Поле диссипации
Поле ускорений

Ссылки

1. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. – 568 с.

2. Федосин С.Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.

3. Herglotz G. // Ann. d. Phys. 1911, Bd 36, S. 493.

4. Ignatowsky W.V. // Phys. Ztschr. 1911, Bd 12, S. 441.

5. Lamla E. // Berl. Diss., 1911; Ann. d. Phys. 1912, Bd 37, S. 772.

6. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; статья на русском языке: О космологической постоянной, поле ускорения, поле давления и об энергии.

7. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025. // Две компоненты макроскопического общего поля.

8. Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских векторных полей.

9. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. http://dx.doi.org/10.11648/j.ajmp.20140304.12 ; статья на русском языке: Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

10. ^а ^б Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19. // Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.

11. Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?

Внешние ссылки

Pressure stress-energy tensor

Источник: http://sergf.ru/ps.htm

На список страниц