In English

Тензор энергии-импульса поля ускорений

Из проекта Викизнание

 

Тензор энергии-импульса поля ускорений — симметричный четырёхмерный тензор второго ранга, описывающий плотность энергии и плотность потока энергии поля ускорений в веществе. Данный тензор, а также тензор энергии-импульса гравитационного поля, тензор энергии-импульса электромагнитного поля, тензор энергии-импульса поля диссипации и тензор энергии-импульса поля давления входят в уравнение для определения метрики в ковариантной теории гравитации. Ковариантная производная тензора энергии-импульса поля ускорений позволяет вычислить плотность 4-силы, действующей в веществе.

Содержание

Ковариантная теория гравитации

Определение

В ковариантной теории гравитации (КТГ) поле ускорений считается не скалярным, а 4-векторным полем, 4-потенциал которого состоит из скалярной и 3-векторной компонент. В КТГ тензор энергии-импульса поля ускорений был определён Федосиным через тензор ускорений  ~u_{{ik}}  и метрический тензор  ~g^{{ik}}  из принципа наименьшего действия: [1]

~B^{{ik}}={\frac {c^{2}}{4\pi \eta }}\left(-g^{{im}}u_{{nm}}u^{{nk}}+{\frac {1}{4}}g^{{ik}}u_{{mr}}u^{{mr}}\right),

где ~\eta  – постоянная поля ускорения, определяемая через фундаментальные постоянные и физические параметры системы. Поле ускорений рассматривается как компонента общего поля.

Компоненты тензора энергии-импульса поля ускорений

Так как тензор ускорений состоит из компонент напряжённости поля ускорений  ~{\mathbf {S}}  и соленоидального вектора ускорений  ~{\mathbf {N}}, то тензор энергии-импульса поля ускорений можно выразить через эти компоненты. В пределе специальной теории относительности метрический тензор перестаёт зависеть от координат и времени и в этом случае тензор энергии-импульса поля ускорений приобретает наиболее простой вид:

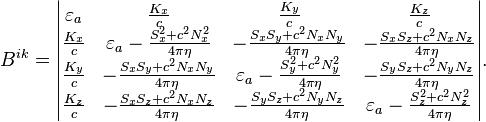
~B^{{ik}}={\begin{vmatrix}\varepsilon _{a}&{\frac {K_{x}}{c}}&{\frac {K_{y}}{c}}&{\frac {K_{z}}{c}}\\{\frac {K_{x}}{c}}&\varepsilon _{a}-{\frac {S_{x}^{2}+c^{2}N_{x}^{2}}{4\pi \eta }}&-{\frac {S_{x}S_{y}+c^{2}N_{x}N_{y}}{4\pi \eta }}&-{\frac {S_{x}S_{z}+c^{2}N_{x}N_{z}}{4\pi \eta }}\\{\frac {K_{y}}{c}}&-{\frac {S_{x}S_{y}+c^{2}N_{x}N_{y}}{4\pi \eta }}&\varepsilon _{a}-{\frac {S_{y}^{2}+c^{2}N_{y}^{2}}{4\pi \eta }}&-{\frac {S_{y}S_{z}+c^{2}N_{y}N_{z}}{4\pi \eta }}\\{\frac {K_{z}}{c}}&-{\frac {S_{x}S_{z}+c^{2}N_{x}N_{z}}{4\pi \eta }}&-{\frac {S_{y}S_{z}+c^{2}N_{y}N_{z}}{4\pi \eta }}&\varepsilon _{a}-{\frac {S_{z}^{2}+c^{2}N_{z}^{2}}{4\pi \eta }}\end{vmatrix}}.

Временные компоненты тензора обозначают:

1) объёмная плотность энергии поля ускорений

~B^{{00}}=\varepsilon _{a}={\frac {1}{8\pi \eta }}\left(S^{2}+c^{2}N^{2}\right).

2) вектор плотности потока энергии поля ускорений:

~{\mathbf {K}}={\frac {c^{2}}{4\pi \eta }}[{\mathbf {S}}\times {\mathbf {N}}].

Компоненты вектора ~{\mathbf {K}}  входят в соответствующие компоненты тензора B^{{01}}, B^{{02}}, B^{{03}}.

Вследствие симметрии тензора по индексам  B^{{01}}=B^{{10}},B^{{02}}=B^{{20}},B^{{03}}=B^{{30}} 

3) Пространственные компоненты тензора образуют 3 x 3 подматрицу, являющуюся 3-мерным тензором напряжений поля ускорений, взятым со знаком минус. Данный 3-мерный тензор можно записать в следующем виде:

~\sigma ^{{pq}}={\frac {1}{4\pi \eta }}\left(S^{p}S^{q}+c^{2}N^{p}N^{q}-{\frac {1}{2}}\delta ^{{pq}}(S^{2}+c^{2}N^{2})\right),

где  p,q=1,2,3,  компоненты  S^{1}=S_{x},  S^{2}=S_{y},  S^{3}=S_{z},  N^{1}=N_{x},  N^{2}=N_{y},  N^{3}=N_{z}, символ Кронекера  \delta ^{{pq}}  равен 1 при  p=q,  и равен нулю при  p\not =q.

Трёхмерная дивергенция тензора напряжений поля ускорений связывает плотность силы и скорость изменения плотности потока энергии поля ускорений:

~\partial _{q}\sigma ^{{pq}}=-f^{p}+{\frac {1}{c^{2}}}{\frac {\partial K^{p}}{\partial t}},

где  ~f^{p}  обозначают компоненты трёхмерной плотности силы ускорения, ~K^{p} – компоненты вектора плотности потока энергии поля ускорений.

Плотность 4-силы и уравнения поля

Из принципа наименьшего действия следует, что 4-вектор плотности силы  ~f_{\alpha }  может быть найден через тензор энергии-импульса поля ускорений, либо через произведение тензора поля ускорений и массового 4-тока: [2]

~f_{\alpha }=\nabla _{\beta }{B_{\alpha }}^{\beta }=-u_{{\alpha k}}J^{k}.\qquad (1)

Уравнения поля ускорений записываются следующим образом:

~\nabla _{n}u_{{ik}}+\nabla _{i}u_{{kn}}+\nabla _{k}u_{{ni}}=0,

 

~\nabla _{k}u^{{ik}}=-{\frac {4\pi \eta }{c^{2}}}J^{i}.

В рамках специальной теории относительности согласно (1) для компонент плотности 4-силы можно записать:

~f_{\alpha }=(-{\frac {{\mathbf {S}}\cdot {\mathbf {J}}}{c}},-{\mathbf {f}}),

где  ~{\mathbf {f}}=-\rho {\mathbf {S}}-[{\mathbf {J}}\times {\mathbf {N}}]  – 3-вектор плотности силы, ~\rho   – плотность движущегося вещества, ~{\mathbf {J}}=\rho {\mathbf {v}} – 3-вектор плотности массового тока, ~{\mathbf {v}} – 3-вектор скорости движения элемента вещества.

В пространстве Минковского уравнения поля ускорений превращаются в четыре уравнения для вектора напряжённости поля ускорений  ~{\mathbf {S}}  и соленоидального вектора ускорений  ~{\mathbf {N}} :

~\nabla \cdot {\mathbf {S}}=4\pi \eta \rho ,

 

~\nabla \times {\mathbf {N}}={\frac {1}{c^{2}}}{\frac {\partial {\mathbf {S}}}{\partial t}}+{\frac {4\pi \eta \rho {\mathbf {v}}}{c^{2}}},

 

~\nabla \cdot {\mathbf {N}}=0,

 

~\nabla \times {\mathbf {S}}=-{\frac {\partial {\mathbf {N}}}{\partial t}}.

Уравнение для метрики

В ковариантной теории гравитации тензор энергии-импульса поля ускорений в соответствии с принципами метрической теории относительности является одним из тензоров, определяющих метрику внутри тел посредством уравнения для метрики:

~R_{{ik}}-{\frac {1}{4}}g_{{ik}}R={\frac {8\pi G\beta }{c^{4}}}\left(B_{{ik}}+P_{{ik}}+U_{{ik}}+W_{{ik}}\right),

где ~\beta  – коэффициент, подлежащий определению, ~B_{{ik}}, ~P_{{ik}}, ~U_{{ik}}и ~W_{{ik}} – соответственно тензоры плотности энергии-импульса поля ускорений, поля давления, гравитационного и электромагнитного полей, ~G – гравитационная постоянная.

Уравнение движения

Уравнение движения точечной частицы внутри или за пределами вещества может быть представлено в тензорном виде, с участием тензора энергии-импульса поля ускорений  B^{{ik}} или тензора ускорений u_{{nk}}:

~-\nabla _{k}\left(B^{{ik}}+U^{{ik}}+W^{{ik}}+P^{{ik}}\right)=g^{{in}}\left(u_{{nk}}J^{k}+\Phi _{{nk}}J^{k}+F_{{nk}}j^{k}+f_{{nk}}J^{k}\right)=0.\qquad (2)

где  ~\Phi _{{nk}} – тензор гравитационного поля, ~F_{{nk}} – тензор электромагнитного поля, ~f_{{nk}} – тензор поля давления, ~j^{k}=\rho _{{0q}}u^{k} – зарядовый 4-ток, ~\rho _{{0q}} – плотность электрического заряда элемента вещества в системе его покоя, ~u^{k} – 4-скорость.

Учтём теперь, что  ~J^{k}=\rho _{{0}}u^{k}  есть массовый 4-ток, а тензор ускорений определяется через 4-потенциал в виде  ~u_{{nk}}=\nabla _{n}U_{k}-\nabla _{k}U_{n}.  Это даёт следующее: [3]

~\nabla _{\beta }{B_{n}}^{\beta }=-u_{{nk}}J^{k}=-\rho _{{0}}u^{k}(\nabla _{n}U_{k}-\nabla _{k}U_{n})=\rho _{{0}}{\frac {DU_{n}}{D\tau }}-\rho _{{0}}u^{k}\nabla _{n}U_{k}.\qquad (3)

Здесь использован оператор производной по собственному времени  ~u^{k}\nabla _{k}={\frac {D}{D\tau }} ,  где ~D – символ 4-дифференциала в искривлённом пространстве-времени, ~\tau  – собственное время, ~\rho _{0}  есть плотность массы в сопутствующей системе отсчёта.

С учётом этого уравнение движения (2) приобретает вид: [4] [5]

Временная компонента данного уравнения при  ~n=0  описывает скорость изменения скалярного потенциала поля ускорений, а пространственная компонента при  ~n=1{,}2{,}3  связывает скорость изменения векторного потенциала поля ускорений с плотностями действующих сил. В правой части уравнения присутствуют 4-скорость  ~u_{n}  и 4-ускорение  ~A_{n}, которые могут быть найдены, если известны тензоры всех полей.

Законы сохранения

При индексе  ~i=0  в (2), то есть для временной компоненты уравнения, в пределе специальной теории относительности из равенства нулю левой части (2) следует:

~\nabla \cdot ({\mathbf {K}}+{\mathbf {H}}+{\mathbf {P}}+{\mathbf {F}})=-{\frac {\partial (B^{{00}}+U^{{00}}+W^{{00}}+P^{{00}})}{\partial t}},

где  ~{\mathbf {K}}  – вектор плотности потока энергии поля ускорений, ~{\mathbf {H}} – вектор Хевисайда, ~{\mathbf {P}} – вектор Пойнтинга, ~{\mathbf {F}} – вектор плотности потока энергии поля давления.

Это соотношение можно рассматривать как локальный закон сохранения энергии и потока энергии всех четырёх полей. [6]

Интегральная форма закона сохранения энергии и потока энергии получается путём интегрирования уравнения (2) по всему 4-объёму. При интегрировании (2) применяется формула Гаусса-Остроградского, которая заменяет интегрирование дивергенции суммы тензоров по 4-объёму на интегрирование суммы временных компонент тензоров по 3-объёму. В результате в лоренцевых координатах получается интегральный вектор, равный нулю: [7]

~{\mathbb {Q}}^{i}=\int {\left(B^{{i0}}+U^{{i0}}+W^{{i0}}+P^{{i0}}\right)dV}.

Равенство нулю интегрального вектора позволяет объяснить проблему 4/3, согласно которой масса-энергия поля в потоке энергии поля движущейся системы в 4/3 больше, чем в энергии поля неподвижной системы. С другой стороны, согласно [6] обобщённая теорема Пойнтинга и интегральный вектор должны рассматриваться по разному в веществе и за его пределами. В результате возникновение проблемы 4/3 связывается с тем, что временные компоненты тензоров энергии-импульса не образуют 4-векторы и потому принципиально не могут задавать одну и ту же массу в энергии и в потоке энергии полей. В [8] показывается, что интегральный вектор не даёт возможности найти 4-импульс физической системы. Однако энергия и импульс, являющиеся компонентами 4-импульса, могут быть найдены в ковариантном виде. В таком случае состояние физической системы определяется через 4-импульс центра импульсов системы.

Общая теория относительности

В общей теории относительности (ОТО), тензор энергии-импульса поля ускорений не используется. Вместо него применяется так называемый тензор энергии-импульса вещества, имеющий в простейшем случае следующий вид:  ~\phi _{{n\beta }}=\rho _{0}u_{n}u_{\beta } . В ОТО тензор  ~\phi _{{n\beta }}  подставляется в уравнение для метрики, а его ковариантная производная даёт следующее:

~\nabla ^{\beta }\phi _{{n\beta }}=\nabla ^{\beta }(\rho _{0}u_{n}u_{\beta })=u_{n}\nabla ^{\beta }J_{\beta }+\rho _{0}u_{\beta }\nabla ^{\beta }u_{n}.

Если предположить, что выполняется уравнение непрерывности в виде  ~\nabla ^{\beta }J_{\beta }=0,  то с учётом оператора производной по собственному времени ковариантная производная тензора  ~\phi _{{n\beta }}  даёт произведение плотности на 4-ускорение, то есть плотность 4-силы:

~\nabla ^{\beta }\phi _{{n\beta }}=\rho _{0}u_{\beta }\nabla ^{\beta }u_{n}=\rho _{0}u^{\beta }\nabla _{\beta }u_{n}=\rho _{0}{\frac {Du_{n}}{D\tau }}.\qquad (5)

 

Из сравнения (5) и (4) следует, что тензор  ~\phi _{{n\beta }}=\rho _{0}u_{n}u_{\beta }  в общей теории относительности используется как эквивалент тензора энергии-импульса поля ускорений  ~B_{{nk}}  ковариантной теории гравитации.

См. также

Ссылки

1.      Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30 (2016); статья на русском языке: О космологической постоянной, поле ускорения, поле давления и об энергии.

2.      Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских векторных полей.

3.      Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в теории релятивистских векторных полей.

4.      Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003; статья на русском языке: Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.

5.      Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017).  http://dx.doi.org/10.1142/S2424942417500025; статья на русском языке: Две компоненты макроскопического общего поля.

6.      а б Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19. // Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.

7.      Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). https://dx.doi.org/10.11648/j.ajmp.20140304.12; статья на русском языке: Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

8.      Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?

Внешние ссылки

 

Источник: http://sergf.ru/as.htm

На список страниц