In English

Тензор поля давления

Из проекта Викизнание

Тензор поля давления — антисимметричный тензор, описывающий поле давления и состоящий из шести компонент. Компоненты тензора являются в то же время компонентами двух трёхмерных векторов – напряжённости поля давления, и соленоидального вектора давления. С помощью тензора поля давления определяются тензор энергии-импульса поля давления, уравнения поля давления и сила давления в веществе. Поле давления является компонентой общего поля.

Определение

Выражение для тензора поля давления можно найти в работах Федосина, ^[1] где тензор определяется через 4-ротор:

$f_{\mu \nu} = \nabla_\mu \pi_\nu - \nabla_\nu \pi_\mu = \frac{\partial \pi_\nu}{\partial x^\mu} - \frac{\partial \pi_\mu}{\partial x^\nu}.\qquad\qquad (1)$

Здесь 4-потенциал поля давления $~ \pi_\mu$ определяется по формуле:

$~\pi_\mu = \left( \frac {\wp }{ c}, -\mathbf{\Pi } \right),$

где $~\wp$ – скалярный потенциал, $~ \mathbf{\Pi }$ – векторный потенциал поля давления, – скорость света.

Выражение для компонент

С помощью (1) находятся вектор напряжённости поля давления и соленоидальный вектор давления:

$~ C_i= c (\partial_0 \pi_i -\partial_i \pi_0),$

$~ I_k= \partial_i \pi_j -\partial_j \pi_i ,$

и это же в векторной записи:

$~\mathbf{C}= -\nabla \wp - \frac{\partial \mathbf{\Pi }} {\partial t},$

$~\mathbf{I }= \nabla \times \mathbf{\Pi }.$

Тензор поля давления состоит из компонент данных векторов:

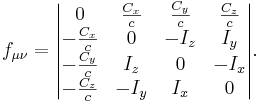
$~ f_{\mu \nu}= \begin{vmatrix} 0 & \frac {C_x}{ c} & \frac {C_y}{ c} & \frac {C_z}{ c} \\ -\frac {C_x}{ c} & 0 & - I_{z} & I_{y} \\ -\frac {C_y}{ c} & I_{z} & 0 & -I_{x} \\ -\frac {C_z}{ c}& -I_{y} & I_{x} & 0 \end{vmatrix}.$

Переход к тензору поля давления с контравариантными индексами осуществляется путём двойного умножения на метрический тензор:

$~ f^{\alpha \beta}= g^{\alpha \nu} g^{\mu \beta} f_{\mu \nu}.$

В рамках специальной теории относительности этот тензор имеет вид:

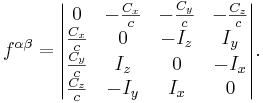
$~ f^{\alpha \beta}= \begin{vmatrix} 0 &- \frac {C_{x}}{ c} & -\frac {C_{y}}{ c} & -\frac {C_{z}}{ c} \\ \frac {C_{x}}{ c} & 0 & - I_{z} & I_{y} \\ \frac {C_{y}}{ c}& I_{z} & 0 & -I_{x} \\ \frac {C_{z}}{ c}& -I_{y} & I_{x} & 0 \end{vmatrix}.$

Для преобразования компонент тензора поля давления из одной инерциальной системы отсчёта в другую нужно учитывать правило преобразования тензоров. Если система отсчёта K’ движется с произвольной постоянной скоростью $~\mathbf {V}$ относительно неподвижной системы отсчёта K, а оси систем координат параллельны друг другу, напряжённость поля давления и соленоидальный вектор давления преобразуются так:

$\mathbf {C}^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {C}) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {C}-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {C}) + [\mathbf {V} \times \mathbf {I }] \right),$

$\mathbf {I }^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {I }) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {I }-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {I }) - \frac {1}{ c^2} [\mathbf {V} \times \mathbf {C}] \right).$

Свойства тензора

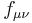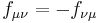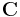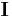$~ f_{\mu \nu}$ является антисимметричным тензором 2-го ранга, отсюда следует условие $~ f_{\mu \nu}= -f_{\nu \mu}$ . Три из шести независимых компонент тензора поля давления связаны с компонентами вектора напряжённости поля давления $~\mathbf{ C }$ , а другие три – с компонентами соленоидального вектора давления $~\mathbf{I }$ . 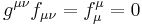Ввиду антисимметричности такой инвариант, как свёртка тензора с метрическим тензором, обращается в нуль: $~ g^{\mu \nu} f_{\mu \nu}= f^{\mu}_\mu =0$ .
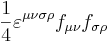Свёртка тензора с самим собой $f μν f μν$ является инвариантом, а свёртка произведения тензоров с символом Леви-Чивиты в виде $\frac {1}{4} \varepsilon^{\mu \nu \sigma \rho} f_{\mu \nu} f_{\sigma \rho}$ является псевдоскалярным инвариантом. Указанные инварианты в специальной теории относительности выражаются так:

$f_{\mu \nu} f^{\mu \nu} = -\frac {2}{c^2} (C^2- c^2 I^2) = inv,$

$\frac {1}{4} \varepsilon^{\mu \nu \sigma \rho}f_{\mu \nu} f_{\sigma \rho} = - \frac {2}{ c } \left( \mathbf C \cdot \mathbf {I} \right) = inv.$

Детерминант тензора также является лоренцевским инвариантом:

$\det \left( f_{\mu \nu} \right) = \frac{4}{c^2} \left(\mathbf C \cdot \mathbf {I} \right)^{2}.$

Поле давления

Через тензор поля давления записываются уравнения поля давления:

$\nabla_\sigma f_{\mu \nu}+\nabla_\mu f_{\nu \sigma}+\nabla_\nu f_{\sigma \mu}=\frac{\partial f_{\mu \nu}}{\partial x^\sigma} + \frac{\partial f_{\nu \sigma}}{\partial x^\mu} + \frac{\partial f_{\sigma \mu}}{\partial x^\nu} = 0. \qquad\qquad (2)$

$~ \nabla_\nu f^{\mu \nu} = - \frac{4 \pi \sigma }{c^2} J^\mu, \qquad\qquad (3)$

где $J μ = ρ 0 u μ$ есть массовый 4-ток, $ρ 0$ – плотность массы в сопутствующей системе отсчёта, $u μ$ – 4-скорость движения элемента вещества, $~ \sigma$ – постоянная, определяемая в каждой задаче.

Вместо (2) можно использовать выражение:

$~ \varepsilon^{\mu \nu \sigma \rho}\frac{\partial f_{\mu \nu}}{\partial x^\sigma} = 0 .$

Равенство (2) выполняется тождественно, что доказывается подстановкой в него определения для тензора поля давления согласно (1). Если подставить в (2) компоненты тензора $f μν$ , можно получить два векторных уравнения:

$~ \nabla \times \mathbf{C} = - \frac{\partial \mathbf{I} } {\partial t} , \qquad\qquad (4)$

$~ \nabla \cdot \mathbf{I} = 0 . \qquad\qquad (5)$

Согласно (5), соленоидальный вектор давления не имеет источников, так как его дивергенция равна нулю. Из (4) следует, что изменение во времени соленоидального вектора давления приводит к появлению ротора напряжённости поля давления.

Уравнение (3) связывает поле давления с его источником в виде массового 4-тока. В пространстве Минковского специальной теории относительности вид уравнения упрощается и становится следующим:

$~ \nabla \cdot \mathbf{C} = 4 \pi \sigma \rho,$

$~ \nabla \times \mathbf{I} = \frac{1}{c^2} \left( 4 \pi \sigma \mathbf{J} + \frac{\partial \mathbf{C}} {\partial t} \right),$

где $~ \rho$ – плотность движущейся массы, $~ \mathbf{J}$ – плотность тока массы.

Согласно первому из этих уравнений, напряжённость поля давления имеет источник в виде плотности вещества, а по второму уравнению ток массы либо изменение во времени вектора напряжённости поля давления порождают круговое поле соленоидального вектора давления.

Из (3) и (1) можно получить следующее: ^[1]

$~ R_{ \mu \alpha } f^{\mu \alpha }= \frac {4 \pi \sigma }{c^2} \nabla_{\alpha}J^{\alpha}.$

Уравнение непрерывности для массового 4-тока $~\nabla _{{\alpha }}J^{{\alpha }}=0$ является калибровочным условием, которое используется для получения уравнения поля (3) из принципа наименьшего действия. Следовательно, свёртка тензора поля давления и тензора Риччи должна равняться нулю: $~R_{{\mu \alpha }}f^{{\mu \alpha }}=0$ . В пространстве Минковского тензор Риччи $~R_{{\mu \alpha }}$ равен нулю, ковариантная производная превращается в частную производную, и уравнение непрерывности становится таким:

$~\partial_{\alpha } J^\alpha = \frac {\partial \rho } {\partial t}+ \nabla \cdot \mathbf{J} =0.$

Волновое уравнение для тензора поля давления выглядит следующим образом: ^[2]

$~\nabla ^{\sigma }\nabla _{\sigma }f_{{\mu \nu }}={\frac {4\pi \sigma }{c^{2}}}\nabla _{\mu }J_{\nu }-{\frac {4\pi \sigma }{c^{2}}}\nabla _{\nu }J_{\mu }+f_{{\nu \rho }}{R^{\rho }}_{\mu }-f_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}f^{{\eta \lambda }}.$

Использование в ковариантной теории гравитации

Действие и Лагранжиан

Полный Лагранжиан для вещества в гравитационном и электромагнитном полях включает в себя тензор поля давления и содержится в функции действия: ^[1]

$~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}D_\mu J^\mu + \frac {c}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu} -\frac {1}{c}A_\mu j^\mu - \frac {c \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu} -$

$~-{\frac {1}{c}}U_{\mu }J^{\mu }-{\frac {c}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}-{\frac {1}{c}}\pi _{\mu }J^{\mu }-{\frac {c}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,$

где – функция Лагранжа или лагранжиан, – дифференциал времени используемой системы отсчёта, – некоторый коэффициент, – скалярная кривизна, $~\Lambda$ – космологическая константа, характеризующая плотность энергии рассматриваемой системы в целом, и потому являющаяся функцией системы, – скорость света, как мера скорости распространения электромагнитного и гравитационного взаимодействий, $~ D_\mu$ – гравитационный 4-потенциал, – гравитационная постоянная, $~ \Phi_{ \mu\nu}$ – тензор гравитационного поля, $~ A_\mu$ – электромагнитный 4-потенциал, $~ j^\mu$ – электрический 4-ток, $~\varepsilon_0$ – электрическая постоянная, $~ F_{ \mu\nu}$ – тензор электромагнитного поля, $~U_{\mu }$ – 4-потенциал поля ускорений, $~ \eta$ и $~ \sigma$ – коэффициенты поля ускорений и поля давления, соответственно, $~ u_{ \mu\nu}$ – тензор ускорений, $~ \pi_\mu$ – 4-потенциал поля давления, $~ f_{ \mu\nu}$ – тензор поля давления, $~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3$ – инвариантный 4-объём, выражаемый через дифференциал временной координаты , через произведение дифференциалов пространственных координат, и через квадратный корень $~\sqrt {-g}$ из детерминанта метрического тензора, взятого с отрицательным знаком.

Варьирование функции действия по 4-координатам даёт уравнение движения элемента вещества в гравитационном и электромагнитном полях и в поле давления: ^[2]

$~-u_{{\beta \sigma }}\rho _{{0}}u^{\sigma }=\rho _{0}{\frac {dU_{\beta }}{d\tau }}-\rho _{0}u^{\sigma }\partial _{\beta }U_{\sigma }=\Phi _{{\beta \sigma }}\rho _{0}u^{\sigma }+F_{{\beta \sigma }}\rho _{{0q}}u^{\sigma }+f_{{\beta \sigma }}\rho _{0}u^{\sigma },$

здесь первый член в правой части есть плотность гравитационной силы, выраженная с помощью тензора гравитационного поля, второй член задаёт электромагнитную силу Лоренца для плотности заряда $~ \rho_{0q}$ , измеряемой в сопутствующей системе отсчёта, а последний член определяет силу давления.

Варьирование функции действия по 4-потенциалу поля давления приводит к уравнению поля давления (3).

Тензор энергии-импульса поля давления

С помощью тензора поля давления в ковариантной теории гравитации строится тензор энергии-импульса поля давления:

$~ P^{ik} = \frac{c^2} {4 \pi \sigma }\left( -g^{im} f_{n m} f^{n k}+ \frac{1} {4} g^{ik} f_{m r} f^{m r}\right)$ .

Ковариантная производная от тензора энергии-импульса поля давления задаёт плотность 4-силы давления:

$~f^{\alpha }=-\nabla _{\beta }P^{{\alpha \beta }}={f^{\alpha }}_{{k}}J^{k}.$

Обобщённая скорость и Гамильтониан

Ковариантный 4-вектор обобщённой скорости определяется выражением:

$~s_{{\mu }}=U_{{\mu }}+D_{{\mu }}+{\frac {\rho _{{0q}}}{\rho _{0}}}A_{{\mu }}+\pi _{{\mu }}.$

С учётом обобщённой скорости Гамильтониан содержит в себе тензор поля давления и имеет вид:

$~H = \int {( s_0 J^0 - \frac {c^2}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu}+ \frac {c^2 \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu }+ \frac {c^2 }{16 \pi \eta } u_{ \mu\nu} u^{ \mu\nu}+ \frac {c^2 }{16 \pi \sigma } f_{ \mu\nu} f^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},$