In English

Инвариантная энергия

Из проекта Викизнание

Инвариантная энергия произвольной системы есть положительная величина, состоящая из всех видов энергии системы, и равная релятивистской энергии, измеренной неподвижным относительно центра импульсов системы наблюдателем. В состав инвариантной энергии как правило входят энергия покоя вещества; потенциальная энергия собственных электромагнитных и гравитационных полей, связанных с системой; внутренняя энергия частиц системы; энергия системы во внешних полях; энергия излучения, взаимодействующего с системой. Инвариантная энергия частицы ~E_0  равна её энергии покоя и в силу принципа эквивалентности массы и энергии связана с инерциальной инвариантной массой  ~M  частицы соотношением:

~E_0= Mc^2,

где  ~c – скорость света.

Порядок вычисления инвариантной энергии через различные виды энергии системы определяется принципом суммирования энергий.

Оглавление

  • 1 Связь с другими физическими переменными
    • 1.1 Одна частица
    • 1.2 Система частиц

o    1.3 Массивное тело

·                      1.3.1 Общая теория относительности

·                      1.3.2 Ковариантная теория гравитации

·         2 Ссылки

  • 3 См. также
  • 4 Внешние ссылки

Связь с другими физическими переменными

Одна частица

В рамках специальной теории относительности инвариантная энергия точечной частицы может быть вычислена либо через её релятивистскую энергию ~E и импульс ~ \mathbf {p}, либо через релятивистскую энергию и скорость ~v :

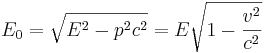~E_0= \sqrt {E^2-p^2 c^2}=E \sqrt {1-\frac {v^2}{c^2}}.

Для фотона справедливо соотношение ~ E=p c, так что инвариантная энергия фотона равна нулю.

В четырёхмерном формализме в пространстве Минковского энергия  ~E_0  может быть вычислена через 4-импульс  ~ p^{\mu}=M u^{\mu}  частицы:

~E_0= c \sqrt { \eta_{\mu \nu} p^{\mu} p^{\nu}}= Mc \sqrt {u_{\mu} u^{\mu}}= Mc^2,

где  ~\eta_{\mu \nu}  есть метрический тензор пространства Минковского,  ~ u^\mu = \left(\gamma c, \gamma {\mathbf {v}}\right)  – 4-скорость,   ~ \gamma = \frac{1}{\sqrt{1-(\frac{v}{c})^2}}  – фактор Лоренца.

В результате 4-импульс может быть представлен через инвариантную энергию: [1]

~p^{\mu }={\frac {E_{0}u^{\mu }}{c^{2}}}=\left({\frac {\gamma E_{0}}{c}},\gamma M{{\mathbf {v}}}\right)=\left({\frac {E}{c}},{\mathbf {p}}\right),

где ~\mathbf {p} – 3-вектор релятивистского импульса.

В искривлённом пространстве-времени с метрическим тензором  ~ g_{\mu \nu}  инвариантная энергия частицы находится так:

~E_0= c \sqrt { g_{\mu \nu} p^{\mu} p^{\nu}}= Mc \sqrt { g_{\mu \nu} u^{\mu} u^{\nu}}.

Если учесть определение 4-скорости:  ~ u^{\mu} = \frac {dx^{\mu} }{d\tau},  где  ~ dx^{\mu}  есть 4-вектор сдвига, ~ d\tau – дифференциал собственного времени, а также определение интервала:  ~ ds = \sqrt { g_{\mu \nu} dx^{\mu} dx^{\nu} }= c d\tau,  то снова получается равенство: ~E_0= Mc^2.

Система частиц

В физике элементарных частиц часто рассматривается взаимодействие нескольких частиц, их слияния и распады с образованием новых частиц. Сохранение суммы 4-импульсов свободных частиц до и после реакции приводит к законам сохранения энергии и импульса рассматриваемой системы частиц. Инвариантная энергия ~E_{0c} системы частиц вычисляется как их полная релятивистская энергия в системе отсчёта, в которой центр импульсов системы частиц неподвижен. При этом ~E_{0c} может отличаться от суммы инвариантных энергий частиц системы, поскольку вклад в ~E_{0c} делают не только энергии покоя частиц, но и кинетические энергии частиц и их потенциальная энергия. [2] Если наблюдать частицы до или после взаимодействия на больших расстояниях друг от друга, когда их взаимной потенциальной энергией можно пренебречь, инвариантная энергия системы определяется соотношением:

~E_{0c}= \sqrt {E_c^2 - p_c^2 c^2},

где ~E_c =\sum_i E_i – сумма релятивистских энергий частиц системы, ~\mathbf {p}_c =\sum_i \mathbf {p}_i – векторная сумма импульсов частиц.

Массивное тело

Общая теория относительности

При определении инвариантной энергии массивного тела в общей теории относительности (ОТО) возникает проблема с вкладом энергии гравитационного поля, [3] поскольку тензор энергии-импульса гравитационного поля однозначно не определён, а вместо него используется псевдотензор [1]. В случае асимптотически плоского пространства-времени на бесконечности для оценки инвариантной энергии может быть применено приближение АДМ массы-энергии тела, [4] смотри также [2]. Для стационарной метрики пространства-времени определяется масса-энергия Комара. [5] [3] Существуют и другие подходы к определению массы-энергии, например, энергия Бонди, [6] и энергия Хокинга [4].

В приближении слабого поля инвариантная энергия неподвижного тела в ОТО оценивается следующим образом: [7]

~E_{0}= Mc^2=m_b c^2 + E_k - \frac {6G m^2_b}{5a}+ \frac {3 q^2_b}{20 \pi \varepsilon_0 a}+E_p,

где масса ~ m_b  и заряд ~ q_b тела получаются путём интегрирования соответствующей плотности по объёму, ~ E_k – энергия движения частиц внутри тела, ~ G – гравитационная постоянная, ~ a – радиус тела, ~ \varepsilon_0 – электрическая постоянная, ~ E_p – упругая энергия.

Для масс получается соотношение:

~ M= m_g < m_b < m',

где инертная масса системы ~ M равна гравитационной массе ~ m_g, масса ~ m' обозначает суммарную массу частиц, из которых составлено тело.

Ковариантная теория гравитации

В ковариантной теории гравитации (КТГ) при вычислении инвариантной энергии учитывается разбиение энергии на 2 основные части – на компоненты энергии самих полей и на компоненты, связанные с энергией частиц в этих полях. Подсчёт показывает, что сумма компонент энергии поля ускорений, поля давления, гравитационного и электромагнитных полей, для тела сферической формы равна нулю. [8] 

Остаётся сумма энергий частиц в четырёх полях, которая в итоге равна:

~E_{{0}}=Mc^{2}\approx m_{b}c^{2}\gamma _{s}-{\frac {3Gm_{b}^{2}}{10a}}+{\frac {3q_{b}^{2}}{40\pi \varepsilon _{0}a}}+m_{b}\wp _{s},

где ~\gamma _{s}  есть фактор Лоренца частиц, а ~\wp _{s}  – скалярный потенциал поля давления вблизи поверхности системы.

Соотношение для масс выглядит следующим образом:  ~m'=M<m_{b}=m_{g}. При этом инертная масса системы ~M получается равной суммарной массе частиц ~m', масса ~m_{b}  равна гравитационной массе ~m_{g}, а превышение ~m_{b}  над ~M  происходит за счёт того, что частицы внутри тела двигаются и находятся под давлением в гравитационном и электромагнитном полях.

Более точное выражение для инвариантной энергии представлено в следующей статье: [9]

~E_{{0}}=Mc^{2}\approx m_{b}c^{2}\gamma _{s}-{\frac {Gm_{b}^{2}}{2a}}+{\frac {q_{b}^{2}}{8\pi \varepsilon _{0}a}}+m_{b}\wp _{s}.

Для случая релятивистской однородной системы инвариантную энергию можно выразить так: [10] [11]

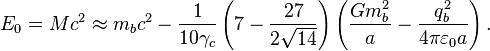
~E_{{0}}=Mc^{2}\approx m_{b}c^{2}-{\frac {1}{10\gamma _{c}}}\left(7-{\frac {27}{2{\sqrt {14}}}}\right)\left({\frac {Gm_{b}^{2}}{a}}-{\frac {q_{b}^{2}}{4\pi \varepsilon _{0}a}}\right).

Это приводит к изменению соотношения для масс:

~m'<M<m<m_{b}=m_{g}.

Здесь калибровочная масса ~m' связана с космологической постоянной и представляет собой массу-энергию частиц вещества в 4-потенциалах полей системы; ~Mесть инерциальная масса системы; вспомогательная масса  ~m равняется произведению плотности массы частиц на объём вещества системы; масса  ~m_{b}  есть сумма инвариантных масс (масс покоя) частиц системы, равная по величине гравитационной массе ~m_{g}  системы.

В лоренц-инвариантной теории гравитации (ЛИТГ), в которую переходит КТГ в приближении слабого поля и при постоянной скорости движения, для инвариантной энергии остаётся справедливой формула:

~ E_{0}= \sqrt {E^2-p^2 c^2},

где ~E – релятивистская энергия движущегося тела с учётом вклада энергии гравитационного и электромагнитного поля, а также энергии поля ускорений и поля давления; ~p – суммарный импульс системы в виде тела и его полей.

Указанные формулы остаются в силе и на уровне атомов с тем отличием, что обычная гравитация заменяется на сильную гравитацию .

В ковариантной теории гравитации с учётом принципа наименьшего действия показывается, что гравитационная масса ~ m_g системы увеличивается за счёт вклада массы-энергии гравитационного поля и уменьшается за счёт вклада электромагнитной массы-энергии. Это является следствием того, что в ЛИТГ и в КТГ точно определён тензор энергии-импульса гравитационного поля, являющийся одним из источников для определения метрики, энергии и уравнений движения вещества и поля. Также определены ковариантным способом тензор энергии-импульса поля ускорений, тензор энергии-импульса поля диссипации и тензор энергии-импульса поля давления.

Такие векторные поля, как гравитационное и электромагнитное поля, поле ускорений, поле давления, поле диссипации, поля сильного и слабого взаимодействий являются компонентами общего поля. Это приводит к тому, что инвариантная энергия системы из частиц и полей может быть вычислена как интеграл по объёму в системе центра импульсов: [12]

 

 ~E = \int {( s_0 J^0 + \frac {c^2 }{16 \pi \varpi } s_{ \mu\nu} s^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},

 

где  ~ s_0    и  ~ J^0   обозначают временные компоненты 4-потенциала  ~ s_{\mu }   общего поля и массового 4-тока  ~ J^{\mu } , соответственно,  ~ s_{ \mu\nu}   – тензор общего поля.

В общем случае энергия системы с учётом четырёх векторных полей вычисляется по формуле: [13]

 

~E={\frac {1}{c}}\int \operatorname {{\big [}}\rho _{{0q}}\varphi +\rho _{0}\psi +\rho _{0}\vartheta +\rho _{0}\wp -{\mathbf v}\cdot {\frac {\partial }{\partial {\mathbf v}}}\left(\rho _{{0q}}\varphi +\rho _{0}\psi +\rho _{0}\vartheta +\rho _{0}\wp \right)+

~+v^{2}{\frac {\partial }{\partial {\mathbf v}}}\left(\rho _{{0q}}{\mathbf A}+\rho _{0}{\mathbf D}+\rho _{0}{\mathbf U}+\rho _{0}{\mathbf \Pi }\right)\operatorname {{\big ]}}u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+

~+\int \left({\frac {1}{4\mu _{0}}}F_{{\mu \nu }}F^{{\mu \nu }}-{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}+{\frac {c^{2}}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}+{\frac {c^{2}}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}+

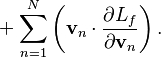
~+\sum _{{n=1}}^{N}\left({\mathbf v}_{n}\cdot {\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right).

 

Здесь  ~\varphi ,\psi ,\vartheta ,\wp   есть скалярные потенциалы электромагнитного и гравитационного полей, поля ускорений и поля давления, соответственно;  ~{\mathbf A},{\mathbf D},{\mathbf U},{\mathbf \Pi }  обозначают векторные потенциалы полей;  ~F_{{\mu \nu }},\Phi _{{\mu \nu }},u_{{\mu \nu }},f_{{\mu \nu }}  есть тензоры этих полей;  ~L_{f}  есть та часть функции Лагранжа, которая связана с тензорными инвариантами;  ~{\mathbf v}_{n}  обозначает скорость частиц системы.

В случае, когда все величины в представленной формуле для энергии вычисляются в системе отсчёта, связанной с центром импульсов системы, получается инвариантная энергия.

Ссылки

  1. McGlinn, William D. Introduction to relativity. — JHU Press, 2004. — С. 43. — ISBN 0-801-87047-X, Extract of page 43
  2. Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
  3. Misner, Charles W.; Kip. S. Thorne & John A. Wheeler (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0.
  4. Arnowitt, Richard; Stanley Deser & Charles W. Misner (1962), "The dynamics of general relativity", in Witten, L., Gravitation: An Introduction to Current Research, Wiley, pp. 227-265.
  5. Komar, Arthur (1959). "Covariant Conservation Laws in General Relativity". Phys. Rev. 113 (3): 934–936. Bibcode 1959PhRv..113..934K. doi:10.1103/PhysRev.113.934.
  6. Bondi H, van de Burg M G J, and Metzner A W K, Proc. R. Soc. London Ser. A 269:21-52 Gravitational waves in General Relativity. VII. Waves from axi-symmetric isolated systems (1962).
  7. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. – 568 с.
  8. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8 (No. 1), pp. 1-16, (2015); статья на русском языке:  Релятивистская энергия и масса в пределе слабого поля.
  9. Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19. // Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.
  10. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06. // Энергия связи и полная энергия макроскопического тела в релятивистской однородной модели.
  11. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5. // Иерархия масс в релятивистской однородной системе.
  12. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; статья на русском языке: Концепция общего силового векторного поля.
  13. Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?

См. также

Внешние ссылки

·         Invariant energy

 

Источник: http://sergf.ru/ie.htm

На список страниц