In English

Принцип суммирования энергий

Из проекта Викизнание

Принцип суммирования энергий произвольной системы задаёт порядок включения различных видов энергии, связанных с системой, в энергетические функции, описывающие состояние системы. Наиболее часто суммирование энергий применяется в теоретической физике, где используется принцип наименьшего действия, вычисляются полные энергии систем и учитывается закон сохранения энергии. Принцип суммирования энергий является с одной стороны методологическим принципом, а с другой стороны – следствием сложности систем, состоящих из вещества в различных состояниях, и имеющихся в данных системах полей. Сложность увеличивается за счёт движения вещества и поля, при переходах вещества из одного фазового состояния в другое, при трансформации энергии полей и вещества друг в друга. Энергетические функции имеют разный смысл в зависимости от их предназначения. Для оценки изменения полной энергии системы необходимо учитывать, что одни компоненты увеличивают энергию, а другие ей уменьшают, что приводит к разным знакам перед компонентами энергии. Если же энергетические функции используются для нахождения уравнений движения, то знаки перед компонентами энергии выбираются из условия соответствия уравнениям движения вещества и поля. В результате для каждой энергетической функции используется свой собственный порядок суммирования энергий.

Оглавление

  • 1 Примеры
    • 1.1 Термодинамические потенциалы
    • 1.2 Функция Лагранжа
    • 1.3 Функция Гамильтона
    • 1.4 Инвариантная энергия
    • 1.5 Релятивистская энергия
    • 1.6 Уравнения для определения метрики

o 1.6.1 Уравнения Эйнштейна-Гильберта

o 1.6.2 Уравнения КТГ

  • 2 Ссылки
  • 3 См. также
  • 4 Внешние ссылки

Примеры

Термодинамические потенциалы

Для вычисления энергетических функций в термодинамике используют такие физические величины, как давление ~P, объём ~V, абсолютная температура ~T, теплоёмкость ~C, масса ~ M, количество вещества ~N. Эти величины достаточно хорошо измеряются, в отличие от энтропии ~S, химического потенциала ~\mu, количества теплоты ~Q, которыми обладает вещество. Внутренняя энергия ~U и её приращение ~dU для многофазного вещества в квазистатическом процессе выражаются формулами:

~U= \int ( T dS - P dV + \sum_i \mu_i dN_i + \delta A'),

~dU= \delta Q - \delta A + \sum_i \mu_i dN_i + \delta A',

где  ~ \delta Q= T dS – приращение количества теплоты, ~ \delta A= P dV – работа, выполняемая системой, ~ i– количество фаз вещества, ~ \delta A' – работа, выполняемая над системой.

Кроме внутренней энергии, в термодинамике имеются и другие связанные с ней энергетические функции, например, свободная энергия Гельмгольца:

~ \mathcal F = U - TS.

Соответственно, приращение свободной энергии Гельмгольца равно:

~d \mathcal F = - S dT - \delta A + \sum_i \mu_i dN_i + \delta A'.

Энтальпия и её приращение имеют вид:

~H=U+PV,  

~dH= \delta Q + V dP + \sum_i \mu_i dN_i + \delta A'.

Энергия Гиббса и её приращение:

~G=U+PV-TS,  

~dG= -S dT + V dP + \sum_i \mu_i dN_i + \delta A'.

Большой термодинамический потенциал и его приращение:

~\Omega = U - TS - \sum_i \mu_i N_i,

~d \Omega = - S dT - \delta A - \sum_i N_i d\mu_i + \delta A'.

Связанная энергия и её приращение:

~E_b = U + PV - \sum_i \mu_i N_i,

~d E_b = \delta Q +V dP - \sum_i N_i d\mu_i + \delta A'.

Возможны ещё два термодинамических потенциала и их приращения:

~P_1 = U - \sum_i \mu_i N_i,

~d P_1 = \delta Q - \delta A - \sum_i N_i d\mu_i + \delta A',

~P_2 = U - TS + PV - \sum_i \mu_i N_i,

~d P_2 = - S dT +V dP - \sum_i N_i d\mu_i + \delta A'.

Порядок сложения компонент энергии оказывается такой, чтобы получался соответствующий термодинамический потенциал, имеющий свой собственный смысл. Так, внутренняя энергия отражает закон сохранения энергии, а изменение свободной энергии Гельмгольца при изотермическом процессе определяется только разностью работы, выполняемой как системой над окружением, так и окружением над системой.

Многие соотношения термодинамики хорошо выполняются не только для газов, но и для жидкостей и вещества в твёрдом состоянии.

Функция Лагранжа

Одним из путей нахождения уравнений движения систем и законов их существования является варьирование функционала действия, то есть варьирование по различным переменным интеграла по времени от функции Лагранжа, с целью определения экстремальных и наиболее вероятных состояний. Функция Лагранжа ~L состоит из ряда компонент энергии, которые в механике входят либо в кинетическую энергию ~ T, либо в потенциальную энергию ~ V. Для нахождения функции Лагранжа в механике записывают разность кинетической и потенциальной энергий:

L=T-V .

Обычно предполагается, что функция Лагранжа зависит только от времени, координат и скоростей, но не от более высоких производных по времени.

Так как вещество в каждой механической системе является источником собственных полей, то в выражение для функции Лагранжа в общем случае добавляются члены, связанные с энергиями этих полей. В специальной теории относительности функция Лагранжа одной частицы с массой ~ M и зарядом ~ q в электромагнитном поле имеет вид: [1]

~L=-Mc{\frac {ds}{dt}}-q{\frac {A_{\mu }dx^{\mu }}{dt}}-{\frac {c\varepsilon _{0}}{4}}\int {F_{{\mu \nu }}F^{{\mu \nu }}{\frac {dx^{4}}{dt}}}=

= - M c^2 \sqrt {1-v^2/c^2} -q(\varphi- \mathbf {A \cdot v}) + \frac {\varepsilon_0}{2} \int {(E^2 -c^2 B^2)} dx^3,

где ~c – скорость света, ~ds – интервал,  ~ A_\mu = \left( \frac {\varphi }{c},-\mathbf {A}\right) – электромагнитный 4-потенциал с нижним (ковариантным) индексом, ~ dx^\mu – 4-вектор смещения частицы, ~ \varepsilon_0 – электрическая постоянная, ~ F_{\mu \nu} – тензор электромагнитного поля, ~ dx^4 =c dtdx^3 =c dtdx{}dy{}dz – элемент 4-объёма, ~ \mathbf {v} – скорость движения частицы, ~ \varphi и ~ \mathbf {A} – скалярный и векторный потенциалы электромагнитного поля соответственно, ~ E и ~B – напряжённость электрического поля и магнитная индукция соответственно.

В данном случае в функцию Лагранжа входят три компоненты с размерностью энергии, связанные с релятивистской энергией частицы, с энергией частицы в электромагнитном поле, и с энергией самого электромагнитного поля. Выражения для компонент энергии и знаки перед ними выбраны таким образом, чтобы в результате варьирования функционала действия получались уравнения движения частицы в поле и уравнения Максвелла для напряжённостей поля.

Аналогично записывается функция Лагранжа для одной частицы в гравитационном поле в лоренц-инвариантной теории гравитации: [2]

~L=-Mc{\frac {ds}{dt}}-M{\frac {D_{\mu }dx^{\mu }}{dt}}+{\frac {c}{16\pi G}}\int {\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}{\frac {dx^{4}}{dt}}}=

=-Mc^{2}{\sqrt {1-v^{2}/c^{2}}}-M(\psi -{\mathbf {D\cdot v}})-{\frac {1}{8\pi G}}\int {(\Gamma ^{2}-c^{2}\Omega ^{2})}dx^{3},

где ~D_{\mu }=\left({\frac {\psi }{c}},-{\mathbf {D}}\right)  – гравитационный 4-потенциал с нижним (ковариантным) индексом, ~ G – гравитационная постоянная, ~ \Phi_{\mu \nu} – тензор гравитационного поля, ~ \psi и ~ \mathbf {D} – скалярный и векторный потенциалы гравитационного поля соответственно, ~ \Gamma и ~\Omega – напряжённость гравитационного поля и поле кручения соответственно, а масса ~ M  не только учитывает сумму масс нуклонов вещества, но и вклад от массы-энергии всех полей, взаимодействующих с веществом и изменяющих величину массы частицы.

После варьирования функционала действия получаются уравнения движения частицы в гравитационном поле и максвеллоподобные гравитационные уравнения для гравитационного ускорения и поля кручения. Для того, чтобы лагранжиан можно было использовать в любых системах отсчёта, его следует записать в ковариантном виде. В искривлённом пространстве-времени интервал можно выразить через метрический тензор ~ g_{\mu\nu}:

~ds = \sqrt {g_{\mu\nu}\ dx^{\mu} \ dx^{\nu}},

а вместо элемента 4-объёма ~ dx^4 при интегрировании по 4-объёму следует использовать произведение ~ \sqrt {-g}dx^4, где ~ g есть детерминант метрического тензора.

Функция Гамильтона

В классической механике функция Гамильтона или гамильтониан системы частиц может быть определён через лагранжиан: ~H=\sum _{i}{{\vec p}_{i}}\cdot {\dot {{\vec q}_{i}}}-L,

где ~\vec p_i — обобщённый импульс i-ой частицы, а ~\dot \vec q_i — её обобщённая скорость.

Для консервативных систем, в которых сохраняется энергия, функция Гамильтона как функция от обобщённых координат и импульсов оказывается равной полной энергии ~ E системы и имеет следующий вид:

~ H=E = T + V.

В этом случае видно, что различие между функциями Лагранжа и Гамильтона заключено в разных знаках перед потенциальной энергией ~ V системы.

Инвариантная энергия

Инвариантная энергия ~E_0 тела определяется как релятивистская энергия, измеренная неподвижным относительно центра импульсов тела наблюдателем. Стандартный подход предполагает суммирование всех видов энергии тела:

~E_0= E_m + E_p + E_T + U +W+ E_L,

где ~E_m – энергия покоя отдельных частиц вещества, ~E_p – энергия давления (сжатия) вещества, понимаемая как потенциальная энергия межатомных взаимодействий, ~E_T – тепловая энергия, дающая в сумме с ~E_p внутреннюю энергию, ~ U – полная гравитационная энергия тела, включающая энергию собственного поля в веществе тела и за его пределами, и гравитационную энергию в поле от внешних источников, ~ W – полная электромагнитная энергия тела, ~ E_L – энергия излучения, взаимодействующего с веществом тела.

В общей теории относительности это приводит к тому, что нагретое тело должно увеличивать свою массу, а масса гравитационно-связанного тела должна быть меньше, чем суммарная масса частиц вещества, из которого образуется данное тело.

Существует альтернативная точка зрения, согласно которой компоненты энергии входят в равенство для инвариантной энергии с отрицательными знаками: [3] [4] [5] [6]  [7]

~E_0= E_m - E_p - E_T - U -W- E_L.

Как следствие, нагретые тела должны иметь меньшую массу, чем холодные, а масса звезды должна быть больше массы рассеянного вещества, из которого она образовалась в ходе гравитационного коллапса.

Третий подход связан с переосмыслением сущности и порядка суммирования энергий в ковариантной теории гравитации (КТГ). Способ вычисления инвариантной энергии существенно зависит от того, каким образом учитывается в энергии скалярная кривизна и космологическая постоянная. В частности, космологическая постоянная может калиброваться таким образом, чтобы исключить скалярную кривизну и тем самым найти однозначное выражение для энергии. [8] Другое нововведение заключается в том, что вместо стандартного тензора энергии-импульса вещества с учётом скалярного давления в рассмотрение вводятся два новых векторных поля – поле ускорений и поле давления, с соответствующими тензорами энергии-импульса. Если добавить сюда электромагнитное и гравитационное поля, получаются 4 поля, симметрично входящие в лагранжиан и в энергию. При вычислении инвариантной энергии для сферического тела в равновесии оказывается, что компоненты энергии всех четырёх полей взаимно сокращаются. Поэтому вклад в инвариантную энергию системы делают лишь потенциальные энергии частиц, находящихся под действием полей. [9] Эти энергии также частично сокращаются, и для инвариантной энергии можно записать:

~E_{0}= Mc^2=m_b c^2 - \frac {3G m^2_b}{10a}+ \frac {3 q^2_b}{40 \pi \varepsilon_0 a}.

Соотношение для масс выглядит следующим образом: ~m' = M < m_ b = m_g,

где масса  ~m_{b}  и заряд  ~q_{b}  вычисляются интегрированием соответствующей плотности по объёму тела радиуса  ~a, масса системы ~Mравна суммарной массе частиц ~m' , масса ~m_{b} равна гравитационной массе ~m_{g} , а превышение ~m_{b}  над ~M происходит за счёт того, что частицы внутри тела двигаются и находятся под давлением в гравитационном и электромагнитном полях.

Более точный результат находится в статьях, [10] [11] где для энергии и масс получается следующее:

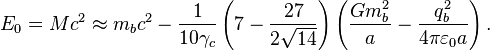
~E_{{0}}=Mc^{2}\approx m_{b}c^{2}-{\frac {1}{10\gamma _{c}}}\left(7-{\frac {27}{2{\sqrt {14}}}}\right)\left({\frac {Gm_{b}^{2}}{a}}-{\frac {q_{b}^{2}}{4\pi \varepsilon _{0}a}}\right).

 

~m'<M<m<m_{b}=m_{g}.

Здесь калибровочная масса  ~m'  связана с космологической постоянной и представляет собой массу-энергию частиц вещества в 4-потенциалах полей системы; ~M есть инертная масса системы; вспомогательная масса  ~m равняется произведению плотности массы частиц на объём вещества системы; масса  ~m_{b}  есть сумма инвариантных масс (масс покоя) частиц системы, равная по величине гравитационной массе  ~m_{g}  системы.

Релятивистская энергия

В отличие от инвариантной энергии, релятивистская энергия в общем случае содержит дополнительные компоненты энергии, связанные с движением системы как целого. В результате в формулах для энергии может быть определена зависимость от скорости, например от скорости движения центра импульсов системы ~v. Если в пространстве Минковского известна инвариантная энергия ~E_0, то релятивистская энергия в произвольной инерциальной системе отчёта находится с помощью преобразования Лоренца по формуле:

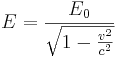~E= \frac {E_0} {\sqrt {1-\frac {v^2}{c^2}} }.

 

Для непрерывно распределённого вещества в искривлённом пространстве-времени выражение для энергии физической системы имеет следующий вид: [12]

~E=\int \left[{\mathbf v}\cdot {\frac {\partial }{\partial {\mathbf v}}}\left({\frac {{\mathcal {L}}_{p}}{u^{0}}}\right)u^{0}-{\mathcal {L}}_{p}\right]{\sqrt {-g}}dx^{1}dx^{2}dx^{3}-\int {\mathcal {L}}_{f}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+\sum _{{n=1}}^{N}\left({\mathbf v}_{n}\cdot {\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right).

 

В данном выражении лагранжиан системы ~{\mathcal {L}} представлен в виде суммы двух частей ~{\mathcal {L}}={\mathcal {L}}_{p}+{\mathcal {L}}_{f}, где ~{\mathcal {L}}_{p} зависит от 4-потенциалов и 4-токов, а ~{\mathcal {L}}_{f} содержит тензорные инварианты полей. Величина ~L_{f}=\int {\mathcal {L}}_{f}{\sqrt {-g}}dx^{1}dx^{2}dx^{3} есть та часть функции Лагранжа, которая получается путём интегрирования ~{\mathcal {L}}_{f} по движущемуся объёму физической системы. В веществе системы скорость частиц есть ~{\mathbf v}, величина ~u^{0} есть временная компонента 4-скорости этих частиц, ~g есть детерминант метрического тензора. При вычислении вклада полей частиц в энергию системы необходимо разделить вещество на ~N частиц или элементов вещества точечных размеров. Каждая такая частица имеет некоторую скорость ~{\mathbf v}_{n}, при этом ~L_{f} и энергия системы ~E в общем случае зависят от скоростей ~{\mathbf v}_{n}.

Для четырёх векторных полей энергия выражается через скалярные потенциалы полей ~\varphi ,\psi ,\vartheta ,\wp , через векторные потенциалы полей ~{\mathbf A},{\mathbf D},{\mathbf U},{\mathbf \Pi }, и через тензоры полей ~F_{{\mu \nu }},\Phi _{{\mu \nu }},u_{{\mu \nu }},f_{{\mu \nu }}:

 

 

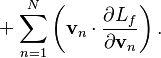
Уравнения для определения метрики

Уравнения Эйнштейна-Гильберта

Уравнения Эйнштейна-Гильберта в общей теории относительности (ОТО) предназначены для поиска метрики в искривлённом пространстве-времени и записываются в тензорном виде:

R_{\mu\nu } - {R \over 2} g_{\mu\nu } + \Lambda g_{\mu\nu } = {8 \pi \beta G\over c^4} T_{\mu\nu },

где ~R_{\mu\nu } — тензор Риччи, ~R — скалярная кривизна, ~\Lambda — космологическая постоянная, а ~T_{\mu\nu } представляет собой тензор энергии-импульса с размерностью объёмной плотности энергии, ~G — гравитационная постоянная Ньютона.

В ОТО ~\beta=1 и в состав тензора ~T_{\mu\nu } как правило входят тензор энергии-импульса вещества ~ \phi_{\mu\nu } и тензор энергии-импульса электромагнитного поля ~ W_{\mu\nu }:

~ T_{\mu\nu} = \phi_{\mu\nu }+ W_{\mu\nu }.

Отсутствие тензора энергии-импульса гравитационного поля как источника, влияющего на метрику, связано в ОТО с тем, что гравитационное поле отождествляется с геометрическим полем в виде метрического поля, причём это поле не порождает само себя (отсутствие самодействия метрического поля).

Уравнения КТГ

В ковариантной теории гравитации (КТГ) уравнения для метрики имеют следующий вид: [8] [13]

R_{\mu\nu } - {R \over 4} g_{\mu\nu } = {8 \pi \beta G\over c^4} T_{\mu\nu },

где коэффициент ~\beta  находится из уравнений движения частиц и волн в каждой заданной форме метрики, а тензор ~T_{\mu\nu }  является суммой четырёх тензоров:

~ T_{\mu\nu} = B_{\mu\nu }+ W_{\mu\nu } + U_{\mu\nu } + P_{\mu\nu },

 

где  ~ U_{\mu\nu }  – тензор энергии-импульса гравитационного поля, ~ B_{\mu\nu } – тензор энергии-импульса поля ускорений, и  ~ P_{\mu\nu } – тензор энергии-импульса поля давления.

Это означает, что в КТГ гравитационное поле является физическим полем и наряду с электромагнитным полем, с полем ускорений и полем давления, является источником, формирующим метрику пространства-времени.

В случае непрерывно распределённого вещества для космологической постоянной получается равенство:

~\Lambda ={16\pi \beta G \over c^{4}}(D_{\kappa }J^{\kappa }+A_{\kappa }j^{\kappa }+U_{\kappa }J^{\kappa }+\pi _{\kappa }J^{\kappa }),

где ~ J^\kappa  и  ~ j ^\kappa являются массовым и электромагнитным 4-током, соответственно, ~U_{\kappa }  и  ~ \pi_\kappa  – 4-потенциалы поля ускорений и поля давления.

Ковариантная производная левой части уравнения для метрики в силу калибровки космологической постоянной и скалярной кривизны даёт нуль. Это позволяет записать уравнение движения вещества как равенство нулю ковариантной производной от суммы тензоров в правой части, взятых с контравариантными индексами:

~ \nabla_\nu ( B^{\mu\nu }+ W^{\mu\nu } + U^{\mu\nu } + P^{\mu\nu } )=0.

 

Общее поле

В концепции общего поля предполагается, что компонентами этого поля являются все векторные поля, связанные с веществом. 4-потенциал общего поля   ~ s_\mu  равен сумме 4-потенциалов частных полей. [14]  [15]  В результате сумма членов в объёмной плотности лагранжиана, ответственных за энергию вещества в различных полях, с точностью до знака равна просто произведению  ~ s_\mu J^\mu. Что касается энергии самих частных полей, то эти энергии включаются в лагранжиан через тензор общего поля  ~ s_{\mu \nu}, получаемый как 4-ротор от 4-потенциала общего поля. Для функции Лагранжа получается соотношение:

~L=\int (kcR-2kc\Lambda -s_{\mu }J^{\mu }-{\frac {c^{2}}{16\pi \varpi }}s_{{\mu \nu }}s^{{\mu \nu }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3},

где ~k  и  ~ \varpi  – постоянные, подлежащие определению, ~ \sqrt {-g} dx^1 dx^2 dx^3  – инвариантный 3-объём, выражаемый через произведение  ~ dx^1 dx^2 dx^3  дифференциалов пространственных координат, и через квадратный корень ~\sqrt {-g}  из детерминанта ~g метрического тензора, взятого с отрицательным знаком.

Релятивистская энергия системы равна:

~E = \int {( s_0 J^0 + \frac {c^2 }{16 \pi \varpi } s_{ \mu\nu} s^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},

где ~ s_0  и  ~ J^0  обозначают временные компоненты 4-векторов  ~ s_{\mu }  и  ~ J^{\mu }.

Особенностью выражения для энергии является то, что в нём энергия общего поля в тензорном произведении  ~ s_{ \mu\nu} s^{ \mu\nu}  включает в себя не только энергии частных полей, но и перекрёстные члены в виде суммы произведений напряжённостей частных полей в различных сочетаниях. Можно сказать, что энергия частиц в частных полях входит в энергию системы линейно, а энергия самих полей – приблизительно квадратичным образом.

 

Ссылки

1.      Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.

2.      Федосин С.Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1. 544 стр., Табл.66, Ил.93, Библ. 377 назв.

3.      Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body. Preprints 2017, 2017040150. http://dx.doi.org/10.20944/preprints201704.0150.v1; статья на русском языке: Энергия, импульс, масса и скорость движущегося тела.

4.      Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of Gravitomagnetic Theory. Canadian Journal of Physics, Vol. 92, No. 10, pp. 1074-1081 (2014). http://dx.doi.org/10.1139/cjp-2013-0683; статья на русском языке: Энергия, импульс, масса и скорость движущегося тела в свете теории гравитомагнетизма.

5.      Fedosin S.G. The Principle of Proportionality of Mass and Energy: New Version. Caspian Journal of Applied Sciences Research, Vol. 1, No. 13, pp. 1-15 (2012). http://dx.doi.org/10.5281/zenodo.890753; статья на русском языке: Принцип пропорциональности массы и энергии: новая версия.

6.      Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804; статья на русском языке: Принцип наименьшего действия в ковариантной теории гравитации.

7.      Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023; статья на русском языке: Гамильтониан в ковариантной теории гравитации.

8.      а б Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; статья на русском языке: О космологической постоянной, поле ускорения, поле давления и об энергии.

9.      Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; статья на русском языке: Релятивистская энергия и масса в пределе слабого поля.

10.  Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06. // Энергия связи и полная энергия макроскопического тела в релятивистской однородной модели.

11.  Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5. // Иерархия масс в релятивистской однородной системе.

12.  Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?

13.  Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских векторных полей.

14.  Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; статья на русском языке: Концепция общего силового векторного поля.

15.  Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017).  http://dx.doi.org/10.1142/S2424942417500025. // Две компоненты макроскопического общего поля.

См. также

Внешние ссылки

 

Источник: http://sergf.ru/pse.htm

На список страниц