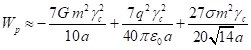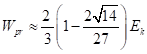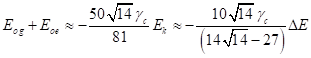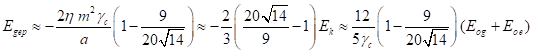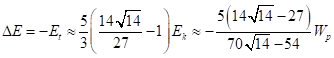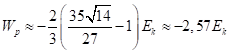Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06
Энергия связи и полная энергия макроскопического тела в
релятивистской однородной модели
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
С помощью ковариантной теории
гравитации точно вычисляются полная энергия, энергия связи, энергия полей, энергия
давления и потенциальная энергия системы из частиц и четырёх полей в релятивистской однородной модели.
Указанные энергии сравниваются с кинетической
энергией частиц. Находятся не зависящие от свойств системы соотношения между
коэффициентами поля ускорений и поля давления, позволяющие выразить
их друг через друга и через гравитационную и электрическую постоянные. Показывается заметное отличие полученных
результатов от соотношений для простых систем в классической механике, в
которых поля ускорений и поля давления не учитываются либо давление
считается простой скалярной величиной. Обосновывается вывод о том, что по мере
образования всё более массивных релятивистских однородных систем средняя
плотность этих систем уменьшается по сравнению со средней плотностью слагающих
эти системы частиц или тел. При этом инертная масса массивной системы
оказывается меньше суммарной инертной массы частей системы.
Ключевые слова: релятивистская однородная система; энергия связи; полная энергия; энергия давления; потенциальная энергия; кинетическая энергия.
The binding
energy and the total energy of a macroscopic body in the relativistic uniform
model
Sergey G. Fedosin
PO
box 614088, Sviazeva
str. 22-79, Perm, Perm Krai, Russia
E-mail:
fedosin@hotmail.com
With the help
of the covariant theory of gravitation the total energy, binding energy, energy
of fields, pressure energy and the potential energy of the system consisting of
particles and four fields is precisely calculated in the relativistic uniform
model. These energies are compared with the kinetic energy of particles. The
relations between the coefficients of the acceleration field and the pressure
field independent of the system’s properties are found, which can be expressed
in terms of each other and in terms of the gravitational constant and the
vacuum permittivity. A noticeable difference is shown between the obtained
results and the relations for simple systems in classical mechanics, in which
the acceleration field and pressure field are not taken into account or the
pressure is considered to be a simple scalar quantity. The conclusion is
substantiated that as increasingly massive relativistic uniform systems are
formed, the average density of these systems decreases as compared to the
average density of the particles or bodies making up these systems. In this
case the inertial mass of the massive system is less than the total inertial
mass of the system’s parts.
Keywords: relativistic uniform system; binding energy; total
energy; pressure energy; potential energy; kinetic
energy.
1.
Введение
По определению, релятивистская энергия системы включает в себя все виды энергии и должна записываться в ковариантном виде. В некоторых случаях из релятивистской энергии вычитают постоянный член в виде энергии покоя частиц системы. Так получается полная энергия системы, с которой обычно имеют дело в классической механике при решении простейших задач, не требующих релятивистского подхода. Как правило, полную энергию разбивают на две основные части – кинетическую энергию и потенциальную энергию.
В больших макроскопических системах могут одновременно действовать несколько полей, каждое из которых изменяет энергию частиц и может ещё иметь свою собственную потенциальную энергию. Это существенно усложняет выражения для релятивистской и полной энергий и зачастую приводит к тому, что разные теории поля дают не совпадающие по форме выражения для энергий. Например, в общей теории относительности энергия гравитационного поля вычисляется не прямо, а косвенно, с помощью псевдотензора энергии-импульса и предварительно найденной метрики пространства-времени [1]. Это означает, что знание метрики системы является обязательным для определения энергии даже в случае предельно слабого поля. Но даже при известной метрике возникает неоднозначность при определении релятивистской энергии и инертной массы системы и отдельных её частей [2], [3].
В противоположность этому, в ковариантной теории гравитации имеется тензор энергии-импульса гравитационного поля, а метрика любой системы в пределе слабого поля плавно переходит в постоянную метрику пространства Минковского, где гравитационная энергия перестаёт зависеть от вида метрики системы [4]. Аналогично, в земных условиях метрика пространства-времени практически не используется для вычисления энергии электромагнитного поля тел.
С учётом этого мы определим далее в рамках ковариантной теории гравитации и релятивистской однородной модели полную энергию и энергию связи макроскопического тела, находящегося в равновесии без вращения, и сравним полученные выражения с результатами для простых систем в классической механике. Мы вычислим также отдельные компоненты энергии, включая энергию полей, энергию давления и потенциальную энергию системы. Наш подход использует теорию поля в ковариантной записи, так что полученные для плоского пространства-времени результаты в случае необходимости будет нетрудно уточнить для искривлённого пространства-времени с соответствующей метрикой.
Термодинамические свойства рассматриваемой нами физической системы из частиц и полей ранее уже изучались Черниковым (Chernikov system of particles and fields) методами релятивистской кинетической теории газов и статистической физики [5]. Для случая самогравитирующей системы с заряженными частицами существует специальное название – плазма Власова (Vlasov plasma). Власов использовал дополнительную идею самосогласованного поля [6] и указал на ограничения модели с парными столкновениями Больцмана, не учитывающей действия электромагнитного и гравитационного полей на расстоянии. Однако наш подход основывается не на кинетической теории, а на теории векторных полей, и вместо общей теории относительности используется ковариантная теория гравитации. Кроме этого, взаимодействия частиц мы описываем полями с собственными 4-потенциалами, причём это относится и к полю давления, и к полю ускорений частиц. Таким образом, получение средних значений физических величин связывается не с функциями распределения, не с фазовым пространством и с теоремой Лиувилля (Liouville's theorem), а с усреднением физических величин непосредственно в уравнениях, вытекающих из принципа наименьшего действия.
Несмотря на то, что приближение постоянной инвариантной плотности массы в присутствии достаточно сильных гравитационных полей является некоторым ограничением, такой подход является оправданным, поскольку даёт точное описание и вполне применимо к ряду макроскопических систем типа наблюдаемой Вселенной, космических газовых облаков и даже нейтронных звёзд. Кроме этого, предлагаемый подход может быть уточнён и для случая неоднородной плотности массы, как это было сделано в [7] для белых карликов и Солнца, являющегося звездой главной последовательности.
2. Релятивистская
и кинетическая энергии
В [8] в рамках ковариантной теории гравитации была найдена формула для вычисления релятивистской энергии физической системы из частиц и полей, связанных с этими частицами. При этом учитывались электромагнитное и гравитационное поля, поле ускорений и поле давления, а роль тензора энергии-импульса вещества играл тензор энергии-импульса поля ускорений. Аналогичная формула для энергии представлена в концепции общего поля для макроскопической системы в [9, 10].
С помощью этой формулы в [4] энергия для равновесной системы с непрерывно распределённым хаотически движущимся веществом с учётом энергии полей была вычислена в явном виде с точностью до членов, не содержащих в знаменателях квадрат скорости света. С учётом поправок, сделанных в [11], энергия равна:
. (1)
В (1) предполагается, что система имеет сферическую форму
радиуса 
, масса 
и заряд 
системы получаются
умножением плотности массы 
и плотности заряда
на объём неподвижной
сферы, причём и – инвариантные плотности
частиц, составляющих сферу, измеренные в сопутствующих частицах системах
отсчёта. В рамках релятивистской однородной модели данные плотности считаются
постоянными величинами. Ввиду хаотичности движения вещества глобальные
векторные потенциалы и соответствующие соленоидальные векторы полей системы считаются
равными нулю, так что вклад соленоидальных векторов в энергии (1) не
учитывается.
В центре сферы скорость
частиц есть 
и фактор
Лоренца частиц равен 
,
где 
есть скорость света. Каждое поле характеризуется своим
собственным коэффициентом: 
– коэффициент поля
ускорений, 
– гравитационная
постоянная, 
– электрическая
постоянная, 
– коэффициент поля
давления. Величина 
в (1) представляет
собой скалярный потенциал поля давления в центре сферы, а масса 
является релятивистской
инвариантной инертной массой системы.
Кинетическая энергия движения частиц данной системы была найдена в [12] тремя способами – с помощью теоремы вириала, путём вычитания энергии покоя частиц из релятивистской энергии их движения, и через обобщённые 3-импульсы частиц системы. Все эти способы дают один и тот же результат:
Выражения (1) и (2) являются исходной точкой для определения компонент
полной энергии и энергии связи рассматриваемой системы. Численный коэффициент 
в (2) является
следствием решения квадратного уравнения для скорости в центре сферы и
представляет собой свойство релятивисткой однородной системы. В результате подобные
численные коэффициенты появляются и в некоторых других компонентах энергии.
3. Компоненты полной
энергии
Согласно
[13], фактор Лоренца частиц, хаотически движущихся внутри сферы, зависит от
текущего радиуса 
:
.
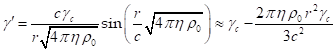(3)
Фактор
Лоренца максимален в центре сферы, где частицы движутся с наибольшей скоростью.
Мы используем систему отсчёта 
, которая связана с центром сферы, так что все результаты
будут относиться к неподвижной относительно наблюдателя сфере. В случае
необходимости энергии и импульсы отдельных полей и системы в целом могут быть
пересчитаны в лабораторную систему отсчёта 
с помощью
соответствующих преобразований Лоренца при известной скорости движения сферы в .
Формула
(3) была получена путём решения волнового уравнения для скалярного потенциала 
поля ускорений
аналогично тому, как внутри сферы вычисляются потенциалы электромагнитного или
гравитационного поля. При этом в пространстве Минковского потенциал поля
ускорений становится пропорциональным фактору Лоренца: 
.
Физической причиной радиальной зависимости в (3) является необходимость поддержания баланса действующих сил. Так, гравитационная сила стремится сжать вещество, а давление движущихся частиц противостоит такому сжатию. Действительно, напряжённость гравитационного поля внутри однородной системы сферической формы пропорциональна текущему радиусу и направлена к центру сферы. Объёмная плотность гравитационной силы пропорциональна напряжённости поля и плотности массы вещества. По мере перемещения точки наблюдения от поверхности к центру вдоль радиуса увеличивается общая толщина и масса наблюдаемого сферического слоя, а также суммарная гравитационная сила со стороны этого слоя в направлении к центру. Гравитационное давление уравновешивается динамическим давлением частиц, которое согласно кинетической теории составляет две трети кинетической энергии частиц, приходящейся на единицу объёма. Следовательно, чем ближе к центру, тем больше должно быть давление частиц в веществе.
Гравитация
также формирует некоторую сферическую границу системы радиуса такую, что частицы в
среднем не выходят за этот радиус. Если бы 
заряженных частиц были
замкнуты внутри сферы с жёсткой границей, то в равновесном состоянии и в отсутствие
массовых сил можно было бы ожидать однородной плотности массы, одной и той же скорости
и постоянного фактора Лоренца частиц в каждой точке системы, которые зависели
бы лишь от температуры. Однако в нашей модели жёсткой границы нет, а в качестве
массовых сил выступают проникающие в любую точку системы собственные гравитационные
и электромагнитные силы. Таким образом получается, что скорость частиц и их
фактор Лоренца максимальны в центре рассматриваемой системы и уменьшаются при
увеличении текущего радиуса.
Учтём
теперь, что как следствие релятивистского эффекта сокращения длины движущиеся
частицы в специальной теории относительности должны рассматриваться так, что
они имеют уменьшенный объём и увеличенную плотность. Действительно, 
есть плотность массы в
сопутствующих частицам системах отсчёта, 
представляет собой
фактор Лоренца движущихся частиц, а 
даёт
плотность массы этих частиц с точки зрения неподвижного относительно сферы
наблюдателя.
Для
движения частиц между ними должны быть какие-то промежутки. Чтобы вычислить
объём сферы, необходимо просуммировать объёмы всех движущихся внутри сферы типичных
частиц, а также объёмы пустот между ними. Предположим теперь, что размеры типичных частиц намного больше, чем промежутки
между частицами, а объём пустот существенно меньше суммарного объёма частиц. В этом
случае можно воспользоваться приближением сплошной среды, так что элемент массы
вещества внутри сферы будет определяться приблизительным выражением 
, где 
есть элемент объёма
неподвижной сферы.
На
вопрос о том, допустимо ли увеличивать размеры типичных частиц до предела,
необходимого для использования приближения сплошной среды, можно ответить
следующее. В гравитационном поле ускорение частиц не зависит ни от массы, ни от
плотности частиц, что следует из принципа эквивалентности в общей теории
относительности, и из уравнения движения в ковариантной теории гравитации. Для
электрических сил ускорение пропорционально отношению плотностей 
и не зависит от массы
частиц. Это же относится к скорости движения, фактору Лоренца, кинетической
энергии и другим величинам, которые определяются не массой частиц, а их
плотностью . Таким образом, при заданной плотности мы можем выбирать
массу и следовательно, размеры типичных частиц в нужных нам пределах.
Стандартная
формула для вычисления кинетической энергии всех 
частиц системы имеет вид:
.
Масса 
и фактор Лоренца 
частиц были заменены в
[12] соответственно на 
и 
, а сумма по частицам была заменена на интеграл по объёму
сферы. Это привело к соотношению (2) для кинетической
энергии частиц, в котором присутствует ещё выражение для суммарной энергии
покоя частиц сферы с точки зрения связанного со сферой наблюдателя:
.
(4)
Для того
чтобы получить полную энергию системы, нужно из релятивистской энергии (1)
вычесть энергию 
:
.
С другой стороны, согласно (2)
.
После исключения
в этих равенствах с учётом (1) и
приведения подобных членов следует выражение для полной энергии:
. (5)
Полная
энергия должна складываться из кинетической и потенциальной энергий, 
, следовательно, потенциальная энергия системы будет такова:
Как видно, потенциальная энергия (6) содержит энергию частиц в гравитационном и электромагнитном полях и в поле давления, а также энергию самих этих полей, с добавкой энергии поля ускорений.
Для
упрощения выражения (6) используем определение скалярного потенциала поля
давления в [14], согласно которому потенциал в центре сферы равен 
, то есть определяется через давление 
в системе отсчёта 
движущейся частицы. С
другой стороны, скалярный потенциал поля давления с точки зрения наблюдателя в 
равен 
,
где 
– давление, 
– плотность массы в
центре сферы для этого наблюдателя. Следовательно, 
, и давление в системе за счёт движения частиц растёт более
быстро, пропорционально квадрату фактора Лоренца, по сравнению с плотностью
массы, которая растёт пропорционально фактору Лоренца.
Если не
учитывать давления излучения, для давления в системе отсчёта 
частицы и для давления
в центре сферы в системе отсчёта 
можно записать:
, 
,
где 
есть параметр,
представляющий собой число нуклонов на одну единицу релятивистского
ионизованного газа, 
– атомная единица
массы, 
– постоянная
Больцмана, а температура в центре сферы 
в системе отсчёта преобразуется при
переходе из в в
температуру 
.
С учётом
этого скалярный потенциал может быть выражен
через температуру 
в центре сферы:
.
(7)
В [12] была сделана оценка квадрата скорости частиц в центре сферы:
. (8)
При
выводе (8) величина коэффициента 
поля ускорений никак
не фиксировалась, так же, как и масса частиц системы. В реальных телах возможно
наличие одновременно нескольких видов частиц с различными массами, таких как
атомы, ионы, электроны и отдельные нуклоны. Удобно считать, что коэффициент относится к частицам с
эффективной массой 
. В этом случае для плотности массы 
в произвольной точке
сферы можно записать:
,
где 
– концентрация
нуклонов, 
– концентрация частиц
с эффективной массой 
, вносящих вклад в давление, так что 
.
Умножим соотношение
(8) для 
на 
и приравняем к 
, что даёт равенство между кинетической энергией одной
частицы массы 
и кинетической
температурой в центре сферы:
Подставим
левую часть этого равенства в (7) вместо 
и учтём определение 
:
. (9)
Согласно [13], для скалярного потенциала поля давления внутри сферы справедливо соотношение:
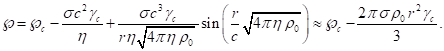(10)
Если в (3) перейти от факторов Лоренца к квадратам скоростей, получим:
.
Путём
умножения этого равенства на 
перейдём к соотношению
для температур внутри сферы:
.
Пойдём
дальше и умножим последнее равенство на 
. С учётом определения и (7) имеем:
.
Из сравнения этого соотношения с (10) приходим к тому, что
Воспользуемся
теперь соотношением между коэффициентами полей, полученным в [7] с помощью уравнения движения:
. (12)
Сочетание (11) и (12) даёт для коэффициентов поля давления и поля ускорений:
, 
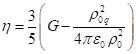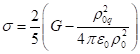. (13)
Подставим теперь (11) в (9):
.
(14)
С учётом (14) просуммируем все члены с давлением в (6):
. (15)
С учётом (15) для потенциальной энергии (6) имеем:
. (16)
Соотношение
(12) можно применить для исключения коэффициента 
в (16) и выражения
потенциальной энергии системы лишь через соответствующие энергии
гравитационного и электромагнитного полей и поля давления:
Выразим
теперь все члены в (16) через коэффициент поля ускорений , используя (12) и (11):
. (18)
Отсюда видно, что потенциальная энергия релятивистской однородной системы, находяшейся в равновесии, всегда отрицательна.
Подстановка (2) в (18) даёт:
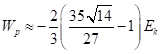. (19)
Соответственно, полная энергия становится равной:
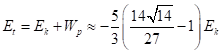. (20)
Несмотря
на то, что в (19) модуль потенциальной энергии много больше кинетической
энергии, в рассматриваемой системе выполняется теорема вириала. Это было
показано в [12], где в явном виде
были вычислены не равный нулю вириал системы и силы, действующие на частицы. В
частности, средняя энергия, связанная с этими силами, с учётом (2) оказывается
равной:
.
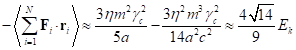Мы можем ещё преобразовать энергию давления (15), используя (11), и сравнить с кинетической энергией (2):
Вся энергия, связанная с давлением, получается почти в 2 раза меньше кинетической энергии движения частиц.
Большинство космических тел являются нейтральными, их
электромагнитные поля можно не учитывать и положить, что 
. В этом случае
согласно (13) 
, а потенциальная энергия (18) становится равной:
.
В классической однородной модели вещество тела сжимается гравитационными силами, которым противостоит сила внутреннего давления, причём давление считается скалярной величиной. Предполагается, что основной вклад в потенциальную энергию вносит гравитационная энергия, равная величине
.
Мы
видим, что потенциальная энергия 
в релятивистской
однородной модели очень близка по величине к гравитационной энергии 
. Это объясняет тот факт, почему в классическом модели для оценки
потенциальной энергии системы достаточно подсчитать лишь полную гравитационную
энергию системы и при этом не учитывать ни энергию поля давления, ни энергию
поля ускорений.
4. Энергия связи
По определению, энергия связи физической системы получается
путём вычитания релятивистской энергии 
(1) из суммарной
энергии покоя частиц 
(4):
. (22)
Учитывая определение полной энергии 
, с учётом (20) для энергии связи находим:
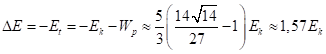. (23)
Для сравнения, в простых системах, где действуют только
потенциальные силы в отсутствие давления, в силу теоремы вириала 
.
В нашей физической системе из тесно взаимодействующих частиц
и полей в дополнение к электромагнитному полю мы учитываем ещё вклады от гравитационного
поля, от поля ускорений и от поля давления. В такой системе согласно (19)
потенциальная энергия полей 
отрицательна и по
модулю намного больше кинетической энергии 
, по сравнению с простыми системами. Это и приводит к
увеличенной энергии связи, необходимой для того, чтобы оторвать частицы системы
друг от друга и разнести их на бесконечность. Таким образом следует ожидать,
что при образовании под действием поля гравитации связанной релятивистской
однородной системы с заряженными частицами, с учётом вкладов поля ускорений и
поля давления из системы должна излучиться энергия, равная энергии связи 
.
Из всех энергий удобнее всего вычислять энергии гравитационных и электромагнитных полей, выходящих за пределы системы вплоть до бесконечности. Сумма энергий этих внешних полей с учётом (12) и (11) равна:
. (24)
Из (4) следует соотношение:
.
Аналогичным образом в [4] заряд 
был связан с
зарядом 
сферы, который
обнаруживает наблюдатель в 
:
.
Применяя это к (24), находим:
. (25)
В (25) энергия гравитационного и электромагнитного полей за
пределами сферы выражена через суммарную массу покоя 
частиц внутри сферы и
суммарный заряд частиц 
. Из (25) видно, что масса фактически равна
гравитационной массе 
, ответственной за гравитацию за пределами тела.
Сравнение (24) с кинетической энергией (2) и с энергией связи (23) даёт следующее:
С помощью (26) мы можем быстро оценить энергию связи 
, зная массу, заряд и радиус системы, с помощью которых в (24)
и в (25) вычисляется сумма энергий 
за пределами системы.
Хотя космические тела при одинаковых массах и размерах могут отличаться
состоянием своего вещества, энергия связи этих тел в (23) согласно (26) будет
одна и та же. Действительно, фазовые превращения вещества, обусловленные
перетоком энергии внутри системы с постоянными радиусом и массой, не должны влиять
на энергию внешних полей и общую энергию связи системы.
5. Оценка энергии полей
В данном разделе рассмотрим вопрос о том, какой вклад в
релятивистскую энергию и в полную энергию вносит энергия 
, связанная с полями системы. Энергия вычисляется через
интегралы по объёму от тензорных инвариантов полей, для чего надо знать
напряжённости и соленоидальные векторы полей. Будучи частью релятивистской
энергии системы (1), энергия согласно [4] равна:
.
Учтём в этом выражении (12), (11), (24), (2), (26) и (23):
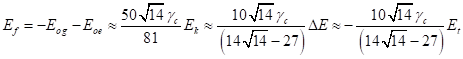. (27)
Согласно (27), энергия всех четырёх полей приблизительно в 
раз больше
кинетической энергии частиц и в 
раз больше энергии
связи , которая по модулю равна полной энергии системы 
. Кроме этого, в (27) 
, то есть с точностью до знака энергия 
равна сумме энергий
гравитационного и электромагнитного полей за пределами сферы. Отсюда следует,
что сумма энергий всех полей внутри сферы равна нулю.
Вычислим теперь сумму энергий частиц 
в гравитационном и
электромагнитном полях и в поле давления. Согласно (1) имеем:
.
Используя (12), (14), (11), (2) и (24), находим:
.
Сравнение с (27) даёт:
. (28)
то есть энергия , связанная с полями, по модулю оказывается более чем в 2
раза меньше, чем сумма энергий частиц в гравитационном и
электромагнитном полях и в поле давления. Заметим, что все выводы сделаны в
приближении слабых полей, когда фактор Лоренца 
частиц в центре сферы
мало отличается от единицы.
Как было показано в [12], хотя глобальные векторные потенциалы полей внутри
сферы с частицами равны нулю,
остаются ещё собственные векторные потенциалы полей внутри самих частиц за счёт
их движения. Эти векторные потенциалы входят в обобщённый импульс, с помощью
которого можно оценить кинетическую энергию частиц системы. Благодаря
собственным векторным потенциалам при движении частиц возникают соответствующие
соленоидальные поля, которые делают добавочный вклад в энергию полей частиц 
.
Какой величины может быть этот вклад? Благодаря
движению, энергия полей становится зависящей от скорости, однако суммарная
энергия полей внутри тела обращается в нуль. Если считать справедливым то же
самое и в отношении каждой из частиц, заполняющих сферу в рассматриваемой нами
модели, то собственные скалярные и векторные потенциалы полей внутри частиц не
приводят к какой-либо суммарной энергии полей. В то же время глобальные
скалярные потенциалы полей, являющиеся скалярной суперпозицией внешних скалярных
потенциалов отдельных частиц, дают соответствующие напряжённости полей, с
помощью которых и вычисляется энергия полей 
внутри и снаружи
сферы.
В отличие от этого, глобальные векторные потенциалы полей являются векторной суперпозицией внешних векторных потенциалов отдельных частиц, и они равны нулю благодаря хаотичности движения множества частиц системы. Отсюда следует равенство нулю всех глобальных соленоидальных векторов, и тем самым они не вносят вклада в энергию полей.
6. Заключение
Наш анализ энергии для системы сферической
формы показывает, что в реальных массивных телах возникают заметные отклонения
полной, кинетической и потенциальной энергий от выражений для энергий простых
систем, взаимодействующих лишь с помощью гравитационных и электромагнитных сил
на расстоянии. Это происходит благодаря дополнительным вкладам от поля
ускорений и поля давления.
С учётом (23) и (19-20) энергия связи и полная энергия могут быть выражены через кинетическую энергию частиц либо через потенциальную энергию системы:
(29)
Полученные нами соотношения (29) можно
сравнить со стандартным выражением для простых систем и с соответствующей
теоремой вириала в классической механике:
, 
, (30)
где классическая потенциальная энергия
выражается в виде суммы по всем частицам через радиус-векторы частиц и силы,
действующие на частицы со стороны потенциальных полей:
.
В отличие от (30), в [12] мы получили
следующее выражение для теоремы вириала:
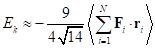. (31)
Из (29) и (31) следует, что учёт поля
ускорений и поля давления в рассматриваемой нами системе приводит к изменению
от классического значения 
до приблизительно 
доли энергии связи по отношению к
потенциальной энергии, и к соответствующему изменению от значения 
до приблизительно 
доли кинетической энергии по отношению к
энергии, связанной с действием потенциальных сил. Кроме этого
из (29) и (31) следует неравенство потенциальной энергии и энергии, связанной с
силами, действующими на частицы, так что 
.
Энергия связи системы согласно (26) может
быть выражена через сумму энергий гравитационного и электромагнитного полей за
пределами тела:
. (32)
Однозначная связь между полной,
кинетической и потенциальной энергиями, и энергией связи в рассматриваемой
системе получается благодаря тому, что мы используем эффективную
массу частиц 
, связанную через параметр 
(количество нуклонов
на одну частицу релятивистского газа) с состоянием вещества системы. Это
приводит к связи коэффициентов поля ускорений и поля давления в (11), и к связи
этих коэффициентов с гравитационной и электрической постоянными в (12-13), что
позволяет сравнивать энергии по величине.
В последнем разделе мы оценили вклад энергии 
, вносимый полями в релятивистскую энергию 
, и сравнили его с энергией 
в гравитационном и
электромагнитном полях и в поле давления в соотношении (28). С помощью (2) и
(4) получается соотношение:
.
Учитывая это, из (1) и (26-28) для релятивистской энергии системы находим:
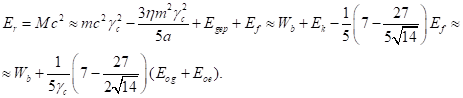(33)
Выражение (33) для релятивистской энергии с учётом (32)
соответствует выражению (22) для энергии связи системы.
Поскольку 
есть энергия покоя
частиц системы согласно (4), а энергия полей 
за пределами сферы как
правило отрицательна за счёт преобладающего вклада гравитационной энергии над
электромагнитной энергией, то видно, что инертная масса 
системы получается меньше,
чем суммарная инвариантная масса частиц 
, входящая в равенство 
. Заметим ещё, что масса точно равна
гравитационной массе 
согласно [4].
После подстановки (25) в (33) приходим к соотношению,
которое лишь незначительно отличается от соотношения (31) в [4]:
.
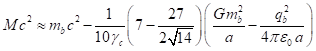(34)
Отсюда следует, что привнесение
в систему заряда 
как правило
увеличивает инертную массу 
, по крайней мере
это выполняется точно при неизменной массе . И наоборот, поскольку 
, возможен случай уменьшения гравитационной массы системы при увеличении
заряда 
. Чтобы увидеть это, достаточно разрешить (34) как квадратное
уравнение для 
и зафиксировать
инертную массу при изменении :
.
В классической однородной системе
сферической формы с неподвижными частицами полная гравитационная энергия в
сумме с полной электрической энергией равны следующему: 
. Следовательно, (34) можно записать так:
.
Как видно, инертная масса релятивистской
однородной системы отличается от массы покоя частиц приблизительно на
половину полной массы-энергии гравитационного и электрического полей
классической однородной
системы, причём наличие электрического поля увеличивает массу , в противоположность действию гравитационного поля.
Представим теперь, что для внешнего наблюдателя сфера с частицами имеет
инвариантную инерциальную массу , объём 
и соответствующую
плотность массы 
: 
. Подставим (4) в (33) и учтём (24) и соотношение 
. Это даёт:
.
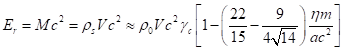(35)
В [12] было найдено выражение (8) для
квадрата скоростей частиц в центре сферы, с помощью которого можно оценить
значение фактора Лоренца:
.
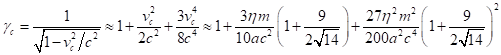Подставляя выражение для 
в (35), находим после
сокращения на 
:
.
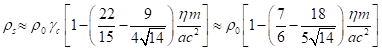(36)
Отсюда следует, что 
, то есть по мере образования всё более массивных
релятивистских однородных систем средняя плотность этих систем уменьшается по
сравнению со средней плотностью слагающих эти системы частиц или тел.
Предположим, что данный вывод справедлив для нейтронных
звёзд, состоящих в основном из одних нуклонов с малой примесью атомных ядер и
некоторого количества электронов, дающих небольшой вклад в общую массу. Будем
считать, что плотность массы 
в (36) представляет собой
плотность вещества нуклонов, а 
есть средняя плотность
нейтронной звезды, и используем (13) для случая незаряженной звезды с равной
нулю плотностью заряда 
. Это даёт:
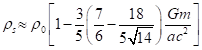. (37)
Подставляя сюда вместо 
массу типичной звезды
1,35 солнечных масс, беря в качестве плотности нуклонов плотность протона 
кг/м3
при радиусе протона 
м согласно [15], и
используя оценку плотности звезды в виде 
, находим соответствующий
радиус нейтронной звезды: 
км. Данный радиус предполагает
плотную упаковку нейтронов в веществе звезды и по порядку величины находится в
разумном согласии с данными наблюдений. Однако следует
учесть, что в звезде между нуклонами имеются промежутки. Поэтому в качестве в (37) следует
подставлять не плотность массы протона, а некоторую меньшую величину. Это
приводит к уменьшению 
, так что радиус 
км ограничивает радиус
нейтронной звезды снизу.
В теории бесконечной вложенности материи нуклоны подобны по своим свойствам нейтронным звёздам, и для этих объектов отношение центральной плотности к средней плотности равно приблизительно 1,5 согласно [7, 15]. Таким образом, в первом приближении нуклоны и нейтронные звёзды по своим свойствам достаточно близки к релятивистским однородным системам. Дополнительно следует принять во внимание, что эти объекты состоят из частиц, для которых необходимо как минимум учитывать энергию собственного спинового вращения и энергию сильного взаимодействия. Следовательно, наш анализ в отношении столь релятивистских объектов требует уточнения, начиная с введения дополнительных членов в лагранжиан и кончая учётом метрики в уравнениях, вытекающих из принципа наименьшего действия. Пока такие расчёты ещё не сделаны, но мы можем ориентироваться на уравнение, выведенное Толменом, Оппенгеймером и Волковым (Tolman-Oppenheimer-Volkoff equation) в рамках общей теории относительности [16].
Из (36) и (33) следует, что по мере
образования некоторой большой релятивистской однородной системы из множества мелких
релятивистских однородных систем, уменьшается средняя плотность массы системы
по сравнению со средней плотностью частей, при этом инертная (инвариантная)
масса большой системы оказывается меньше суммы инертных (инвариантных) масс
частей системы. Параллельно с этим уменьшается плотность релятивистской энергии
и плотность энергии связи при переходе ко всё более массивным объектам. Качественно уменьшение плотности массы и энергии
можно объяснить наличием между отдельными частями системы промежутков с
уменьшенной плотностью массы. Количественно уменьшение средней плотности
системы выводится через вклады энергии частиц в потенциалах собственных полей системы,
с добавкой от энергии полей, находимой через напряжённости и соленоидальные
векторы полей.
В связи с этим заметим, что
напряжённости и соленоидальные векторы полей являются временными и
пространственными скоростями изменения потенциалов полей, поскольку вычисляются
через частные производные от скалярных и векторных потенциалов. Поэтому в
случае известных зависимостей потенциалов полей от времени и координат легко
достигается полное описание системы и нахождение основных зависимостей, включая
уравнение движения и тензор энергии-импульса [14]. В противоположность
этому, если заданы лишь напряжённости
и соленоидальные векторы полей, то для определения потенциалов требуется произвести
интегрирование и учесть начальные условия. А такое интегрирование, как
известно, существенно сложнее операции дифференцирования. Дополнительным преимуществом
использования потенциалов в физике поля является ещё то, что они вычисляются
стандартным образом через соответствующие волновые уравнения [4], [13].
Список использованных источников
1. Ландау Л. Д., Лифшиц Е. М. Теория поля. –
Издание 7-е, исправленное. – М.: Наука, 1988. – 512 с. – (Теоретическая физика,
том II).
2.
Денисов В.И., Логунов А.А. Инертная масса, определенная в
общей теории относительности, не имеет физического смысла. ТМФ, 1982, том 51, номер 2,
163-70; Denisov V.I., Logunov A.A. The inertial mass defined in the general
theory of relativity has no physical meaning. Theoretical and Mathematical
Physics, Volume 51, Issue 2, pp. 421-426 (1982). http://dx.doi.org/10.1007/BF01036205.
3. Khrapko R.I. The Truth about the Energy-Momentum
Tensor and Pseudotensor. ISSN 0202-2893,
Gravitation and Cosmology, Vol. 20, No. 4, pp. 264-273 (2014). Pleiades
Publishing, Ltd., 2014. http://dx.doi.org/10.1134/S0202289314040082;
Храпко Р.И. Правда
о тензоре и псевдотензоре энергии-импульса.
4. Fedosin
S.G. Relativistic Energy and Mass in the Weak Field
Limit. Jordan Journal of
Physics. Vol. 8, No. 1, pp.
1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого
поля.
5.
Chernikov N.A.
Derivation of the equations of relativistic hydrodynamics from the relativistic
transport equation. Physics Letters, Vol. 5, No. 2, pp. 115-117 (1963).
6.
Vlasov A.A. On Vibration Properties of Electron Gas. J. Exp.
Theor. Phys. (in Russian). Vol. 8 (3), 291 (1938).
7. Fedosin S.G. Estimation of the physical parameters
of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка
физических параметров планет и звёзд в модели гравитационного равновесия.
8. Fedosin
S.G. About the cosmological constant, acceleration
field, pressure field and energy. Jordan Journal of
Physics. Vol. 9, No. 1, pp.
1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; О космологической постоянной, поле ускорения,
поле давления и об энергии.
9. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, P. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; Концепция общего силового векторного поля.
10. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025; Две компоненты макроскопического общего поля.
11.
Fedosin S.G. The
Gravitational Field in the Relativistic Uniform Model within the Framework of
the Covariant Theory of Gravitation. International Letters of Chemistry,
Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
12.
Fedosin S.G. The
virial theorem and the kinetic energy of particles of a macroscopic system in
the general field concept. Continuum Mechanics and
Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и
кинетическая энергия частиц макроскопической системы в
концепции общего поля.
13. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12; Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.
14.
Fedosin S.G. The procedure of finding the stress-energy
tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol.
8, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101; Процедура для нахождения
тензора энергии-импульса и уравнений векторного поля любого вида.
15.
Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic
Journal, Vol.
35, No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451; Радиус протона в самосогласованной модели.
16.
Oppenheimer J.R., Volkoff G.M. On Massive
Neutron Cores. Physical Review. Vol. 55 (4), 374-381 (1939). http://dx.doi.org/10.1103/PhysRev.55.374.
Источник: http://sergf.ru/be.htm