На русском языке
Invariant energy
Invariant energy of an arbitrary physical system is a
positive quantity, which consists of all types of energies of the system, and
is equal to the relativistic energy, measured by the observer who is fixed
relative to the center of momentum of the system. The invariant energy usually
includes the rest energy of the matter; the potential energy of the proper
electromagnetic and gravitational fields associated with the system; the
internal energy of the system’s particles; the energy of the system in external
fields; the energy of emission interacting with the system. The invariant
energy ![]() of a particle equals to its rest energy and due to the principle of
mass–energy equivalence is associated with the inertial invariant
mass
of a particle equals to its rest energy and due to the principle of
mass–energy equivalence is associated with the inertial invariant
mass ![]() of the particle by the equation:
of the particle by the equation:
![]() ,
,
where ![]() is the speed of light.
is the speed of light.
The order of calculating the invariant energy through
various types of energy of the system is determined by the principle of energies summation.
Contents
o
1.3
Massive body o 1.3.1 General
relativity o 1.3.2 Covariant
theory of gravitation
|
Relationship with other physical
variables
One particle
In the special relativity, the invariant energy of a point particle can be
calculated either through its relativistic energy ![]() and
momentum
and
momentum ![]() , or through the relativistic energy and
the velocity
, or through the relativistic energy and
the velocity ![]() :
:
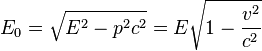 .
.
The relation ![]() holds for the photon, so that the invariant energy of the photon is zero.
holds for the photon, so that the invariant energy of the photon is zero.
In four-dimensional formalism in Minkowski space the
energy ![]() can be
calculated through the 4-momentum
can be
calculated through the 4-momentum
![]() of the
particle:
of the
particle:
![]() ,
,
where ![]() is the
metric tensor of the Minkowski space,
is the
metric tensor of the Minkowski space, ![]() is
4-velocity,
is
4-velocity,
 is the Lorentz factor.
is the Lorentz factor.
As a result, 4-momentum can be represented
using the invariant energy: [1]
![]() ,
,
where ![]() is the 3-vector of relativistic momentum.
is the 3-vector of relativistic momentum.
In the curved spacetime with the metric tensor ![]() the invariant energy of the particle is found as follows:
the invariant energy of the particle is found as follows:
![]() .
.
If we take into account the definition of 4-velocity: ![]() , where
, where ![]() is 4-displacement vector,
is 4-displacement vector, ![]() is the differential of the proper time; and the definition of the spacetime
interval:
is the differential of the proper time; and the definition of the spacetime
interval: ![]() , then again we obtain the
equality:
, then again we obtain the
equality: ![]() .
.
System of particles
In elementary particle physics interaction of several
particles, their coalescence and decay with formation of new particles are
often considered. Conservation of the sum of 4-momenta of free particles before
and after the reaction leads to the conservation laws of energy and momentum of
the system of particles under consideration. The invariant energy ![]() of the system of particles is calculated as their total relativistic energy
in the reference frame in which the center of momentum of the particle system is stationary. In this case
of the system of particles is calculated as their total relativistic energy
in the reference frame in which the center of momentum of the particle system is stationary. In this case ![]() can differ from the sum of invariant energies of the particles of the
system, since the contribution into
can differ from the sum of invariant energies of the particles of the
system, since the contribution into ![]() is made not only by the rest energies of the particles, but also by the
kinetic energies of the particles and their potential energy. [2] If we observe the particles before or after the
interaction at large distances from each other, when their mutual potential
energy can be neglected, the invariant energy of the system is defined as:
is made not only by the rest energies of the particles, but also by the
kinetic energies of the particles and their potential energy. [2] If we observe the particles before or after the
interaction at large distances from each other, when their mutual potential
energy can be neglected, the invariant energy of the system is defined as:
![]() ,
,
where ![]() is the sum of relativistic energies of the system’s particles,
is the sum of relativistic energies of the system’s particles, ![]() is the vector sum of the particles’ momenta.
is the vector sum of the particles’ momenta.
Massive body
General relativity
In determining the invariant energy of a
massive body in general
relativity (GR) there is a problem with the
contribution of gravitational field energy, [3] since
the stress-energy tensor of gravitational field is not clearly defined,
and stress-energy-momentum pseudotensor is
used instead. In case of asymptotically flat spacetime at infinity for estimation
of the invariant energy the ADM
formalism for mass-energy of the body can be applied. [4] For
stationary spacetime metric the Komar
mass and energy are determined. [5] There
are other approaches to determination of the mass-energy, such as Bondi
energy, [6] and Hawking energy.
In the weak-field approximation the
invariant energy of a stationary body in GR is estimated as follows: [7]
![]()
where the mass ![]() and charge
and charge ![]() of
body are obtained by integrating the corresponding density by volume,
of
body are obtained by integrating the corresponding density by volume, ![]() is
the energy of motion of particles inside the body,
is
the energy of motion of particles inside the body, ![]() is
the gravitational constant,
is
the gravitational constant, ![]() is
the radius of the body,
is
the radius of the body, ![]() is
the electric constant,
is
the electric constant, ![]() is
the pressure energy.
is
the pressure energy.
For the masses, the relation is:
![]()
where the inertial mass of the system ![]() is
equal to the gravitational mass
is
equal to the gravitational mass ![]() , the
mass
, the
mass ![]() denotes the total mass of the particles that compose the body.
denotes the total mass of the particles that compose the body.
Covariant theory of
gravitation
In covariant theory of gravitation (CTG) in
the calculation of the invariant energy the energy partition into 2 main parts
is used – for the components of the energy fields themselves and for components
associated with the energy of the particles in these fields. Calculation shows
that the sum of the components of the energy of acceleration field, pressure field, gravitational and
electromagnetic fields, for the spherical shape of the body is zero. [8]
As a result there is only a sum of the energies of the
particles in the four fields:
![]()
where ![]() is the Lorentz factor of particles, and
is the Lorentz factor of particles, and ![]() is the scalar potential of pressure field at
the surface of system.
is the scalar potential of pressure field at
the surface of system.
The ratio of the masses is as follows: ![]()
In this case the inertial mass system ![]() should be equal to the total mass of
particles
should be equal to the total mass of
particles ![]() , the mass
, the mass ![]() equals the gravitational mass
equals the gravitational mass ![]() and excess
and excess ![]() over
over ![]() is due to the fact that particles
move inside the body and are under pressure in the gravitational and
electromagnetic fields.
is due to the fact that particles
move inside the body and are under pressure in the gravitational and
electromagnetic fields.
A more accurate expression for the invariant energy is
presented in the following article: [9]
![]()
For the case of a relativistic uniform system,
the invariant energy can be expressed as: [10] [11]

This leads to a change in the ratio for the masses:
![]()
Here the gauge mass ![]() is related to the cosmological constant and
represents the mass-energy of the matter’s particles in the four-potentials of
the system’s fields;
is related to the cosmological constant and
represents the mass-energy of the matter’s particles in the four-potentials of
the system’s fields; ![]() is the inertial mass ; the auxiliary mass
is the inertial mass ; the auxiliary mass ![]() is equal to the product of the particles’
mass density by the volume of the system; the mass
is equal to the product of the particles’
mass density by the volume of the system; the mass ![]() is the sum of the invariant masses (rest
masses) of the system’s particles, which is equal in value to the gravitational
mass
is the sum of the invariant masses (rest
masses) of the system’s particles, which is equal in value to the gravitational
mass ![]() .
.
In Lorentz-invariant theory of gravitation (LITG),
in which CTG is transformed in the weak-field approximation and at a constant
velocity of motion, for the invariant energy the following formula holds:
![]() ,
,
where ![]() is
the relativistic energy of a moving body taking into account the contribution
of the gravitational and electromagnetic field energy,
is
the relativistic energy of a moving body taking into account the contribution
of the gravitational and electromagnetic field energy, ![]() is
the total momentum of the system.
is
the total momentum of the system.
These formulas remain valid at the atomic level, with the difference
that the usual gravity replaced by strong gravitation. In the
covariant theory of gravitation based on the principle of least action is shown
that the gravitational mass ![]() of
the system increases due to the contribution of mass-energy of the
gravitational field, and decreases due to the contribution of
the electromagnetic mass-energy. This is the consequence of the fact that in
LITG and in CTG the gravitational stress-energy tensor is
accurately determined, which is one of the sources for the determining the
metric, energy and the equations of motion of matter and field. The acceleration stress-energy tensor, dissipation stress-energy tensor and
pressure
stress-energy tensor are also identified in
covariant form.
of
the system increases due to the contribution of mass-energy of the
gravitational field, and decreases due to the contribution of
the electromagnetic mass-energy. This is the consequence of the fact that in
LITG and in CTG the gravitational stress-energy tensor is
accurately determined, which is one of the sources for the determining the
metric, energy and the equations of motion of matter and field. The acceleration stress-energy tensor, dissipation stress-energy tensor and
pressure
stress-energy tensor are also identified in
covariant form.
Vector fields such as the gravitational
and electromagnetic fields, the acceleration field,
the pressure field,
the dissipation field,
the fields of strong and weak interactions are components of general field.
This leads to the fact that the invariant energy of the system of particles and
fields can be calculated as the volumetric
integral in the center-of-momentum
frame: [12]
![]()
where ![]() and
and ![]() denote the time components of the
4-potential
denote the time components of the
4-potential ![]() of general field and the mass 4-current
of general field and the mass 4-current ![]() ,
respectively,
,
respectively, ![]() is the tensor of the general field.
is the tensor of the general field.
In general, the energy of a
system taking into account four vector fields is calculated using the
formula: [13]
![]()
![]()
![]()
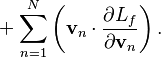
Here ![]() are the scalar
potentials of electromagnetic and gravitational fields, acceleration field, and
pressure field, respectively;
are the scalar
potentials of electromagnetic and gravitational fields, acceleration field, and
pressure field, respectively; ![]() denote the
vector potentials of the fields;
denote the
vector potentials of the fields; ![]() are the
tensors of these fields;
are the
tensors of these fields; ![]() is the part of the Lagrangian function associated with tensor
invariants;
is the part of the Lagrangian function associated with tensor
invariants; ![]() denotes the
velocity of the particles in the system.
denotes the
velocity of the particles in the system.
In the case where all
quantities in the presented formula for energy are calculated in the reference
frame associated with the center of momentum of the system, invariant energy is
obtained.
See also
- Invariant mass
- Principle of energies summation
- Field mass-energy limit
- General
field
- Dissipation field
- Acceleration
field
- Pressure
field
- Field energy theorem
References
- McGlinn,
William D. (2004), Introduction to relativity, JHU
Press, ISBN 0-8018-7047-X, Extract
of page 43.
- Landau L.D.,
Lifshitz E.M. (1975). The Classical Theory of Fields. Vol. 2 (4th ed.).
Butterworth-Heinemann. ISBN 978-0-750-62768-9.
- Misner,
Charles W.; Kip. S. Thorne & John A. Wheeler (1973), Gravitation, W.
H. Freeman, ISBN 0-7167-0344-0
- Arnowitt, Richard;
Stanley Deser & Charles W. Misner (1962), "The dynamics of
general relativity", in Witten, L., Gravitation: An Introduction to
Current Research, Wiley, pp. 227-265.
- Komar, Arthur
(1959). "Covariant Conservation Laws in General Relativity".
Phys. Rev. 113 (3): 934–936. Bibcode 1959PhRv..113..934K.
doi:10.1103/PhysRev.113.934
- Bondi H, van
de Burg M G J, and Metzner A W K, Proc. R. Soc. London
Ser. A 269:21-52 Gravitational waves in General Relativity. VII. Waves
from axi-symmetric isolated systems (1962).
- V. A. Fock, The Theory of Space, Time and
Gravitation (Pergamon Press, London, 1959).
- Fedosin S.G. Relativistic
Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8 (No. 1), pp. 1-16, (2015).
- Fedosin S.G. The generalized Poynting theorem for
the general field and solution of the 4/3 problem. International Frontier
Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
- Fedosin S.G. The binding energy and the total
energy of a macroscopic body in the relativistic uniform model. Middle
East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
- Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
- Fedosin S.G. The Concept of the General
Force Vector Field. OALib Journal, Vol. 3, P. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
- Fedosin S.G. What should we understand by the
four-momentum of physical system? Physica Scripta, Vol. 99, No. 5,
055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.