На русском языке

Principle of energies summation

Principle of energies summation of an arbitrary system sets the order of inclusion of various types of energy, associated with the system, into energy functions that describe the state of the system. Energy summation is most frequently used in theoretical physics, where principle of least action is used, total energy of systems is calculated and the law of energy conservation is taken into account. Principle of energies summation on the one hand is a methodological principle, but on the other hand – is result of complexity of systems, consisting of matter in different states, and of fields available in these systems. The complexity increases due to motion of matter and fields during transitions of matter from one phase state to another, and during transformation of energies of fields and matter into each other. Energy functions have different meaning depending on their purpose. To estimate change in energy of a system we need to take into account that some components increase energy, and others reduce it, which leads to different signs before energy components. If energy functions are used to find equations of motion, the signs before the energy components are chosen according to condition of conforming to the equations of motion of matter and fields. As a result, for each energy function its own order of energies summation is used.

Contents

  • 1 Examples
    • 1.1 Thermodynamic potentials
    • 1.2 Lagrangian
    • 1.3 Hamiltonian
    • 1.4 Invariant energy
    • 1.5 Relativistic energy
    • 1.6 Equations for metric

o         1.6.1 Einstein-Hilbert equations

o         1.6.2 Equations of CTG

  • 2 References
  • 3 See also
  • 4 External links

Examples

Thermodynamic potentials

To calculate the energy functions in thermodynamics such physical quantities are used as pressure ~P, volume ~V, absolute temperature ~T, heat capacity ~C, mass ~M,  amount of substance ~N. These quantities can be well measured, in contrast to entropy ~S, chemical potential  ~\mu , amount of heat ~Q, which are characteristic of substance. Internal energy ~U and its increment ~dU for multiphase substance in a quasi-static process are given by:

~U= \int ( T dS - P dV + \sum_i \mu_i dN_i + \delta A'),

~dU= \delta Q - \delta A + \sum_i \mu_i dN_i + \delta A' ,

where ~ \delta Q= T dS   is the increment of the amount of heat, ~ \delta A= P dV   is the work done by the system, ~ i   is the number of substance phases, ~ \delta A'   is the work done on the system.

Besides the internal energy in thermodynamics there are other energy functions associated with it, such as Helmholtz free energy:

~ \mathcal F = U - TS.

Accordingly, the increment of the Helmholtz free energy is:

~d \mathcal F = - S dT - \delta A + \sum_i \mu_i dN_i + \delta A' .

Enthalpy and its increment are as follows:

~H=U+PV,

~dH= \delta Q + V dP + \sum_i \mu_i dN_i + \delta A' .

Gibbs free energy and its increment are:

~G=U+PV-TS,

~dG= -S dT + V dP + \sum_i \mu_i dN_i + \delta A' .

Grand thermodynamic potential and its increment are:

~\Omega = U - TS - \sum_i \mu_i N_i ,

~d \Omega = - S dT - \delta A - \sum_i N_i d\mu_i + \delta A' .

Bound energy and its increment are:

~E_b = U + PV - \sum_i \mu_i N_i ,

~d E_b = \delta Q +V dP - \sum_i N_i d\mu_i + \delta A' .

Two thermodynamic potentials and their increments are also possible:

~P_1 = U - \sum_i \mu_i N_i ,

~d P_1 = \delta Q - \delta A - \sum_i N_i d\mu_i + \delta A' ,

~P_2 = U - TS + PV - \sum_i \mu_i N_i ,

~d P_2 = - S dT +V dP - \sum_i N_i d\mu_i + \delta A' .

The order of addition of energy components is of such kind that we obtain corresponding thermodynamic potential, which has its own meaning. Thus, internal energy reflects the law of energy conservation, and change in Helmholtz free energy in an isothermal process is determined only by difference in work done by the system on environment and by the environment on the system.

Many relations of thermodynamics hold well not only for gas, but also for fluids and substance in solid state.

Lagrangian

One of the ways to find equations of motion of systems and laws of their existence is variation of the action functional, that is, variation by different variables of the time integral of Lagrangian, in order to determine the extreme and most probable states. Lagrangian  ~L  consists of several energy components, which in mechanics are either part of kinetic energy ~ T  or of potential energy ~ V . In order to find the Lagrangian in mechanics the difference between kinetic and potential energies is written as follows:

L=T-V.

It is generally assumed that Lagrangian depends only on time, coordinates and velocities, but does not depend on the higher time derivatives.

Since matter in each mechanical system is a source of its own fields, then in expression for Lagrangian in general case, terms associated with energies of these fields are added. In special relativity, Lagrangian of a particle with mass ~M  and charge ~ q   in electromagnetic field has the following form: [1]

~L=-Mc{\frac {ds}{dt}}-q{\frac {A_{\mu }dx^{\mu }}{dt}}-{\frac {c\varepsilon _{0}}{4}}\int {F_{{\mu \nu }}F^{{\mu \nu }}{\frac {dx^{4}}{dt}}}=

= - Mc^2 \sqrt {1-v^2/c^2} -q(\varphi- \mathbf {A \cdot v}) + \frac {\varepsilon_0}{2} \int {(E^2 -c^2 B^2)} dx^3 ,

where ~c  is speed of light, ~ds  is spacetime interval, ~ A_\mu = \left( \frac {\varphi }{c},-\mathbf {A}\right)   is electromagnetic 4-potential with lower (covariant) index, ~ dx^\mu   is 4-displacement vector of particle, ~ \varepsilon_0  is electric constant, ~ F_{\mu \nu}   is electromagnetic field tensor, ~ dx^4 =c dtdx^3 =c dtdx{}dy{}dz   is 4-volume, ~ \mathbf {v}  is velocity of the particle, ~ \varphi  and ~ \mathbf {A}  are scalar and vector potentials of electromagnetic field, respectively, ~ E  and ~B  are electric field strength and magnetic induction, respectively.

In this case, the Lagrangian includes three components with dimension of energy, which are associated with relativistic energy of the particle, with energy of the particle in electromagnetic field, and with electromagnetic field energy. The expressions for energy components and the signs before them are chosen so that by varying the action functional we would obtain equations of particle’s motion in the field and Maxwell's Equations for field strengths.

Similarly, Lagrangian is written for a single particle in gravitational field in Lorentz-invariant theory of gravitation: [2]

~L=-Mc{\frac {ds}{dt}}-M{\frac {D_{\mu }dx^{\mu }}{dt}}+{\frac {c}{16\pi G}}\int {\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}{\frac {dx^{4}}{dt}}}=

=-Mc^{2}{\sqrt {1-v^{2}/c^{2}}}-M(\psi -{\mathbf {D\cdot v}})-{\frac {1}{8\pi G}}\int {(\Gamma ^{2}-c^{2}\Omega ^{2})}dx^{3}

where  ~D_{\mu }=\left({\frac {\psi }{c}},-{\mathbf {D}}\right)  is gravitational four-potential with lower (covariant) index, ~ G   is the gravitational constant, ~ \Phi_{\mu \nu}   is gravitational tensor, ~ \psi   and ~ \mathbf {D}  are scalar and vector potentials of gravitational field, respectively, ~ \Gamma  and  ~\Omega   are gravitational field strength and gravitational torsion field, respectively, and mass  ~ M   not only takes into account sum of nucleons masses of matter, but also contribution of mass-energy of fields interacting with matter and changing particle mass.

After varying the action functional we obtain equations of motion of particle in gravitational field and Maxwell-like gravitational equations for gravitational field strength and torsion field. To use the Lagrangian in any frames of reference, it should be written in covariant form. In curved spacetime interval can be expressed using metric tensor  ~ g_{\mu\nu} :

~ds = \sqrt {g_{\mu\nu}\ dx^{\mu} \ dx^{\nu}},

and instead of component of 4-volume ~ dx^4   during integration over the 4-volume we should use the product ~ \sqrt {-g}dx^4 , where ~ g   is determinant of metric tensor.

Hamiltonian

In classical mechanics, Hamiltonian of system of particles can be defined with the Lagrangian: ~H=\sum _{i}{{\vec p}_{i}}\cdot {\dot {{\vec q}_{i}}}-L ,

where ~\vec p_i  is generalized momentum of i-th particle, and ~\dot {\vec q_i}  is its generalized velocity.

For conservative systems in which the energy is conserved, the Hamiltonian as a function of generalized coordinates and momenta is equal to the total energy ~ E   of the system and has the following form:

H=E = T + V .

In this case, we see that distinction between Lagrangian and Hamiltonian is in different signs before potential energy ~ V   of the system.

Invariant energy

Invariant energy ~E_0  of a body is defined as relativistic energy, measured by an observer who is fixed relative to the body’s center of momentum. Standard approach involves summation of all types of energy of the body:

~E_0= E_m + E_p + E_T + U +W+ E_L ,

where ~E_m   is rest energy of individual matter particles, ~E_p   is pressure (compression) energy of matter understood as potential energy of interatomic interactions, ~E_T   is thermal energy, which being summed with ~E_p   yields internal energy, ~ U   is gravitational energy of the body, including energy of proper field in the body matter and beyond it and gravitational energy in field from external sources, ~ W   is electromagnetic energy of the body, ~ E_L   is energy of radiation interacting with the body matter.

In general relativity this leads to the fact that a heated body should increase its mass, and the mass of a gravitationally bound body should be less than total mass of particles of matter that forms this body.

There is an alternative point of view that energy components are included in equation for invariant energy with negative signs: [3] [4] [5]  [6]  [7]

~E_0= E_m - E_p - E_T - U -W- E_L .

As a result, heated bodies should have less mass than cold, and mass of a star must be greater than the mass of scattered matter from of which it was made up during gravitational collapse.

The third approach involves rethinking the nature and order of summation energies in covariant theory of gravitation (CTG). Method of calculating invariant energy depends essentially on how to account for scalar curvature and cosmological constant in energy. In particular, the cosmological constant can be calibrated in such a way as to exclude the scalar curvature, and thus find a unique expression for the energy. [8] Another innovation is that instead of standard stress-energy tensor of matter, taking into account inner pressure, in consideration introduces two new vector fields –acceleration field and pressure field, with corresponding stress-energy tensors. If we add electromagnetic and gravitational fields, then obtained four fields symmetrically involved in Lagrangian and energy. Calculation of invariant energy in spherical body shows that components of energy of all four fields cancel each other. Therefore contribution to invariant energy of system makes only potential energies of particles which are under influence of fields. [9] These energies are also partially reduced, and for invariant energy can be written:

~E_{0}= Mc^2=m_b c^2 - \frac {3G m^2_b}{10a}+ \frac {3 q^2_b}{40 \pi \varepsilon_0 a}.

Relation for mass is as follows: ~m' = M < m_ b = m_g,

where mass {\displaystyle ~m_{b}} and charge {\displaystyle ~q_{b}} are calculated by integrating corresponding density by volume of the body with radius {\displaystyle ~a} , system mass {\displaystyle ~M} equals total mass of particles {\displaystyle ~m'}, mass {\displaystyle ~m_{b}} equals gravitational mass {\displaystyle ~m_{g}} , and excess {\displaystyle ~m_{b}}  over {\displaystyle ~M}  is due to the fact that particles move inside the body and are under pressure in gravitational and electromagnetic fields.

A more accurate expression is presented in following articles, [10] [11] where for energy and mass there is the following:

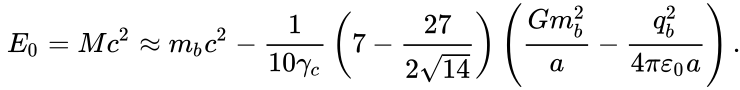
{\displaystyle ~E_{0}=Mc^{2}\approx m_{b}c^{2}-{\frac {1}{10\gamma _{c}}}\left(7-{\frac {27}{2{\sqrt {14}}}}\right)\left({\frac {Gm_{b}^{2}}{a}}-{\frac {q_{b}^{2}}{4\pi \varepsilon _{0}a}}\right).}

 

{\displaystyle ~m'<M<m<m_{b}=m_{g}.}

Here gauge mass {\displaystyle ~m'} is related to cosmological constant and represents mass-energy of matter’s particles in four-potentials of the system’s fields; {\displaystyle ~M} is inertial mass; auxiliary mass {\displaystyle ~m}  is equal to the product of particles’ mass density by volume of the system; mass {\displaystyle ~m_{b}}  is sum of invariant masses (rest masses) of the system’s particles, which is equal in value to gravitational mass {\displaystyle ~m_{g}}.

Relativistic energy

In contrast to invariant energy, relativistic energy generally includes additional energy components associated with the motion of the system as a whole. As a result, in formulas for the energy dependence on velocity can be determined, such as on the velocity ~v of the center of momentum of the system. If in Minkowski space invariant energy ~E_0  is known, then the relativistic energy in an arbitrary inertial reference frame is found using the Lorentz transformation by the following formula:

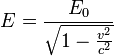~E= \frac {E_0} {\sqrt {1-\frac {v^2}{c^2}} } .

For continuously distributed matter in curved space-time, expression for energy of a physical system has the following form:[12]

 

~E=\int \left[{\mathbf v}\cdot {\frac {\partial }{\partial {\mathbf v}}}\left({\frac {{\mathcal {L}}_{p}}{u^{0}}}\right)u^{0}-{\mathcal {L}}_{p}\right]{\sqrt {-g}}dx^{1}dx^{2}dx^{3}-\int {\mathcal {L}}_{f}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+\sum _{{n=1}}^{N}\left({\mathbf v}_{n}\cdot {\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right).

 

In this expression, Lagrangian density of the system ~{\mathcal {L}} is presented as sum of two parts ~{\mathcal {L}}={\mathcal {L}}_{p}+{\mathcal {L}}_{f}, where ~{\mathcal {L}}_{p} depends on four-potentials and four-currents, and ~{\mathcal {L}}_{f} contains tensor invariants of fields. The quantity ~L_{f}=\int {\mathcal {L}}_{f}{\sqrt {-g}}dx^{1}dx^{2}dx^{3} is that part of Lagrangian which is obtained by integrating ~{\mathcal {L}}_{f} over moving volume of the physical system. In matter of the system velocity of particles is ~{\mathbf v}, the quantity ~u^{0} is time component of four-velocity of these particles, ~g is determinant of metric tensor. When calculating contribution of particle fields to energy of the system it is necessary to divide matter into ~N particles or elements of matter of point sizes. Each such particle has some velocity ~{\mathbf v}_{n}, while ~L_{f} and energy of the system ~E in general case depend on the velocities ~{\mathbf v}_{n}.

For four vector fields, the energy is expressed through scalar potentials of fields ~\varphi ,\psi ,\vartheta ,\wp , through vector potentials of the fields ~{\mathbf A},{\mathbf D},{\mathbf U},{\mathbf \Pi }, and through tensors of the fields ~F_{{\mu \nu }},\Phi _{{\mu \nu }},u_{{\mu \nu }},f_{{\mu \nu }}:

 

 

Equations for metric

Einstein-Hilbert equations

Einstein-Hilbert equations of general relativity (GR) are aimed to find metric in curved spacetime and are written in tensor form:

R_{\mu\nu } - {R \over 2} g_{\mu\nu } + \Lambda g_{\mu\nu } = {8 \pi \beta G \over c^4} T_{\mu\nu },

where ~R_{\mu\nu } is Ricci curvature tensor, ~R   is scalar curvature, ~\Lambda  is cosmological constant, and ~T_{\mu\nu }  is a stress-energy tensor with dimension of volumetric energy density, ~G   is Newton's gravitational constant.

In GR ~\beta=1   and tensor ~T_{\mu\nu }  usually includes stress-energy tensor of matter ~ \phi_{\mu\nu }  and stress-energy tensor of electromagnetic field ~ W_{\mu\nu }:

~ T_{\mu\nu} = \phi_{\mu\nu }+ W_{\mu\nu } .

Absence of stress-energy tensor of gravitational field as a source affecting the metric in GR is due to the fact that gravitational field is identified with geometrical field in the form of metric field, and this field does not generate itself (absence of self-action of the metric field).

Equations of CTG

In covariant theory of gravitation (CTG) equations for metric are as follows: [8] [13]

R_{\mu\nu } - {R \over 4} g_{\mu\nu } = {8 \pi \beta G \over c^4} T_{\mu\nu },

where the coefficient ~\beta   is found from equations of motion of particles and waves in any given form of metric, and the tensor ~T_{\mu\nu }  is sum of four tensors:

~ T_{\mu\nu} = B_{\mu\nu }+ W_{\mu\nu } + U_{\mu\nu } + P_{\mu\nu },

 

where  ~ U_{\mu\nu }   is stress-energy tensor of gravitational field, ~ B_{\mu\nu }   is acceleration stress-energy tensor, and  ~ P_{\mu\nu }   is pressure stress-energy tensor.

This means that in CTG gravitational field is a physical field and along with electromagnetic field, acceleration field and pressure field it is the source forming spacetime metric.

For the case of continuously distributed matter we obtain equality for cosmological constant:

 

~\Lambda ={16\pi \beta G \over c^{4}}(D_{\kappa }J^{\kappa }+A_{\kappa }j^{\kappa }+U_{\kappa }J^{\kappa }+\pi _{\kappa }J^{\kappa }),

 

where ~ J^\kappa   and  ~ j ^\kappa  are the mass and electromagnetic 4-currents, respectively, ~U_{\kappa }  and  ~ \pi_\kappa  – 4-potentials of acceleration field and pressure field.

The covariant derivative of the left side of equation for metric due to calibration of cosmological constant and scalar curvature is zero. This allows us to write equation of matter motion as equality to zero of covariant derivative of sum of the tensors in the right side, taken with contravariant indices:

~ \nabla_\nu ( B^{\mu\nu }+ W^{\mu\nu } + U^{\mu\nu } + P^{\mu\nu } )=0 .

 

General field

In concept of general field it is assumed that all vector fields associated with matter are components of this field. 4-potential of general field   ~ s_\mu   is sum of 4-potentials of particular fields. [14] [15]  As a result, the sum of terms in Lagrangian responsible for energy of matter in various fields, up to a sign is simply the product of   ~ s_\mu J^\mu . As for the energy of particular fields themselves, these energies are included in Lagrangian through the general field tensor  ~ s_{\mu \nu} , obtained as 4-curl of the 4-potential of general field. For Lagrangian we obtain the relation:

~L=\int (kcR-2kc\Lambda -s_{\mu }J^{\mu }-{\frac {c^{2}}{16\pi \varpi }}s_{{\mu \nu }}s^{{\mu \nu }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3},

where ~k   and  ~ \varpi   are the constants to be determined; ~ \sqrt {-g} dx^1 dx^2 dx^3  is invariant 3-volume expressed in terms of product  ~ dx^1 dx^2 dx^3   of space coordinates’ differentials and square root  ~\sqrt {-g}   of determinant  ~g   of metric tensor, taken with a negative sign.

The relativistic energy of the system is:

~E = \int {( s_0 J^0 + \frac {c^2 }{16 \pi \varpi } s_{ \mu\nu} s^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},

 

where ~ s_0   and  ~ J^0  denote the time components of the 4-vectors  ~ s_{\mu }   and  ~ J^{\mu } .

 

The feature of expression for energy is that in it general field energy in the tensor product   ~ s_{\mu \nu} s^{\mu \nu}  includes not only energies of particular fields, but also cross-terms in the form of a sum of products of particular fields strengths in various combinations. We can say that the energy of particles in particular fields is included in energy of the system linearly, and the energy fields themselves – approximately quadratically.

References

  1. Landau L.D., Lifshitz E.M. (1975). The Classical Theory of Fields. Vol. 2 (4th ed.). Butterworth-Heinemann. ISBN 978-0-750-62768-9.
  2. Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1.
  3. Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body. Preprints 2017, 2017040150. http://dx.doi.org/10.20944/preprints201704.0150.v1.
  4. Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of Gravitomagnetic Theory. Canadian Journal of Physics, Vol. 92, No. 10, pp. 1074-1081 (2014). http://dx.doi.org/10.1139/cjp-2013-0683.
  5. Fedosin S.G. The Principle of Proportionality of Mass and Energy: New Version. Caspian Journal of Applied Sciences Research, Vol. 1, No. 13, pp. 1-15 (2012). http://dx.doi.org/10.5281/zenodo.890753.
  6. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.
  7. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023.
  8. 8.0 8.1 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
  9. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210.
  10. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
  11. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
  12. Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?
  13. Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских векторных полей.
  14. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
  15. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025. // Две компоненты макроскопического общего поля.

See also

External links

 

Source: http://sergf.ru/pseen.htm

On the list of pages