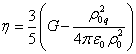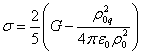Bulletin of Pure and Applied Sciences, Vol.38 D (Physics), No. 2, pp.
73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5
Иерархия масс в релятивистской
однородной системе
Федосин Сергей Григорьевич
ул. Свиязева 22-79,
город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Анализ релятивистской однородной
системы в рамках ковариантной теории гравитации приводит к пяти различным массам физической
системы, в которой частицы связаны друг с другом посредством
электромагнитного и гравитационного полей, поля ускорений и поля давления. При этом оказывается, что
гравитационная масса системы равна сумме инвариантных масс всех частиц системы,
а инертная масса системы меньше гравитационной
массы на величину массы-энергии связи системы.
Ключевые слова: релятивистская однородная система; гравитационная масса; инертная масса; энергия
системы.
The mass hierarchy in the relativistic
uniform system
Sergey G. Fedosin
PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia
E-mail: fedosin@hotmail.com
The analysis of the relativistic uniform system in the framework of the
covariant theory of gravitation leads to five different masses of the physical
system, in which the particles are bound together by means of the
electromagnetic and gravitational fields, the acceleration field and the
pressure field. In this case it turns out that the system’s gravitational mass
is equal to the sum of the invariant masses of all the system’s particles, and the
system’s inertial mass is less than the gravitational mass by the value of the
system’s binding mass-energy.
Keywords: relativistic uniform system;
gravitational mass; inertial mass; energy of system.
1. Введение
Для каждой физической системы можно
ввести несколько типов масс, каждая из которых по-своему характеризует систему.
Широко известна инертная или инвариантная масса, связанная с релятивистской
энергией системы множителем в виде фактора Лоренца и квадрата скорости света.
Если выбранная система отсчёта неподвижна относительно центра импульсов
рассматриваемой физической системы, фактор Лоренца системы становится равным
единице. В такой системе отсчёта остаётся ещё собственное движение частиц и
полей, и необходимо учитывать факторы Лоренца отдельных частиц. При вычислении
релятивисткой энергии оказывается, что вклад в инертную массу делают как
энергии частиц в действующих на них полях, так и энергии самих полей. В
частности, энергия гравитационного и электромагнитного полей должна вычисляться
и в пустом пространстве между частицами и даже за пределами системы. Более
того, частицы вещества, включая малые частицы с размерами отдельного атома, содержат
в себе почти одну пустоту. Это связано с тем, что почти вся масса атома
содержится в небольшом по размерам атомном ядре. Поэтому энергия поля должна
вычисляться ещё и внутри частиц вещества. В связи с этим при вычислении энергии
поля как правило производят интегрирование по всему объёму пространства
используемой системы отсчёта.
В классической механике инертная масса связана
не только с релятивисткой энергией, но и определяет ускорение тел под действием
приложенных к системе сил. Некоторым исключением является сила гравитации.
Можно считать, что гравитационная сила, действующая со стороны тела 1 на тело
2, пропорциональна активной гравитационной массе тела 1 и пассивной
гравитационной массе тела 2. Указанные массы трактуются по-разному в
зависимости от используемой теории гравитации. Например, в общей теории
относительности активная и пассивная гравитационные массы не отличаются друг от
друга, а инертная масса равна гравитационной массе системы.
Существует по крайней мере ещё одна
масса, часто применяемая в астрофизике. Это суммарная масса барионов,
составляющих систему, к которой для точности добавляют ещё суммарную массу
имеющихся электронов. Действительно, вещество планет и звёзд состоит из
нуклонов и электронов, которые могут соединяться друг с другом, образуя
отдельные атомные ядра, атомы и ионы, а также вещество в различных фазовых
состояниях. Очевидно, что суммарная масса барионов и электронов не равна
инертной массе системы, поскольку при образовании связанной системы из неё
выделяется энергия связи и релятивистская энергия системы уменьшается.
Далее мы рассмотрим вопрос о том, каким
образом связаны между собой вышеуказанные массы в ковариантной теории
гравитации. При этом мы будем использовать физическую модель из частиц и полей,
представляющую собой релятивистскую однородную систему. С целью упрощения в
расчёт будут приняты только основные четыре поля, включая электромагнитное и
гравитационное поля, поле ускорений и поле давлений. Каждое из этих полей
предполагается векторным полем максвелловского типа. Все эти поля
рассматриваются как соответствующие компоненты общего поля [1], [2], и
используются для описания макроскопических систем [3].
Указанный подход был использован ранее
для оценки различных масс системы из частиц и полей сферической формы в [4],
[5]. В рассматриваемой системе частицы движутся хаотически и настолько тесно
друг к другу, что применимо приближение непрерывного распределения вещества.
При этом часть частиц заряжена, а распределение плотности заряда подобно
распределению плотности массы.
Используя теперь свойства
релятивистской однородной системы [6], мы вычислим более точные значения масс
системы и сравним их, расположив в определённой последовательности. Исходной
точкой наших рассуждений будет формула для релятивистской энергии физической
системы с непрерывным распределением вещества [7] :
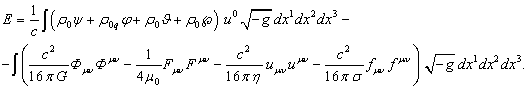(1)
В (1) 
есть скорость света; 
и 
обозначают инвариантные плотности массы и
заряда соответственно; 
, 
, 
и 
– скалярные потенциалы гравитационного и
электромагнитного полей, поля ускорений и поля давления, соответственно;
, 
, 
и 
– тензоры этих полей, соответственно; 
– временная компонента 4-скорости
элемента вещества; 
– детерминант метрического тензора; 
– произведение дифференциалов
пространственных координат; 
– гравитационная постоянная; 
– магнитная постоянная; 
– постоянная поля ускорений; 
– постоянная поля давления.
Формула (1) справедлива в приближении,
в котором потенциалы и тензоры полей, находимые как суперпозиции вкладов всего
множества частиц, не зависят от скоростей движения отдельных частиц системы. С
помощью этой формулы в [5] энергия для равновесной
системы сферической формы с непрерывно распределённым хаотически движущимся веществом
с учётом энергии полей была вычислена в явном виде с точностью до членов, не
содержащих в знаменателях квадрат скорости света. С учётом поправок, сделанных
в [8], энергия равна [9]:
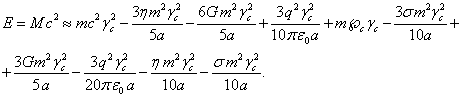(2)
Последние 4 члена в (2) задают энергии
полей, величина 
есть инвариантная
инертная масса системы, масса 
определяется через
произведение плотности массы на объём сферы с
веществом, 
есть фактор Лоренца
движения частиц в центре сферы, 
обозначает радиус
сферы, заряд 
определяется через
произведение плотности заряда на объём сферы,
– электрическая
постоянная, 
– скалярный потенциал поля давления в
центре сферы.
2. Нормировка массы и энергии
Энергия системы является интегральной
величиной, содержит вклады от энергии частиц и полей и в общем случае требует
нормировки. Удобно нормировать энергию с помощью космологической постоянной 
, входящей в лагранжиан системы. Формула (1) для четырёх основных полей получена
при следующем условии [7]:
, (3)
где 
– 4-потенциал
гравитационного поля в рамках ковариантной теории гравитации,
– массовый 4-ток,
– плотность массы в
сопутствующей частице системе отсчёта,
– 4-скорость точечной
частицы,
– 4-потенциал
электромагнитного поля,
–
зарядовый 4-ток,
– плотность заряда в сопутствующей частице системе отсчёта,
– 4-потенциал поля
ускорений,
– 4-потенциал поля
давления,
, 
, 
и 
являются векторными
потенциалами гравитационного и электромагнитного полей, поля ускорений и поля
давления, соответственно.
С помощью (3)
осуществляется упрощение уравнения для метрики и калибровка релятивистской
энергии таким образом, что из них исчезает как 
, так и скалярная кривизна 
.
В пределе специальной теории
относительности 4-токи равны:
, 
, где 
есть фактор Лоренца, 
– скорость частиц
вещества. Подставим это в (3):
. (4)
В пределе
малых скоростей можно пренебречь членами, содержащими скорость 
частиц и векторные
потенциалы. Тогда в (4) фактор Лоренца 
и остаются только
члены со скалярными потенциалами полей. Для рассеянных на бесконечности в
космическом пространстве частиц можно считать, что эти потенциалы возникают
только от собственных полей частиц и являются усреднёнными потенциалами по
объёму частиц. В этом случае 
и можно записать:
. (5)
Скалярные
потенциалы полей внутри сферы были найдены в [10]. После
упрощения они выглядят так:
, 
,
, 
.
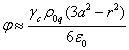Отсюда видно,
что космологическая постоянная определяется плотностью энергии покоя частиц с
добавкой от плотности энергии частиц в собственных полях. Если (5) усреднить по
космическому пространству, то при 
, где 
есть константа порядка
единицы, получается значение 
. Подставляя сюда стандартную оценку космологической
постоянной 
м–2, находим соответствующую плотность вещества: 
кг/м, что
достаточно близко к наблюдаемой средней плотности массы материи.
Предположим
теперь, что некоторое количество вещества под действием гравитации собирается в
такие объекты, как газовые облака, а затем и в планеты и звёзды. В [5] мы интегрировали (4) по объёму неподвижной сферы,
заполненной частицами, которые удерживались в этом состоянии благодаря действию
гравитации и электромагнитного поля, с учётом внутреннего поля ускорений и поля
давления. Если обозначить через 
калибровочную
массу-энергию частиц системы, связанную с космологической постоянной в левой
части (4), то с учётом полученного в [8, 9] более точного значения энергий
частиц в потенциалах гравитационного и электромагнитного полей, для результата
интегрирования получается следующее:
. (6)
Члены в правой
части (6) содержатся в (2), так что энергию можно записать в следующем виде:
.
(7)
В (2) используются масса 
и заряд 
, как вспомогательные величины. Однако за пределами сферы
потенциалы гравитационного и электромагнитного поля определяются с помощью
массы 
и электрического
заряда 
. Для этих масс и зарядов получается [5], [11]:
, 
.
(8)
Уравнение движения
вещества внутри сферы [3] и обобщённая теорема Пойнтинга [9] приводят к
следующему соотношению между коэффициентами полей:
.
(9)
С учётом (8)
и (9) энергию (7) можно переписать так:
Отсюда видно, что релятивистская
энергия системы равна суммарной энергии частиц в собственных полях, из которой
следует ещё вычесть энергию гравитационного и электромагнитного поля за
пределами объёма, заполненного частицами системы.
3. Сравнение масс
В [12] была вычислена суммарная энергия
покоя 
частиц сферы с точки
зрения связанного со сферой наблюдателя, кинетическая энергия 
, скалярный потенциал 
поля давления в центре
сферы, найдены соотношения между коэффициентами полей и фактор Лоренца 
для движения частиц в
центре сферы:
, 
,
, 
, 
,
.
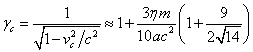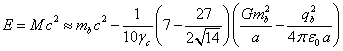(11)
В (11) энергия 
выражена через массу 
и заряд . Из сравнения (8), (10) и (11) вытекают соотношения для
масс-энергий рассматриваемой системы:
, (12)
, 
.
.
(13)
В (12) масса-энергия гравитационного и
электромагнитного полей за пределами вещества равна 
. Разница масс в (12) и (13) выражена в единицах
величины 
и может быть также
выражена через 
.
В (13) масса 
, носящая вспомогательный характер, равна произведению
плотности 
на объём тела, причём плотность 
измеряется в сопутствующих частицам системах
отсчёта. Калибровочная масса 
соотносится с массой-энергией частиц,
находящихся под воздействием полей, и связана с калибровкой энергии и с
космологической постоянной. Масса 
является инвариантной массой системы при
преобразованиях Лоренца и может считаться инертной массой. Масса 
больше других масс потому, что частицы внутри
сферы под действием полей двигаются быстрее и имеют увеличенный фактор Лоренца [5]. При этом масса как суммарная масса покоя частиц оказывается
равной гравитационной массе 
,
поскольку именно масса присутствует в выражениях для напряжённости,
скалярного потенциала и энергии гравитационного поля за пределами сферы [8].
В [12] было показано, что
.
(14)
Это означает, что энергия связи 
системы, делённая на
квадрат скорости света, с учётом соотношения 
,
есть разница между гравитационной массой 
и инвариантной массой 
рассматриваемой системы.
Поскольку в (12) масса предполагается
постоянной,
возможен случай, когда добавление электрического заряда к однородно заряженному
телу начинает уменьшать массу .
Хотя перенос заряда на тело увеличивает массу за счёт массы 
носителей заряда, но энергия электрического
поля растёт квадратично относительно заряда ,
и вклад массы-энергии поля может превысить вклад от .
Для этого должно выполняться условие:
.
Если 
, 
,
где 
и 
обозначают заряд и массу одного электрона, 
есть число перенесённых на тело электронов, то
это условие можно переписать как соотношение для электрического потенциала,
которое должно быть на поверхности тела:
, 
В.
В разделе 2 мы описываем калибровочную
массу , а в разделе 3 рассматриваем различные массы,
характеризующие систему, и выражаем их связь друг с другом. В (11)
релятивистская энергия представлена через массу 
и заряд системы 
.
а в (7) и (10) – через массу .
Калибровочная масса связана с энергией частиц в потенциалах всех
четырёх полей и выражается в (6).
Отличие от инвариантной
инертной массы системы в (2) заключается в том, что масса согласно (12) дополнительно содержит взятый с
обратным знаком вклад массы-энергии от электромагнитного и гравитационного
полей во всём объёме за пределами вещества. Массы-энергии полей внутри
рассматриваемой системы не делают никакого вклада, поскольку внутри сферы
действуют ещё поле ускорений и поле давления, и с учётом (9) сумма вкладов всех
четырёх полей обнуляется.
В (13) представлены пять различных масс
физической системы, наименьшая из которых есть 
, а наибольшая – масса 
.
Масса больше, чем инвариантная масса системы 
,
поскольку вклад в общую энергию от гравитационного поля отрицателен и в космических
системах превышает
вклады других полей. Масса есть сумма инвариантных масс частиц системы, и
эта масса равна гравитационной массе 
системы. Масса по своей величине
близка к суммарной массе барионов и электронов вещества, используемой в общей
теории относительности. Однако в нашем подходе масса 
совпадает с массой и не равна 
. Это связано с тем, что массы 
и мы вычисляли в рамках
ковариантной теории гравитации.
Мы можем считать, что массы и предназначены скорее для внешнего наблюдателя,
оценивающего гравитационные и инертные свойства системы. Масса связана с гравитационными воздействиями,
которые система оказывает на другие тела, либо с теми воздействиями, которые
оказывают внешние тела на рассматриваемую систему. Инвариантная
масса системы
входит в выражение для энергии и импульса системы и потому отражает инертные
свойства системы с точки зрения действия на неё не гравитационных сил.
Массы и могут быть важны для внутреннего наблюдателя,
который пытается определить сумму инвариантных масс частиц системы, а также
энергию взаимодействия этих частиц с полями. Масса 
позволяет путём деления на объём системы
оценить среднюю плотность 
частиц в системе их покоя.
Кроме масс, рассматриваемая система характеризуется
двумя электрическими зарядами. Один из этих зарядов определяется выражением 
и пропорционален
объёму 
системы и инвариантной плотности заряда 
,
измеренной в сопутствующих движущимся частицам системам отсчёта. Другой заряд 
согласно (8) задаёт электромагнитное поле
системы за её пределами, причём 
.
Различие данных зарядов связано с движением частиц и различием плотности заряда
у движущейся и неподвижной частицы с точки зрения теории относительности.
Список использованных источников
1.
Fedosin S.G. The Concept of the General
Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; Концепция
общего силового векторного поля.
2.
Fedosin S.G. Two components of the macroscopic general field. Reports in
Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025; Две компоненты макроскопического общего поля.
3.
Fedosin S.G.
Estimation of the physical parameters of planets and stars in the gravitational
equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров планет и звёзд в модели гравитационного
равновесия.
4. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023; Гамильтониан в ковариантной теории гравитации.
5.
Fedosin S.G. Relativistic Energy and Mass in the
Weak Field Limit. Jordan Journal of
Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210;
Релятивистская энергия и масса в пределе
слабого поля.
6. Fedosin S.G.
The virial theorem and the
kinetic energy of particles of a macroscopic system in the general field
concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue
2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и
кинетическая энергия частиц макроскопической системы в
концепции общего поля.
7.
Fedosin S.G. About the cosmological constant,
acceleration field, pressure field and energy. Jordan Journal of
Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304;
О космологической постоянной, поле ускорения,
поле давления и об энергии.
8. Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model
within the Framework of the Covariant Theory of Gravitation. International
Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
9. Fedosin S.G. The generalized
Poynting theorem for the general field and solution of the 4/3 problem.
International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19; Обобщённая
теорема Пойнтинга для
общего поля и
решение проблемы 4/3.
10.
Fedosin S.G. The Integral
Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure
Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). https://dx.doi.org/10.11648/j.ajmp.20140304.12; Интегральный 4-вектор энергии-импульса и анализ
проблемы 4/3 на основе поля давления и поля ускорений.
11.
Fedosin S.G. The electromagnetic field in the relativistic uniform
model. International Journal of Pure and Applied Sciences, Vol. 4, Issue. 2,
pp. 110-116 (2018). http://dx.doi.org/10.29132/ijpas.430614;
Электромагнитное поле в релятивистской
однородной модели.
12. Fedosin S.G. The binding energy and the total energy of a macroscopic
body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
Источник: http://sergf.ru/mh.htm