International Journal of Pure and Applied Sciences, Vol. 4, Issue. 2, pp. 110-116 (2018). http://dx.doi.org/10.29132/ijpas.430614.
Электромагнитное поле в релятивистской
однородной модели
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Для релятивистской однородно заряженной системы с инвариантной плотностью
заряда вычисляются потенциалы и напряжённости электромагнитного поля, энергии
частиц и поля. Показывается отличие релятивистского подхода от классической
однородной модели. Подтверждается вывод о том, что в отсутствие общего
магнитного поля энергия частиц, связанная со скалярным потенциалом поля, по
модулю в два раза превышает энергию, определяемую через тензорный инвариант
электромагнитного поля, входящий в гамильтониан системы.
Ключевые слова:
Релятивистская однородная система; электромагнитное поле.
The electromagnetic field in the relativistic uniform model
Sergey G. Fedosin
PO box
614088, Sviazeva
str. 22-79, Perm, Perm Krai, Russia
E-mail: fedosin@hotmail.com
The
potentials and the field strengths of the electromagnetic field, the energies
of particles and of the field are calculated for the relativistic uniformly
charged system with invariant charge density. The difference between the
relativistic approach and the classical uniform model is shown. The conclusion
is proved that in the absence of the general magnetic field the energy of
particles, associated with the scalar field potential, is twice as large in the
absolute value as the energy, determined with the help of the tensor invariant
of the electromagnetic field, which is part of the system’s Hamiltonian.
Keywords: Relativistic uniform system; electromagnetic
field.
1. Введение
В классической физике широко используется идеальная однородная модель тела,
в которой плотность массы постоянна по всему объёму тела либо задаётся как
средняя по объёму величина. Подобная модель упрощает решение физических задач и
позволяет быстро оценивать различные физические величины. Например, масса тела
вычисляется простым умножением плотности массы на объём тела, что проще, чем
интегрирование плотности по объёму в случае зависимости плотности от координат.
Недостатком классической модели является то, что большинство реальных
физических систем далеки от подобной идеальной однородности.
Применение понятия релятивистской однородной системы основано на
специальной теории относительности и является следующим шагом на пути более
точного описания физических систем. В релятивистском подходе используется
инвариантная плотность заряда (и инвариантная плотность массы) частиц,
составляющих систему. За счёт движения частиц эффективная плотность заряда и
плотность массы в системе отличаются от инвариантных значений, что вносит
дополнительные поправки в значения функций поля и в энергию системы.
Ранее свойства релятивистской однородной системы изучались в [1-3]. Целью
настоящей работы является уточнение результатов в отношении электромагнитного
поля, вычисление поправок второго порядка, а также проверка соотношения между
вкладами в релятивистскую энергию системы от энергии частиц в скалярном электрическом потенциале и от
собственной энергии электрического поля. Полученные результаты могут быть
применены для оценки свойств таких релятивистских объектов, как протон и
соответствующая ему заряженная нейтронная звезда. Указанные объекты достаточно
однородны, поскольку в них центральная эффективная плотность массы превышает
эффективную среднюю плотность всего лишь в 1,5 раза [3, 4]. Мы предполагаем,
что распределение эффективной плотности электрического заряда по объёму этих
объектов подобно распределению эффективной плотности массы, что для протона
подтверждается в [5, 6]. В таком случае мы можем считать, что возникновение радиальной
зависимости эффективной плотности связано в основном с радиальной зависимостью
скорости движения частиц, при почти неизменной инвариантной плотности массы и
заряда. Вследствие этого применение релятивистской однородной модели становится
вполне оправданным, по крайней мере в качестве первого приближения.
С другой стороны, применяемый нами теоретический
подход был бы не эффективен в отношении объектов, в которых электромагнитные
силы между зарядами были бы сравнимы по величине с гравитационными силами. В
этом случае из-за отталкивания зарядов друг от друга можно ожидать скорее
распределения заряда по поверхности, чем какого-либо однородного распределения
по объёму. Однако для нейтронных звёзд и протонов кроме гравитации имеются
дополнительные силы, скрепляющие их вещество и препятствующие переносу заряда.
В случае нейтронных звёзд это сильное взаимодействие между близко
расположенными друг к другу нуклонами, которое существенно увеличивает энергию
связи.
В следующих разделах путём решения уравнений электромагнитного
поля внутри и снаружи неподвижной релятивистской однородной системы будут
определены основные характеристики поля, включая зависимости электрического
потенциала и напряжённости поля от текущего радиуса, а также вклад в энергию
системы от энергии заряженных частиц в электрическом поле и вклад от тензорного
инварианта. Затем эти энергии будут сравнены с электростатической энергией
системы и с энергией, вычисляемой с помощью тензора энергии-импульса
электромагнитного поля.
2. Потенциалы и напряжённости поля
В качестве релятивистской однородной системы удобно
рассматривать сферическую систему, состоящую из нейтральных частиц с небольшой
добавкой заряженных частиц. Стабильность системы может поддерживаться действием
гравитации, внутренним полем давления и полем ускорений частиц [7, 8]. При этом
поле ускорений кинематически, а не динамически отслеживает движение частиц. Это
позволяет через тензор энергии-импульса поля ускорений уникальным образом
вычислять энергию и 4-ускорение частиц, в отличие от множества других вариантов
тензоров энергии-импульса вещества. В [9] было показано, что благодаря полю
ускорений в системе возникает дополнительное ускорение, противодействующее силе
гравитации и изменяющее соотношение энергий в теореме вириала. Условие
равновесия рассматриваемой системы следует из уравнения движения,
представленного в [8] в общем виде и в [9] для типичных частиц, каждая из
которых занимает репрезентативный элемент объёма и задаёт основные свойства
системы. Для потенциалов всех четырёх полей справедливы волновые уравнения,
причём при нулевой плотности вещества в решении для поля давления и поля
ускорений потенциалы этих полей обращаются в нуль. Для напряжённостей и
соленоидальных векторов полей используются уравнения, структура которых
совпадает со структурой уравнений Максвелла.
Функции поля вычисляются в предположении, что в
системе отсутствует общее вращение частиц и они в каждой точке движутся
хаотически. Это приводит к отсутствию массовых и электрических токов внутри
системы, к обнулению глобальных векторных потенциалов и соленоидальных векторов
всех полей. Действительно, из решения волновых уравнений для одиночной
движущейся заряженной частицы следует, что векторный потенциал
электромагнитного поля частицы направлен вдоль её скорости. Если взять объём
любой части системы, содержащий достаточно большое количество частиц, и
просуммировать векторные потенциалы этих частиц, то ввиду разнонаправленности
скоростей частиц глобальный векторный потенциал в каждом таком объёме будет
стремиться к нулю. То же самое можно сказать и в отношении магнитного поля,
которое вычисляется как ротор от глобального векторного потенциала. Магнитное
поле за пределами рассматриваемой системы также получается равным нулю.
Аналогично можно рассматривать и другие используемые нами поля, включая их
глобальные векторные потенциалы и соленоидальные векторы.
В принципе, вывод о том, что векторный потенциал
частицы направлен вдоль её скорости, может быть сделан и без решения уравнений
поля. Для этого достаточно учесть общее определение 4-потенциала векторного
поля для твёрдой однородной частицы [7]. С другой стороны, при решении
уравнений мы используем калибровку Лоренца, связывающую частную производную по
времени от скалярного потенциала и дивергенцию от векторного потенциала. Ввиду
стационарности поля скалярный потенциал не зависит от времени и тогда
дивергенция от векторного потенциала должна быть равна нулю, а линии векторного
потенциала должны быть замкнуты. Поскольку хаотичность движения частиц не позволяет
замкнуть эти линии, то усреднённый по некоторому объёму системы векторный
потенциал становится равным нулю.
Неоднородное электромагнитное волновое уравнение
для скалярного потенциала внутри сферы имеет стандартный вид:
.
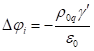(1)
В (1) фактор Лоренца типичных частиц 
, 
– среднеквадратичная
скорость движения произвольной частицы внутри сферы, 
– скорость света, 
– электрическая постоянная, 
– плотность заряда частицы в сопутствующей частице системе
отсчёта, индекс 
отличает внутренний
потенциал 
от внешнего потенциала
, который генерирует сфера за своими пределами. Величина 
в (1)
представляет собой эффективную плотность заряда. Как потенциал , так и 
являются функциями
текущего радиуса 
внутри сферы и не
зависят от угловых переменных, а также от времени ввиду стационарности всех полей.
Поэтому в сферических координатах в лапласиане достаточно взять лишь ту его
часть, которая зависит от радиуса:
.
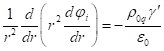Если сделать
замену переменных в виде 
, то уравнение
переписывается так:
.
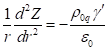Зависимость от радиуса была вычислена в
[1]:
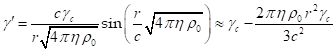, (2)
где 
– фактор Лоренца частиц в центре сферы, 
–
коэффициент поля ускорений, 
– инвариантная
плотность массы частиц.
Подставляя (2) в
уравнение для 
, имеем:
.
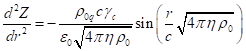Общее решение
данного уравнения имеет вид:
.
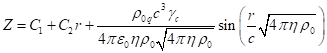Так как , и в центре при 
потенциал не может
быть бесконечным, то коэффициент 
должен быть равен
нулю. Отсюда потенциал внутри сферы будет равен:
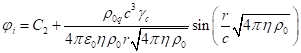. (3)
Перейдём теперь к
вычислению внешнего электрического потенциала 
неподвижной сферы,
наполненной движущимися заряженными частицами. Вначале найдём напряжённость внешнего электрического поля
сферы. Уравнения Максвелла электромагнитного поля имеют стандартный вид:
, 
, 
, 
. (4)
Согласно (4), частицы, движущиеся внутри сферы со
скоростями 
, генерируют вокруг себя электромагнитное поле с напряжённостью 
и магнитным полем 
. Окружим сферу оболочкой сферической формы с произвольным
радиусом 
и проинтегрируем
первое уравнение в (4)
по объёму оболочки. При этом применим теорему Гаусса, заменяя интеграл от
дивергенции 
на интеграл от вектора
по поверхности 
оболочки. Ввиду
симметрии сферы при постоянной плотности 
для вектора за пределами сферы
находим:
. (5)
Вектор 
в (5) обозначает
единичный вектор нормали к поверхности оболочки, направленный наружу.
Интегрирование по объёму 
оболочки сводится к
интегрированию по объёму 
сферы, так как за пределами
сферы 
. Подставляя сюда из (2) и интегрируя,
получим модуль напряжённости поля за пределами сферы и саму напряжённость поля,
направленную радиально:
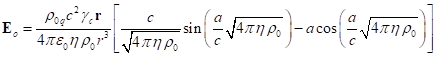. (6)
.
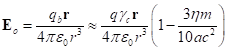Масса 
в (6) определяется как
произведение плотности массы 
на объём сферы.
Вспомогательный заряд 
равен произведению
плотности заряда на объём сферы: 
. Однако фактически электрическое поле за пределами сферы
определяется зарядом 
, согласно (5-6) равным:
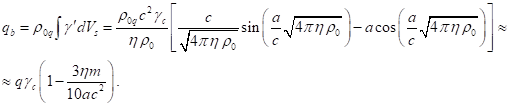
Связь между векторами электромагнитного поля и 4-потенциалом
следующая:
, 
,
(7)
где индексы 
и не совпадают друг с
другом.
Пространственные компоненты 
4-потенциала являются
компонентами векторного потенциала 
, который в данном случае равен нулю. Следовательно, в (7)
компоненты 
вектора 
связаны только с
временной компонентой 
4-потенциала: 
. Это равенство в векторных обозначениях запишется так: 
. Отсюда с учётом выражения (6) для 
следует, что:
.
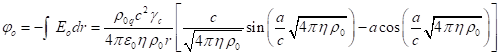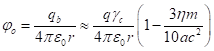. (8)
На бесконечности
этот потенциал становится равным нулю. На поверхности сферы потенциал (8) должен совпасть с внутренним потенциалом в
(3). Положим 
и приравняем оба
потенциала. Это позволяет определить коэффициент 
и уточнить внутренний
потенциал 
:
,
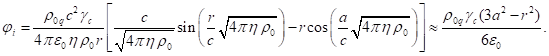
(9)
Теперь можно
вычислить напряжённость электрического поля внутри сферы. Учитывая равенство
нулю векторного потенциала 
, имеем:
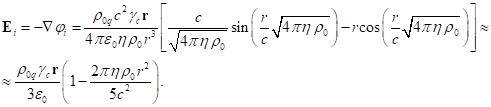
(10)
В (10) мы добавили следующий член разложения,
содержащий в знаменателе квадрат скорости света, и показывающий отличие
релятивистской однородной системы от классического случая.
3. Энергия частиц и поля
Вычислим вначале вклад в релятивистскую энергию
системы от энергии частиц в электрическом поле, который определяется в [8] как
интеграл по объёму от произведения эффективной плотности заряда внутри сферы 
на внутренний
скалярный потенциал 
. С учётом (2) и (9) имеем:
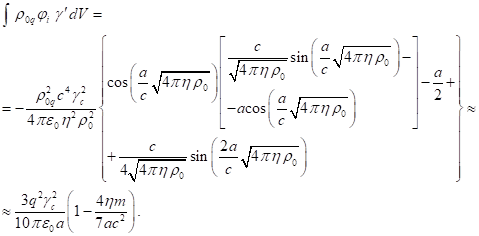(11)
Заметим, что полученное в (11) значение энергии в два раза
больше, чем электростатическая энергия заряженных частиц внутри сферы.
Вычислим теперь интеграл по объёму от тензорного
инварианта электромагнитного поля, отдельно для поля внутри и снаружи сферы.
Интеграл от тензорного инварианта выражается через напряжённость электрического
поля и магнитную индукцию:
.
В таком виде данный интеграл входит в релятивистскую
энергию системы и задаёт там вклад электромагнитного поля [8]. Подставляя сюда
(10) и (6) и учитывая, что 
, находим:
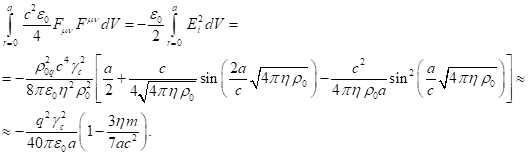
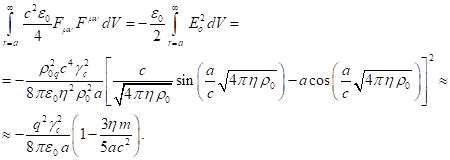
(12)
Заключение
В [10] в рамках ковариантной гравитации для
гравитационного поля был сделан вывод о том, что вклад в релятивистскую энергию
системы от энергии покоящегося вещества в гравитационном скалярном потенциале
по модулю превышает в два раза интеграл от тензорного инварианта
гравитационного поля, и это же справедливо для электромагнитного поля.
Изменится ли что-либо в случае релятивистской однородной системы, в которой
частицы вещества не стоят на месте, а движутся с лоренц-фактором (2), зависящим
от текущего радиуса?
Для ответа на этот вопрос мы можем просуммировать
интегралы в (12) от тензорного инварианта как внутри, так и снаружи сферы, и
сравнить результат с (11). Это даёт:
(13)
Таким образом, соотношение для энергий не зависит от
типа однородности системы – как в классическом, так и в релятивистском случае
соотношение остаётся прежним. Следует заметить, что вследствие хаотического
движения частиц суммарная индукция магнитного поля везде равна нулю, и потому
сумма интегралов в левой части (13) по модулю равна электрической потенциальной
энергии системы.
На первый взгляд такое совпадение может показаться
случайным. Действительно, вклад в релятивистскую энергию системы от энергии
частиц в электрическом поле из (11) в два раза превышает электрическую
потенциальную энергию и при 
с точностью до знака
равняется удвоенной величине интеграла от тензорного инварианта в левой части
(13). Однако общепринято, что энергия электромагнитного поля положительна и
вычисляется путём интегрирования по объёму временной компоненты 
тензора
энергии-импульса электромагнитного поля. Полученная таким образом энергия поля
отличается своим знаком от интеграла тензорного инварианта, который
отрицателен. Из всего этого следует, что члены в релятивистской энергии
системы, ответственные за энергию частиц в электромагнитном поле и за энергию
самого электромагнитного поля, отличаются как от электростатической энергии,
так и от энергии поля, вычисляемой с помощью тензора энергии-импульса.
Если учесть, что эффективная плотность заряда
внутри сферы есть 
, то два варианта для оценки электростатической
энергии, используемые в электростатике, можно представить так:
. (14)
Электростатическая энергия 
представляет собой
полный вклад, вносимый в релятивистскую энергию системы благодаря присутствию в
системе электрических зарядов. Так, в [11] энергия 
вычисляется методом
виртуальной работы путём переноса зарядов из бесконечности на сферу до тех пор,
пока сфера не достигнет заданного радиуса. При выполнении такой работы заряды
приобретают энергию в электрическом потенциале сферы, растёт также энергия
самого поля. Таким образом, энергия включает в себя две
компоненты – энергию зарядов в электрическом потенциале, и энергию поля.
Сложим теперь левые части равенств (11) и (13) для того, чтобы найти полный
вклад в релятивистскую
энергию системы, возникающий от присутствия
электрических зарядов. Если учесть правую часть (13) и определение
электростатической энергии (14), мы снова получим энергию . Отсюда видно, что действительно вклад в энергию системы делает
как энергия зарядов в электрическом потенциале, так и энергия поля. Однако, как
было указано выше, данные энергии не совпадают ни с электростатической
энергией, ни с энергией поля, находимой через тензор энергии-импульса
электромагнитного поля. Это происходит вследствие различия ковариантного
подхода, учитывающего принцип наименьшего действия, и нековариантного подхода
классической электростатики.
Заметим ещё, что соотношение (13) можно трактовать
как пример действия теоремы о равнораспределении энергии. Согласно этой
теореме, степени свободы, входящие квадратичным образом в гамильтониан, вносят
вклад в энергию системы в два раза меньше, чем степени свободы, входящие в
гамильтониан линейным образом [12]. Напряжённость электрического поля входит в
тензорный инвариант квадратичным способом, а потенциал электрического поля
входит в релятивистскую энергию линейным образом. В результате согласно (13)
напряжённость и потенциал поля можно считать отдельными и независимыми
степенями свободы электромагнитного поля, одинаково необходимыми для описания
процессов в поле.
Список использованных
источников
1.
Fedosin S.G. Relativistic
Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No.
1, pp. 1-16 (2015). // Релятивистская энергия и масса в пределе слабого поля.
2.
Fedosin S.G. The Integral
Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure
Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12. // Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля
давления и поля ускорений.
3.
Fedosin S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model.
Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593. // Оценка физических
параметров планет и звёзд в модели гравитационного равновесия.
4.
Fedosin S.G. The radius
of the proton in the self-consistent model. Hadronic Journal, Vol.
35, No. 4, pp.
349-363 (2012). // Радиус протона в самосогласованной
модели.
5. Kelly
J. J. Nucleon Charge and Magnetization Densities, arXiv:hep-ph/0111251.
6. Ulugbek
Yakhshiev and Hyun-Chul Kim. Transverse charge densities in the nucleon in
nuclear matter. Physics Letters B, Vol. 726, Issues 1–3, pp. 375-381 (2013). http://dx.doi.org/10.1016/j.physletb.2013.08.004.
7. Fedosin S.G. The Procedure of Finding the Stress-Energy Tensor
and Equations of Vector Field of Any Form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101. // Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
8.
Fedosin S.G. About the cosmological
constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016); О
космологической постоянной, поле ускорения, поле давления и об энергии.
9. Fedosin S.G. The virial theorem and the kinetic energy of
particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и кинетическая энергия частиц макроскопической системы в концепции общего поля.
10.
Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023. // Гамильтониан в ковариантной теории гравитации.
11. Feynman R, Leighton R, and Sands M. The Feynman Lectures on Physics. Volume 2. Addison Wesley, 1964.
12.
Huang, K. (1987). Statistical Mechanics (2nd ed.).
John Wiley and Sons. pp. 136-138.
Источник:
http://sergf.ru/elp.htm