Fedosin's theorem

Fedosin's theorem

Fedosin's theorem is a theorem on the magnetic field of rotating charged bodies in classical electrodynamics. It was proven by Sergey Fedosin in 2021. ^[1]

The theorem states that the magnetic field on the rotation axis of an axisymmetric charged body or charge distribution has only one component directed along the rotation axis, and the magnetic field is expressed through the surface integral, which does not require integration over the azimuthal angle $~\phi$ . In the general case, for arbitrary charge distribution and for any location of the rotation axis, the magnetic field is expressed through the volume integral, in which the integrand does not depend on the angle $~\phi$ .

Contents

· 1 Proof of theorem

· 2 Application

o 2.1 Cylinder

o 2.2 Ball

· 3 Significance of the theorem

· 4 References

· 5 See also

· 6 External links

Proof of theorem

The starting point in the proof of the theorem is the electromagnetic Liénard–Wiechert potential. For the vector potential of a rotating charged body, the following is obtained:

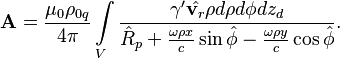
$~{\mathbf A}={\frac {\mu _{0}\rho _{{0q}}}{4\pi }}\int \limits _{V}{\frac {\gamma '{\hat {{\mathbf v}_{r}}}\rho d\rho d\phi dz_{d}}{{\hat R}_{p}+{\frac {\omega \rho x}{c}}\sin {\hat \phi }-{\frac {\omega \rho y}{c}}\cos {\hat \phi }}}.$

where $~\mu _{0}$ is the vacuum permeability; $~\rho _{{0q}}$ is the invariant charge density of the matter; $~\gamma '$ is the Lorentz factor for the velocity of chaotic motion of matter charged particles; $~{\hat {{\mathbf v}_{r}}}$ is the linear rotational velocity of an arbitrary point in the volume of the body at an early moment of time $~{\hat t}=t-{\frac {{\hat R}_{p}}{c}}$ ; $~dV=\rho d\rho d\phi dz_{d}$ is the volume element of a non-rotating body in cylindrical coordinates; $~{\hat R}_{p}$ is the distance taken at an early time from a point inside the body to a point with a radius vector $~{\mathbf R}=(x,y,z)$ , where the vector potential is sought; $~\omega$ is the constant angular velocity; is the speed of light; $~{\hat \phi }$ is the azimuth angle of an arbitrary point in the volume of the body, taken at the early time.

The magnetic field is determined by the formula $~{\mathbf B}=\nabla \times {\mathbf A}$ . When calculating the rotor, it is necessary to find the partial derivatives $~{\frac {\partial }{\partial x}}$ , $~{\frac {\partial }{\partial y}}$ and $~{\frac {\partial }{\partial z}}$ from the values $~{\hat {{\mathbf v}_{r}}}$ , $~{\hat R}_{p}$ , $~\sin {\hat \phi }$ and $~\cos {\hat \phi }$ .

If the axis of rotation of the body is directed along the axis, the magnetic field on this axis has only one component equal to

$~B_{z}(OZ)={\frac {\mu _{0}\omega \rho _{{0q}}}{4\pi }}\int \limits _{V}{\frac {\gamma '\rho ^{3}d\rho d\phi dz_{d}}{\left[(z-z_{d})^{2}+\rho ^{2}\right]^{{3/2}}}}.$

From this it can be seen that the integrand does not depend on the azimuthal angle $~\phi$ for any position of the axis of rotation. For axisymmetric bodies, the formula for the magnetic field on the axis of rotation is simplified and ceases to depend on the angle $~\phi$ :

$~B_{z}(OZ)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\int \limits _{V}{\frac {\gamma '\rho ^{3}d\rho dz_{d}}{\left[(z-z_{d})^{2}+\rho ^{2}\right]^{{3/2}}}}.\qquad (1)$

Application

Cylinder

Formula (1) as applied to a uniformly charged rotating cylinder of length and radius , without taking into account the chaotic motion of charged particles ( $~\gamma '=1$ ), when the origin of the coordinate system is at the center of the cylinder, gives the following for the field on the axis of rotation outside the cylinder:

$~B_{z}(z\geq L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left(z+{\frac {L}{2}}\right){\sqrt {\left(z+{\frac {L}{2}}\right)^{2}+a^{2}}}-\left(z-{\frac {L}{2}}\right){\sqrt {\left(z-{\frac {L}{2}}\right)^{2}+a^{2}}}+\left(z-{\frac {L}{2}}\right)^{2}-\left(z+{\frac {L}{2}}\right)^{2}\right].$

At the end face of the cylinder at it turns out

$~B_{z}(z=L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left(L{\sqrt {L^{2}+a^{2}}}-L^{2}\right)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{4}}.$

The magnetic field inside the cylinder on the axis of rotation is:

$~B_{z}(0\leq z\leq L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left({\frac {L}{2}}+z\right){\sqrt {\left({\frac {L}{2}}+z\right)^{2}+a^{2}}}-\left({\frac {L}{2}}+z\right)^{2}\right]+{\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left({\frac {L}{2}}-z\right){\sqrt {\left({\frac {L}{2}}-z\right)^{2}+a^{2}}}-\left({\frac {L}{2}}-z\right)^{2}\right].$

At the center of the cylinder for the magnetic field, we obtain

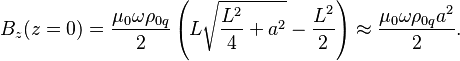
$~B_{z}(z=0)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left(L{\sqrt {{\frac {L^{2}}{4}}+a^{2}}}-{\frac {L^{2}}{2}}\right)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{2}}.$

For a long cylinder with , the magnetic field in the center is almost twice as large as that at the end of the cylinder on the axis of rotation.

For large , an approximate formula is valid:

$~B_{z}(z>>L/2)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{4}L}{8z^{3}}}.$

Ball

Formula (1) for the magnetic field on the rotation axis can be written in spherical coordinates:

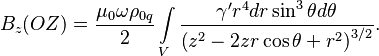
$~B_{z}(OZ)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\int \limits _{V}{\frac {\gamma 'r^{4}dr\sin ^{3}\theta d\theta }{\left(z^{2}-2zr\cos \theta +r^{2}\right)^{{3/2}}}}.$

For a solid ball of radius , in which the proper chaotic motion of charges is not taken into account, $~\gamma '=1$ . If the origin of the coordinate system is in the center of the ball, the formulas will be valid for the external field on the axis of rotation and at the pole of the ball:

$~B_{z}(z\geq a)={\frac {2\mu _{0}\omega \rho _{{0q}}a^{5}}{15z^{3}}}.$

$~B_{z}(z=a)={\frac {2\mu _{0}\omega \rho _{{0q}}a^{2}}{15}}.$

When in the center of the ball, the field is

$~B_{z}(z=0)={\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{3}}.$

Significance of the theorem

The formulas found in the proof of the theorem make it possible to determine the external magnetic field of rotating charged bodies, as well as the field at their center. In addition, the results obtained make it possible to calibrate the complete solutions for the magnetic field of rotating bodies that satisfy the wave equations.

References

1. Fedosin S.G. The Theorem on the Magnetic Field of Rotating Charged Bodies. Progress In Electromagnetics Research M, Vol. 103, pp. 115-127 (2021). http://dx.doi.org/10.2528/PIERM21041203 . ArXiv 2107.07418. Bibcode 2021arXiv210707418F.

See also

§ Field energy theorem

§ Equation of vector field

§ Electromagnetic field

§ Electromagnetic field of cylinder

External links

Source: http://sergf.ru/ften.htm

On the list of pages