Теорема Федосина

Теорема Федосина

Теорема Федосина представляет собой теорему о магнитном поле вращающихся заряженных тел в классической электродинамике. Была доказана Сергеем Федосиным в 2021 году. ^[1].

Содержание

1 Формулировка
2 Доказательство
3 Проверка

o 3.1 Цилиндр

o 3.2 Шар

4 Значение теоремы
5 Ссылки
6 См. также
7 Внешние ссылки

Формулировка

Теорема утверждает, что магнитное поле на оси вращения осесимметричного заряженного тела или распределения зарядов имеет только одну компоненту, направленную вдоль оси вращения, причём магнитное поле выражается через интеграл по поверхности, не требующий интегрирования по азимутальному углу $~\phi$ . В общем случае для произвольного распределения зарядов и при любом расположении оси вращения магнитное поле выражается через интеграл по объёму, в котором подынтегральное выражение не зависит от $~\phi$ .

Доказательство

Исходной точкой при доказательстве теоремы являются электромагнитные потенциалы Лиенара — Вихерта. Для векторного потенциала вращающегося заряженного тела получается следующее:

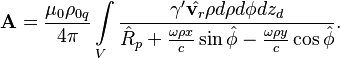
$~{\mathbf A}={\frac {\mu _{0}\rho _{{0q}}}{4\pi }}\int \limits _{V}{\frac {\gamma '{\hat {{\mathbf v}_{r}}}\rho d\rho d\phi dz_{d}}{{\hat R}_{p}+{\frac {\omega \rho x}{c}}\sin {\hat \phi }-{\frac {\omega \rho y}{c}}\cos {\hat \phi }}}.$

где $~\mu _{0}$ – магнитная постоянная; $~\rho _{{0q}}$ – инвариантная плотность заряда вещества тела; $~\gamma '$ – фактор Лоренца для хаотической скорости движения заряженных частиц в системе отсчёта, вращающейся вместе с телом; $~{\hat {{\mathbf v}_{r}}}$ – линейная скорость вращения произвольной точки в объёме тела в ранний момент времени $~{\hat t}=t-{\frac {{\hat R}_{p}}{c}}$ ; $~dV=\rho d\rho d\phi dz_{d}$ есть элемент объёма не вращающегося тела в цилиндрических координатах; $~{\hat R}_{p}$ – взятое в раннее время расстояние от точки внутри тела до точки с радиус-вектором $~{\mathbf R}=(x,y,z)$ , где ищется векторный потенциал; $~\omega$ – угловая скорость вращения тела; – скорость света; $~{\hat \phi }$ – азимутальный угол произвольной точки в объёме тела, взятый в раннее время.

Магнитное поле определяется по формуле $~{\mathbf B}=\nabla \times {\mathbf A}$ . При вычислении ротора необходимо находить частные производные $~{\frac {\partial }{\partial x}}$ , $~{\frac {\partial }{\partial y}}$ и $~{\frac {\partial }{\partial z}}$ от величин $~{\hat {{\mathbf v}_{r}}}$ , $~{\hat R}_{p}$ , $~\sin {\hat \phi }$ и $~\cos {\hat \phi }$ .

Если ось вращения тела направлена вдоль оси , магнитное поле на этой оси имеет только одну компоненту, равную

$~B_{z}(OZ)={\frac {\mu _{0}\omega \rho _{{0q}}}{4\pi }}\int \limits _{V}{\frac {\gamma '\rho ^{3}d\rho d\phi dz_{d}}{\left[(z-z_{d})^{2}+\rho ^{2}\right]^{{3/2}}}}.$

Отсюда видно, что подынтегральное выражение не зависит от азимутального угла $~\phi$ при любом расположении оси вращения. Для осесимметричных тел формула для магнитного поля на оси вращения упрощается и перестаёт зависеть от угла $~\phi$ :

$~B_{z}(OZ)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\int \limits _{V}{\frac {\gamma '\rho ^{3}d\rho dz_{d}}{\left[(z-z_{d})^{2}+\rho ^{2}\right]^{{3/2}}}}.\qquad (1)$

Проверка

Цилиндр

Формула (1) в применении к однородно заряженному вращающемуся цилиндру длиной и радиусом , без учёта хаотического движения заряженных частиц ( $~\gamma '=1$ ), при расположении начала системы координат в центре цилиндра даёт следующее для поля на оси вращения за пределами цилиндра:

$~B_{z}(z\geq L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left(z+{\frac {L}{2}}\right){\sqrt {\left(z+{\frac {L}{2}}\right)^{2}+a^{2}}}-\left(z-{\frac {L}{2}}\right){\sqrt {\left(z-{\frac {L}{2}}\right)^{2}+a^{2}}}+\left(z-{\frac {L}{2}}\right)^{2}-\left(z+{\frac {L}{2}}\right)^{2}\right].$

На торце цилиндра при получается

$~B_{z}(z=L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left(L{\sqrt {L^{2}+a^{2}}}-L^{2}\right)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{4}}.$

Магнитное поле внутри цилиндра равно:

$~B_{z}(0\leq z\leq L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left({\frac {L}{2}}+z\right){\sqrt {\left({\frac {L}{2}}+z\right)^{2}+a^{2}}}-\left({\frac {L}{2}}+z\right)^{2}\right]+{\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left({\frac {L}{2}}-z\right){\sqrt {\left({\frac {L}{2}}-z\right)^{2}+a^{2}}}-\left({\frac {L}{2}}-z\right)^{2}\right].$

В центре цилиндра для магнитного поля получается

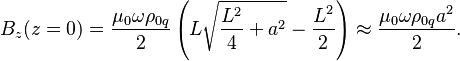
$~B_{z}(z=0)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left(L{\sqrt {{\frac {L^{2}}{4}}+a^{2}}}-{\frac {L^{2}}{2}}\right)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{2}}.$

У длинного цилиндра, у которого , магнитное поле в центре почти в два раза больше, чем на торце цилиндра на оси вращения.

При больших справедлива приблизительная формула:

$~B_{z}(z>>L/2)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{4}L}{8z^{3}}}.$

Шар

Формула (1) для магнитного поля на оси вращения может быть записана в сферических координатах:

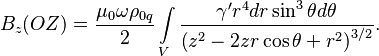
$~B_{z}(OZ)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\int \limits _{V}{\frac {\gamma 'r^{4}dr\sin ^{3}\theta d\theta }{\left(z^{2}-2zr\cos \theta +r^{2}\right)^{{3/2}}}}.$

Для твёрдого шара радиуса , в котором не учитывается собственное хаотическое движение зарядов, $~\gamma '=1$ . Если начало системы координат находится в центре шара, для внешнего поля на оси вращения и на полюсе шара будут справедливы формулы:

$~B_{z}(z\geq a)={\frac {2\mu _{0}\omega \rho _{{0q}}a^{5}}{15z^{3}}}.$

$~B_{z}(z=a)={\frac {2\mu _{0}\omega \rho _{{0q}}a^{2}}{15}}.$

При в центре шара поле равно

$~B_{z}(z=0)={\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{3}}.$

Значение теоремы

Найденные при доказательстве теоремы формулы позволяют определять внешнее магнитное поле вращающихся заряженных тел, а также поле в их центре. Кроме этого, полученные результаты дают возможность осуществить калибровку полных решений для магнитного поля вращающихся тел, удовлетворяющих волновым уравнениям.

Ссылки

1. Fedosin S.G. The Theorem on the Magnetic Field of Rotating Charged Bodies. Progress In Electromagnetics Research M, Vol. 103, pp. 115-127 (2021). http://dx.doi.org/10.2528/PIERM21041203 . ArXiv 2107.07418. Bibcode 2021arXiv210707418F. // Теорема о магнитном поле вращающихся заряженных тел.

См. также

§ Теорема энергии поля

§ Уравнение векторного поля

§ Электромагнитное поле

§ Электромагнитное поле цилиндра

Внешние ссылки

§ Fedosin's theorem

Источник: http://sergf.ru/ft.htm

На список страниц