Электромагнитное поле цилиндра

Электромагнитное поле цилиндра

В электродинамике, электромагнитное поле цилиндра рассматривается как поле одного из самых простых геометрических тел. Решения для компонент электромагнитного поля для случаев неподвижного и вращающегося цилиндра ненамного сложнее, чем соответствующие решения для шара.

При вращении однородно заряженного цилиндра с постоянной угловой скоростью поле стационарно и не зависит от времени. В этом случае для электрического скалярного потенциала $~\varphi$ и для векторного потенциала $~{\mathbf A}$ из уравнений Максвелла следуют уравнения:

$~\Delta \varphi =-{\frac {\gamma \rho _{{0q}}}{\varepsilon _{0}}},\qquad (1)$

$~\Delta {\mathbf A}=-{\frac {\gamma \rho _{{0q}}}{\varepsilon _{0}c^{2}}}{\mathbf v},\qquad (2)$

где $~\Delta$ есть оператор Лапласа; $~\gamma$ – фактор Лоренца; $~\rho _{{0q}}$ – инвариантная плотность заряда вещества цилиндра; $~\varepsilon _{0}$ – электрическая постоянная; – скорость света; $~{\mathbf v}$ – линейная скорость вращения произвольной точки, взятой в объёме цилиндра.

Содержание

· 1 Длинный неподвижный цилиндр

· 2 Длинный вращающийся цилиндр

o 2.1 Векторный потенциал и магнитное поле

· 3 Ссылки

· 4 См. также

· 5 Внешние ссылки

Длинный неподвижный цилиндр

В неподвижном цилиндре фактор Лоренца заряженных частиц вещества равен $~\gamma =1$ , если не учитывать собственное хаотическое движение этих частиц. Лапласиан в (1) удобно выразить в цилиндрических координатах $~\rho \ ,\phi \ ,z$ . В достаточно длинном цилиндре можно пренебречь краевыми эффектами, существенными вблизи торцов цилиндра, и считать, что поле в основном зависит лишь от координаты $~\rho$ . В таком приближении внутри цилиндра электрический потенциал и напряжённость электрического поля равны: ^[1]

$~\varphi _{i}=-{\frac {\rho _{{0q}}\rho ^{2}}{4\varepsilon _{0}}}+{\frac {\rho _{{0q}}}{2\varepsilon _{0}}}\left[{\frac {L{\sqrt {L^{2}+4a^{2}}}}{4}}+a^{2}\operatorname {Arsh}{{\frac {L}{2a}}}-{\frac {L^{2}}{4}}\right],$

$~{\mathbf E}_{i}={\frac {\rho _{{0q}}\rho }{2\varepsilon _{0}}}{\mathbf e}_{\rho },$

где есть длина цилиндра, – радиус цилиндра, $~{\mathbf e}_{\rho }$ – единичный вектор, направленный вдоль цилиндрической координаты $~\rho$ .

Как видно, потенциал внутри цилиндра зависит от его длины логарифмически, вследствие присутствия ареасинуса $~\operatorname {Arsh}{{\frac {L}{2a}}}$ . Внутреннее электрическое поле $~{\mathbf E}_{i}$ вдалеке от торцов цилиндра при направлено перпендикулярно оси вращения и равно нулю на оси вращения, где $~\rho =0$ .

Соответствующий внешний электрический потенциал и напряжённость электрического поля за пределами длинного цилиндра имеют следующий вид:

$~\varphi _{o}=-{\frac {\rho _{{0q}}a^{2}}{2\varepsilon _{0}}}\ln {\frac {\rho }{a}}-{\frac {\rho _{{0q}}a^{2}}{4\varepsilon _{0}}}+{\frac {\rho _{{0q}}}{2\varepsilon _{0}}}\left[{\frac {L{\sqrt {L^{2}+4a^{2}}}}{4}}+a^{2}\operatorname {Arsh}{{\frac {L}{2a}}}-{\frac {L^{2}}{4}}\right],$

$~{\mathbf E}_{o}={\frac {\rho _{{0q}}a^{2}}{2\varepsilon _{0}\rho }}{\mathbf e}_{\rho }.$

Указанные выше формулы требуют коррекции вблизи торцов цилиндра, так как здесь электрический потенциал и напряжённость поля становятся функциями не только от $~\rho$ , но и от .

Длинный вращающийся цилиндр

При вращении цилиндра с постоянной угловой скоростью $~\omega$ фактор Лоренца заряженных частиц вещества становится функцией $~\rho$ :

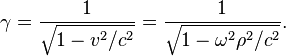
$~\gamma ={\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}={\frac {1}{{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}}}.$

С учётом этого решением уравнения (1) для скалярного потенциала, а также для напряжённости поля внутри вращающегося однородно заряженного цилиндра вдалеке от торцов цилиндра будет следующее: ^[1]

$~\varphi _{i}={\frac {c^{2}\rho _{{0q}}}{\varepsilon _{0}\omega ^{2}}}\left[{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}-\ln \left(1+{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}\right)-1+\ln 2\right]+{\frac {\rho _{{0q}}}{2\varepsilon _{0}}}\left[{\frac {L{\sqrt {L^{2}+4a^{2}}}}{4}}+a^{2}\operatorname {Arsh}{{\frac {L}{2a}}}-{\frac {L^{2}}{4}}\right],$

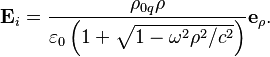
$~{\mathbf E}_{i}={\frac {\rho _{{0q}}\rho }{\varepsilon _{0}\left(1+{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}\right)}}{\mathbf e}_{\rho }.$

За пределами длинного вращающегося цилиндра скалярный потенциал и напряжённость электрического поля выражаются формулами:

$~\varphi _{o}=-{\frac {\rho _{{0q}}a^{2}}{2\varepsilon _{0}}}\ln {\frac {\rho }{a}}+{\frac {c^{2}\rho _{{0q}}}{\varepsilon _{0}\omega ^{2}}}\left[{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}-\ln \left(1+{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}\right)-1+\ln 2\right]+{\frac {\rho _{{0q}}}{2\varepsilon _{0}}}\left[{\frac {L{\sqrt {L^{2}+4a^{2}}}}{4}}+a^{2}\operatorname {Arsh}{{\frac {L}{2a}}}-{\frac {L^{2}}{4}}\right],$

$~{\mathbf E}_{o}={\frac {\rho _{{0q}}a^{2}}{2\varepsilon _{0}\rho }}{\mathbf e}_{\rho }.$

Векторный потенциал и магнитное поле

Вращение заряженного вещества цилиндра приводит к возникновению векторного потенциала $~{\mathbf A}$ и индукции магнитного поля $~{\mathbf B}$ . Для этих величин внутри цилиндра вдалеке от торцов цилиндра как следствие (2) получается следующее:

$~{\mathbf A}_{i}={\frac {\rho _{{0q}}}{\varepsilon _{0}}}\left[{\frac {c^{2}}{3\omega ^{3}\rho }}-{\frac {c^{2}}{3\omega ^{3}\rho }}\left(1-\omega ^{2}\rho ^{2}/c^{2}\right)^{{3/2}}-{\frac {\rho }{2\omega }}+{\frac {\omega \rho }{4c^{2}}}\left(L{\sqrt {{\frac {L^{2}}{4}}+a^{2}}}-{\frac {L^{2}}{2}}\right)\right]{\mathbf e}_{\phi },$

$~{\mathbf B}_{i}={\frac {\rho _{{0q}}}{\varepsilon _{0}}}\left[{\frac {1}{\omega }}{\sqrt {1-\omega ^{2}\rho ^{2}/c^{2}}}-{\frac {1}{\omega }}+{\frac {\omega }{2c^{2}}}\left(L{\sqrt {{\frac {L^{2}}{4}}+a^{2}}}-{\frac {L^{2}}{2}}\right)\right]{\mathbf e}_{z},$

где $~{\mathbf e}_{\phi }$ – единичный вектор, направленный вдоль цилиндрической координаты $~\phi$ , $~{\mathbf e}_{z}$ – единичный вектор, направленный вдоль цилиндрической координаты . Как видно, внутренний векторный потенциал вращается вокруг оси вращения цилиндра. Что касается магнитного поля, то оно направлено вдоль оси вращения, вдоль которой отсчитывается координата . При этом магнитное поле максимально на самой оси и стремится к нулю вблизи поверхности цилиндра.

Внешний векторный потенциал и магнитное поле длинного цилиндра определяются формулами:

$~{\mathbf A}_{o}={\frac {\rho _{{0q}}}{\varepsilon _{0}\rho }}\left[{\frac {c^{2}}{3\omega ^{3}}}-{\frac {c^{2}}{3\omega ^{3}}}\left(1-\omega ^{2}a^{2}/c^{2}\right)^{{3/2}}-{\frac {a^{2}}{2\omega }}+{\frac {\omega a^{2}}{4c^{2}}}\left(L{\sqrt {{\frac {L^{2}}{4}}+a^{2}}}-{\frac {L^{2}}{2}}\right)\right]{\mathbf e}_{\phi },$

$~{\mathbf B}_{o}=\nabla \times {\mathbf A}_{o}\approx 0.$

Данные формулы являются достаточно точными недалеко от центра длинного цилиндра. Однако по мере приближения к торцам цилиндра следует учесть то, что в формулах для векторного потенциала и магнитного поля появляются существенные добавки вследствие зависимости от координаты . Для бесконечно длинного цилиндра вышеприведённые формулы можно использовать без ограничений.

Теорема Федосина позволяет точно вычислять магнитное поле на оси вращения заряженных вращающихся тел. В частности, магнитное поле внутри цилиндра зависит от : ^[2]

$~B_{z}(0\leq z\leq L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left({\frac {L}{2}}+z\right){\sqrt {\left({\frac {L}{2}}+z\right)^{2}+a^{2}}}-\left({\frac {L}{2}}+z\right)^{2}\right]+{\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left({\frac {L}{2}}-z\right){\sqrt {\left({\frac {L}{2}}-z\right)^{2}+a^{2}}}-\left({\frac {L}{2}}-z\right)^{2}\right].$

В центре цилиндра при магнитное поле равно:

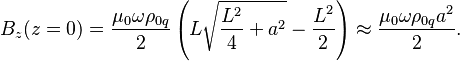
$~B_{z}(z=0)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left(L{\sqrt {{\frac {L^{2}}{4}}+a^{2}}}-{\frac {L^{2}}{2}}\right)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{2}}.$

Если брать точки на оси вращения за пределами цилиндра, то там магнитное поле имеет вид:

$~B_{z}(z\geq L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left[\left(z+{\frac {L}{2}}\right){\sqrt {\left(z+{\frac {L}{2}}\right)^{2}+a^{2}}}-\left(z-{\frac {L}{2}}\right){\sqrt {\left(z-{\frac {L}{2}}\right)^{2}+a^{2}}}+\left(z-{\frac {L}{2}}\right)^{2}-\left(z+{\frac {L}{2}}\right)^{2}\right]\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{4}L}{8z^{3}}}.$

На торце цилиндра при получается

$~B_{z}(z=L/2)={\frac {\mu _{0}\omega \rho _{{0q}}}{2}}\left(L{\sqrt {L^{2}+a^{2}}}-L^{2}\right)\approx {\frac {\mu _{0}\omega \rho _{{0q}}a^{2}}{4}}.$

В результате магнитное поле в центре почти в два раза больше, чем на торце цилиндра на оси вращения. Такое различие показывает степень влияния краевых эффектов и необходимость учёта в (2) зависимости векторного потенциала от координаты вблизи торцов цилиндра.

Ссылки

1. ^{a b} Sergey G. Fedosin. The Electromagnetic Field of a Rotating Relativistic Uniform System. Chapter 2 in the book: Horizons in World Physics. Volume 306. Edited by Albert Reimer, New York, Nova Science Publishers Inc, pp. 53-128 (2021), ISBN: 978-1-68507-077-9, 978-1-68507-088-5 (e-book). https://doi.org/10.52305/RSRF2992 // Электромагнитное поле вращающейся релятивистской однородной системы.

2. Fedosin S.G. The Theorem on the Magnetic Field of Rotating Charged Bodies. Progress In Electromagnetics Research M, Vol. 103, pp. 115-127 (2021). http://dx.doi.org/10.2528/PIERM21041203. ArXiv 2107.07418. Bibcode 2021arXiv210707418F. // Теорема о магнитном поле вращающихся заряженных тел.

См. также

· Теорема энергии поля

· Теорема Федосина

· Уравнение векторного поля

· Электромагнитное поле

Внешние ссылки

· Electromagnetic field of cylinder

Источник: http://sergf.ru/efc.htm

На список страниц