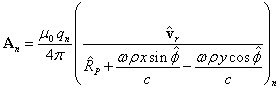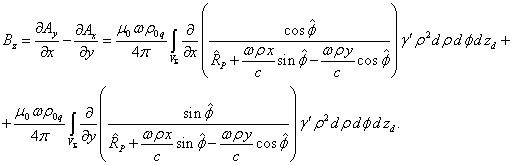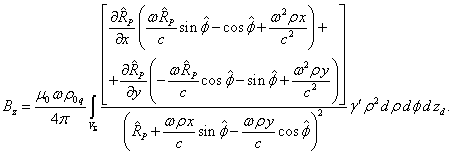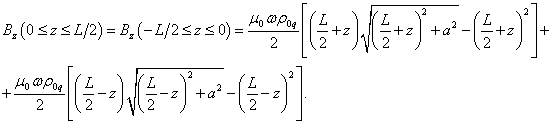Теорема о магнитном поле вращающихся заряженных тел

Progress In Electromagnetics Research M, Vol. 103, pp. 115-127 (2021). http://dx.doi.org/10.2528/PIERM21041203

Теорема о магнитном поле вращающихся заряженных тел

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

С помощью метода запаздывающих потенциалов выводится закон Био–Савара–Лапласа с учётом поправки, описывающей хаотическое движение заряженных частиц в прямолинейно направленных токах. Затем этот метод используется для круговых токов и доказывается следующая теорема: Магнитное поле на оси вращения осесимметричного заряженного тела или распределения зарядов имеет только одну компоненту, направленную вдоль оси вращения, причём магнитное поле выражается через интеграл по поверхности, не требующий интегрирования по азимутальному углу . В общем случае для произвольного распределения зарядов и при любом расположении оси вращения магнитное поле выражается через интеграл по объёму, в котором подынтегральное выражение не зависит от . Полученные простые формулы в цилиндрических и сферических координатах позволяют быстро находить внешнее и центральное магнитное поле вращающихся тел на оси вращения.

Ключевые слова: магнитное поле; закон Био–Савара–Лапласа; векторный потенциал.

The theorem on the magnetic field of rotating charged bodies

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

E-mail: fedosin@hotmail.com

The method of retarded potentials is used to derive the Biot-Savart law, taking into account the correction that describes the chaotic motion of charged particles in rectilinear currents. Then this method is used for circular currents and the following theorem is proved: The magnetic field on the rotation axis of an axisymmetric charged body or charge distribution has only one component directed along the rotation axis, and the magnetic field is expressed through the surface integral, which does not require integration over the azimuthal angle . In the general case, for arbitrary charge distribution and for any location of the rotation axis, the magnetic field is expressed through the volume integral, in which the integrand does not depend on the angle . The obtained simple formulas in cylindrical and spherical coordinates allow us to quickly find the external and central magnetic field of rotating bodies on the rotation axis.

Keywords: magnetic field; Biot-Savart law; vector potential.

1. Введение

В общем случае стационарное движение заряженной частицы складывается из прямолинейного движения с постоянной скоростью, и вращательного движения с постоянной угловой скоростью. Каждое из этих движений своим собственным способом приводит к возникновению соответствующего вектора магнитного поля, так что полное магнитное поле частицы может быть найдено путём сложения двух таких векторов магнитного поля. Если рассматривается стационарное движение множества частиц или движение заряженного тела, то полное магнитное поле системы может быть найдено на основе принципа суперпозиции как сумма векторов магнитного поля отдельных частиц.

Результат движения прямолинейного тока заряженных частиц исследован достаточно хорошо, и для этого случая существует экспериментально выведенный закон Био–Савара–Лапласа (Biot–Savart law), который в упрощенном виде можно записать так [1]:

, (1)

где есть индукция магнитного поля в некоторой фиксированной точке 1, вычисляемая с помощью интеграла по объёму области 2, занимаемой протекающими в ней токами; – магнитная постоянная; – вектор плотности электрического тока внутри области 2, зависящий от координат, но не от времени; – вектор от точки с током внутри области 2 до точки 1; величина есть векторное произведение и .

Возможны различные подходы, в которых находится формула (1). Как было показано в [2] в рамках специальной теории относительности, магнитное поле, соответствующее (1), может быть вычислено как следствие преобразований Лоренца для электромагнитной силы, действующей со стороны одной заряженной частицы на другую частицу. С тем же успехом можно использовать лоренцевское преобразование компонент электромагнитного тензора из движущейся системы отсчёта , где есть только электрическое поле , в неподвижную систему отсчёта .

Действительно, по определению , где 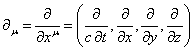есть 4-градиент, есть 4-потенциал, выражаемый через скалярный электрический потенциал , скорость света и векторный потенциал . Учитывая, что является 4-вектором, и это же справедливо для в специальной теории относительности, преобразования Лоренца могут быть применены как для , так для . При этом компоненты любого 4-вектора преобразуются точно так же, как компоненты четырёхмерной величины , задающей местоположение точки в пространстве и времени. Всё это приводит к преобразованиям Лоренца для компонент электромагнитного тензора, так что в координатной записи имеем

где четырёхмерные величины задают соответствующее преобразование Лоренца.

Поскольку ненулевые компоненты тензора равны , , , , , , то для компонент электромагнитного поля в получается следующее:

, , .

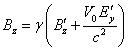, , . (2)

В выражениях (2) положим , тогда магнитное поле в будет равно 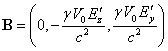, где есть скорость движения системы отсчёта в вдоль оси , фактор Лоренца . Предположим, что электрическое поле в возникает от статического распределения зарядов с постоянной плотностью зарядов . Это можно записать в виде

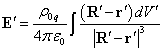где есть вектор от центра распределения до точки наблюдения, есть вектор от центра распределения до произвольной точки в объёме зарядового распределения, и интегрирование осуществляется по неподвижному в объёму распределения зарядов. Тогда магнитное поле в с учётом соотношений , можно представить формулой

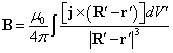где штрихованные величины задаются в .

Предположим теперь. что некоторый объём непрерывно заполнен множеством движущихся зарядовых распределений, так что , , и нам нужно найти суммарное магнитное поле за пределами объёма . В этом случае можно использовать принцип суперпозиции магнитных полей. Вместо теперь следует использовать , где есть вектор от центра объёма до точки наблюдения 1, есть вектор от центра объёма до точки 2 с плотностью тока в объёме . Это даёт

что совпадает с (1). Выражение (1) получается и из общего решения волнового уравнения для векторного потенциала в случае постоянных токов [3].

Формула (1) является одной из основных в магнитостатике для вычисления в первом приближении магнитного поля постоянных распределённых токов. Что касается случая вращательного движения заряженных частиц, то здесь ситуация более сложная, так как вращение не описывается инерциальной системой отсчёта. При вращении заряженного тела вращаются и заряженные частицы этого тела, приводя к плотности тока , причём вектор направлен обычно по касательной к кривым, по которым вращаются заряды. Не прямолинейность вектора внутри вращающегося заряженного тела заметно влияет на итоговое магнитное поле и потому вместо (1) требуется иная формула.

В [4-5] было показано, что стационарное магнитное поле осесимметричного вращающегося зарядового распределения в принципе может быть выражено через напряжённость и скалярный потенциал электрического поля этого распределения. Если же движение заряженных частиц прямолинейное, магнитное поле выражается только через , в полном соответствии с преобразованиями Лоренца для компонент тензора электромагнитного поля в инерциальных системах отсчёта. Это ещё раз подчёркивает различие прямолинейного и вращательного движений и необходимость разных формул для магнитного поля в зависимости от типа движения.

В связи с этим нашей целью будет вывод релятивистских формул для магнитных полей, возникающих от системы постоянных токов и от стационарно вращающегося зарядового распределения. В отличие от указанных выше подходов, магнитное поле будет вычисляться с учётом собственного хаотического движения зарядов. В следующем разделе мы вкратце представим релятивистское выражение для закона Био–Савара–Лапласа и оценим его точность, а в разделе 3 перейдём к анализу вращательного движения зарядов и токов и к доказательству теоремы о магнитном поле для этого случая.

2. Прямолинейное движение зарядов

Для того, чтобы оценить точность формулы (1) для магнитного поля постоянных токов, необходимо исходить из основы электромагнитной теории. В качестве отправной точки используем метод запаздывающих потенциалов [6-7], согласно которому скалярный и векторный потенциалы за пределами произвольно движущейся заряженной точечной частицы с номером выражаются формулами:

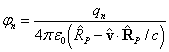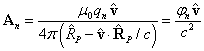, , (3)

где – заряд частицы; – электрическая постоянная; – скорость частицы в ранний момент времени ; – вектор от заряженной частицы до точки , в которой вычисляются потенциалы и ; вектор имеет длину и вычисляется в ранний момент времени ; – скорость света.

Раннее время определяется формулой:

. (4)

Смысл данного равенства заключается в том, что за время электромагнитное воздействие от заряда должно пройти путь со скоростью до точки с радиус-вектором для того, чтобы в этой точке возникли потенциалы и .

В четырёхмерном формализме пространства-времени Минковского характеристикой электромагнитного поля является 4-потенциал, который для рассматриваемой частицы имеет вид:

. (5)

Все не штрихованные величины в (5), включая , , и , измеряются в момент времени в системе отсчёта , в которой движется частица. Индекс пробегает значения , так что компонента 4-потенциала, имеющая индекс , связана со скалярным потенциалом: .

В декартовых координатах , поэтому согласно (5) компоненты 4-потенциала , , . Величина есть скалярный потенциал частицы в системе отсчёта , связанной с самой частицей; есть 4-скорость частицы. Из (5) следует, что , где есть фактор Лоренца частицы, кроме этого, , в соответствии с (3) при . Равенство означает, что специальная теория относительности в четырёхмерном формализме точна для точечных частиц либо для инерциальных систем отсчёта и в отсутствие ускорения частиц, либо с оговоркой, что следует использовать величины в запаздывающее время. Если эти условия не выполняются, то лучше вернуться к исходным принципам теории в виде (3). Для сравнения, в [3] приходят к формулам для запаздывающих потенциалов, исходя из решений волновых уравнений для потенциалов с использованием калибровки Лоренца. Тем самым показывается, что уравнения Максвелла и запаздывающие потенциалы согласуются друг с другом.

Выразим координаты точки в через координаты этой точки в с помощью преобразований Пуанкаре, учитывая, что в точка определяется радиус-вектором :

. (6)

Здесь предполагается, что при начала систем координат в и совпадали, а часы в показывали время .

Когда заряд находится в начале координат в , потенциал в точке выражается через и координаты в стандартным образом:

Подставим сюда (6) и выразим через координаты . Для этого достаточно найти квадрат длины вектора через векторы и :

. (7)

Это позволяет выразить скалярный потенциал в и векторный потенциал в :

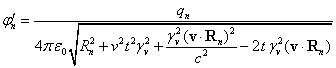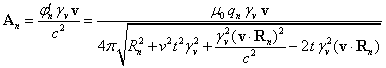Под знаком корня присутствует время , что приводит к зависимости скалярного и векторного потенциалов от времени. Это является следствием преобразования координат (6) и может рассматриваться как результат конечной скорости распространения электромагнитного воздействия и необходимости учёта его запаздывания в потенциалах Лиенара-Вихерта (3). Как правило, векторный потенциал и магнитное поле движущегося заряда ищутся в момент времени , что позволяет упростить выражение для . В большинстве случаев величина скорости намного меньше, чем скорость света, что позволяет пренебречь членом по сравнению с . С учётом этого имеем:

Расстояние с точки зрения наблюдателя в есть расстояние от заряда до точки , где ищется векторный потенциал .

Пусть теперь имеется множество близко расположенных частиц, образующих компактное пространственное распределение, движущееся как целое со скоростью . Суммарный векторный потенциал от множества заряженных частиц получается интегрированием по объёму зарядового распределения, для чего используется соотношение , где есть плотность движущегося заряда, обозначает дифференциал движущегося объёма, соответствующего объёму одной частицы. Рассмотрим ещё систему отсчёта , связанную с центром данного зарядового распределения. Если обозначить вектор от центра зарядового распределения до точки через , а вектор от центра зарядового распределения до заряда через , то будет , . С учётом всего этого для векторного потенциала распределения находим:

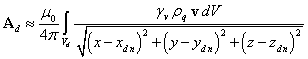Предположим теперь, что имеется некоторое множество зарядовых распределений, движущихся с разными постоянными скоростями в достаточно большом объёме пространства , неподвижном относительно системы отсчёта . В пределе непрерывно распределённых по объёму токов мы можем считать, что равняется сумме всех движущихся объёмов отдельных зарядовых распределений: .

Чтобы найти общий векторный потенциал, следует просуммировать векторные потенциалы от каждого зарядового распределения. Положим, что есть вектор от центра объёма до центра произвольного зарядового распределения, есть вектор от центра объёма до точки , так что . Обозначая , имеем , . Теперь сумма векторных потенциалов зарядовых распределений сводится к интегралу по неподвижному объёму :

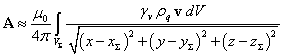. (8)

Величины , и обозначают координаты точек объёма и задаются относительно центра объёма .

Внутри каждого отдельного зарядового распределения в сопровождающей его системе отсчёта частицы обладают собственным хаотичным движением с некоторой скоростью . В этом случае с помощью векторного правила релятивистского сложения скоростей для абсолютной скорости и фактора Лоренца произвольной частицы в системе отсчёта находим:

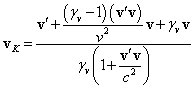, , (9)

где – фактор Лоренца для скорости , – фактор Лоренца для скорости , – фактор Лоренца для скорости .

Учёт хаотической скорости в (9) приводит к некоторому изменению скоростей частиц в , и в (8) вместо скорости следует подставить скорость . Но если использовать условие хаотичности движения заряженных частиц в и учесть большое количество этих частиц, можно упростить задачу путём определения усреднённых значений для и . При таком усреднении в выбранной точке внутри распределения частиц следует взять небольшой прилегающий к точке объём, содержащий достаточное количество частиц, и провести усреднение по времени и объёму. В первом приближении согласно (9) получается, что , . Тогда вместо в (8) следует подставить , и учесть определение для плотности тока :

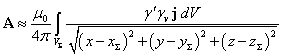. (10)

Чтобы найти компоненты векторного потенциала , следует взять три интеграла в (10), отдельно для каждой компоненты плотности тока . Величины , и являются функциями координат внутри неподвижного объёма . Однако лишь радиус-вектор , задающий положение точки относительно центра объёма , зависит от координат точки . Поэтому при вычислении магнитного поля по формуле операция ротора должна применяться только к величине .

Внося ротор под знак интеграла в (10), и учитывая равенство, имеем:

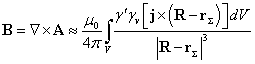. (11)

Выражения (11) и (1) совпадают по внешнему виду, учитывая, что . Если ещё в (11) положить , , не учитывая тем самым собственное хаотичное движение заряженных частиц внутри вещества и полагая малой скорость заряженных частиц по сравнению со скоростью света , то (11) переходит в (1). Таким образом, магнитное поле в законе Био–Савара–Лапласа (1) определяется с относительной неточностью, по порядку величины равной .

3. Вращательное движение зарядов

Пусть заряд вращается относительно некоторой оси с постоянной угловой скоростью на неизменном расстоянии от этой оси, равном . В момент времени линейная скорость вращения равна

где вектор

определяет положение заряда как функцию от цилиндрических координат , а также как функцию от времени. Величина обозначает начальную фазу, задающую компоненты при .

Пусть вектор связывает начало координат и точку , в которой требуется найти магнитное поле. Тогда вектор

будет вектором от заряженной частицы до точки в момент времени . Длина этого вектора равна:

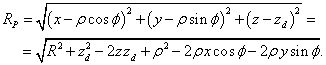
Согласно (4) ранний момент времени зависит от длины вектора , который является вектором , но взятым в ранний момент времени . Поскольку , , то для величин в раннее время находим:

, (12)

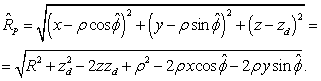(13)

Подставим в формулу Лиенара-Вихерта (3) для векторного потенциала за пределами движущейся точечной заряженной частицы вместо скорость вращения , и учтём, что :

Теперь необходимо просуммировать векторные потенциалы отдельных заряженных частиц. Пусть имеется некоторое вращающееся тело, содержащее множество близко расположенных заряженных частиц. Эти частицы могут ещё хаотически двигаться со скоростью в системе отсчёта , неподвижной относительно тела.

Для случая вращения фактор Лоренца в (9) следует заменить на , а скорость заменить на скорость вращения , После усреднения фактора Лоренца появляется его среднее значение . Элемент заряда вращающейся точечной частицы в цилиндрических координатах можно выразить через инвариантную плотность заряда , факторы Лоренца и , и через движущийся объём :

Здесь есть плотность заряда движущегося с фактором Лоренца заряженного вещества; вследствие Лоренцевского сокращения будет , где есть элемент объёма не вращающегося тела в цилиндрических координатах. С учётом этого сумма векторных потенциалов отдельных частиц преобразуется в интеграл по объёму тела:

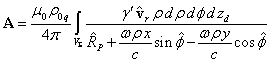Если учесть (12), то векторный потенциал вращающегося тела имеет две ненулевые компоненты:

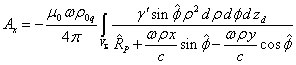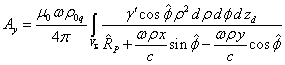. (14)

Магнитное поле находится по формуле . С учётом (14) вычислим компоненту магнитного поля:

Беря частные производные, находим:

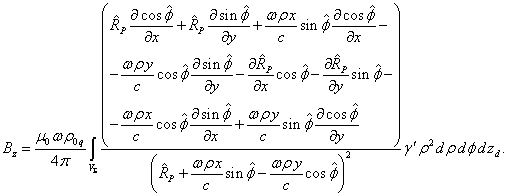
(15)

Из соотношений , , вытекает следующее:

, .

(16)

Следовательно, для частных производных можно записать:

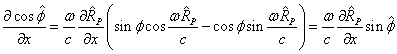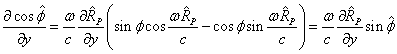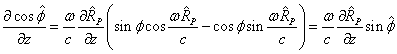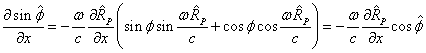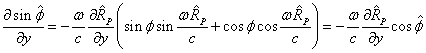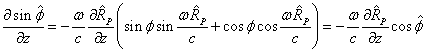. (17)

Подставим (17) в (15):

Из (13) и (17) находим:

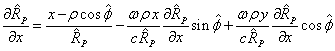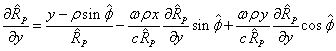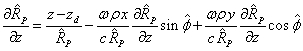Отсюда выражаем , и , а затем подставляем и в выражение для:

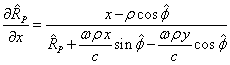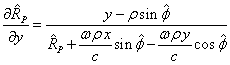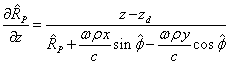. (18)

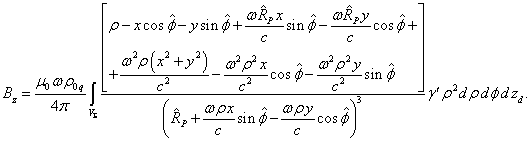
(19)

Вычисление компонент и оказывается проще, так как :

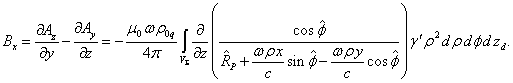
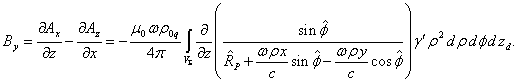
Используя (17) и (18), находим:

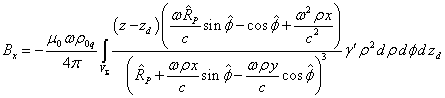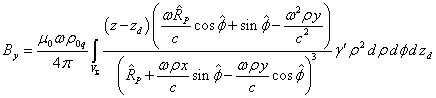. (20)

Поместим начало системы координат на ось вращения таким образом, чтобы ось совпала с осью вращения. Предположим теперь, что точка , где ищется магнитное поле, лежит на оси вращения. Тогда вектор от начала координат до точки будет равен , и согласно (13) будет . С учётом (16) для компонент магнитного поля (20) при находим:

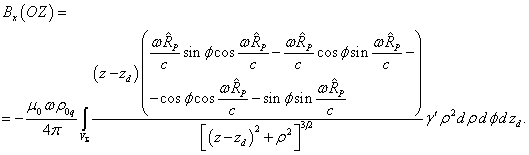
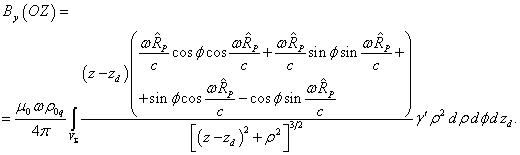
Если координата точки невелика, то это же можно сказать о величине . Мы можем считать тогда, что , и разложить и до членов второго порядка. Это упрощает выражения для и :

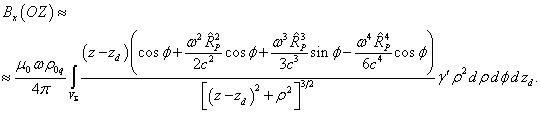
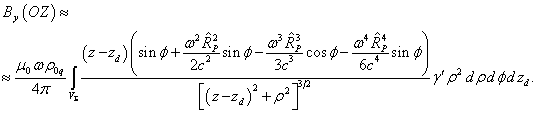
(21)

Предположим теперь, что вращающееся заряженное тело осесимметрично относительно оси . Тогда в (21) интегрирование по координатам и будет независимо от координаты . При этом интегрирование в (21) по координате в пределах от 0 до даст нуль, так что компоненты и на оси вращения становятся равными нулю.

Рассмотрим теперь компоненту в (19) на оси , где и равны нулю, при этом :

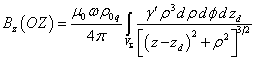. (22)

Мы видим, что подынтегральное выражение в формуле (22) для не содержит какую-либо явную функцию от переменной , кроме , при любом выборе оси вращения. В частности, ось вращения может быть и за пределами вращающегося заряженного тела.

Для осесимметричного тела относительно оси интегрирование по цилиндрическим переменным и получается не зависящим от . В этом случае интегрирование по переменной в пределах от 0 до даст просто . Для (22) получается тогда следующее:

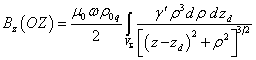. (23)

Таким образом, мы доказали следующую теорему: Магнитное поле на оси вращения осесимметричного заряженного тела или распределения зарядов имеет только одну компоненту, направленную вдоль оси вращения, причём магнитное поле выражается через интеграл по поверхности, не требующий интегрирования по азимутальному углу . В общем случае для произвольного распределения зарядов и при любом расположении оси вращения магнитное поле выражается через интеграл по объёму, в котором подынтегральное выражение не зависит от .

Выражение (23) можно переписать в сферических координатах, учитывая, что элемент объёма есть , кроме этого, , :

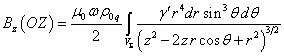. (24)

Отсутствие необходимости интегрирования в (23-24) по переменной упрощает вычисление магнитного поля на оси вращения осесимметричного распределения зарядов.

4. Магнитное поле на оси цилиндра

Применим (23) для вычисления магнитного поля на оси длинного твёрдого цилиндра с длиной , имеющего радиус и вращающегося с угловой скоростью . Предполагается, что до начала вращения данный цилиндр был однородно заряжен по всему объёму с плотностью заряда , а вращение не приводит к сдвигу зарядов за счёт центробежной силы. Для твёрдого цилиндра можно также положить фактор Лоренца и не учитывать тем самым собственное хаотическое движение заряженных частиц.

Помещая начало системы координат в центр цилиндра, из (23) находим:

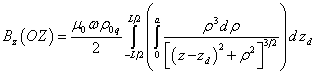. (25)

В (25) внутренний интеграл задаёт поле от тонкого вращающегося заряженного диска с радиусом , расположенного на расстоянии от центра цилиндра, а интеграл по переменной суммирует поля от всех тонких дисков, расположенных в пределах от до перпендикулярно оси .

За пределами цилиндра при и при результат интегрирования в (25) будет следующий:

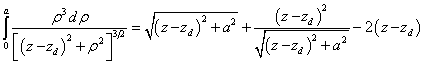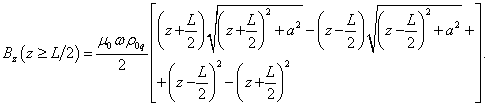
(26)

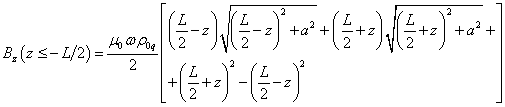(27)

Формула (27) получается из (26) путём замены на . Из (26-27) следует, что на торцах цилиндра, где либо , магнитное поле на оси одинаково и по величине равно

. (28)

Приблизительное значение в (28) соответствует случаю длинного цилиндра, у которого .

Найдём теперь магнитное поле внутри цилиндра. Пусть, например, . Рассечём цилиндр при таком плоскостью, перпендикулярной оси , и получим два новых цилиндра, длины которых будут равны соответственно и . Магнитное поле в точке на оси исходного цилиндра будет равно сумме магнитных полей на торцах двух новых цилиндров. Подставляя в (28) вместо длины и соответственно, и суммируя результаты, находим:

(29)

При магнитное поле (29) совпадает с полем (28) на торце цилиндра.

При из (29) следует магнитное поле в центре цилиндра:

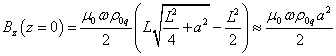Из сравнения с (28) видно, что поле в центре длинного цилиндра превышает почти в два раза поле на оси на торцах этого цилиндра. Такое различие связано с увеличением неоднородности поля на торцах цилиндра.

При больших , когда , можно разложить корни в (26) до членов второго порядка. В результате получим:

, (30)

так что поле на оси цилиндра при больших расстояниях убывает обратно пропорционально кубу расстояния до центра цилиндра.

4. Магнитное поле на оси шара

Пусть имеется однородно заряженный шар радиуса , с инвариантной объёмной плотностью заряда , вращающийся с угловой скоростью относительно оси . Для твёрдого шара можно считать, что фактор Лоренца заряженных частиц в системе отсчёта, жёстко связанной с шаром.

Вычислим вначале магнитное поле за пределами шара на оси . Если начало системы координат находится в центре шара, то для поля при и при согласно (24) можно записать:

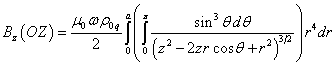. (31)

Из (31) следует:

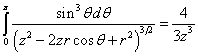, . (32)

В отличие от поля вдали от вращающегося длинного цилиндра в (30), внешнее поле на оси вращения шара в (32) начинает уменьшаться обратно пропорционально сразу же за пределами шара. На полюсе шара при магнитное поле будет равно .

Если положить в (31), находится поле в центре шара:

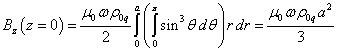Полученные оценки магнитного поля точно соответствуют значениям в [8].

5. Заключение

Исходя из выражений запаздывающих потенциалов Лиенара–Вихерта (Lienard–Wiechert) (3), мы выводим закон Био–Савара–Лапласа (Biot–Savart law) для магнитного поля в виде (11). Особенностью полученного выражения является то, что в нём учтено собственное хаотичное движение заряженных частиц внутри вещества. Это позволяет применить (11) для анализа электромагнитного поля в релятивистской однородной системе со свободно движущимися заряженными частицами.

Упрощения, сделанные при выводе (11) показывают, что закон Био–Савара–Лапласа имеет относительную неточность, по порядку величины равную . Здесь есть скорость света, обозначает среднюю скорость заряженных частиц в плотности тока , причём есть плотность заряда движущегося вещества.

От прямолинейно направленных токов мы переходим к стационарным круговым токам, создаваемых вращением зарядовых распределений, и снова используем потенциалы Лиенара–Вихерта. В результате мы приходим к теореме о магнитном поле вращающихся заряженных тел. Путём точного вычисления частных производных по координатам от векторного потенциала с учётом эффекта запаздывания, мы выводим формулы (22-24) для магнитного поля на оси вращения. Согласно доказанной теореме, магнитное поле при любом расположении оси вращения определяется интегралом по объёму зарядового распределения, причём подынтегральное выражение не зависит от угловой координаты . Для осесимметричных тел магнитное поле на оси вращения всегда направлено только вдоль этой оси, причём поле не зависит от , соответствуя симметрии этих тел.

С целью иллюстрации действия теоремы мы применяем её вначале к сплошному цилиндру, а затем к шару с учётом того, что оба тела вращаются и однородно заряжены по своему объёму. Формула (23) в цилиндрических координатах и формула (24) в сферических координатах позволяют быстро и точно определять внешнее магнитное поле вращающихся заряженных осесимметричных тел, а также поле в их центре. В иных случаях следует использовать общие формулы (21-22).

Доказанная теорема может также применяться как дополнительное средство для определения электромагнитных полей при решении волновых уравнений, позволяющее уточнить константы интегрирования и облегчить калибровку полученных решений для потенциалов и полей.

Список использованных источников

1. Feynman R., Leighton R. and Sands M. The Feynman Lectures on Physics. Vol. 2, Ch. 14 (1964). Addison-Wesley, Massachusetts, Palo Alto, London.

2. Daniel Zile and James Overdui. Derivation of the Biot-Savart Law from Coulomb’s Law and Implications for Gravity. APS April Meeting 2014, abstract id. D1.033. https://doi.org/10.1103/BAPS.2014.APRIL.D1.33.

3. David Tong. Lectures on Electromagnetism. University of Cambridge, Part IB and Part II Mathematical Tripos (2015). http://www.damtp.cam.ac.uk/user/tong/em.html.

4. Marsh J.S. Magnetic and electric fields of rotating charge distributions. American Journal of Physics, Vol. 50, Issue 1, pp. 51-53 (1982). https://doi.org/10.1119/1.13006.

5. Marsh J.S. Magnetic and electric fields of rotating charge distributions II. American Journal of Physics, Vol. 52, Issue 8, pp. 758-759 (1984). https://doi.org/10.1119/1.13852.

6. Lienard A. M. L’Éclairage électrique, Vol. 16, 5, 53, 106 (1898).

7. Wiechert E. Archives néerl., 2^nd series, Vol. 5, 549 (1900).

8. Griffiths D. J. Introduction to Electrodynamics, 3rd Edition; Prentice Hall, Upper Saddle River, New Jersey (2007).

Источник: http://sergf.ru/tm.htm

На научный сайт