На русском языке

Gravitational induction

Gravitational induction is a property of gravitational field to cause rotation of matter in a changing flux, of gravitomagnetic field in general relativity, and of gravitational torsion field in Lorentz-invariant theory of gravitation and covariant theory of gravitation.

1 Theory of phenomenon
2 Typical cases
3 Differential approach
4 Application in physics
5 References
6 See also
7 External links

Theory of phenomenon

One of the four equations of Lorentz-invariant theory of gravitation (see also gravitomagnetism and Maxwell-like gravitational equations) has the following form: ^[1]

$~ \nabla \times \mathbf{\Gamma } = - \frac{\partial \mathbf{\Omega} } {\partial t}, \qquad\qquad (1)$

where:

$~ \mathbf{\Gamma }$ is gravitational field strength,
$~\mathbf{\Omega}$ is gravitational torsion field.

According to $(1)$ , after a change in time of $~\mathbf{\Omega}$ there appear circular field (rotor) of $~ \mathbf{\Gamma }$ , having the opportunity to lead matter in rotation.

If the vector of torsion $~\mathbf{\Omega}$ crosses a certain surface , then we can calculate the flux of this field through this surface:

$~\Phi = \int \mathbf{\Omega}\cdot \mathbf{n }ds, \qquad\qquad (2)$

where $~\mathbf{n}$ – the vector normal to the element of surface .

Let’s take the partial derivative in equation $(2)$ with respect to time with the minus sign and integrate over the surface, taking into account the equation $(1)$ :

$~ -\int \frac{\partial \mathbf{\Omega} }{\partial t} \cdot \mathbf{n }ds = -\frac{\partial \Phi }{\partial t}= \int [\nabla \times \mathbf{\Gamma }] \cdot \mathbf{n }ds = \int \mathbf{\Gamma }\vec d\ell. \qquad\qquad (3)$

In the integration was used Stokes' theorem, replacing the integration over a surface of the curl of vector on the integration of this vector over the boundary of the surface. In the right side of $(3)$ is a term, equal to the work on transfer of a unit mass of matter on closed path $~\ell$ , bounding the surface . By analogy with electromagnetism, this work could be called gravitomotive force. In the middle of $(3)$ is time derivative of the flux $~\Phi$ . According to $(3)$ , gravitational induction occurs when the flux of field through a certain surface changes and is expressed in occurrence of rotational forces acting on particles of matter.

Gravitational induction can be regarded as gravitational analogue of the law of electromagnetic induction. ^[2] ^{[3] [4]}

Typical cases

Just as in electromagnetism, there are two different cases of gravitational induction. In the first case the flux $~\Phi$ is changed due to variable $~\mathbf{\Omega}$ with a constant flow surface, bounded by a loop.

In the second case, the torsion $~\mathbf{\Omega}$ remains constant, but the flux $~ \Phi$ changes due to changes in the area occupied by the matter of the loop. For example, consider rubber hose filled with liquid and arranged in a closed rectangular loop in the torsion field $~\mathbf{\Omega}$ . Let the three sides of the loop are fixed, while the fourth side extends with speed $~\mathbf{V}$ , increasing the area of the loop. Since the flux $~ \Phi$ through the loop changes, the liquid in the hose begins to circulate. The direction of motion of the fluid will be such that torsion field $~\mathbf{\Omega^\prime }$ of the fluid will be sent in the same direction as initial torsion field created the circulation of fluid (this is contrary to the Lenz's_law in electromagnetism).

The second case, with expanding of the loop, can also be considered using the expression for full gravitational force:

$~\mathbf{F}_{m} = m \left( \mathbf{\Gamma } + \mathbf{V} \times \mathbf{\Omega} \right), \qquad\qquad (4)$

where:

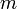– the mass of the fluid particles on which the force is acting,
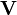$~ \mathbf{V}$ – the particle velocity as the velocity of stretching of the loop.

From $(4)$ for the unit mass, located only in torsion field $~\mathbf{\Omega}$ , should:

$~\mathbf{\Gamma_{S }} =\mathbf{V} \times \mathbf{\Omega}. \qquad\qquad (5)$

The integral of field strength $(5)$ around the contour of the loop gives gravitomotive force, as the work of gravitational force on the displacement of unit mass. This integral will be:

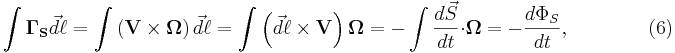
$~ \int \mathbf{\Gamma_{S }} \vec d\ell = \int \left( \mathbf{V} \times \mathbf{\Omega}\right) \vec d\ell =\int \left( \vec d\ell \times \mathbf{V}\right) \mathbf{\Omega}=-\int \frac {d\vec S}{dt}\cdot \mathbf{\Omega}=-\frac {d\Phi_S}{dt}, \qquad\qquad (6)$

where $~d\vec S$ is the vector describing change in the area of the loop during time , arises due to the movement of one side of the loop $~ d\ell$ in the direction of velocity $~ \mathbf{V}$ .

Expression (6) is the rate of change of the flux of torsion field when the contour of the area changes. Comparing $(3)$ , $(5)$ and $(6)$ we find for the induced field strength: $~ \mathbf{\Gamma_{S }}= \mathbf{V}\times \mathbf{\Omega}$ . Thus, during of changing the flux $~\Phi$ liquid inside the hose comes in motion and begins to circulate in the direction specified by the vector of induced field strength $~ \mathbf{\Gamma_{S }}$ . Gravitational induction regards to the matter of the hose too, so that if the hose is not attached, it will rotate synchronously together with its contents.

At first glance, it is unclear why the effect of gravitational induction in the form of rotation of matter is caused by two different phenomena - either a change in amplitude of torsion field, or a change in area of the circuit through which the torsion field passes. The answer can be found in the article, ^[5] where the integral equations of electromagnetic field in curved space-time were considered. In this article, it is shown that electromotive force in the circuit is determined by the strength of vortex electric field, which occurs when magnetic flux through the circuit changes. With regard to the electric field strength, it is known that it can arise when vector potential of electromagnetic field changes over time, which is what happens when magnetic field in the circuit changes over time. If any part of the circuit begins to move and cross the magnetic field lines, then an electric field strength arises in this part of the circuit, regardless of whether there are electric charges in the circuit matter or not. This follows from transformation of electromagnetic field tensor components from a stationary reference frame to a moving reference frame associated with the moving part of the circuit. Thus, in a conducting circuit that changes its area due to compression or stretching, an electromotive force of electromagnetic induction arises, and an explanation with the Lorentz force is not required. Hence, in view of similarity of electromagnetic and gravitational phenomena, the effect of gravitational induction becomes clear.

Differential approach

The theory of phenomena of gravitational induction can be explained also by means of differential quantities. ^[6] If we assume that the flux of torsion field instead of (2) is determined by the expression $~\Phi = \mathbf{\Omega}\cdot \mathbf{S}$ , where $~ \mathbf{S}=\mathbf{n} S$ is the vector of a certain small area, and torsion $~ \mathbf {\Omega}$ is homogeneous in this area, then the rate of change of the flux of torsion field can be written:

$~ - \frac{\partial \Phi }{\partial t} = - \frac{\partial \mathbf{\Omega} }{\partial t} \cdot \mathbf{S}- \mathbf{\Omega} \frac{\partial \mathbf{S} }{\partial t}.$

Substituting (1) and (6):

$~ - \frac{\partial \Phi }{\partial t} = [\nabla \times \mathbf{\Gamma }] \cdot \mathbf{S} + [\mathbf{V} \times \mathbf{\Omega}] \cdot \vec \ell =- \frac{\partial \Phi_{\Omega}}{\partial t} - \frac{\partial \Phi_{S}}{\partial t}.$

From this, taking into account (3) in the general case follows:

$~ - \frac{\partial \Phi_{\Omega}}{\partial t} = - \frac{\partial \mathbf{\Omega} }{\partial t} \cdot \mathbf{S} = \int \mathbf{\Gamma_{\Omega}}\vec d\ell.$

$~ - \frac{\partial \Phi_{S}}{\partial t} = - \mathbf{\Omega}\cdot \frac{\partial \mathbf{S} }{\partial t} = \int \mathbf{\Gamma_{S}}\vec d\ell.$

so in the case of changing of field torsion $~\mathbf{\Omega}$ , or in the case of changing of vector of area $~\mathbf{S}$ when contour is intersecting the torsion field, the flux of torsion field is changing and gravitomotive force is creating. When the vector of area is changing gravitomotive force arises in the sides of the loop, which move at the speed $~ \mathbf{V}$ crossing lines of torsion field. The direction of the force acting on matter of the loop is determined by vector product $~ \mathbf{V} \times \mathbf{\Omega}$ .

Application in physics

In covariant theory of gravitation (CTG) gravitational stress-energy tensor has the form: ^[6]^[7]

$~U^{{ik}}={\frac {c^{2}}{4\pi G}}\left(-g^{{im}}\Phi _{{mr}}\Phi ^{{rk}}+{\frac {1}{4}}g^{{ik}}\Phi _{{rm}}\Phi ^{{mr}}\right)$ ,

where – speed of light, – gravitational constant, $~ g^{ik}$ – metric tensor, and gravitational tensor is calculated through gravitational four-potential $~D_{i}=\left({\frac {\psi }{c}},-{\mathbf {D}}\right)$ as follows:

$~\Phi_{ik}= \nabla _{i} D_{k}- \nabla_{k} D_{i} = \partial_{i} D_{k}-\partial_{k} D_{i}$ .

In weak field approximation, when the curvature of spacetime can be set almost equal to zero, the equations of CTG become close to equations of Lorentz-invariant theory of gravitation. This causes the wave equations ^[8] ^[9] for potentials of gravitational field ( $~\psi$ – scalar potential, $~ \mathbf{D}$ – vector potential), and for field strength $~ \mathbf{\Gamma }$ and torsion (gravitomagnetic) field $~ \mathbf{\Omega}$ . In stationary case, the wave equations of gravitational field become Poisson's equations of classical physics. In this approximation time-like components of gravitational stress-energy tensor can be written explicitly:

$~U^{{00}}=-{\frac {1}{8\pi G}}(\Gamma ^{2}+c^{2}\Omega ^{2})$ – energy density of gravitational field,

$~U^{{0k}}={\frac {1}{c}}H^{k}$ , where index and $~H^{k}={\mathbf {H}}=-{\frac {c^{2}}{4\pi G}}[{\mathbf {\Gamma }}\times {\mathbf {\Omega }}]$ is the vector of energy flux density of gravitational field or Heaviside vector.

Negative energy density and energy flux lead to unique property inherent to gravitational field. This property lies in the fact that the gravitational effect of induction between two masses under certain conditions is not damped, and may increase in amplitude, as in systems with positive feedback. For example, if two bodies are attracted by gravitation and rotate in the same direction, then the change of potential energy of gravitational field will transform into rotational energy of the bodies through gravitational induction. Thus, the bodies will rotate each other, increasing torsion field $~\mathbf{\Omega }$ around them.

Described mechanism is proposed to explain the nuclear forces between nucleons in atomic nuclei in gravitational model of strong interaction. ^[6] With proper arrangement of nucleons in nucleus due to the gravitational induction nucleons spin up to a maximum angular velocity. The result is a repulsive force of nucleons spins (in gravitoelectromagnetism these forces are called gravitomagnetic forces) of such magnitude that are enough to compensate the force of attraction of the nucleons from the field of strong gravitation. In such evaluating of the forces acting in atomic nuclei, is used strong gravitational constant.^[10]

References

Fedosin S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik, Perm, (1999-06-09) 544 pp. ISBN 5-8131-0012-1.
Einstein, Albert. 1912. “Gibt es eine Gravitationswirkung die der elektrodynamischen Induktionswirkung analog ist?” Vierteljahrsschrift für gerichtliche Medizin und öffentliches Sanitätswesen, 44: 37–40.
Myron W. Evans. Gravitational equivalent of the Faraday Law of Induction. Paper 75. Alpha Institute for Advanced Studies (AIAS).
C.J. de Matos, M. Tajmar. Gravitational Poynting Vector and Gravitational Larmor Theorem in Rotating Bodies with Angular Acceleration. 4 Jul 2001, arXiv:gr-qc/0107014v1.
Fedosin S.G. On the Covariant Representation of Integral Equations of the Electromagnetic Field. Progress In Electromagnetics Research C, Vol. 96, pp. 109-122 (2019). https://doi.org/10.2528/PIERC19062902.
^4.0 ^4.1 ^4.2 Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X.
Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron, Vol. 14, No. 4, P. 385-413, 2007; paper in Russian: Электромагнитная и гравитационная картины мира.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).

External links

Gravitational induction in Russian

Source: http://sergf.ru/gien.htm

On the list of pages