На русском языке

 

Selfconsistent gravitational constants

 

From Wikiversity

 

Self-consistent gravitational constants are complete sets of fundamental constants, which are self-consistent and define various physical quantities associated with gravitation. These constants are calculated in the same way as electromagnetic constants in electrodynamics. This is possible because in the weak field equations of general relativity are simplified into equations of gravitoelectromagnetism, similar in form to Maxwell's Equations. Similarly, in the weak field approximation equations of covariant theory of gravitation [1] turn into equations of Lorentz-invariant theory of gravitation (LITG). LITG equations are Maxwell-like gravitational equations, which are similar to equations of gravitoelectromagnetism. If these equations are written with the help of self-consistent gravitational constants, there is the best similarity of equations of gravitational and electromagnetic fields. Since in 19-th century there was no International System of Units, the first mention of gravitational constants was possibly due to Forward (1961).[2]

Contents

  • 1 Definition
  • 2 Connection with Planck mass and Stoney mass
  • 3 Connection with fine-structure constant
  • 4 Strong gravitational torsion flux quantum
  • 5 See also
  • 6 References
  • 7 External links

Definition

In gravitational wave representation, the set of gravitational constants depends on the speed of propagation of gravity, in contrast to electromagnetic wave representation, in which all space-time measurements and definition of physical quantities are based on the speed of light.

Primary set of gravitational constants is:

1. First gravitational constant: ~c_g , which is the speed of gravitational waves in vacuum; [3]

2. Second gravitational constant: ~\rho_{g} , which is the gravitational characteristic impedance of free space.

Secondary set of gravitational constants is:

1. Gravitoelectric gravitational constant (like electric constant): ~\varepsilon_g = \frac{1}{4\pi G } = 1.192708\cdot 10^9 \mathrm {kg \cdot s^2 \cdot m^{-3}},  where ~ G  is gravitational constant.

2. Gravitomagnetic gravitational constant (like vacuum permeability):   ~\mu_g = \frac{4\pi G }{ c^2_{g}}.    If the speed of gravitation is equal to the speed of light, ~ c_{g}=c,   then [4]   ~\mu_{g0} = 9.328772\cdot 10^{-27} \mathrm {m / kg}.

Both, primary and secondary sets of gravitational constants are selfconsistent, because they are connected by the following relationships:

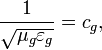
~\frac{1}{\sqrt{\mu_g\varepsilon_g}} = c_g ,                   ~\sqrt{\frac{\mu_g}{\varepsilon_g}} = \rho_{g} = \frac{4\pi G }{c_g}. 

If  ~ c_{g}=c,   then gravitational characteristic impedance of free space be equal to: [5] [6]

~ \rho_{g0} = \frac{4\pi G }{c} =2.796696\cdot 10^{-18} \mathrm {m^2/(s\cdot kg)}.  

In Lorentz-invariant theory of gravitation the constant  ~ \rho_g    in case ~c_{{g}}=c is contained in formula for vector energy flux density of gravitational field (Heaviside vector): [3]

~{\mathbf {H}}=-{\frac {c^{2}}{4\pi G}}{\mathbf {\Gamma }}\times {\mathbf {\Omega }}=-{\frac {c}{\rho _{{g0}}}}{\mathbf {\Gamma }}\times {\mathbf {\Omega }}, 

where:

§   ~ \mathbf{\Gamma }  is gravitational field strength,

§  ~ \mathbf{\Omega}  is gravitational torsion field.

 

For plane transverse uniform gravitational wave, in which for amplitudes of field strengths holds ~\Gamma = c_g \Omega according to Maxwell-like gravitational equations,  may be written:

~H = \frac{ \Gamma^2 }{\rho_g }. 

A similar relation in electrodynamics for amplitude of flux density of electromagnetic energy of a plane electromagnetic wave in vacuum, in which  ~ E = c B , is as follows: [7]

~S = \frac{ E^2 }{Z_0 },

where  ~ \mathbf {S} = \frac {\mathbf{E}\times \mathbf{B} }{\mu_0} = \frac {c}{Z_0}\mathbf{E}\times \mathbf{B}   –  Poynting vector, ~ E   – electric field strength, ~ B   – magnetic flux density,

 ~ \mu_0   – vacuum permeability, ~ Z_0 = c \mu_0   – impedance of free space.

 

Gravitational impedance of free space  ρ g 0 {\displaystyle ~\rho _{g0}}  ~\rho _{{g0}}  was used in paper [8] to evaluate the interaction section of gravitons with matter.

Connection with Planck mass and Stoney mass

Since gravitational constant and speed of light are included in Planck mass  m_P = \sqrt{\frac{\hbar c}{ G }}\ ,  where ~ \hbar  – reduced Planck constant or Dirac constant, then gravitational characteristic impedance of free space can be represented as:

~ \rho_{g0} = \frac{2h}{m_{P}^2} ,

where ~ h  – Planck constant.

There is Stoney mass, related to elementary charge  ~ e   and electric constant  ~ \varepsilon_0:

~m_S = e\sqrt{\frac{\varepsilon_g}{\varepsilon_0}} = \frac{e}{\sqrt{4\pi G \varepsilon_0}} .

Stoney mass can be expressed through the Planck mass:

~m_S = \sqrt{\alpha}\cdot m_P ,

where  ~ \alpha     is the electric fine-structure constant.

This implies another expression for gravitational characteristic impedance of free space:

~ \rho_{g0} = \alpha \cdot \frac{2h}{m_{S}^2} .

Newton law for gravitational force between two Stoney masses can be written as:

~F_g = \frac{1}{4\pi \varepsilon_g}\cdot \frac{m_{S}^2}{r^2}= \alpha_g \cdot \frac{\hbar c}{r^2}.

Coulomb's law for electric force between two elementary charges is:

~F_e = \frac{1}{4\pi \varepsilon_0}\cdot \frac{e^2}{r^2}= \alpha \cdot \frac{\hbar c}{r^2}.

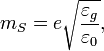Equality of ~F_g  and ~F_e  leads to equation for the Stoney mass ~m_S = e\sqrt{\frac{\varepsilon_g}{\varepsilon_0}},    that was stated above. Hence the Stony mass may be determined from the condition that two such masses interact via gravitation with the same force as if these masses had the charges equal to the elementary charge and only interact through electromagnetic forces.

Connection with fine structure constant

The electric fine structure constant is:

~\alpha = \frac{e^2}{2\varepsilon_0 hc}.

We can determine the same value for gravitation so: ~\alpha_g = \frac{m_{S}^2}{2\varepsilon_g hc}=\alpha ,   with the equality of the fine structure constants for both fields.

On the other hand, the gravitational fine structure constant for hydrogen system at the atomic level and at the level of star is also equal to fine structure constant:

~\alpha ={\frac {G_{s}M_{p}M_{e}}{\hbar c}}={\frac {GM_{{ps}}M_{{\Pi }}}{\hbar _{s}C_{s}}}={\frac {1}{137,036}},

where  ~G_{s}  – strong gravitational constant, ~M_p   and  ~M_e   – the mass of proton and electron, ~ M_{ps}   and  ~ M_{\Pi }   – mass of the star-analogue of proton and the planet-analogue of electron, respectively, ~ \hbar_s   – stellar Dirac constant, ~ C_s   – characteristic speed of stars matter.

Strong gravitational torsion flux quantum

The magnetic force between two fictitious elementary magnetic charges is:

F_m = \frac{1}{4\pi \mu_0}\cdot \frac{ q_m^2}{r^2} = \beta \cdot \frac{\hbar c}{r^2}, \

 

where   q_m = \frac{h}{e} \   is the magnetic charge,  \beta = \frac {\varepsilon_0 h c}{2 e^2} = \frac {\pi \hbar}{c \mu_0 e^2}  is the magnetic coupling constant for fictitious magnetic charges. [9] 

The force of gravitational torsion field between two fictitious elementary torsion masses is:

 

F_{\Omega} = \frac{1}{4\pi \mu_{g0}}\cdot \frac{m_{\Omega }^2}{r^2} = \beta_g\cdot \frac{\hbar c}{r^2}, \

 

where  \beta_g = \frac {\varepsilon_g h c}{2 m_S^2} = \frac {\pi \hbar}{c \mu_{g0} m_S^2} \   is gravitational torsion coupling constant for gravitational torsion mass   m_{\Omega } \ .

In case of equality of the above forces, we shall get the equality of the coupling constants for magnetic field and gravitational torsion field:

\beta = \beta_g = \frac{1}{4\alpha}, \

from which Stoney mass   m_S \   and gravitational torsion mass could be derived:

 

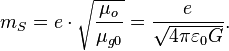
m_S = e \cdot \sqrt {\frac{\mu_o}{\mu_{g0}}} = \frac{e}{\sqrt {4 \pi \varepsilon_0 G}}. \

 

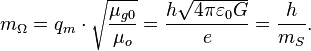
m_{\Omega } = q_m \cdot \sqrt {\frac{\mu_{g0}}{\mu_o }} = \frac{h \sqrt {4 \pi \varepsilon_0 G}}{e }=\frac {h}{m_S} . \

 

Instead of fictitious magnetic charge   q_m= h/e   the single magnetic flux quantum  Φ0 = h/(2e) ≈2.067833758(46)×10−15
 Wb [10] has the real meaning in quantum mechanics. On other hand at level of atoms the strong gravitation operates and we must use strong gravitational constant. So, we believe that the strong gravitational torsion flux quantum there should be important:

 

\Phi _{\Gamma }={\frac {h}{2e}}{\sqrt {{\frac {4\pi \varepsilon _{0}G_{s}M_{e}}{M_{p}}}}}={\frac {h}{2M_{p}}}=1,98\cdot 10^{{-7}}   m2/s,

 

which is related to proton with its mass  M_p   and to its velocity circulation quantum.

See also

References

  1. Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
  2. R. L. Forward, Proc. IRE 49, 892 (1961).
  3. 3.0 3.1Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1. 
  4. Kiefer, C.; Weber, C. On the interaction of mesoscopic quantum systems with gravity. Annalen der Physik, 2005, Vol. 14, Issue 4, Pages 253 – 278.
  5. J. D. Kraus, IEEE Antennas and Propagation. Magazine 33, 21 (1991).
  6. Raymond Y. Chiao. "New directions for gravitational wave physics via “Millikan oil drops”, arXiv:gr-qc/0610146v16 (2007).PDF
  7. Иродов И.Е. Основные законы электромагнетизма. Учебное пособие для студентов вузов. 2- издание. М.: Высшая школа, 1991.
  8. Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, P. 1 – 18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
  9. Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kiev: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu.
  10. "Magnetic flux quantum Φ0". 2010 CODATA recommended values. Retrieved 10 January 2012.

External links

 

Source: http://sergf.ru/sken.htm

On the list of pages