Substantial neutron model

The substantial neutron model is a theoretical model describing the internal structure, origin and evolution of the neutron based on the theory of Infinite Hierarchical Nesting of Matter and the theory of similarity of matter levels.

1 Electromagnetic structure

1.1 Stellar model
1.2 Neutron

2 Beta decay
3 Origin
4 References
5 See also
6 External links

Electromagnetic structure

Neutrons and protons are collectively called nucleons and they are the constituents of atomic nuclei. A neutron and a proton are very close to each other by their mass, they have the same spin, but a neutron, in contrast to a proton, is neutral. Despite the lack of the electric charge, a neutron has a magnetic moment, which reflects its complex internal structure. The neutron’s magnetic moment is directed oppositely to the spin, while the proton’s magnetic moment and the spin are directed in the same way.

In order to study the structure of nucleons, the experiments were conducted on scattering the high-energy (up to 20 GeV) electron beams on liquid hydrogen and on deuterium, the nuclei of which include neutrons in addition to protons. ^[1] ^[2] ^[3] The experiments’ interpretation allowed scientists to estimate the sizes of nucleons, as well as the spatial distribution of charges and magnetic moments of the proton and neutron. It follows from the results that the nuclear core of the neutron can be positively charged and its periphery is negatively charged. The complex structure of the neutron can also be seen from its mass value as compared to the proton mass. If we assume that the proton, in a certain respect, is a charged neutron, then its mass must differ from the neutron mass due to the charge’s contribution into the total mass-energy. It turns out that not only the neutron is more massive than the proton, but in most of the identical quasi-stable particles the neutral particle is more massive than the positively charged one. For example, Σ⁺ is lighter than Σ⁰, and Σ⁰ is lighter than Σ^–.

Stellar model

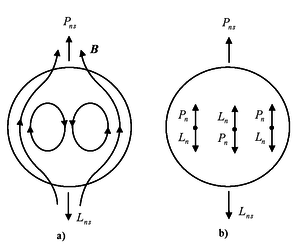
The structure of the magnetic field of a neutron star. a) The magnetic lines with induction in the model of a neutron star, which is the analogue of a neutron. $~P_{ns},$ $~L_{ns}$ are the magnetic moment and the spin of the star. b) The orientation of the magnetic moments and spins of the neutrons in the equatorial plane; in the center and in the shell of the star the magnetic moments $~P_{n}$ of the neutrons are opposite.

As an enlarged model of the neutron we consider the neutron star, which was formed in the matter collapse during the supernova explosion. In the Figure (a) the magnetic lines with induction are shown; $~P_{ns}$ and $~L_{ns}$ indicate the magnetic moment and the spin of the star. The orientation of the magnetic moments and spins of the neutrons in the equatorial plane is shown in Figure (b); in the center and in the shell of the star the magnetic moments $~P_{n}$ of the neutrons are opposite.

The matter of such a star consists mainly of neutral neutrons with a certain number of protons and electrons. It is assumed that during formation of a neutron star the electric charge density gradient is produced, with predominance of the positive charge at the center and some excess of electrons near the surface. The charge separation may occur, for example, as a consequence of the rapid matter collapse in the supernova and the effect of voluminous thermoelectromotive force, when the electrons tend to move from the center of the star with a high temperature to the surface, which has a lower temperature due to cooling. ^[4] This is the key principle in the electrokinetic magnetic model, in which the primary magnetic field of cosmic bodies (planets and stars) arises due to charge separation and rotation of these bodies, after which the field is also maintained by magnetically ordered matter, as is the case in the permanent magnets. ^[5]

If for the total charge density inside the star we take the linear dependence of the form:

$~\rho _{q}=\rho _{1}+hr,$

where $~\rho _{1}$ is the charge density in the center, is a certain coefficient, is the current radius, then from the condition of electroneutrality of the neutron star, which is the neutron’s analogue, and the integral of the charge density over the star volume it follows:

$~\int \rho _{q}\,dV=0,$

$~h=-{\frac {4\rho _{1}}{3R_{s}}},$

where $~R_{s}$ is the radius of the star.

The estimation of the $~\rho _{1}$ quantity can be done in the following way. In the substantial proton model it is shown that the magnetic moment of the proton can be calculated based on the limiting rotation of its volume electric charge. Similarly, we can find the magnetic moment of the neutron, as well as the magnetic moment of the corresponding neutron star. To do this, according to the theory of similarity of matter levels we need to multiply the neutron’s magnetic moment $~P_{n}$ by the coefficients of similarity: in size $~P=1.4\cdot 10^{19},$ in mass $~\Phi =1.62\cdot 10^{57}$ and in velocity $~S=2.3\cdot 10^{-1},$ raised to the necessary power:

$~P_{s}=P_{n}(P^{1,5}\Phi ^{0,5}S^{2})=-1.1\cdot 10^{30}$ J/T.

On the other hand, the magnetic moment $~P_{s}$ of the neutron star, rotating at the angular velocity $~\omega$ , is found by integrating the volume charge density distribution over the volume of the star:

$~P_{s}=-{\frac {\rho _{1}V_{s}\omega R_{s}^{2}}{45}},$

where $~V_{s}$ is the volume of the star.

The limiting value of the angular velocity $~\omega$ of the star’s rotation can be approximately estimated using the equality of the gravitation force and the centripetal force at the equator:

$~{\frac {GM_{s}}{R_{s}^{2}}}=\omega ^{2}R_{s},$

where is the gravitational constant.

Using the value $~P_{s}$ , at the mass of the neutron star $~M_{s}=2.7\cdot 10^{30}$ kg, we determine the value $~\rho _{1}=4.6\cdot 10^{6}$ C/m³.

Since now we know the dependence $~\rho _{q}$ on the current radius, then by solving the Poisson Equation we can find the distribution of the potential and the electric field strength inside the star: ^[4]

$~\varphi ={\frac {\rho _{1}R_{s}^{2}}{18\varepsilon _{0}}}-{\frac {\rho _{1}r^{2}}{6\varepsilon _{0}}}+{\frac {\rho _{1}r^{3}}{9R_{s}\varepsilon _{0}}},$

$~E={\frac {\rho _{1}r}{3\varepsilon _{0}}}-{\frac {\rho _{1}r^{2}}{3R_{s}\varepsilon _{0}}},$

where $~\varepsilon _{0}$ is the electric constant.

Meanwhile, on the surface of a generally neutral neutron star the electric potential and the electric field strength are equal to zero. Here the excess electrons are almost at equilibrium because the attraction force from the positive volume charge at the center of the star is compensated by the force of electric repulsion of the electrons from one another.

The star can be considered as a spherical capacitor, the center of which is positively charged, and the outer shell is negatively charged. The extremum of the electric field strength is achieved in the middle of the star’s radius, where the volume charge changes its sign.

It is generally accepted that after formation young neutron stars rotate very fast, and then they gradually slow down due to energy losses for synchrotron radiation. Because of the above-mentioned charge separation at the stage of rapid rotation, the star may have the following structure of the magnetic field: in the direction from the center along the rotation axis to the poles the magnetic field is directed the same way as the angular velocity of the star’s rotation; the magnetic moments of nucleons and electrons are aligned along the field and maintain it; near the star's surface the magnetic field changes its direction to the opposite due to the rapid rotation of the excess electrons, located there, with corresponding location of the magnetic moments of nucleons and electrons. As a result, compensation of part of the star’s magnetic field takes place, some magnetic lines get closed within the space between the center and the shell of the star, and the total magnetic moment becomes negative. This picture of the magnetic field is mostly preserved after deceleration of the neutron star’s rotation, maintained by the magnetic moments of the nucleons ordered, in turn, by the magnetic field.

Neutron

The magnetic field structure of the neutron star, which is shown in the Figure, corresponds to the magnetic field structure accepted in the substantial model of the neutron. It is assumed that in the neutron’s matter, as well as in the neutron star, charge separation is carried out with a radial gradient of the electric charge. The center of the neutron is positively charged, the shell is negatively charged, and the total charge is zero. According to the formulas, given above for the neutron star, the charge distribution inside the neutron in the linear approximation has the form:

$~\rho _{q}=\rho _{1}\left(1-{\frac {4r}{3R_{n}}}\right),$

Where $~\rho _{1}={\frac {45P_{n}}{V_{n}{\sqrt {\Gamma M_{n}R_{n}}}}},$

$~P_{n},$ $~M_{n},$ $~V_{n}$ and $~R_{n}$ are the magnetic moment, mass, volume and radius of the neutron, $~\Gamma$ is the strong gravitational constant.

Knowing the electric charge distribution, we can find the electric and magnetic fields inside the neutron depending on the radius and the field energies. The energy of the neutron’s electric field is concentrated inside its volume and is almost three times less than that of the proton.

Beta decay

For about $~t_{n}=15$ minutes free neutrons are transformed into protons in $\beta ^{-}$ -decay (see the beta decay). In this process an electron and an electron antineutrino are emitted:

$n^{0}\rightarrow p^{+}+e^{-}+{\bar {\nu }}_{e}.$

Based on the described above, the neutron decay is considered as the result of the neutron’s matter instability relative to the gravitational field of strong gravitation, binding the neutron’s matter, and of the changes in the electromagnetic field structure, caused by the transformation of the neutron’s matter. The neutron lifetime can be converted to the lifetime of the corresponding neutron star before its transformation into a magnetar (which is the stellar analogue of the proton). To this end, according to the theory of similarity, we must multiply $~t_{n}$ by the coefficient of similarity in time $~\Pi =6.1\cdot 10^{19}.$ This gives a huge period of time of about 2•10¹⁵ years.

In $\beta ^{-}$ -decay of the neutron the energy of the antineutrino does not exceed $~E_{\nu }=782$ keV. Using the uncertainty principle we can calculate the shortest time of the antineutrino emission: $~\tau _{\nu }={\frac {\hbar }{E_{\nu }}}=8.4\cdot 10^{-22}$ s (here $~\hbar$ is the Dirac constant). Accordingly, in transformation of a neutron star into a magnetar we should expect ejection of part of the shell (containing magnetic ions, such as iron, and therefore magnetized) as well as polarized emission of a stellar electron antineutrino $~{\bar {\nu }}_{es}$ during a period exceeding $~\tau _{s}=\Pi \tau _{\nu }=0.05$ s. Polarization of the neutrino emission arises due to the stellar matter orientation by the magnetic field.

In the initial state we can assume that the neutron star, the analogue of the neutron, consists of two phases of matter. At the center of the star there is α–phase of matter consisting of nucleons, oriented by the magnetic field with respect to the star’s spin in the same way as in a magnetar. In the stellar shell there is β–phase consisting of nucleons with an increased proportion of electrons relative to the α–phase. The magnetic moment of the β–phase is opposite to the magnetic moment of the α–phase and it is larger in magnitude. This results in the negative value of the total magnetic moment of the star with respect to the spin, similarly to the neutron. At the same time, the negative charge of the β–phase matter compensates the positive charge of the α–phase, which gives zero charge of the star. In the stellar matter the following reactions take place, which involve the weak interaction with electrons:

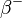$\beta ^{-}$ -decay of a neutron into a proton and an electron with emission of an electron antineutrino.
The reverse reaction – electron capture by protons with production of a neutron and emission of an electron neutrino:

$p^{+}+e^{-}\rightarrow n^{0}+\nu _{e}$ .

If the first reaction takes place in the stellar interior, the antineutrino flies away, the proton remains in place, bound by the pressure of matter and the magnetic field, and the electron with excessive kinetic energy from the decay reaction will move along the magnetic lines. As the electrons are diffusing from the center of the star to its surface, the possibility of the second reaction for these electrons is decreasing due to the pressure drop in the surrounding matter. Therefore, near the stellar surface we can expect increase in electrons’ concentration over time. In addition, electrons and other charged particles with excess energy have the possibility to fly away from the stellar surface to the magnetosphere and be accumulated there.

The neutrons in the shell of the neutron star also undergo $\beta ^{-}$ -decay in reaction 1, transforming into protons. It can be assumed that due to preserving the nucleon spin direction in the process of $\beta ^{-}$ -decay, transformation of each neutron into a proton leads to a change in the sign of the magnetic moment (the magnetic moment and spin of the neutron are opposite and those of the proton have the same direction). During the period of time of the order of 2•10¹⁵ years so many protons and electrons are accumulated in the stellar shell that their common magnetic field starts compensating the magnetic field from the shell’s neutrons and from rotation of the shell’s excess negative charge. Here the main role is played not by the magnetic fields from rotation of charges of the emerging protons and electrons during their rotation together with the star, because these charges are opposite in sign and create oppositely directed magnetic fields, but by the proper magnetic fields of the protons. The magnetic field of a proton is 1.46 times greater than the magnetic field of a neutron.

Therefore, at some point of time the internal magnetic field, directed at the center of the star along the rotation axis toward the spin of the star (as it is shown in the Figure), has a possibility to break out near the poles and to reverse gradually the magnetization of the stellar matter. The magnetic field is transformed into the configuration of the dipole magnetic field of a magnetar with a sharp increase in the total magnetic pressure. Part of the magnetic energy is converted into the energy, which expels the stellar shell together with the excess negative electric charge. The estimate of the magnetic energy reserve of the star is about 10⁴¹ J. ^[4] This energy would be enough to transform into plasma the matter with the mass of 0.8 Jupiter mass and corresponding, from the point of view of similarity, to the electron.

We can judge about the role of the magnetic field of the magnetar by the fact that in several hundred seconds a significant proportion of the kinetic energy of initially rapid rotation of the magnetar can be converted into the energy of jets. ^[6] Detachment of matter from the neutron star must be accompanied by $\beta ^{-}$ -decay of the excess neutrons and capture of electrons by protons, and hence by emission of electron antineutrinos and neutrinos. Therefore, the stellar electron antineutrino $~{\bar {\nu }}_{es}$ consists of ordinary electron antineutrinos $~{\bar {\nu }}_{e}$ and neutrinos $~\nu _{e}$ , emitted mainly from the stellar shell and the detached matter:

$~{\bar {\nu }}_{es}=\left\{\sum {{\bar {\nu }}_{e}}+\sum {\nu _{e}}\right\}.\qquad \qquad (1)$

Because of the strong magnetic field of the star the plasma cannot just fly away from the star, so it moves along the magnetic lines between the magnetic poles. At the same time, due to the magnetic field rotation near the star the electric field emerges, which influences the motion of matter. From the magnetic poles the charged plasma can move away from the star for large distances. Judging by the emission lifetime of stellar antineutrinos equal to $~\tau _{s}>0.05$ s, the stage of the matter ejection should occur very quickly. Probably, the same characteristic time should be expected for the gamma-ray bursts, which is often observed in magnetars. During the matter ejection from the surface of the star the excess neutrons in the atomic nuclei of ions and free neutrons decay, and other reactions of weak interaction take place. The whole set of all the emitted electron antineutrinos and neutrinos forms a stellar antineutrino. The magnetic field of the star aligns the ejected matter, and the fluxes of neutrinos and antineutrinos are also aligned.

During $\beta ^{-}$ -decay of neutrons the emerging electrons are greatly polarized and have mainly left-handed helicity. Similarly, during transformation of a neutron star into a magnetar the ejected matter must fly from the star in the direction opposite to the spin of the star. This means that the fluxes of electron antineutrinos $~{\bar {\nu }}_{e}$ from decays of neutrons in the stellar shell fly in the direction of the star’s spin and opposite to the fluxes of electrons from these decays and to the matter ejected from the star. In the weak interaction reactions with protons electron neutrinos emerge, which are emitted in the direction opposite to the spin and magnetic moment of the protons. Since the protons in the stellar shell are also oriented by the magnetic field of the star, as well as the neutrons, then the electron neutrinos from protons fly in the same direction as the electron antineutrinos from decays of neutrons. In relation (1) the sums of the fluxes of neutrinos and antineutrinos are enclosed in curved brackets, which means that these particles fly in the direction of the star’s spin and eventually the fluxes obtain right-handed helicity.

Just as in $\beta ^{-}$ -decay of neutron the electron and antineutrino $~{\bar {\nu }}_{e}$ have the opposite momenta, so in transformation of a neutron star into a magnetar the momenta of the stellar antineutrino $~{\bar {\nu }}_{es}$ and of the ejected negatively charged matter, the electron’s analogue, are also opposite.

In the present model, the neutron contains practically the same matter as the proton. The difference of the neutron is in particular configuration of the magnetic field and in the presence of a radial gradient of the electric charge. During the weak interaction reactions in the neutron’s matter a change in the magnetic field configuration takes place, the released energy ejects part of the matter from the neutron’s shell together with the negative surface charge. The neutron turns into a proton and the ejected matter turns into an electron. All this is accompanied by the emission of electron antineutrino, which turns out to be the sum of emissions from the neutron’s matter particles, decaying in weak interaction reactions.

Based on these ideas other weak interaction reactions are considered, such as reactions with pions, muons and neutrinos. ^[4] In particular, the situation with electron capture and transformation of a proton into a neutron with emission of neutrino, as well as the reaction of a proton transformation into a neutron under the action of neutrino with emission of a positron, are considered in the substantial proton model. On this basis it is concluded that the weak interaction of elementary particles is a consequence of similar interactions in the matter that occur at a deeper scale level of matter. In this case, the weak interaction is not some kind of fundamental force, but is a way of long-time transformation of the matter of elementary particles. Accordingly, the vector gauge and massive W and Z bosons, introduced in the standard theory in order to describe the weak interaction, are assumed to be not real particles but quasiparticles.

Origin

In contrast to the Big bang, in which nucleons and other hadrons arise from quarks during the cooling of the primary quark-gluon plasma across the entire expanding Universe, in the theory of Infinite Hierarchical Nesting of Matter quarks are regarded as quark quasiparticles. These quasiparticles are convenient to use for describing the properties of hadrons, however production of elementary particles does not fit into the Big Bang concept, which is associated with a number of problems. ^[7] Instead, the idea of similarity of matter levels and SPФ symmetry are involved, so that the origin of the objects at each basic level of matter occurs by the same scenario. At the level of stars the evolution of matter naturally leads to formation of massive objects – the main sequence stars, which are later transformed into white dwarfs and neutron stars. The similar process is expected at the level of elementary particles, given that ordinary neutron stars correspond to neutrons, magnetars correspond to protons, white dwarfs correspond to nuons and muons, and the discovered magnetized disks around magnetars correspond to electrons. ^[8]

The main acting forces at the level of elementary particles are assumed to be electromagnetic forces and strong gravitation, which in the gravitational model of strong interaction are considered together with the gravitational torsion field as the basis of strong interaction. The electromagnetic and gravitational forces have fundamental nature and can be explained within the framework of the Le Sage’s theory of gravitation through the properties of electrogravitational vacuum. ^[4] ^[9] ^[10] ^[11] The strong gravitation maintains the integrity of elementary particles and ensures their interaction with each other, meanwhile in the nucleons the highest density of gravitational energy is achieved. ^[12] The masses of neutron stars lie within a narrow interval of acceptable values, and it is assumed that the neutron mass is similarly limited by the equation of the nucleon matter state and by the strong gravitational constant. As a result, the masses of nucleons in different parts of the Universe do not differ much from each other.

Just as the matter of bodies, planets and stars is composed of neutrons, protons and electrons, so these particles themselves are assumed to consist of neutral and positively charged praons and negatively charged praelectrons. This follows from the principle of nesting of matter, according to which the objects of a certain basic level of matter consist of the objects of the underlying basic level of matter. Praelectrons are similar by their properties to electrons, and neutral praons are the analogues of neutrons.

From the physical and philosophical point of view, the substance, which is the essence of our world existing relatively independently, is made up of praons as the basic building blocks of elementary particles and matter particles consisting of them. In turn, praons must consist of graons as the particles of a lower basic level of matter. ^[9] In view of the above-mentioned, the title The Substantial Model of Neutron indicates that this model describes the essential substance, which gives rise to the neutron’s structure and properties.

References

1. Hofstadter R // Ann. Rev. Nucl. Sci., Vol. 7, p. 231 (1957).

2. Мостовой Ю.А., Мухин К.Н., Патаракин О.О. Нейтрон вчера, сегодня, завтра, УФН, 1996, Т. 166, С. 987-1022.

3. Александров Ю.А. О знаке и величине среднего квадрата внутреннего зарядового радиуса нейтрона, Физика элементарных частиц и атомного ядра, 1999, Т. 30, Вып.1, С. 72 – 122.

4. ^4.0 ^4.1 ^4.2 ^4.3 ^4.4 Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9.

5. Fedosin S.G. Generation of magnetic fields in cosmic objects: electrokinetic model. Advances in Physics Theories and Applications, Vol. 44, pp. 123-138 (2015). http://dx.doi.org/10.5281/zenodo.888921.

6. Vink Jacco. Supernova remnants with magnetars: clues to magnetar formation. – arXiv: astro-ph / 0706.3179, 2007.

7. Федосин С.Г. Проблемы фундаментальной физики и возможные пути их решения // Сознание и физическая реальность, Т. 9, No. 2, 2004, С. 34 - 42.

8. Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1.

9. Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.

10. Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.

11. Fedosin S.G. The Force Vacuum Field as an Alternative to the Ether and Quantum Vacuum. WSEAS Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN: 1991-8747 / 2224-3429, Volume 10, Art. #3, pp. 31-38 (2015). http://dx.doi.org/10.5281/zenodo.888979.

12. Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).

External links

· Substantial neutron model in Russian

На русском языке