На русском языке

Strong gravitational constant

Strong (nuclear) gravitation

In Astronomy the only one available characteristic empirical physical constant is the gravitational constant. Without completing the charge-mass unification or final unification: one cannot say, whether it is an ‘input to the unification’ or ‘output of unification’. The same idea can be applied to the atomic physical constants also. Sitting in a grand unified roof one cannot make an ‘absolute measurement’ but can make an ‘absolute finding’. Up till now, no atomic model has implemented the gravitational constant in the atomic or nuclear physics. Then, whatever may be its magnitude, measuring its value from existing atomic principles is impossible. Its value has been measured in the lab only within a range of 1 cm to a few metres, whereas the observed nuclear size is 1.2 fermi. Until one measures the value of the gravitational constant in microscopic physics, the debate of strong (nuclear) gravitation can be considered positively. The idea of strong gravitation originally referred specifically to mathematical approach of Abdus Salam of unification of gravitation and quantum chromodynamics, but is now often used for any particle level gravitation approach. Now many persons are working on this subject. The main advantage of this subject is: it couples black hole physics and particle physics.

Strong gravitational constant

The strong gravitational constant, denoted $~\;\; \Gamma$ or , is a grand unified physical constant of strong gravitation, involved in the calculation of the gravitational attraction at the level of elementary particles and atoms.

According to Newton's law of universal gravitation, the force of gravitational attraction between two massive points with masses and , located at a distance between them, is:

$F=G \frac{m_1 m_2}{R^2}.$

The coefficient of proportionality in this expression is called gravitational constant. It is assumed, that in contrast to the usual force of gravity, at the level of elementary particles acts strong gravitation. In order to describe it in the formula for gravitational force must be replaced on $~ \Gamma$ :

$F_{sg}=\Gamma \frac{m_1 m_2}{R^2}.$

1 Strong (nuclear) gravitation
2 Strong gravitational constant
3 Dimensions and magnitude
4 Role of squared Avogadro number
5 Connection with usual gravitational constant
6 Connection with mass and unification of interaction
7 Notes
8 See also
9 External links

Dimensions and magnitude

The dimensions assigned to the strong gravitational constant may be found from the equation above — length cubed, divided by mass and by time squared (in SI units, metres cubed per kilogram per second squared).

There are several ways to assess the value of $~ \Gamma$ . J. Dufour, under the assumption that the strong gravitational constant depends on the type of objects, from the interaction of two deuterium nuclei determined, ^[1] that $G^{'} = 2.06 \times 10^{25} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

Based on the analogy between hadrons and Kerr-Newman black holes ^[2] Sivaram, C. and Sinha, K.P, ^[3] ^[4] and Raut, Usha and Shina, KP ^[5] accepted value $\Gamma = 6.7 \times 10^{27} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

This value of the strong gravitational constant allowed estimating the strong spin-torsion interaction between spinning protons. ^[6^]

In paper of Mongan ^[7] strong gravitational constant is $G_s = 1.1 \times 10^{28} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

According to Robert Oldershaw ^[8] value of the strong gravitational constant is $G_s = 2.18 \times 10^{28} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

As in Oldershaw’ paper, strong gravitational constant could be related ^[9] with the proton radius , the proton mass and the speed of light :

$sG_p= \frac{R_p c^2}{2 m_p }= 2.4 \times 10^{28} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

According to Tennakone who identified the electron and the proton as black holes in the strong gravitational field, strong gravitational constant is: ^[10]

$\Gamma = 3.9 \times 10^{28} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

Zane Andrea Quintili finds a strong gravitational constant based on the similarity between the Planck mass and radius, and accordingly the mass and radius of the proton: ^[11]

$G_{q}={\frac {8\hbar c}{m_{p}^{2}}}=9.04\times 10^{{28}}\ {\mbox{m}}^{3}\ {\mbox{kg}}^{{-1}}\ {\mbox{s}}^{{-2}}$ .

Recami et al ^[1²^] ^[1³^] define strong gravitational constant through the mass of the pion $~ m_{\pi}$ as follows:

$N\approx \frac{h c}{ m^2_{\pi} }= 3.2 \times 10^{30} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ ,

where – Planck constant.

From this they derive constant of strong interaction of two nucleons in the following form:^[1⁴^]

$\frac{ N g^2}{\hbar c } \approx 14$ , where indicates a strong charge, $~ \hbar$ is reduced Planck constant.

Stanislav Fisenko et all found ^[1⁵^] ^[1⁶^] a spectrum of steady states of the electron in proper gravitational field (0.511 MeV …0.681 MeV) on the base of strong coupling constant

$N= 5.1 \times 10^{31} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

U. V. S. Seshavatharam and S. Lakshminarayana ^[1⁷^] in determining repelled from the Fermi constant, which led them to the value $G_s = 6.94 \times 10^{31} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

In the paper ^[1⁸^] strong gravitational constant equal to $\Gamma =2.77 \times 10^{32} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ .

Sergey Fedosin entered the strong gravitational constant in 1999 on the basis of equality between the Coulomb electric force and gravitational force in the hydrogen atom on the Bohr radius. This leads to the following expression for the value of the strong gravitational constant: ^[1⁹^]

$\Gamma= \frac{e^2}{4 \pi \varepsilon_{0} m_p m_e }=1.514 \times 10^{29} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ ,

where – elementary charge, $~ \pi$ – pi, $~ \varepsilon_{0}$ – electric constant, – the mass of proton, – the mass of electron.

It is assumed that strong gravitation, as a universal force, acts on the matter of nucleons, hadrons, electrons and elementary particles, regardless of the type of these particles. In contrast, the standard approach considers that strong interaction does not affect electrons and other leptons.

The small mass and large charge of matter do not allow the electron to be entirely in some small volume near the nucleus, and it gets disklike axisymmetric shape, which is limited by size of atom. In the hydrogen atom electrical forces between the nucleus and matter of the electron are attractive, but they are compensated by the repulsion of the intrinsic charge of the electron. There are the centripetal force of rotation of the electron around the nucleus, and the gravitational attraction between massive nucleus and matter of the electron. All these forces are equal in magnitude. From here follows that the action of strong gravitation between the masses of nucleus and electron on the one hand, and the electric force between charges of the nucleus and the electron, on the other hand, allows to estimate the value of $~ \Gamma$ . If $~R_{B}={\frac {\hbar }{m_{e}\alpha c}}$ is the Bohr radius, then the equality of forces gives:

${\frac {\Gamma m_{p}m_{e}}{R_{B}^{2}}}={\frac {e^{2}}{4\pi \varepsilon _{{0}}R_{B}^{2}}}.$

Fine structure constant is

$\alpha ={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}},$

So that

$\Gamma ={\frac {\alpha \hbar c}{m_{p}m_{e}}},\qquad \qquad \hbar ={\frac {\Gamma m_{p}m_{e}}{\alpha c}}.$

Bohr radius becomes equal

$~R_{B}={\frac {\Gamma m_{p}}{\alpha ^{2}c^{2}}}={\frac {\Gamma m_{p}}{V_{B}^{2}}},$

where $~V_{B}=\alpha c$ is the orbital speed of the electron cloud at the first energy level.

Hence $~V_{B}^{2}={\frac {\Gamma m_{p}}{R_{B}}}$ , and the kinetic energy of the electron, taking into account determination of strong gravitational constant, is equal to:

$~K={\frac {m_{e}V_{B}^{2}}{2}}={\frac {\Gamma m_{p}m_{e}}{2R_{B}}}={\frac {e^{2}}{8\pi \varepsilon _{0}R_{B}}}=-{\frac {W}{2}},$

where is the potential energy of electron in the electric field of the nucleus of a hydrogen atom.

It turns out the virial theorem in the form $~K=-{\frac {W}{2}}$ . The total electron energy is also found at the first energy level:

$~E=K+W={\frac {W}{2}}=-K=-13.6$ eV.

With the help of the constant $~ \Gamma$ the rest energy of proton in the form of a ball is equal to half of its potential energy of strong gravitational field in accordance with virial theorem, ^[²⁰^] if we assume that the binding energy $~E_{b}$ for the proton up to a sign is equal to the total energy of proton, and $~E_{b}$ becomes very close to relativistic energy in the form of rest energy:

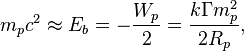
$~m_{p}c^{2}\approx E_{b}=-{\frac {W_{p}}{2}}={\frac {k\Gamma m_{p}^{2}}{2R_{p}}},$

where $~ R_p =8.73 \times 10^{-16}$ m is the proton radius, (in the hypothetical case of a uniform mass density of the proton there must be ). This implies that the mass of nucleons is determined by the energy of the strong gravitation according to the principle of mass–energy equivalence.

If we assume that the magnetic moment of the proton is created by the maximum rotation of its positive charge distributed over the volume of the proton in the form of a ball, when the centripetal acceleration at the equator becomes equal to acceleration of strong gravitation, the formula for the magnetic moment is as follows:

$~ P_m = \delta e \sqrt {\Gamma m_p R_p},$

where $~ P_m = 1.41 \times 10^{-26}$ J / T is the magnetic moment of the proton, $~ \delta = 0.1875$ (in the case of uniform density and charge should be $~ \delta = 0.2$ ).

From the formulas for the energy and the magnetic moment the radius of the proton is determined in the self-consistent model. ^[2¹^]

The strong gravitational constant is also included in the formula describing the nuclear force through strong gravitation and gravitational torsion field of rotating particles. ^[2²^] A feature of the gravitational induction is that if two bodies rotate along one axis and come close by the force of gravitation, then these bodies will increase the angular velocity of its rotation. In this regard, it is assumed that the nucleons in atomic nuclei rotate at maximum speed. This may explain the equilibrium of the nucleons in atomic nuclei as a balance between the attractive force of strong gravitation and the strong force of the torsion field (of gravitomagnetic forces in gravitoelectromagnetism). In particular, the coupling constant is

$\alpha_{pp}= \frac{\beta \Gamma m^2_p }{\hbar c }=13.4 \beta$ ,

where $~ \beta$ is equal to 0.26 for the interaction of two nucleons, and tending to 1 for bodies with a lower mass density.

The constant $~\alpha_{pp}$ is close to coupling constant of strong interaction of two nucleons in Standard Model

$\alpha_s= \frac{ g^2_{N \pi}}{4\pi\hbar c } \approx 14.6$ , where $~g_{N \pi}$ is the constant of the pseudoscalar nucleon-pionic interaction.

Fine structure constant is coupling constant of electromagnetic interaction and may be written so:

$~ \alpha = \frac { \Gamma m_p m_e }{\hbar c }\approx \frac {1}{137.036}.$

Role of squared Avogadro number

Considering Avogadro number as a scaling factor, U. V. S. Seshavatharam and S. Lakshminarayana finally arrived at a value of ^[23] ^[24] ^[25] $G_{s}=N^{2}G=2.42\times 10^{{37}}\ {\mbox{m}}^{3}\ {\mbox{kg}}^{{-1}}\ {\mbox{s}}^{{-2}}$ . It is noticed that in Hydrogen atom, ratio of total energy of electron and nuclear potential is equal to the electromagnetic and gravitational force ratio of electron where the operating gravitational constant is nothing but the atomic gravitational having a value N²G. This is a direct confirmation of the existence of the atomic or nuclear gravitational constant in nuclear physics. Therefore, this subject can now be considered as part of the mainstream research in quantum gravity.

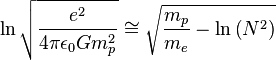The central idea is: for mole number of particles, strength of gravity is and force required to bind particles is ${\frac {c^{4}}{N.G}}.$ Force required to bind one particle is ${\frac {c^{4}}{N^{2}.G}}.$ By considering this force magnitude as the characteristic weak force magnitude, it is observed that, $\ln {\sqrt {{\frac {e^{2}}{4\pi \epsilon _{0}Gm_{p}^{2}}}}}\cong {\sqrt {{\frac {m_{p}}{m_{e}}}-\ln \left(N^{2}\right)}}$ where $m_{p}$ is the rest mass of proton and $m_{e}$ is the rest mass of electron. Obtained value of $G\cong \;6.{{\rm {6}}}66270{{\rm {1}}}79\times {{\rm {1}}}0^{{-{{\rm {1}}}1}}{{\rm {\;m}}}^{{{{\rm {3}}}}}{{\rm {Kg}}}^{{{{\rm {-1}}}}}{{\rm {sec}}}^{{{{\rm {-2}}}.}}$ Here the most important point to be emphasized is ${\frac {c^{4}}{G}}$ can be considered as the classical or upper limit of gravitational or electromagnetic force. It can be considered as the grand unified force. It is the origin of Planck scale and of the black hole astrophysics.

Connection with usual gravitational constant

With the help of similarity of matter levels and SPФ symmetry in Theory of Infinite Hierarchical Nesting of Matter the value of $~ \Gamma$ can also be defined in terms of coefficients of similarity and gravitational constant:

$\Gamma = G \frac{ \Phi }{ P S^2},$

where $\Phi =1.62 \times 10^{57}$ , $P= 1.4 \times 10^{19}$ , are the coefficients of similarity in mass, size and speed, respectively, for the degenerate quantum objects at the atomic and stellar levels of matter.^[19] The powers of similarity coefficients in this equation correspond to the dimension of gravitational constant according to dimensional analysis.

From the standpoint of Infinite Hierarchical Nesting of Matter and Le Sage's theory of gravitation, the presence of two gravitational constant $~ \Gamma$ and shows the difference between the properties of gravitons and properties of matter at different levels of matter. ^[2⁶^{] [2}⁷^]

In particular, for the strong gravitational constant and the ordinary gravitational constant it is possible to write similar relations, in which these constants are expressed in terms of the corresponding energy densities of gravitons’ fluxes in electrogravitational vacuum and the parameters of the densest object of the corresponding level of matter: ^[^28]

$~\Gamma ={\frac {\varepsilon _{c}\vartheta ^{2}}{4\pi M_{n}^{2}}},\qquad \qquad G={\frac {\varepsilon _{{cs}}\vartheta _{s}^{2}}{4\pi M_{s}^{2}}},$

where $~\varepsilon _{c}=7.4\cdot 10^{{35}}$ J/m³ is the energy density of the graviton fluxes for cubic distribution; $~\vartheta =2.67\cdot 10^{{-30}}$ m² is the cross-section of interaction of the charged particles of the electrogravitational vacuum (praons) with nucleons, which is very close in magnitude to the geometrical cross-section of the nucleon and is used to calculate the electric constant; $~M_{n}$ is the mass of the nucleon; $\varepsilon _{{cs}}=\varepsilon _{c}{\frac {\Phi S^{2}}{P^{3}}}=2.3\cdot 10^{{34}}$ J/m³ is the energy density of the graviton fluxes at the stellar level for cubic distribution; $~\vartheta _{s}=\vartheta P^{2}=5.2\cdot 10^{{8}}$ m² is the cross-section of interaction between the gravitons and a neutron star; $~M_{s}=M_{n}\Phi =2.7\cdot 10^{{30}}$ kg is the mass of the neutron star.

At the matter level of praons, its own strong gravitational constant $~G_{{pr}}$ must act. Considering that the coefficient of similarity in speed between the nucleon and praon levels of matter is $~S\approx 1$ , we can write:

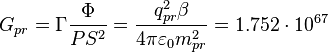$G_{{pr}}=\Gamma {\frac {\Phi }{PS^{2}}}={\frac {q_{{pr}}^{2}\beta }{4\pi \varepsilon _{{0}}m_{{pr}}^{2}}}=1.752\cdot 10^{{67}}$ m³•s^–2•kg^–1,

where $~q_{{pr}}=1.06\cdot 10^{{-57}}$ C is the charge of the praon, $~m_{{pr}}=1\cdot 10^{{-84}}$ kg is the mass of the praon, $~\beta ={\frac {m_{p}}{m_{e}}}=1836.152$ is the proton to electron mass ratio.

Connection with mass and unification of interaction

The main object of unification is to understand the origin of elementary particles mass, (Dirac) magnetic moments and their forces. Right now and till today ‘string theory’ with 4 + 6 extra dimensions not in a position to explain the unification of gravitational and non-gravitational forces. More clearly speaking it is not in a position to bring down the planck scale to the nuclear size. Physicists say – if strength of strong interaction is unity, with reference to the strong interaction, strength of gravitation is 10⁻³⁹. The fundamental question to be answered is: is mass an inherent property of any elementary particle?

One can say: for any elementary particle mass is an induced property. This idea makes grand unification easy. Note that general relativity does not throw any light on the ‘mass generation’ of charged particles. It only suggests that space-time is curved near the massive celestial objects. More over it couples the cosmic (dust) matter with geometry. But how matter is created? Why and how elementary particle possesses both charge and mass? Such types of questions are not discussed in the frame work of general relativity.

The first step in unification is to understand the origin of the rest mass of a charged elementary particle. Second step is to understand the combined effects of its electromagnetic (or charged) and gravitational interactions. Third step is to understand its behavior with surroundings when it is created. Fourth step is to understand its behavior with cosmic space-time or other particles. Right from its birth to death, in all these steps the underlying fact is that whether it is a strongly interacting particle or weakly interacting particle, it is having some rest mass. To understand the first two steps somehow one can implement the gravitational constant in sub atomic physics.

To bring down the Planck mass scale to the observed elementary particles mass scale a large scale factor is required. Just like relative permeability and relative permittivity by any suitable reason in atomic space if one is able to increase the value of classical gravitational constant, it helps in four ways. Observed elementary particles mass can be generated and grand unification can be achieved. Third important application is characteristic building block of the cosmological dark matter can be quantified in terms of fundamental physical constants. Fourth important application is – no extra dimensions are required. Finally nuclear physics and quantum mechanics can be studied in the view of strong nuclear gravity where nuclear charge and atomic gravitational constant play a crucial role in the nuclear space-time curvature, quantum chromodynamics and quark confinement. Not only that cosmology and particle physics can be studied in a unified way. In this connection it is suggested that square root of ratio of atomic gravitational constant and classical gravitational constant is equal to the Avogadro number. ^[2⁹^] The Avogadro constant expresses the number of elementary entities per mole of substance and it has the value mol^–1. Avogadro's constant is a scaling factor between macroscopic and microscopic (atomic scale) observations of nature. It is an observed fact. The very unfortunate thing is that even though it is a large number it is neither implemented in cosmology nor implemented in grand unification.

Here the very important question to be answered is – which is more fundamental either $G$ or $G s$ ? It is proposed that both can be considered as the 'head' and 'tail' of matter coin. It can also be suggested that classical $G$ is a consequence of the existence of atomic $G s$ . It is known that there is a difference in between 'absolute findings' and 'absolute measurements'. Absolute findings can be understood where as 'absolute measurements' can not be made by nuclear experiments which are being conducted under the sky of universal gravity with unknown origin of elementary particles mass.

Till today there is no explanation for this fantastic and large difference between $G$ or $G s$ or between gravitation and strong interaction, about 10⁻³⁹. It can be supposed that elementary particles construction is much more fundamental than the black hole's construction. If one wishes to unify electroweak, strong and gravitational interactions it is a must to implement the classical gravitational constant $G$ in the sub atomic physics. ^[30] By any reason if one implements the Planck scale in elementary particle physics and nuclear physics automatically $G$ comes into subatomic physics. Then a large arbitrary number has to be considered as a proportionality constant. After that its physical significance has to be analyzed. Alternatively its equivalent 'strong atomic gravitational constant' can also be assumed. Some attempts have been done in physics history.

Whether it may be real or an equivalent if it is existing as a 'single constant' its physical significance can be understood. Nuclear size can be fitted with 'nuclear Schwarzschild radius'. Nucleus can be considered as 'strong nuclear black hole'. This idea requires a basic nuclear fermion! Nuclear binding energy constants can be generated directly. Proton-neutron stability can be studied. Origin of strong coupling constant and Fermi's weak coupling constant can be understood. Charged lepton masses can be fitted. Such applications can be considered favorable for the proposed assumptions and further analysis can be carried out positively for understanding and developing this proposed 'Avogadro's strong nuclear gravity'.

Unification means: finding the similarities, finding the limiting physical constants, finding the key numbers, coupling the key physical constants, coupling the key physical concepts, coupling the key physical properties, minimizing the number of dimensions, minimizing the number of inputs and implementing the key physical constant or key number in different branches of physics. This is a very lengthy process. In all these cases observations, interpretations, experiments and imagination play a key role. The main difficulty is with interpretations and observations. As the interpretation changes physical concept changes, physical equation changes and finally the destiny changes.

Note that human beings are part of this universal gravity. There are some natural restrictions to experiments. Seeing a black hole is highly speculative. But indirectly its significances can be well understood. In the similar way in nuclear and particle physics: any experimental setup which is being run under the influence of the proposed strong nuclear gravity, without knowing the probing particle’s massive origin, without knowing the massive origin of the nucleus: based on ‘grand unified scheme’ one may not be able to unearth the absolute findings. Note that observer, experimental setup and the probing particle all are under the same influence of universal gravity. When searching for an experimental proof in grand/final unification scheme or dark matter projects this fact may be considered positively for further analysis.

To conclude it can be suggested that – existence of strong gravitational constant as Atomic gravitational constant is true and its consequences can be understood easily and can be implemented easily in grand unification program and dark matter projects.

Notes

J. Dufour. "Very sizeable increase of gravity at pico-meter distance: a novel working hypothesis to explain anomalous heat effects and apparent transmutations in certain metal hydrogen systems". J. of condensed matter nuclear science, Vol. 1, pp. 47-61 (2007).
Strong Interactions, Gravitation and Cosmology. Abdus Salam Publ. in: NATO Advanced Study Institute, Erice, June16-July 6, 1972 ; in: High Energy Astrophysics and its Relation to Elementary Particle Physics, 441-452 MIT Press, Cambridge (1974).
Sivaram, C. and Sinha, K.P. Strong gravity, black holes, and hadrons. Physical Review D, Vol. 16, Issue 6, pp. 1975-1978 (1977).
Salam A. and Sivaram C. Strong Gravity Approach to QCD and Confinement. Mod. Phys. Lett., v. A8(4), pp. 321-326 (1993).
Raut, Usha and Shina, KP (1983) Strong gravity and the fine structure constant. In: Proceedings of the Indian Academy of Sciences Part A: Physical Sciences, 49 (2). pp. 352-358.
V. de Sabbata, C. Sivaram. Strong Spin-Torsion Interaction between Spinning Protons. Il Nuovo Cimento, Vol. 101A, N. 2, pp. 273-283 (1989).
T. R. Mongan. Cold dark matter from "strong gravity". General Relativity & Quantum Cosmology, 20 Jun 2007; arXiv:0706.3050v2.
Oldershaw R.L. Discrete Scale Relativity. Astrophysics and Space Science, Vol. 311, N. 4, pp. 431-433 (2007). http://dx.doi.org/10.1007/s10509-007-9557-x.
Stone R.A. Quark Confinement and Force Unification. Progress in Physics, Vol. 2, pp. 19-20 (2010).
K. Tennakone. Electron, muon, proton, and strong gravity. Phys. Rev. D, Volume 10, Issue 6, pp.1722-1725 (1974).
Zane Andrea Quintili. Gravitational Field and Proton Radius. vixra.org. (2019).
Recami, E.; Ammiraju, P.; Hernandez, H.E.; Kretly, L.C.; Rodrigues, W.A., Jr. Elementary particles as micro-universes: a geometric approach to "strong gravity". Apeiron, January 01, 1997.
Recami E. and Tonin-Zanchin V. The strong coupling constant: its theoretical derivation from a geometric approach to hadron structure. Found. Phys. Lett., v, 7(1), pp. 85-92 (1994).
Erasmo Recami, Tonin-Zanchin, Antonino Del Popolo, Mario Gambera. The strong coupling constant, Heavy Ion Physics, Vol. 10, pp. 345-349 (1999).
Stanislav Fisenko & Igor Fisenko. The Conception of Thermonuclear Reactor on the Principle of Gravitational Confinement of Dense High-temperature Plasma. Applied Physics Research, Vol. 2, No. 2, pp. 71-79 (2010).
S. I. Fisenko, M. M. Beilinson and B. G. Umanov. Some notes on the concept of “strong” gravitation and possibilities of its experimental investigation. Physics Letters A, Volume 148, Issues 8-9, pp. 405-407 (1990).
U. V. S. Seshavatharam and S. Lakshminarayana. Strong nuclear gravitational constant and the origin of nuclear planck scale. Progress in Physics, vol. 3, pp. 31-38 (2010). [1]
Perng J. J. Strong gravitation and elementary particles. Nuovo Cimento, Lettere, Serie 2, vol. 23, N. 15, pp. 552-554 (1978).
^18.0 ^18.1 Fedosin S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik, Perm, (1999-06-09) 544 pp. ISBN 5-8131-0012-1.
Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9.
Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012).
Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
U. V. S. Seshavatharam and S. Lakshminarayana. Unified model of universe and the atom. Book.ISBN: 9783843393966, LAP LAMBERT Academic Publishing GmbH & Co. KG, Germany, 2011 March 30.
U. V. S. Seshavatharam and S. Lakshminarayana. Role of Avogadro number in grand unification. Hadronic Journal. Vol. 33, No 5, p. 513 (2010).
U. V. S. Seshavatharam and S. Lakshminarayana. Atomic gravitational constant and the origin of elementary magnetic moments. To be published.
Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009).
Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.
AGNI – Avogadro's gravity for nuclear interactions. Nuclear experiments blog: Journal of Nuclear Physics, Nov. 2010.
Seshavatharam, U. V. S.; Lakshminarayana, S. Super symmetry in strong and weak interactions. International journal of modern physics E, Issue 02, pp. 263-280, Feb.2010.

External links

Strong gravitational constant (in Russian)

Source: http://sergf.ru/psgen.htm

On the list of pages