На русском языке

Electrogravitational vacuum

From Wikiversity

 

Electrogravitational vacuum describes properties of physical vacuum and cosmic space devoid of matter based on the modernized Le Sage’s theory of gravitation and implies that the vacuum is filled with particles called gravitons and with tiny charged particles. Some of these particles have a large Lorentz factor, similarly to ultra-high-energy cosmic rays, which imparts a dynamic character to the vacuum. Due to high penetrating capacity when moving in matter, these particles are considered to be responsible for emergence of gravitational [1] [2] [3] and electromagnetic [4] [5] forces between bodies. In addition, photons and neutrinos can consist of these particles. [6] The composition of these particles and their properties are determined using the theory of Infinite Hierarchical Nesting of Matter, similarity of matter levels and SPФ symmetry. In particular, fluxes of charged particles such as praons are assumed to be the main active component of the electrogravitational vacuum. [7]

Contents

Existing models of vacuum

In physics, there are numerous models suggested to define the vacuum characteristics. Thus, the vacuum of free space, in which the laws of classical electromagnetism hold true, should satisfy the following conditions:

In Lorentz-invariant theory of gravitation the vacuum is characterized as follows:

The above characteristics of classical vacuum are presented in the article on vacuum constants.

In General Relativity, the vacuum solution (general relativity) can be obtained when gravitational field in the absence of electromagnetic field is calculated in empty space outside matter, where the stress-energy tensor of matter and non-gravitational fields is equal to zero. Despite the equality of this tensor to zero, in empty space there still can be curvature of spacetime, which, through the metric tensor and its derivatives, defines the effect of gravitation from some local or global source. Besides, variations in solutions are possible, which depend on taking into account the cosmological constant and the choice of its sign. Due to the connection with the metric tensor, the gravitational field in this theory is a tensor field.

Its own vacuum is also assumed within covariant theory of gravitation, in which gravitational field is a vector field, since it is given by the four-potential and gravitational tensor. In this case, the connection between gravitation and geometry, between gravitational field and metric tensor, which is characteristic of general theory of relativity, is broken. The gravitational field is assumed to be physical interaction, which, just as electromagnetic interaction, becomes independent of the metric tensor that characterizes the properties of spacetime depending on parameters of source of gravitational field. The source of gravitational field here means some material object or physical system of matter and its proper fields, and the vacuum is treated as a contents of space outside the system’s matter. For infinite space that does not contain a visible source of gravitational field, it follows from the field equations that gravitational field strength {\displaystyle ~\mathbf {\Gamma } } and gravitational torsion field {\displaystyle ~\mathbf {\Omega } }  in the simplest case are constant vectors that do not depend on time. Provided that {\displaystyle ~\mathbf {\Gamma } =0}  and {\displaystyle ~\mathbf {\Omega } =0,} in such a space the scalar potential {\displaystyle ~\psi } and the vector potential {\displaystyle ~\mathbf {D} } of gravitational field should be constant values, independent of coordinates and time. Thus, it can be assumed that in the vacuum, far from the sources of gravitational field, both the four-potential and the gravitational tensor vanish. Another peculiarity of this vacuum is that, due to gauging of system’s relativistic energy and equation for the metric, outside the matter both the cosmological constant and the scalar curvature vanish. [8] Meanwhile in relativistic uniform system both the cosmological constant and scalar curvature inside matter turn out to be constant values.

In quantum physics, the basic quantity is Planck constant as a typical quantity of action for any particles under consideration. Taking this quantity into account changes vacuum properties required for the theory. Thus, in quantum electrodynamics, it is assumed that electromagnetic interaction between charged particles occurs by means of photons as carriers of interaction. This means that the charged particles must absorb and emit photons in order to change their energy and momentum. QED vacuum is assumed to be filled with various virtual particles, including short-lived photons and electron-positron pairs. Virtual particles define zero-point oscillations of the vacuum as its ground state. The energy of the vacuum’s zero-point oscillations is called zero-point energy, its exact magnitude is unknown. It is supposed that a change in zero-point energy with a change in system’s configuration in vacuum leads to Casimir effect. Under influence of electromagnetic field, vacuum polarization takes place and various subtle effects can occur. In this case, the vacuum will become diamagnetic, so that relative magnetic permeability will be less than unity. The vacuum also exhibits dielectric properties, since relative permittivity is greater than unity.

One of the problems of such vacuum is that zero-point energy, which is estimated to have a very large magnitude, does not manifest itself as a source of gravitational field and is not part of mathematical apparatus of general theory of relativity. This leads to the problem of discrepancy between the vacuum’s zero-point energy and observed small value of cosmological constant, which is known as cosmological constant problem.

The vacuum of quantum chromodynamics is considered to be filled with gluon condensate and fermionic condensate of quarks. Both condensates can give mass to elementary particles and hadrons, and fermionic condensate possesses superfluidity. The condensates should have such properties that the color confinement and hadrons’ masses could be explained.

QED vacuum and QCD vacuum are the constituent parts of vacuum in Standard Model, which, however, does not take into account gravitation.

The superfluid vacuum, containing some superfluid or Bose-Einstein condensate, is viewed as a basis for quantum-based unification of all four fundamental interactions, including weak interaction, strong interaction, electromagnetic interaction, and gravitational interaction. The fluid is assumed to consist of fermion-antifermion pairs and is described with the help of macroscopic wave function. Interaction of the fluid with elementary particles gives mass to the latter. At low energies and momenta of the fluid fluctuations, treated as virtual particles, this fluid is considered an ideal one, leading to Lorentz covariance. However, attempts to present gravitation as a consequence of relativistic motion of the fluid fluctuations did not produce a result. The probable reason for this is said to be the fact that macroscopic curvature of spacetime in general theory of relativity can be the long-wavelength limit that does not work on the small scales of quantum gravitation.

Unfortunately, all the vacuum models presented above mainly describe its properties, which are required in one or another theory. As for the substantial component of the vacuum, which defines its structure and represents the specific carriers that determine characteristics of the vacuum, the information here is either missing or extremely speculative.

Description of electrogravitational vacuum model

Composition of vacuum’s particles

The electrogravitational vacuum model is based on the theory of Infinite Hierarchical Nesting of Matter, which considers the universe from the point of view of scale dimension, SPФ symmetry, similarity of matter levels and quantization of parameters of cosmic systems. On the scale axis all objects of universe can be placed, which are grouped into matter levels. Each basic level of matter has its own most dense and long-lived objects with the maximum energy density, with strong gravitational, electric and magnetic fields. At the level of stars these objects are neutron stars, at the atomic level they are nucleons. Neutron stars consist of nucleons, and by analogy nucleons consist of praons, and praons consist of graons. Praons and graons have their own levels of matter, similar to the nucleon level of matter.

In the electrogravitational model, the vacuum includes a set of densest objects of an infinite number of those matter levels that are below the matter level corresponding to the observer. For a human observer the main components of te physical vacuum are individual nucleons, praons, graons and even smaller particles, as well as complex and composite objects that consist of them. For example, atomic nuclei consist of nucleons, and we can conceive similar nuclei of praons or graons. It is assumed that ordinary photons emitted by atoms consist of praons, and the neutrinos observed in experiments consist of graons. [6] Since masses of main objects in the chain of matter levels: neutron star-nucleon-praon-graon -... are rapidly decreasing, it is obvious that at present it is quite difficult to detect and register in the vacuum individual praons or individual photons consisting of graons.

If observer belonged to the metagalactic level of matter, then for him the vacuum would also contain such objects as neutron stars, white dwarfs, ordinary main sequence stars and planets. All these objects are composed of nucleons and have their analogues on the nucleon level of matter. Thus, the analogue of a white dwarf from the point of view of matter evolution under action of gravitation is a nuon, and from the point of view of matter’s radioactive decay the analogue of a white dwarf is a muon. The neutron star of the lowest possible mass is the analogue of a pion.

In addition to nucleons, matter also contains electrons, the analogues of which at the level of stars are discons, that is, massive discs discovered in some neutron stars and magnetars. [9] [10] Discons, just as the stars themselves, can carry an electric charge. A magnetar with a positive charge and a discon with a negative charge are analogous to a hydrogen atom in hydrogen system. Galaxies correspond to smallest dust particles, in the center of which there is solid matter and on the outside, there is thick gaseous shell of different atoms. The latter analogue becomes thicker over time, since the stars in galaxies evolve and turn into neutron stars and white dwarfs. In this picture magnetars are formed from neutron stars, just as protons are formed in free neutron decay. The matter of discons in its density and composition must be close to the density and composition of planets and must contain mainly elements like iron and other metals. Since all stars, planets and discons are composed of nucleon matter, under appropriate conditions all these objects can be transformed and generate each other.

Objects like discons and electrons must be present at every level of matter, forming together with the main objects the corresponding matter. For example, elementary particles (nucleons, electrons, hadrons and leptons) must consist of praons and praelectrons just as stars and planets consist of nucleons and electrons. This allows elementary particles to transform into each other. The similarity between the matter levels allows us to construct the models of elementary particles, such as the substantial neutron model, the substantial proton model, the substantial electron model, the substantial photon model.

We assume that black holes do not exist, as they are attributed the property of absorbing matter and do not letting anything out. But this contradicts the fact that the graviton field penetrates all bodies, and thereby creates gravitational phenomena. If a black hole would only absorb the energy of graviton fluxes, it would acquire in a short time a huge amount of mass-energy and should grow indefinitely in size, which is not observed.

The highly rarefied vacuum of cosmic space outside dust and gas clouds may contain:

By analogy, from the point of view of a human observer the electrogravitational vacuum must contain all those smallest objects that either cannot be directly registered in experiment, or are the sources generating gravitational and electromagnetic fields, and are also causing strong and weak interactions. Thus, this vacuum includes praons, graons and even smaller particles, as well as objects consisting of them, which have smaller masses and energies than the known elementary particles.

Physical parameters of vacuum particles

In order to determine parameters of vacuum particles the similarity theory is used. A typical neutron star has a mass of 1.35 solar masses, a radius of about 12 km, and characteristic speed of particles’ motion in such a star reaches the value of 0.23 the speed of light. Dividing these quantities by the corresponding quantities for the proton, we find the coefficients of similarity: in mass  Ф = 1.62∙1057 , in size  Р = 1.4∙1019 , in speed  S = 2.3∙10-1 . In the first approximation, we can assume that the same coefficients of similarity in mass and size are also valid for the relation between praons and nucleons. Hence we can determine the praon’s mass {\displaystyle ~m_{pr}=1\cdot 10^{-84}} kg and radius {\displaystyle ~r_{pr}=6.2\cdot 10^{-35}} m. Using the praon’s mass and radius, we can estimate the average density of its matter {\displaystyle ~\rho _{pr}=1\cdot 10^{18}} kg/m3 .

The characteristic speed of particles of matter inside a proton and a praon is quite close to the speed of light. If at the center of a neutron star the Lorentz factor reaches the value {\displaystyle ~\gamma _{cs}=1.04,} then at the center of a proton the Lorentz factor for the praons located there is equal to  {\displaystyle ~\gamma _{cp}=1.9.}[11]   Hence it follows that coefficient of similarity in speed for the levels of nucleons and praons is close to unity, {\displaystyle ~S\approx 1} . Taking this into account it is possible to determine the gravitational constant {\displaystyle ~G_{pr}} acting on the praon level of matter. The similarity relations between the levels of praons and nucleons give: {\displaystyle ~{\frac {G_{a}}{G_{pr}}}={\frac {PS^{2}}{\Phi }}} , and therefore {\displaystyle ~G_{pr}=1.752\cdot 10^{67}} m3•s–2•kg–1.

The Boltzmann constant for the level of praons at {\displaystyle ~S\approx 1}  is given by the expression: {\displaystyle ~k_{pr}={\frac {k}{\Phi S^{2}}}=1.6\cdot 10^{-79}} J/K , where {\displaystyle ~k}  is the Boltzmann constant.

If we calculate kinetic energy of a proton {\displaystyle ~E_{k}=(\gamma _{cs}-1)m_{p}c^{2}}  as for a certain typical particle moving at the center of a neutron star, then using the equality {\displaystyle ~E_{k}={\frac {3}{2}}kT_{s}}  we can estimate the maximum temperature at the center of the star: {\displaystyle ~T_{s}=2.8\cdot 10^{11}} K. Similarly, the temperature at the center of a proton will be {\displaystyle ~T_{p}={\frac {2(\gamma _{c}-1)m_{pr}c^{2}}{3k_{pr}}}=3.4\cdot 10^{11}} K.

The typical angular momentum at each level of matter is given by corresponding Dirac constant. For compact stars the stellar Dirac constant is {\displaystyle ~\hbar _{s}=\hbar \Phi PS=5.5\cdot 10^{41}} J∙s, for the nucleon level of matter the Dirac constant is {\displaystyle ~\hbar =1.054\cdot 10^{-34}} J∙s, while the quantum spin of a nucleon is equal to {\displaystyle ~\hbar /2} . In order to estimate the Dirac constant {\displaystyle ~\hbar _{pr}} at the level of praons, the similarity relation is applied: {\displaystyle ~{\frac {\hbar }{\hbar _{pr}}}=\Phi PS} . If the coefficient of similarity in speed is {\displaystyle ~S\approx 1} , then we obtain {\displaystyle ~\hbar _{pr}=4.6\cdot 10^{-111}} J∙s. Then from the similarity theory it follows that photons of the praon level of matter have energies {\displaystyle ~\Phi S^{2}\approx 1.62\cdot 10^{57}} less than the energies of the corresponding photons of the nucleon level of matter. Accordingly, we can say approximately the same with respect to the difference between the energies of relativistic graons, relativistic praons and high-energy cosmic rays. It is assumed that graons are responsible for strong gravitation, and praons are responsible for ordinary gravitation, while the Dirac constant for graons is substantially less than the Dirac constant {\displaystyle ~\hbar _{pr}} for praons. The picture described above differs fundamentally from the quantum gravitation approach, which considers gravitons as objects that necessarily have a spin in the form of the Dirac constant {\displaystyle ~\hbar } .

For the strong gravitational constant the following relation holds true:

{\displaystyle G_{a}={\frac {e^{2}}{4\pi \varepsilon _{0}m_{p}m_{e}}}={\frac {e^{2}\beta }{4\pi \varepsilon _{0}m_{p}^{2}}},}

where {\displaystyle ~e}  is the elementary charge, {\displaystyle ~\varepsilon _{0}}  is the electric constant, {\displaystyle ~m_{p}}  is the proton mass,

{\displaystyle ~m_{e}} is the electron mass, {\displaystyle ~\beta ={\frac {m_{p}}{m_{e}}}=1836.152}  is the ratio of the proton mass to the electron mass.

Similarly, at the level of praons we have the following:

{\displaystyle G_{pr}={\frac {q_{pr}^{2}\beta }{4\pi \varepsilon _{0}m_{pr}^{2}}}.}

Hence we find the praon charge {\displaystyle ~q_{pr}=1.06\cdot 10^{-57}} C.

Acting similarly, we can obtain the parameters of graons and other vacuum particles.

Gravitational field

In the model under consideration, the gravitation effect arises under action of gravitons – the smallest relativistic vacuum particles that fill the whole space and act within the framework of modernized Le Sage’s theory. Besides, each basic level of matter is characterized by its own gravitational constant. For the level of stars it is the ordinary gravitational constant, and for the nucleon level of matter it is the strong gravitational constant. [12] The particles of the graon level of matter are assumed to be responsible for the effect of strong gravitation, which holds nucleons and elementary particles in integrity, and the particles of the praon level of matter are responsible for the ordinary gravitation.

The gravitons can be both neutral particles, such as neutrinos and photons, and relativistic charged particles, similar in their properties to cosmic rays. The effective mass of all these particles is their relativistic mass-energy, taking into account the great in magnitude Lorentz factor. In particular, the gravitons can be the praons accelerated by the strong fields near nucleons almost to the speed of light. As part of the graviton field, such relativistic praons can participate in creation of ordinary gravitation, according to the Le Sage’s model, and give mass to the bodies at the macrolevel. In this case, the praons have their own rest mass, which arises from the action of the gravitons of lower levels of matter. During interaction with the fields and matter, relativistic praons can produce high-energy photons, which can also serve as the particles of the graviton field. The energy of ordinary photons is proportional to their frequency and the Planck constant. But for the particles belonging to different levels of matter, the value of the Planck constant varies considerably according to the infinite nesting of matter – the lower is the level of matter, the less is respective Planck constant and the lower is the energy of photons at this level of energy. As a result, the graviton field represents a multi-component system of particles, photons and neutrinos, the energies of which are associated with each of an infinite number of matter levels.

The energy density of graviton fluxes responsible for gravitation in the model of cubic distribution of fluxes of particles in space equals: [2] [5]

{\displaystyle ~\varepsilon _{c}={\frac {4\pi Gm_{p}^{2}}{\sigma ^{2}}}={\frac {4\pi G_{a}m_{p}^{2}}{\vartheta ^{2}}}=7.4\cdot 10^{35}} J/m 3,

where {\displaystyle ~G}  is the gravitational constant, {\displaystyle ~m_{p}}  is the proton mass, {\displaystyle ~\sigma =5.6\cdot 10^{-50}}  m2 is the cross-section of interaction of gravitons with the matter for the ordinary gravitation,

{\displaystyle ~G_{a}=1.514\cdot 10^{29}} m3•s–2•kg–1  is the strong gravitational constant, {\displaystyle ~\vartheta =2.67\cdot 10^{-30}} m2  is the cross-section of interaction of the vacuum’s charged particles with nucleons during electromagnetic interaction. In this case, the relation holds: {\displaystyle ~\vartheta =\sigma {\frac {G_{a}}{G}}} .

The obtained value of energy density of graviton fluxes defines field mass-energy limit and exceeds the rest energy density of the proton  {\displaystyle ~{\frac {3m_{p}c^{2}}{4\pi r_{p}^{3}}}=5.4\cdot 10^{34}} J/m3 , with the proton radius {\displaystyle ~r_{p}=8.73\cdot 10^{-16}} m according to the article. [13]

The flux of gravitons’ energy in one direction has the value of the order of {\displaystyle ~3.7\cdot 10^{43}} W/m2. If gravitons represented the electromagnetic field quanta, then for the temperature of the field of gravitons in the form of photons we can get an estimate {\displaystyle ~5.6\cdot 10^{12}} K.

The expressions for gravitational field strengths inside and outside the ball, obtained in the model of gravitons, are in good agreement with the values of the field strengths in Lorentz-invariant theory of gravitation. [2] Going from field strengths to field potentials, using Lorentz transformation, introducing gravitational four-potential, one can find gravitational stress-energy tensor, gravitational field equations, gravitational force, as well as contribution of gravitational field into equation for the metric. This means that the gravitational field theory both in the flat Minkowski space and in the curved spacetime is fully proved at the substantial level through the graviton field. And dependence of metric on gravitational field potential allows us to take into account influence of inhomogeneous graviton field on results of space-time experiments, based as a rule on the use of electromagnetic waves and devices.

As for the value of limiting force of attraction between two contacting massive bodies, the following value was found: [1]

{\displaystyle ~F_{max}={\frac {c^{4}}{16k^{2}G}}\approx 2\cdot 10^{43}} N,

which implies the case when the graviton fluxes are completely retained by these bodies.

Here {\displaystyle ~c}  is the speed of light, {\displaystyle ~k=0.6}  for the case of uniform density. If we divide {\displaystyle ~F_{max}}  by the mass of a typical neutron star, which is equal to {\displaystyle ~M_{s}=1.35}  solar masses, we obtain the acceleration {\displaystyle 7.5\cdot 10^{12}} m/s2. For comparison, the gravitational acceleration on the surface of this star, with its radius {\displaystyle ~R_{s}=12} km, is equal to {\displaystyle 1.2\cdot 10^{12}} m/s2.

The difference between the Newton’s formula for the force {\displaystyle ~F_{N}} of attraction between two neutron stars in their contact and the formula that takes into account the scattering of gravitons in the stars’ matter due to high density of matter leads to reduction of acting force to the value {\displaystyle ~0.26F_{N}}. [3]

The presented model describes how bodies acquire mass as a measure of inertia. The body mass can be expressed in terms of luminosity of those graviton fluxes that interacted with the body matter and transferred their momentum to it. In this case, the graviton luminosity is proportional and almost equal to the rest energy of the body, released from the body per time of gravitons’ passing the radius of the body. The body mass at a constant volume is proportional to the concentration of nucleons, and similarly the number of interactions of gravitons with nucleons increases with increasing of concentration of nucleons. Thus, the body’s inertia as the resistance to the applied force and gravitational mass of the body are caused by the action of graviton field on the given body. As it follows from the principle of relativity, at a constant velocity the action of graviton fluxes from different sides is balanced, but it is not so in case of the body’s acceleration. When the body is accelerated, a force must be applied and work must be carried out to bring the body from the state with one velocity into the state with a different velocity. This work is done against the action of gravitons fluxes and leads to the concept of mass as a measure of the body’s inertia proportional to applied force and inversely proportional to the emerging acceleration.

The gravitational mass is determined from the expressions for gravitational field’s strength and potential, and therefore it differs from the inertial mass of the body, since the latter takes into account contributions to the mass from all the body’s proper fields. In relativistic uniform system, it is found that the inertial mass is less than the gravitational mass, {\displaystyle ~M<m_{g}.}[14] [15]

As a rule, the majority of gravitons pass through matter without losing their energy and momentum. An estimate of total graviton luminosity of a neutron star as the power of energy fluxes of gravitons passing through the star and interacting with its matter yields a value of the order of {\displaystyle ~2\cdot 10^{52}} W. If we divide this value by the number of nucleons in the neutron star, we obtain the average luminosity of those gravitons that interact with each nucleon of matter and transfer their momentum to it: [2]

{\displaystyle ~P_{1}=\varepsilon _{c}\sigma c=1.2\cdot 10^{-5}} W.

The meaning of this value at first glance is not quite clear. However, with the help of similarity coefficients we can calculate a similar value at the level of stars – the luminosity of those gravitons that interact with each neutron star and impart mass to it due to the loss of their momentum:

{\displaystyle ~P_{1s}=P_{1}{\frac {\Phi S^{3}}{P}}=1.7\cdot 10^{31}} W.

In physics, there is such a known quantity as Eddington luminosity, which means the limiting luminosity of a star. When this luminosity is exceeded, the star begins to lose mass due to ejection of matter from the surface under action of radiation from the star. If a neutron star with the mass {\displaystyle ~M_{s}=1.35M_{c}} , where {\displaystyle ~M_{c}}  is the mass of the Sun, has ionized hydrogen in its atmosphere, then the Eddington luminosity for it would be equal to {\displaystyle ~L_{Edd}=1.26\cdot 10^{31}\left({\frac {M_{s}}{M_{c}}}\right)=1.7\cdot 10^{31}} W.

The coincidence of the quantities {\displaystyle ~P_{1s}}  and {\displaystyle ~L_{Edd}}  seems surprising, but it is not accidental, since both quantities have limiting character and are associated with the integrity of the neutron star as such. Due to {\displaystyle ~P_{1s}}  the star does not only gain mass as a measure of inertia in graviton fluxes, but also acquires quite definite distribution of pressure and temperature in matter, reaching a maximum at the center. Solving the equations of acceleration field allows us to calculate dependence of Lorentz factor of the particles’ motion inside the star as a function of current radius. [16] The star cannot cool down below the limit, which is set by the graviton fluxes for each state of matter, and therefore it always has a certain minimum degree of heating of this matter, the corresponding binding energy, potential gravitational energy and gravitational acceleration. Under action of gravitational acceleration, the nucleons are forced against the surface of the star, but if the star has radiation luminosity {\displaystyle ~L_{Edd}} , which is equal to the luminosity of gravitons {\displaystyle ~P_{1s}}, the nucleons acquire additional energy. This energy would be just enough for the star to lose mass due to evaporation of nucleons from the surface.

Electromagnetic field

The presence in vacuum of relativistic charged particles helps to explain mechanism of attraction and repulsion between the charges of different and opposite signs, [3] which acts similarly to the Fatio-Le Sage's mechanism for the force of gravitational attraction of masses. This implies the same form of laws in the Coulomb force for charges and in the Newton force for masses, as well as similarity of Maxwell's equations and equations of gravitational field in Lorentz-invariant theory of gravitation. [12]

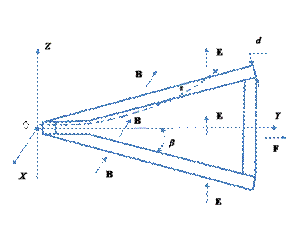
The interaction picture is shown in Figures 1, 2, 3.

Fig.1. The lines of motion of small particles of vacuum, which are a) positively charged, b) negatively charged, near two bodies one of which is neutral and the other is positively charged.

Fig.2. The lines of motion of small particles of vacuum which are a) positively charged, b) negatively charged, near two bodies, one of which is negatively charged and the other is positively charged.

Fig.3. The lines of motion of small particles of vacuum, which are negatively charged, near two positively charged bodies.

Figure 1 shows motion of small charged particles of vacuum near the two bodies, one of which is neutral and the other is positively charged. As can be seen, both positive and negative particles act symmetrically on the positively charged body, which does not result in emerging of any additional force in comparison with the force of gravitation. The same applies to the second neutral body. Figure 2 a) shows that the positive particles push the negatively charged body to the left, and Figure 2 b) shows that the negative particles push the positively charged body to the right (when the smallest particles pass through the body similarly to gravitons, they transfer their momentum to them). Consequently, both bodies will be attracted to each other.

Figure 3 shows the lines of motion of negative particles of vacuum near two positively charged bodies. Both bodies attract the negative particles and obtain an additional momentum from them, which leads to repulsion of bodies. The motion of positive particles of vacuum in Figure 3 is not shown. It is assumed that they are repelled from the bodies and therefore their interaction with them is weak. For two negatively charged bodies the interaction is similar to the one shown in Figure 3, only it is necessary to replace the signs of all charges. This results in repulsion of similarly charged bodies. The common in all the Figures is the fact that depending on the sign of the charge of two bodies the number of charged particles falling on the body changes so that after calculating the momentum transferred from these particles the electric force with required direction emerges. Thus, we reduce the interaction between the charges at a distance to the interaction by means of charged particles of vacuum.

The energy density of fluxes of the vacuum’s charged particles, responsible for occurrence of electric force between the charged bodies, in the model of cubic distribution of the fluxes of particles in space is equal to: [5]

{\displaystyle ~\varepsilon _{cq}={\frac {e^{2}}{\varepsilon _{0}\vartheta ^{2}}}=4\cdot 10^{32}} J/m3,

where {\displaystyle ~\varepsilon _{0}}  is electric constant, {\displaystyle ~e}  is elementary charge, {\displaystyle ~\vartheta =2.67\cdot 10^{-30}} m2 is cross-section of interaction of vacuum’s charged particles with nucleons.

The energy flux of vacuum’s charged particles in one direction is of the order of {\displaystyle ~2\cdot 10^{40}} W/m2. Estimation of concentration of the vacuum’s charged particles in the form of concentration of relativistically moving praons gives the value {\displaystyle ~n_{pr}=4\cdot 10^{87}} m–3, and Lorentz factor reaches the value {\displaystyle ~1.9\cdot 10^{11}}.

The limiting current density as the current density in vacuum in one direction, emerging from the flux of positively charged praons in case of cubic distribution, is equal to:

{\displaystyle ~j_{lim}=n_{pr}q_{pr}c=5.5\cdot 10^{39}} A/m2.

In books [3] [12] the assumption is made that some neutron stars – magnetars can have a positive electric charge of up to {\displaystyle ~Q_{s}=eS{\sqrt {\Phi P}}=5.5\cdot 10^{18}} C, where {\displaystyle ~e} is elementary electric charge and similarity coefficients are used in accordance with the dimensional analysis. The charge of the star can also be determined by the formula similar to the formula for strong gravitational constant. This gives the following:

{\displaystyle Q_{s}=M_{s}{\sqrt {\frac {4\pi \varepsilon _{0}G}{\beta }}},}

where the magnetar’s mass equals {\displaystyle ~M_{s}=1.35} solar masses, {\displaystyle ~\beta }  is the ratio of the proton mass to the electron mass.

In this case, the electric force of repulsion acting on one proton on the surface of the charged star would equal 55 N, which is much greater than gravitational force of attraction of the proton to the star. However the magnetar looks like a huge atomic nucleus consisting of a number of closely-spaced nucleons. The balance of attractive and repulsive forces, arising from strong gravitation in gravitational model of strong interaction, can be responsible for integrity of the atomic nuclei, as well as for the integrity of the charged neutron star. Besides, the proton charge and the magnetar charge are limiting values, which means that an increase in these charges would lead to destruction of these objects.

In a magnetar, the average concentration of nucleons is {\displaystyle ~n=2.2\cdot 10^{44}} m–3, and the average concentration of the positive charge is {\displaystyle ~\eta =4.7\cdot 10^{24}} m–3. In view of the Beer–Lambert law, the flux of gravitons decreases exponentially as it moves through the matter: {\displaystyle ~B=B_{0}\exp(-\sigma nx)},  here {\displaystyle ~B_{0}={\frac {dN_{0}}{dtd\alpha dA}}}  is the number of gravitons {\displaystyle ~dN_{0}} entering the matter from the vacuum through the area {\displaystyle ~dA}  over time {\displaystyle ~dt} from the solid angle {\displaystyle ~d\alpha } . Similarly, the flux of charged particles decreases exponentially as it moves through the charged matter: {\displaystyle ~B_{q}=B_{0q}\exp(-\vartheta \eta x)}.

Assuming that {\displaystyle ~x=2R_{s}=24} km, for the exponents it turns out: {\displaystyle ~\sigma nx=0.3} , {\displaystyle ~\vartheta \eta x=0.007} . It follows that if we put three neutron stars in the way of the flux of gravitons, the flux will reduce approximately by a factor of  {\displaystyle e_{n}}, where  {\displaystyle (e_{n}\approx 2.718)}is Euler's number as the base of the natural logarithm. But for the flux of charged particles of vacuum in order to reduce it noticeably we need to put in a line about 140 magnetars.

This difference in fluxes allows us to explain the saturation effect of the specific binding energy, when the nuclear binding energy per nucleon, depending on the number of nucleons in nuclei, first increases, reaching a maximum of 8.79 MeV per nucleon for the nucleus {\displaystyle {}_{28}^{62}{\textrm {Ni}}}, and then begins to decrease. [3] [17] For light nuclei the increase in the specific energy agrees well with the increase of the specific gravitational energy of the nucleus in strong gravitational field, when the energy increases in direct proportion to the square of mass and in inverse proportion to the radius of the nucleus. The saturation effect comes into play in the range of 17 to 23 nucleons, forming the nucleus. Besides, adding a new nucleon to the nucleus increases the energy not proportionally to the square of mass, but to a lesser extent. This is due to the fact that gravitons of strong gravitation cannot permeate the nucleus with a lot of nucleons, as is evident from the exponent. Each new nucleon is simply pressed to the nucleus from the outside by the strong gravitation, until for the large nuclei this force reaches the maximum, conditioned by the pressure of the graviton flux. However, the charged particles of the vacuum in these conditions have almost 50 times larger path length, and therefore the positive electrical energy of the nucleus’ protons further decreases the negative gravitational energy of the nucleus, making the main contribution into the observed decrease in the specific binding energy of massive nuclei.

In this model, the fluxes of charged particles of vacuum are the cause of the so-called displacement currents in the vacuum, which are proportional to the rate of change of electric field with the time. Here, an example is the chargeable capacitor, between the plates of which there appears a magnetic field, despite the absence of electron current in the capacitor.

Since electric constant remains the same and does not change during SPF symmetry transformation, and the gravitational constant has its own value at each level of matter, then the electromagnetic interaction can be considered primary with respect to gravitational interaction.

Interaction of vacuum’s particles with matter

The main problem of Le Sage’s theory is the problem of heating of bodies, both for the fluxes of gravitons leading to gravitation and for the fluxes of charged praons creating electromagnetic interaction at the nucleon level of matter. Actually, since the fluxes of gravitons and charged particles must transfer some part of their momentum to matter to give rise to gravitational and electromagnetic forces, it also seems that some part of the energy of these fluxes should turn into kinetic energy of motion of matter and thus heat it to high temperatures, which is not observed.

It turns out that there is such a mechanism possible, when the fluxes of smallest relativistic particles transfer some momentum to a body’s matter, but at the same time they almost completely conserve their energy and are re-emitted into the surrounding space without heating the body significantly. So, in physics fields are known that do not perform work on particles and do not change their energy. This is the magnetic field, as well as gravitational torsion field in covariant theory of gravitation, known as gravitomagnetic field in general theory of relativity. A relativistic charged particle, passing through the region of space with magnetic field, is deflected from the original direction of motion by the Lorentz force, in which case amplitude of the particle’s momentum and its energy do not change. Despite this, the pressure force from the particle is exerted on the source of the magnetic field. This happens because the momentum like any vector can change both in magnitude and in direction, and any change in the momentum is associated with the corresponding force.

The analogue of nucleons at the level of stars is a neutron star, and the fluxes of praons correspond to cosmic rays. The cosmic rays, passing close to a neutron star, will interact with the strong magnetic field of the star and be deflected by it. Obviously, if the flux of cosmic rays on one side of the star is stronger than on the others, then the stronger flux will start to shift the star due to the magnetic pressure. The same effect takes place also due to the gravitational torsion field, which is especially strong in rapidly rotating neutron stars and it interacts even with neutral fast-moving particles, since it does not act on the moving charge but on the momentum of particles.

The fluxes of praons moving in matter are influenced not only by magnetic fields of nucleons, but also by electric fields of uncompensated charges of individual protons and electrons. These fields also deflect the fluxes of praons without significant changes in the energy of praons, which is a consequence of potentiality of electric field. Actually, if the fluxes of positively charged praons fly towards the proton, they are first decelerated by electric field of the proton and decrease their energy, and then when they fly past the proton, they start accelerating from the proton under influence of the same field and increase their energy up to the previous level. The gravitational force acts on gravitons in a similar way.

With the help of the described mechanism the fluxes of gravitons and praons can create gravitational and electromagnetic interactions in matter of bodies without heating these bodies significantly. [5] Passing through matter the fluxes of gravitons and praons, consisting of a large number of tiny particles, act simultaneously on the nucleons, electrons and atomic nuclei, compressing them in direction of gradient of corresponding flux and creating gravitational and electromagnetic acceleration. The fact that interaction cross-section {\displaystyle ~\vartheta } characterizes both the electromagnetic interaction of fluxes of praons with nucleons and strong gravitation from the fluxes of gravitons at the level of nucleons, and is equal by the order of magnitude to the cross-section of nucleon, suggests that the interaction forces can actually emerge near the surface of nucleons. Here, the electric and gravitational fields, the magnetic field and the torsion field of nucleons reach the maximum and can effectively interact with the fluxes of praons and gravitons. As gravitons, leading to strong gravitation, are suggested graons as the particles that make up praons just as praons make up nucleons or as nucleons make up a neutron star. For graons in order to become gravitons they must be accelerated up to relativistic energies in the processes near the surface of praons.

According to the second problem of the Le Sage’s theory, during motion excess pressure of gravitons and charged particles in front should emerge drag effect, proportional to velocity of the bodies’ motion. As a result of resistance to the bodies’ motion from the fluxes of gravitons, long-term rotation of planets around the Sun would not be possible and the principle of free inertial motion in the absence of forces would not hold true. When a charged body moves in the fluxes of relativistic charged particles, both the momentum of the particles falling on the body at the front and the fluence of fluxes of these particles increase. This leads to an increase in the force at the front in proportion to the square of the particles’ energy.

On the other hand, the cross-section of the praons’ interaction with the matter should be directly proportional to the square of the de Broglie wavelength, and inversely proportional to the square of energy of praons. This dependence of cross-section in the quantum theory of elastic scattering is typical of ultrarelativistic photons – the greater their energy is, the weaker they interact with each other. At the same time, it is assumed that photons are composed of praons, and the interaction of praons with the electromagnetic field of nucleons is a special case of photon’s interaction on virtual photons. Since the force is proportional to momentum of the particles, their fluence and the interaction cross section, then the force remains unchanged both for a fixed and a moving body. Thus, the body can move by inertia and the decelerating force from the fluxes of charged particles of vacuum, proportional to velocity of motion, does not arise.

The problem of aberration in the Le Sage’s theory is illustrated by an example, in which in motion of two gravitationally bound bodies near each other it seems that in view of limited velocity of the gravitons’ motion, a certain additional force takes place. Indeed, while the gravitons moving from one body reach the second body, it will move in its path from the position that is dictated by the Newton’s theory of gravitation for instantaneous gravitation. As a result, the gravitons will reach the second body at some other angle to the path, which gives an additional force component. This problem has been considered for the case, when two bodies are moving synchronously in the direction perpendicular to the line connecting the bodies. [1] In this case it was shown that the problem of aberration of the gravitational force disappears, if we apply the relations of special theory of relativity to gravitons, which take into account that velocity of ultrarelativistic particles is not infinite and is almost equal to the speed of light. In both cases, for fixed and moving bodies, gravitons reach these bodies at the same angle with respect to the axes of the proper coordinate system.

The hypothetical problem of gravitational shielding in Le Sage’s theory suggests that if we place between two bodies the third body, it will lead to a more noticeable change in the forces between the bodies, than in case of the Newton's law of gravitation for three bodies. The measurements of possible Moon’s shielding of the Sun’s gravitational influence on the Earth during Solar eclipses do not find any deviation from the theory within the limits of measurement error. This situation is due to smallness of the cross-section of gravitons’ interaction with matter. This allows us to expand the exponents in expressions for the forces into binomials with sufficiently high accuracy and ensures the principle of superposition of gravitational forces for several bodies. A noticeable deviation occurs only for such dense objects as white dwarfs and especially for neutron stars. A similar situation is obtained for the case of electromagnetic interaction of bodies by means of charged vacuum particles, also leading to the principle of superposition.

Emergence of relativistic vacuum’s particles

We can distinguish in vacuum three components, one of which with the energy density {\displaystyle ~\varepsilon _{c}} is associated with strong gravitation and the rest energy of particles, determines the integrity of nucleons and atomic nuclei, and is mainly responsible for the inertia of bodies. Another component with the energy density {\displaystyle ~\varepsilon _{s}} is responsible for ordinary gravitation, and the third component in the form of charged particles with the energy density {\displaystyle ~\varepsilon _{cq}}  leads to electromagnetism. Each component makes its own contribution to the mass of bodies.

Based on the principles of Infinite Hierarchical Nesting of Matter, the densest objects at each level of matter are assumed as sources of relativistic charged particles of vacuum – neutron stars and magnetars, nucleons and atoms, praons as the components that make up nucleons, etc. These objects emit neutrinos, photons and high-energy cosmic rays that can make contribution to electrogravitational vacuum at all levels of matter. As a result, the main sources of vacuum relativistic particles at a certain level of matter are the emissions from the densest objects at the lower levels of matter. For example, the core of a neutron star is constantly heated under action of incident fluxes of gravitons, having a temperature up to {\displaystyle ~T_{s}=2.8\cdot 10^{11}} K. The kinetic temperature at the surface of neutron stars is determined from observations and has typical value of about {\displaystyle ~10^{6}} K, and thermal luminosity rarely exceeds {\displaystyle ~10^{26}} J/s. The stellar core is heated enough to constantly emit neutrino fluxes, escaping from the star and flowing into surrounding vacuum. At the time of formation of a neutron star or during its transformation into a magnetar with reconfiguration of magnetic moment, intense neutrino fluxes directed by the magnetic field (due to the connection between total magnetic field and magnetic moments of nucleons) arise, which will act effectively at a higher level of matter than the stellar level.

Neutron stars generate not only neutrino fluxes, but also give rise to cosmic rays, as it follows from the study of supernova remnants. The proton energy on surface of charged magnetar can reach {\displaystyle ~E_{pe}={\frac {eQ_{s}}{4\pi \varepsilon _{0}R_{s}}}=6.6\cdot 10^{5}} J  or  {\displaystyle ~4\cdot 10^{24}} eV, here {\displaystyle ~Q_{s}=5.5\cdot 10^{18}} C is the charge of magnetar, {\displaystyle ~\varepsilon _{0}}  is the electric constant, {\displaystyle ~R_{s}=12}  km is the star radius.

For comparison, the highest recorded values of cosmic ray energies per 1 nucleon according to estimations are of the order of {\displaystyle ~6\cdot 10^{19}} eV, reaching the Greisen–Zatsepin–Kuzmin limit, and so is the maximum recorded energy of photons and neutrinos. Oh-My-God particle had energy of the order of {\displaystyle ~3\cdot 10^{20}} eV. If we assume that the cosmic rays are accelerated from the surface of the discon surrounding the magnetar, then for the energy of emitted particle with one elementary charge we can write:  {\displaystyle ~E_{d}={\frac {eQ_{s}}{4\pi \varepsilon _{0}R_{d}}}=11} J or {\displaystyle ~6.7\cdot 10^{19}} eV, where {\displaystyle ~R_{d}=7.4\cdot 10^{8}} m denotes the stellar Bohr radius, while {\displaystyle ~R_{d}=Pr_{B}}, where {\displaystyle ~r_{B}} is the Bohr radius in hydrogen atom, {\displaystyle ~P} is the coefficient of similarity in size. The coincidence of energy {\displaystyle ~E_{d}}  with the energy of the recorded particles suggests that the possible source of cosmic rays can actually be magnetars with discons.

In this picture the energy of gravitational field is transformed by neutron stars with the help of different mechanisms into energy of particles (neutrinos, protons, photons), the high energy of which causes the high penetrating ability of these particles. Applying this to other levels of matter, we find the source of relativistic particles of vacuum – it is the emissions from the densest objects, such as nucleons and neutron stars, including the emission of such objects as atoms. The presence of constant electric charge in the magnetar allows it to generate cosmic rays and various particles for a long time – similarly to a proton, which is practically eternal. Thus, if each level of matter would have a long lifetime, it will be enough to transform the energy of the gravitons at the lower levels of matter into energy of charged particles and gravitons, which will act at the higher levels of matter.

Photons

Main article: Substantial photon model

In substantial electron model the electron in the form of a disk is considered, in which the charged matter rotates differentially, and ensures the magnetic moment of the electron. In addition, the electron spin is explained as a result of shift of the disk’s center relative to the nucleus and rotation of this center in addition to the matter rotation in the electron cloud. If the electron transits into the quantum state with lower energy, it emits a photon, which carries with it the angular momentum that is proportional to the Dirac constant. In this process, the scattering of charged particles of vacuum on the electron disk, taking into account the action of magnetic and electric fields in wave zone, leads to formation of a photon as an object preserving its structure for a long time.

In papers, [5] [6] a model of a photon emitted in an atomic transition in a hydrogen-like atom is considered. Associating the photon parameters and its structure with the parameters of the emitter – the charged electron disk, it was possible to determine the charge to mass ratio for the particles that make up the photon. As a result, it turned out that photons consist of praons of very high energies, comparable to the energies that cosmic rays would have if these rays emerged at the nucleon level of matter near the protons. These relativistic praons must form the basis of charged particles of vacuum, leading to electromagnetic interaction through the mechanism of Lesage. Indeed, in interaction of praons of vacuum with electron in atomic transition, the twisting of praons takes place under action of fields along the axis of electron disk, and the appearing photon carries away the excess angular momentum of the electron from the atom. Meanwhile, part of praons of vacuum is part of photon, so that the speed of the photon actually is the speed of praons in the fluxes of particles of the vacuum and close to the speed of light.

In contrast to chaotic motion of praons in vacuum, the praons in a photon are rigidly bound to each other by both electromagnetic and gravitational forces. The situation here is similar to the situation with the nucleons, which only in special circumstances can form extremely stable formations – the atomic nuclei. According to gravitational model of strong interaction, the nucleons in atomic nuclei are attracted to each other by strong gravitation and repel each other by means of gravitational torsion field, arising from the rapid rotation of the nucleons. In order to form the nucleus, the nucleons must interact with each other only in a strictly defined orientation of the spins and magnetic moments and must have sufficient initial energy that allows rotating the nucleons up to the desired rotation speed by means of gravitational induction. The praons in photon can interact with each other in a similar way, and for the praonic level of matter, the gravitational constant reaches {\displaystyle ~G_{pr}=1.752\cdot 10^{67}} m3•s–2•kg–1. In gravitational field with this large gravitational constant, the praons of photon can form sufficiently rigid structure, so that the photon could fly large cosmic distances without decaying.

The substantial photon model suggests that photons have magnetic moment and rest mass. Thus, for a photon, emerging in a hydrogen atom when an electron goes from the second level to the first level in the Lyman series, the invariant mass of praons that make up the photon is equal to  {\displaystyle ~m_{ph}=1.6\cdot 10^{-42}} kg  or {\displaystyle ~9\cdot 10^{-7}} eV/s2 in energy units, where ~c^{2} is the square of the speed of light.

Strong interaction

According to gravitational model of strong interaction, strong gravitation acts between nucleons, holding them together. The nucleons in atomic nuclei are attracted to each other due to strong gravitation and repel each other due to the gravitational torsion field arising from rapid rotation of nucleons and leading to spin-spin and spin-orbital forces. In Lorentz-invariant theory of gravitation the torsion field emerges similarly to magnetic field in electromagnetism, and in general theory of relativity it corresponds to gravitomagnetic field. Taking into account that the torsion field and gravitational field strength are the components of gravitational tensor, strong interaction at the nucleon level of matter is explained by strong gravitation. At the same time, in contrast to Standard Model, strong interaction must be acting not only between hadrons, but also between leptons.

Indeed, in the theory of Infinite Hierarchical Nesting of Matter, elementary particles differ from each other by the physical state of their matter and consist of praons and praelectrons. Similarly, the matter of objects at the stellar level of matter (the matter of planets, main sequence stars and other ordinary stars, white dwarfs and neutron stars) consists of nucleons and electrons in different phase states. Strong gravitation actually acts on every praon of an elementary particle regardless of type of this particle, just as ordinary gravitation at the Earth’s surface acts either on individual nucleons or on the same nucleons as part of a test body with any state of matter.

At each basic level of matter there is its own gravitation, which is characterized by its own gravitational constant, and there is also electromagnetic interaction between the charges. Since gravitational and electromagnetic interactions can be explained by the action of relativistic particles of electrogravitational vacuum, then strong interaction at each level of matter turns out to be a consequence of corresponding gravitational interaction, and not a substantially different type of interaction. In particular, it is assumed that strong gravitation and hence strong interaction at the nucleon level of matter are caused by the action of fluxes of relativistic graons present in electrogravitational vacuum and acting on matter of elementary particles. [5]

Weak interaction

The role of weak interaction reduces to the fact that under action of fundamental forces and strong interaction of objects after their formation take place a slow transformation of matter. For example, a neutron in a very large time by the standards of atomic processes turns into a proton, an electron and a neutrino. The transformation of matter can be significantly accelerated by external factors. Thus, the incident on an elementary particle a neutrino can easily convert matter of the particle and cause it to decay into other particles.

In substantial neutron model, free neutron decay is analyzed using a stellar model in the form of a neutron star. It is concluded that slow transformation of stellar matter occurs due to cooling of the star and the subsequent beta decays of the matter’s neutrons. The neutron beta decay is a consequence of the fact that individual neutral praons in the neutron’s matter undergo their own beta decays and turn into positively charged praons, praelectrons and antineutrinos of the praon level of matter. All this leads to the fact that after a great number of such decays positively charged praons and negatively charged praelectrons are accumulated in the neutron shell. When the magnetic field from the charged praons exceeds the magnetic field from the neutral praons, a catastrophic reconfiguration of the total magnetic field occurs in the neutron with ejection of negatively charged part of the shell. Thus, a neutron becomes a proton and emits an electron and an electron antineutrino. In fact, this antineutrino represents the sum of praneutrinos and praantineutrinos emitted by a set of praons of the neutron’s matter in the course of the neutron decay.

It follows from the above that the processes of weak interaction at a certain basic level of matter again are reduced to the processes of weak interaction, but already at a lower level of matter. At the same time, the role of relativistic particles of electrogravitational vacuum at all levels of matter is reduced to dynamic action on the matter’s particles, which we consider as gravitational and electromagnetic interactions, and at the level of nucleons it is represented as strong interaction. The fact that the long-term dynamic action of vacuum’s particles on objects finally can lead to a rapid transformation of their matter and to emission of the particles like neutrinos and antineutrinos is perceived by us as a manifestation of weak interaction. This also includes reverse processes, when neutrinos and antineutrinos themselves interact with various objects and transform their matter with subsequent decay.

Neutrinos

According to the picture of weak interaction in the model of electrogravitational vacuum, neutrinos and antineutrinos, similarly to photons, are the vacuum’s particles. On the other hand, neutrinos and antineutrinos themselves must consist of the main objects of the respective levels of matter. In particular, it is assumed that neutrinos and antineutrinos of the nucleon level of matter consist of graons, in contrast to photons, which consist of praons. [5]

Indeed, during the neutron beta decay an electron antineutrino is emitted, which consists of the fluxes of electron praneutrinos and praantineutrinos resulting from the beta decays of praons of the nucleon’s matter. In the course of the beta decay of each praon, only graons and even smaller particles of lower levels of matter can become part of the emerging praneutrino or praantineutrino.

The analysis carried out in the book [3] shows that the electron antineutrino has the right-handed helicity and is emitted mainly in direction of e spin of decaying neutron. This means that the fluxes of electron praneutrinos and praantineutrinos, forming an electron antineutrino, are twisted to the right. If the same fluxes in other decays are twisted to the left, then an electron neutrino emerges. Between rotating praneutrinos and praantineutrinos, consisting of graons, there is strong gravitation at the matter level of graons, which holds them together as part of neutrinos or antineutrinos and ensures their long-term stability.

Muon neutrinos and antineutrinos emerge from the decay of charged pions into muons, as well as from the decay of muons into an electron (positron) and an electron antineutrino (neutrino), depending on the sign of the muon charge. In particular, if magnetic moment of the positive pion coincides in direction with its rotation, then when the pion decays, a muon neutrino, having the left-handed helicity, should be emitted mainly in the direction of the south pole of the magnetic field and against the pion spin, with the helicity corresponding in direction to the rotation of the pion’s matter.

Similarly to electron neutrinos, a muon neutrino consists of polarized fluxes of electron praneutrinos and praantineutrinos, resulting from the weak interaction reactions in the matter of decaying particles. The difference between electron and muon neutrinos is mainly associated with the difference in their energy and the peculiarities of those objects that emit these neutrinos. It is due to the similar composition of their constituent parts that electron and muon neutrinos have the ability to transform into each other in neutrino oscillations.

Cosmology

In observable universe, the following properties are found:

The above-mentioned properties of observable universe should be explained in every cosmological theory. For example, the most distant regions of observable universe are so far from each other that during the estimated time of its existence they would not be able to interact with each other and to achieve the state of uniformity and isotropy. The processes of interaction between particles and wave quanta in the course of evolution of observable universe must be such as to lead to the observed ratio of photons to nucleons.

According to Lambda-CDM model, in visible Universe concentration of baryons is of the order {\displaystyle ~n=0.13}  nucleons per cubic meter. From the ratio {\displaystyle ~\sigma nx\approx 1}  at a given concentration of nucleons and the known value of cross section for interaction of gravitons with matter for ordinary gravitation {\displaystyle ~\sigma =5.6\cdot 10^{-50}} m2  it is possible to estimate the free path length of gravitons: {\displaystyle ~x=1.4\cdot 10^{50}} m. This value is 23 orders of magnitude greater than the visible size of Universe, which is estimated by the value of 14 billion parsecs or {\displaystyle ~4\cdot 10^{27}} m.

Similarly may be estimated the length of free path of charged particles of vacuum in cosmic space, taking as the charge concentration in a first approximation the value {\displaystyle ~\eta =0.13} of the elementary charge per cubic meter, which is equal to the average concentration of baryons in the Universe. This approach gives only the minimum value of free path length, since on the average the matter in the Universe is neutral, and {\displaystyle ~\eta }  must reflects the average concentration of total charge of Universe. From the ratio {\displaystyle ~\vartheta \eta x\approx 1} at a given concentration of charges and the value {\displaystyle ~\vartheta =2.67\cdot 10^{-30}} m2, the free path length of charged particles is {\displaystyle ~x=2.9\cdot 10^{30}} m. This value is 3 orders of magnitude greater than the visible size of Universe. Consequently, the charged particles and gravitons can easily reach our Universe from a distance.

From the standpoint of similarity of matter levels, the set of all stars in visible Universe corresponds to extremely rarefied atomic gas. At first glance, this rarefied gas of stars, even in view of the lower levels of matter, cannot create this energy density of graviton field {\displaystyle ~\varepsilon _{c}=7.4\cdot 10^{35}}J/m3. But in remote areas of cosmic space the density of matter can be much greater and reach such values, that it can generate the necessary energy density of graviton field, reaching our Universe.

The effects of redshift of the galaxy spectra and attenuation of emission from distant supernovae can be explained by the fact that the light is scattered on new particles or nuons. [18] These particles are neutral particles of muon type, which emerged naturally in the same way as white dwarfs emerge in the course of stellar evolution. The sizes of nuons and their concentration in space, according to Infinite Hierarchical Nesting of Matter, are so just such that can explain the scattering of light. Nuons also explain the appearance of background emission and the effects attributed to dark matter. If we admit the existence of nuons, then the most important arguments in favor of the Big bang model become useless. If Universe has existed longer than 13.8 billion years, then gravitons could have got into our Universe from outside and carried out their action here.

This shows that 61% of all praons are part of nucleons, and the rest 39% form nuons or exist separately. The same proportion remains at the level of stars: 61% of all nucleons over time will be part of neutron stars, and the rest of nucleons remain either as a gas or as the matter of white dwarfs. Consequently, concentration of free protons in visible Universe must be of the same order as the averaged over the entire space concentration of nucleons in stars, that is of the order of concentration of baryons {\displaystyle ~n=0.13}  m–3, according to Lambda-Cold Dark Model. With this in mind, the product of concentration of baryons and the binding energy of a neutron star in calculation per nucleon give us the estimate of maximum energy density of radiation in cosmic space: {\displaystyle ~nE_{b}=10^{-12}} J/m3. Indeed, the energy density in the relic radiation equals {\displaystyle ~4\cdot 10^{-14}} J/m 3, and the energy density in stellar radiation, magnetic fields and cosmic rays is of the same order of magnitude, as well as kinetic energy of motion of gas particles. The sum of these energy densities does not exceed the maximum energy density {\displaystyle ~nE_{b}}.

Thus, the electrogravitational vacuum of Universe, filled with the same particles regardless of the observation point, due to unified scheme of evolution of matter’s particles at different levels of matter, allows us to explain the uniformity and entropy of photons in observable universe. In this case, the predominance of baryons over antibaryons, which seems surprising in the hot Big Bang model, can occur due to significant difference in probabilities of emergence of particles and antiparticles in the model of cold and long-term evolution of Universe. As for the observed flatness of space, it is a consequence of low mass density of the observable Universe.

Extended special theory of relativity

At each point of electrogravitational vacuum, such isotropic reference frame can be chosen that in it, on the average, the same and mutually opposite fluxes of vacuum particles would pass through any unit area per unit time. Thus, there will be no initially selected direction of motion of these particles. In an isotropic reference frame, the speed of light is the same in all directions. In extended special theory of relativity (ESTR), the contradictory in its essence postulate about the constancy of the speed of light and its independence from the motion of light sources and from the motion of observer is replaced by a physically more understandable postulate about the existence of an isotropic reference frame. This leads to the fact that all relations of the special relativity can be derived in new axiomatics. As a result, the constancy of the speed of light in inertial reference frames is derived as one of the consequences of ESTR.

General field

The electrogravitational vacuum manifests itself by the fact that neutral and charged particles present in it, when acting on the bodies’ matter, lead to gravitational and electromagnetic forces between these bodies. These forces ensure both the integrity of bodies and observed hierarchy of matter levels. In addition, the corresponding charge and mass, as a measure of inertia, can be attributed to each body. Standard description of electromagnetic field is its representation in the form of vector four-dimensional field with electromagnetic four-potential {\displaystyle ~A_{\mu }} . A similar approach for gravitation gives the vector covariant theory of gravitation, defined with the help of gravitational four-potential {\displaystyle ~D_{\mu }} . In addition to electromagnetic and gravitational fields, other fields can be detected in matter of macroscopic bodies, for example, the pressure field, the dissipation field, and the acceleration field. The four-potentials {\displaystyle ~\pi _{\mu }}, {\displaystyle ~\lambda _{\mu }} and {\displaystyle ~U_{\mu }}  can be attributed to these fields, respectively, and these fields can be considered as vector fields. [19] [20]

In contrast to a scalar field, a vector field takes into account dependence of the four-potential on velocity of the field source’s motion, and therefore it provides a more accurate description of reality. As a result, all vector fields are either direct or indirect consequences of action of the electrogravitational vacuum’s particles on matter, and we can assume that there is a certain general field, which has, as its basis, a single source associated with the vacuum. [21] To emphasize the relative independence of gravitational and electromagnetic field, the general field was divided into two main components. [22] One of them is the mass component of general field, the source of which is the mass four-current {\displaystyle ~J^{\mu }} . The source of the second one – the charge component of general field – is the charge four-current {\displaystyle ~j^{\mu }} . The mass component of general field contains gravitational field, acceleration field, pressure field, dissipation field, fields of strong and weak interaction, and other vector fields. The charge component of general field represents the electromagnetic field. The four-potential of the charge component of general field is the electromagnetic four-potential {\displaystyle ~A_{\mu }} . The four-potential of the mass component of the general field is equal to the sum of four-potentials of corresponding fields:

{\displaystyle ~s_{\mu }=D_{\mu }+U_{\mu }+\pi _{\mu }+\lambda _{\mu }+g_{\mu }+w_{\mu },}

where the four-potentials {\displaystyle ~g_{\mu }}  and {\displaystyle ~w_{\mu }} describe the fields of strong and weak interactions in macroscopic bodies, and effects associated with these fields.

In view of its definition, none of general field’s components can have the energy density that would exceed the field mass-energy limit as the energy density of corresponding component of electrogravitational vacuum.

Preferred reference frames

Mach's principle is closely related to the assertion about possibility of existence of a preferred (privileged) reference frame defined by any objects of Universe. It is assumed that change in motion of any body relative to the preferred reference frame caused by the action of another body leads to an inertia force acting from the side of the first body to the second and changing its state of motion. So, inertial mass is detected in each body, the product of which on acceleration of the body is equal to the force of inertia.

The following statements are known that describe the preferred reference frame:

Fluxes of gravitons, arriving at an arbitrary point in space, depend on remote sources of gravitons, and therefore cannot always be exactly the same from all sides, even taking into account the averaging of action of a huge number of such sources. Following the fluctuations of the graviton fluxes, an isotropic reference frame at a given point must change its velocity in order to be considered isotropic. As a result, isotropic reference frames at different points in space can have different velocities relative to each other. This means that in the general case there is no single preferred reference frame for the entire space of Universe and therefore there is no absolute simultaneity of events.

However, the averaging procedure allows us to move from microscopically set values to their average values at the macro level that characterize the system as a whole. It is known that on a scale of more than 100 Mpc, our Universe looks like a uniform system. When averaging at such scales, we can talk about a certain global preferred reference frame, which is isotropic in the first approximation. With the same degree of approximation in such frame of reference, the absolute simultaneity of events occurring on a scale of more than 100 Mpc is achieved. In all other cases, we can only have the relative simultaneity of events.

Cosmic microwave background radiation can be considered as one of the components of electrogravitational vacuum. The inhomogeneity and a high degree of isotropy of the CMB coming to the Earth make it possible to accurately determine the preferred reference frame associated with this radiation. This reference frame moves relative to the Sun at a speed of the order of 370 km/s in the direction opposite to the direction to the constellation Leo.

A global preferred reference frame, defined by the supposed single dynamic medium of reference, was introduced in an article written by Olivier Pignard. [23]

The indicated dynamic medium affects the surrounding bodies in approximately the same way as the action of graviton fluxes of electrogravitational vacuum, leading to the effect of gravitation. The following features of the dynamic medium are postulated:

1. This medium is a medium for propagation of light.

2. The speed of light varies near massive bodies.

3. Bodies affect the dynamic medium so that it manifests itself in the form of a curvature of space-time of the general theory of relativity. This means that test particles and photons accordingly change their motion near massive bodies.

4. Near the bodies fluxes of the given medium arise towards the center of these bodies. The speed and acceleration of such a flux are given by the formulas:

~V_{f}={\sqrt {{\frac {2GM}{r}}}},\qquad \qquad A_{f}={\frac {GM}{r^{2}}},

where  ~G  is the gravitational constant, ~M is the body mass, ~r is distance from center of the body to the point of observation outside the body.

The velocity ~V_{f}  of the dynamic medium flux affects the rulers and clocks that are stationary relative to the massive body in the same way as if these rulers and clocks moved in inertial reference frame with the same velocity ~V_{f}  in the absence of the massive body. This means that in both cases, the same relativistic effects appear that reduce the size of the rulers and slow down time of the clock, regardless of whether the flux of the dynamic medium moves relative to the rulers and the clock, or the rulers and the clock themselves move relative to the dynamic medium. 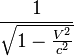In particular, relativistic effects due to movement at a speed ~V of a certain reference frame in an inertial reference frame depend on the Lorentz factor  ~{\frac {1}{{\sqrt {1-{\frac {V^{2}}{c^{2}}}}}}} . If we put ~V=V_{f} , then instead of the Lorentz factor in general relativity, the equivalent value ~{\frac {1}{{\sqrt {1-{\frac {2GM}{rc^{2}}}}}}}  appears.

The above features of the dynamic medium are in complete agreement with the properties of electrogravitational vacuum, in which photons are formed from relativistic vacuum particles and therefore move almost at the speed of light, just like gravitons. In the Lesage model, the graviton flux incident on a body from a certain direction always exceeds the oncoming graviton flux passing through the body from the opposite direction due to interaction of gravitons with matter and their partial scattering and absorption. This just corresponds to the fact that there arises a total flux of gravitons, which can be modeled as some centripetal directed graviton flux falling from the outside onto any body with the velocity  ~V_{f}.

The flux of a dynamic medium considered above can be considered as total flux of gravitons acting on rulers and clocks and leading to relativistic effects of length contraction and time dilation depending on the relative speed of the rulers and clocks in the isotropic reference frame. In this case, the special theory of relativity usually considers the movement of rulers and clocks in inertial frames of reference moving with an arbitrary constant speed relative to a globally isotropic frame of reference with slightly massive bodies that weakly affect graviton fluxes. If the bodies are massive, it is necessary to take into account the general relativity and distortion of the fluxes of gravitons near such bodies. In this case, we can assume that the velocities of numerous isotropic reference frames are directed towards massive bodies. Although the rulers and the clock may be stationary relative to a body, they will be in motion relative to the local isotropic reference frame at the location of the rulers and the clock. This leads to relativistic effects in gravitational field.

As for the relativistic effect of changing the speed of light near massive bodies, it is closely related to the procedure of spatio-temporal measurements by means of light in a light clock, when the bi-directional motion of the light signal along a closed path is taken into account. This effect appears for a coordinate observer, that is, for a remote external observer in an inertial reference frame that is stationary relative to the body, while for a local observer located at the point of measurement of the speed of light, the speed of light does not change.

At the same time, the light source in the light clock should not generate a single narrow beam, but a sufficiently wide light front so that at least part of this front reaches the reflector and returns back to the receiver located next to the light source. Indeed, the relative motion of the measuring system in an isotropic reference frame can lead to a deviation of a narrow light beam from the direction of the moving reflector and to signal loss in the receiver.

A change in the speed of light near massive bodies should be considered as an apparent effect, similar to the apparent (not real) reduction in body size in the direction of its movement. Other apparent effects include a length contraction in gravitational field for the coordinate observer and transformation of a moving sphere into a Heaviside ellipsoid according to the special theory of relativity.

In the model of electrogravitational vacuum, ordinary photons are formed from fluxes of relativistic praons under action of strong fields near elementary particles. In this case, the speed of the photons should be less than the speed of motion of the praons, since the photons not only move in a straight line, but also rotate. Upon transition to the underlying level of matter of graons, it becomes clear that the speeds of relativistic graons are higher than the speeds of praons, and photons consisting of graons move faster than ordinary photons, as can be seen from the increase in the Lorentz factor. The speeds of all these particles do not exceed the speed of light. 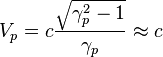In particular, if  ~\gamma _{p}  is Lorentz factor of a relativistic particle, then the speed of this particle is   ~V_{p}=c{\frac {{\sqrt {\gamma _{p}^{2}-1}}}{\gamma _{p}}}\approx c .  It turns out that the speed of light is the limit value for the speed of motion of relativistic vacuum particles, including photons at all levels of matter. In this sense, the speed of light becomes a fundamental quantity. Based on the fact that gravitational waves are waves of graviton fluxes in the form of praons, and photons are composed of praons and move slower than praons, the propagation speed of the gravitational signal can slightly exceed the speed of electromagnetic signal.

Spaceship Engine

Fig.1. A spacecraft engine using energy of electrogravitational vacuum. The figure shows a section of the engine's working chamber in the form of a truncated cone. The quantity d is the thickness of the cone walls, the angle \beta  denotes the cone opening angle, the electric field {\mathbf {E}} is directed along the OZ axis, the magnetic field {\mathbf {B}} is directed against the OX axis, the thrust force {\mathbf {F}} accelerates the engine along the OY axis of coordinate system. The dashed line shows trajectory of a positively charged vacuum particle, s specifies the length of the particle's path in the cone wall.

Based on the idea of electrogravitational vacuum, taking into account the previously discovered physical properties of vacuum particles and the way they interact with charged matter, [2] [5] it becomes possible to explain operating principle of an engine that uses vacuum energy. [24] The working fluid in such engine is the fluxes of relativistic vacuum particles that penetrate the engine from all sides. Under action of electric and magnetic fields directed perpendicular to each other, the Lorentz force arises, and the charged particles of vacuum change their trajectories in working chamber of the engine. The shape of the working chamber is a cone truncated on both sides. The ratio of amplitudes of electric field strength and magnetic field induction in the working chamber can be selected in such a way that some of vacuum particles will pass through the open ends of cone without interacting with substance of the cone walls. Another part of vacuum particles, passing along the axis of the cone from the opposite side of the cone, will be deflected by the Lorentz force from this axis and will therefore be able to pass through the walls of the cone. As a result of interaction of the vacuum particles with electric charges in substance of the walls, some particles will transfer their momentum to the substance. Thus, the engine as a whole receives a momentum, due to which the thrust force of the engine arises. The calculation makes it possible to determine the minimum thrust force ~F_{{min}} of the engine in the case when one electric charge equal in magnitude to elementary electric charge appears on the path of vacuum particles in substance of the walls of working chamber. For the value ~F_{{min}} the obtained value is 724 N, which is comparable with the minimum thrust force of 1390 N in the engine described in the article. [25]

References

  1. 1.0 1.1 1.2 Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009). http://dx.doi.org/10.5281/zenodo.890886.
  2. 2.0 2.1 2.2 2.3 2.4  Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
  3. 3.0 3.1 3.2 3.3 3.4 3.5 Sergey Fedosin. The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9. (2014).
  4. Fedosin S.G. The Force Vacuum Field as an Alternative to the Ether and Quantum Vacuum. WSEAS Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN: 1991‒8747 / 2224‒3429, Volume 10, Art. #3, pp. 31-38 (2015). http://dx.doi.org/10.5281/zenodo.888979.
  5. 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7  Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.
  6. 6.0 6.1 6.2 Fedosin S.G. The substantial model of the photon. Journal of Fundamental and Applied Sciences, Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.
  7. Fedosin S.G. On the structure of the force field in electro gravitational vacuum. Canadian Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp. 5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206.
  8. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
  9. Wang Zhongxiang, Chakrabarty Deepto, Kaplan David L. A Debris Disk Around An Isolated Young Neutron Star. Nature, Volume 440, pages 772–775 (2006). arXiv: astro-ph / 0604076 v1.
  10. Ü. Ertan et al. On the Evolution of Anomalous X-ray Pulsars and Soft Gamma-ray Repeaters with Fall Back Disks. ApJ, Vol. 702, pp. 1309 (2009). https://dx.doi.org/10.1088/0004-637X/702/2/1309.
  11. Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
  12. 12.0 12.1 12.2 Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1.
  13. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451.
  14. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
  15. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
  16. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12.
  17. Fedosin S.G. The Principle of Proportionality of Mass and Energy: New Version. Caspian Journal of Applied Sciences Research, Vol. 1, No 13, pp. 1-15 (2012). http://dx.doi.org/10.5281/zenodo.890753.
  18. Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp. 3-13 (2012). http://dx.doi.org/10.5281/zenodo.890806.
  19. Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
  20. Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13‒24 (2015). http://dx.doi.org/10.5541/ijot.5000034003..
  21. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
  22. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
  23. Pignard O. Dynamic medium of reference: A new theory of gravitation. Physics Essays, Vol. 32(4), pp. 422-438 (2019). http://dx.doi.org/10.4006/0836-1398-32.4.422.
  24. Fedosin S.G. The Principle of Operation of an Engine That Draws Energy from the Electrogravitational Vacuum. Jordan Journal of Physics, Vol. 17, No. 1, pp. 87-95 (2024). https://doi.org/10.47011/17.1.8.
  25. Leonov V.S., Baklanov O.D., Sautin M.V., Kostin G.V., Kubasov A.A., Altunin S.Y., Kulakovsky O.M. Non-rocket non-reactive quantum engine: ideas, technology, results, prospects. Aerospace Sphere Journal, No. 1 (98). pp. 68-75 (2019). http://dx.doi.org/10.30981/2587-7992-2019-98-1-68-75. (In Russian).

See also

External links

 

Source: http://sergf.ru/even.htm

On the list of pages