На русском языке

 

Characteristic speed

From Wikiversity

 

Characteristic speed is a physical quantity characterizing the average speed of motion of particles inside a single body or a particle system at rest. The ratio of the characteristic speeds of similar objects allows us to find the coefficient of similarity in speeds between different levels of matter in Infinite Hierarchical Nesting of Matter. For the nucleon form of matter the characteristic speed does not exceed the speed of light.

Definition

The characteristic speed is estimated by the formula:

C_{x}={\sqrt {{\frac {|E|}{M}}}},

where  |E| denotes the absolute value of the total energy of the body (particle system), M is the body mass.

If we take into account that the mass–energy equivalence is the principle of proportionality between energy and mass, then the square of the characteristic speed is the factor that connects these quantities in one formula:  |E|=MC_{x}^{2}. Due to its definition in terms of energy and mass, the characteristic speed can differ from the average speed of the system’s particles, being found in other ways and depending on the mode of averaging.

Connection with the escape velocity

For a sufficiently large body of uniform density with the radius R, which is spherical under the action of gravitational force, the absolute value of the total energy, according to the virial theorem, is equal to the half of the absolute value of gravitational energy |E_{g}|. It gives the following expression:

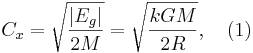
C_{x}={\sqrt {{\frac {|E_{g}|}{2M}}}}={\sqrt {{\frac {kGM}{2R}}}},\quad (1)

where  G is the gravitational constant,  k=0.6  for a uniform ball and increases when the density at the center of the ball is greater than the average density.

Let us consider now the process, in which the matter from infinity with zero initial speed is transferred into some space region and is superimposed on each other, so that in the end the ball under consideration is formed. Suppose  ~r is the current radius of the ball in its growth,  M(r)={\frac {4\pi \rho _{0}r^{3}}{3}} is the mass of the growing ball as a function of the current radius,  ~\rho _{0}  is the mass density. The work  ~dA done on the transfer of the layer with the mass  ~dM=4\pi \rho _{0}r^{2}dr  from infinity to the growing ball is equal to the work of the gravitational force or to the product of mass and gravitational potential of the ball’s surface:

dA={\frac {GM(r)dM}{r}},\quad A={\frac {16\pi ^{2}G}{3}}\int _{{0}}^{{R}}\rho _{0}^{2}r^{4}\,dr={\frac {kGM^{2}}{R}}.\quad (2)

Therefore, the work  A is equal by its absolute value to the doubled total energy  |E| and the gravitational energy  |E_{g}|, so that the characteristic speed equals:  C_{x}={\sqrt {{\frac {A}{2M}}}}. On the other hand, the product of the mass  dM and the gravitational potential is equal to the kinetic energy of falling of this mass on the ball with the current mass  M(r). This gives:

dA={\frac {dMv_{3}^{2}(r)}{2}},\quad {\frac {GM(r)}{r}}={\frac {v_{3}^{2}(r)}{2}},\quad A=\int _{{0}}^{{R}}{\frac {v_{3}^{2}(r)}{2}}\,dM.

In view of (1) we also obtain:

2C_{x}^{2}={\frac {kGM}{R}}={\frac {A}{M}}={\frac {1}{M}}\int _{{0}}^{{R}}{\frac {v_{3}^{2}(r)}{2}}\,dM={\frac {1}{2}}\overline {v_{3}^{2}(r)},

C_{x}={\frac {1}{2}}{\sqrt {\overline {v_{3}^{2}(r)}}},

where  \overline {v_{3}^{2}(r)} indicates the averaged over the ball’s volume square of the speed. We will take into account now that the speed  ~v_{3}(r) actually is the third escape velocity, required to remove some mass to infinity from the surface of the ball with the current radius  ~r in the process of the ball’s growth. Then the characteristic speed of the ball in general represents half of the square root of the mean square of the third escape velocity, averaged over the entire volume of the ball.

The characteristic feature of the gravitational field inside the uniform ball is that the field is directed radially towards the center of the ball. Besides, at the arbitrary current radius  ~r the field depends only on the mass inside of this radius, but not on the mass of the outer shell. Consequently, if there were no outer shell and it did not impede the motion of a test body, the gravitational acceleration of the test body would equal the centripetal acceleration, so that the body would rotate around the mass  ~M(r) under the action of gravitation:

{\frac {GM(r)}{r^{2}}}={\frac {v_{1}^{2}(r)}{r}},

Where  ~v_{1}(r) is the orbital rotation speed of the test body, which is directly proportional to the radius  ~r.

In view of (2) we find:

A=\int _{{0}}^{{R}}{\frac {GM(r)}{r}}\,dM=\int _{{0}}^{{R}}v_{1}^{2}(r)\,dM,

2C_{x}^{2}={\frac {A}{M}}={\frac {1}{M}}\int _{{0}}^{{R}}v_{1}^{2}(r)\,dM=\overline {v_{1}^{2}(r)},

C_{x}={\sqrt {{\frac {\overline {v_{1}^{2}(r)}}{2}}}}.

The speed  ~v_{1}(r) in its meaning is the first escape velocity as the orbital rotation speed on the current radius  ~r inside the ball. Then the characteristic speed  ~C_{x} of the ball in general is the square root of the squared first escape velocity, averaged over the volume of the ball, which is divided by  {\sqrt 2}.

If we take into account the escape velocities only on the ball’s surface with  ~r=R, then we can write for them:

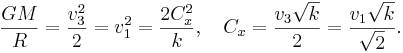
{\frac {GM}{R}}={\frac {v_{3}^{2}}{2}}=v_{1}^{2}={\frac {2C_{x}^{2}}{k}},\quad C_{x}={\frac {v_{3}{\sqrt k}}{2}}={\frac {v_{1}{\sqrt k}}{{\sqrt 2}}}.

Application

In the theory of  Infinite Hierarchical Nesting of Matter, the characteristic speeds of space objects’ particles fall into several distinct groups, corresponding to different classes. This allows us to almost definitely refer each object to one of the known classes according to the characteristic speed of its particles.

Partitioning of space objects into classes can be done with the help of the similarity coefficients, since between the objects there is similarity of matter levels, and for the stars there is discreteness of stellar parameters. If we assume that the coefficient of similarity in velocities is equal to  S_{0}=7.338\cdot 10^{{-4}}, then at the stellar level we have seven characteristic speeds for different classes of objects: [1]

1.    C_{1}=299792 km/s.

2.    C_{2}=70780 km/s.

3.    C_{3}=16710 km/s.

4.    C_{4}=3945 km/s.

5.    C_{5}=930 km/s.

6.    C_{6}=C_{s}=220 km/s.

7.    C_{7}=52 km/s.

The speed  C_{1} is equal to the speed of light, and it is assumed that this is the speed of the particles inside the proton, according to the substantial proton model, and of the particles within the hypothetical black holes.

In the speed range from  C_{3} to  C_{2} the  neutron stars are located, the range from  C_{5}  to  C_{4} includes white dwarfs, and the speeds of particles of the  main sequence  stars are greater than the stellar speed  C_{6}=C_{s}=220 km/s, but less than the speed C_{5}=930 km/s. The characteristic speeds of planets are not higher than  C_{7}=52 km/s, otherwise such a planet should be considered a stellar object.

For comparison, the characteristic speed of the Earth is 4.3 km/s, the characteristic speed of Jupiter is 23 km/s, the characteristic speed of the Sun is about 495 km/s.

The characteristic speed of a main sequence star can be expressed in terms of the stellar speed:  C_{m}=C_{s}(A/Z),

where  A and  Z are the mass and charge numbers, corresponding to the star from the point of view of similarity between atoms and stars. In turn, the stellar speed is determined through the speed of light and the coefficient of similarity in velocities:  C_{s}=cS_{0}. The stellar speed is one of the  stellar constants, and it determines the characteristic speed of particles of the main sequence star with minimum mass.

Large stellar systems, such as galaxies, consist of a number of stars, moving at quite high speeds around the common center of momentum of one or another system. Therefore, the characteristic speed for a galaxy is the average speed of the stars’ motion. For a large number of galaxies, there are dependences of the speed of the stars’ motion on the distance to the galactic center, which after averaging show the rotation of certain parts of the galaxy. If we average the speeds of the stars’ motion over the entire volume of the galaxy, the resulting average value will be proportional to the characteristic speed of this galaxy. This is the consequence of the virial theorem, according to which the absolute value of total energy of a system of particles is equal to kinetic energy of the particles.

Quantization of parameters of cosmic systems  is manifested at all levels of matter and it is a typical property of physical systems, which, after the exchange of energy (exchange of matter), return to their initial state. In this case, the characteristic speed of the system’s particles can again achieve the previous equilibrium value. Some physical systems with degenerate relativistic objects (atoms, neutron stars) achieve a large degree of discreteness and stability, so that their characteristic speeds change very little. It is known, for example, that the degree of accuracy of the best atomic clocks coincides with the accuracy of repetition of pulses, coming from pulsars.

In the space objects, the characteristic speed allows us to estimate the kinetic energy of the particles’ motion and the internal temperature. From the point of view of the Le Sage's theory of gravitation, gravitational energy of a body and gravitation force are created by fluxes of gravitons, penetrating all bodies. [2]  [3]   However, the fluxes of gravitons create not only the gravitational pressure, but also they transfer part of their energy to the particles, so that according to the virial theorem the internal kinetic (thermal) energy is not less than half of the absolute value of the body’s gravitational energy. Thus the interior of an equilibrium space body cannot get colder than a certain value, which depends on its mass and size, while maintaining the constant characteristic speed of the body’s particles. The same follows from solution of equations of the acceleration field for the relativistic uniform system, in which the Lorentz factor, the kinetic energy and the stationary velocity distribution of particles inside the body are determined.[4]  [5]

The speeds  C_{{x}} are boundary for the maximum rotation speeds of the stars’ surfaces, as well as for the average motion speeds of the stars relative to those stellar systems, in which these stars were formed (the principle of local stellar speed).

In Infinite Hierarchical Nesting of Matter, analogs of nucleons at the level of stars are neutron stars, and the characteristic speed of nucleons is higher than that of stars, approximately 4.3 times. The inverse of this quantity is the coefficient of similarity in speeds  S=0.23 between these levels of matter. If a neutron star consists of nucleons, then nucleons consist of similar particles of the lowest level of matter, called praons, and praons in turn consist of graons. Between the levels of nucleons and praons and between the levels of praons and graons, it is also possible to estimate the similarity coefficients for speeds, which turn out to be close to unity. This is due to the fact that nucleons inside a neutron star have a Lorentz factor of about 1.04, but the praons inside the nucleon and the graons inside the praon have a Lorentz factor of about 1.9.[6]

References

1.        Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999. ISBN 5-8131-0012-1.

2.        Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009). http://dx.doi.org/10.5281/zenodo.890886.

3.        Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.

4.        Fedosin S.G. The virial theore m and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8.

5.        Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x.

6.        Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.

External links

§   Characteristic speed in Russian

 

Source: http://sergf.ru/hsen.htm

On the list of pages