From Wikiversity

The extended special theory of relativity (ESTR) is the special theory of relativity (STR), derived in other axiomatics. The main difference of ESTR from STR is replacement of the postulate of the constancy of the speed of light and its independence on the motion of the sources of light and on the motion of the observer, by the postulate of the existence of an isotropic reference frame in which the speed of light is constant, depends neither on the direction of its propagation, nor on the velocity of the source of light. ESTR was developed by Sergey Fedosin in 2002 and is a special case of the metric theory of relativity. ^[1]

Contents 1 Works on the axiomatics of STR [1] 2 Introduction 3 Postulates of ESTR 4 Proof of equivalence of ESTR and STR 5 Results of ESTR 6 Substantiation of postulates 7 Other approaches 8 References 9 See also 10 External links

Works on the axiomatics of STR [1]

In 1910 at the meeting of German naturalists and doctors the Russian scientist Vladimir Ignatowski made a report "Some general remarks to the principle of relativity":^[2]

Now I raise a question for myself, what relations or, more precisely, equations of transformation we can arrive at, if we put in the top of the study only the principle of relativity.

Ignatowski showed that based on linear transformations, the principle of relativity and the isotropy of space we can derive the Lorentz transformations. In this derivation the second Einstein postulate of invariance of the speed of light was not used.

In the next 1911 year, in Annalen der Physik the work was published by Philipp Frank and Hermann Rothe: "On the transformation of the space-time coordinates from the fixed into the moving reference frames", ^[3] in which the approach of Ignatowski received significant development. Based on the group analysis, Frank and Rothe in the class of linear functions found the most general transformations between the inertial reference frames. They turned out depending on two fundamental constants with the dimension of velocity. Adding the axiom of space isotropy converts these transformations into the Lorentz transformations, and the axiom of time absoluteness – into the Galilean transformations. Frank and Rothe also were, apparently, the first who noted that the most general transformations between two inertial reference frames were the fractional-linear functions.

Despite the fundamental importance of these works for the questions of physics foundations, they remained practically unnoticed. Most of the educational literature up to the present time is based on the Einstein’s axiomatic approach. Among the few references to the works of Ignatowski, Frank and Rothe we can mention the textbook by Wolfgang Pauli "The Theory of Relativity." However, in connection with these works he wrote: ^[4]:

From the theoretic-group considerations we can obtain only the form of the transformation formulas but not their physical content.

This assumes that the fundamental speed constant, which occurs in the Lorentz transformations, can not be interpreted as the speed of light, without involving additional hypotheses.

We shall note that the idea, that in order to justify STR Einstein's second postulate is not required, has been repeatedly rediscovered, ^{[5] [6] [7] [8] [9]}, however, usually without reference to the fundamental works of 1910-1911 years. An overview of the works on the axiomatization of STR (in the framework of chronogeometry) can be found in the work by Gutz ^[10] in “Advances in Mathematical Sciences”. Among recent works there is the article Caligiuri and Sorli. ^[11]

The important difference of ESTR from the above works is that not only the axiom of space isotropy is used in it, but also the procedure of spacetime measurements by means of electromagnetic (or other) waves. This allows us to automatically determine the value of the theory’s constant, which has the dimension of speed, and to equate it to the speed of light (more precisely, to the speed of the corresponding wave).

Introduction

The analysis of the axioms and the results of SRT gives the following:

1. All inertial reference frames in STR are completely equivalent in the sense, that the kinematic characteristics of the physical processes in the moving frame are not identical but are similar to the characteristics of the same processes in the stationary reference frame. This means the Lorentz covariance of the mathematical form of physical laws.
2. All the effects of SRT in the final analysis are the consequence of the fact that the speed of light is limited.
3. The Lorentz transformations can be derived in different ways, in different axiomatics, including the use of representations of mathematical groups.

It is easy to see that the standard axiomatics of SRT is too rigid. It is extremely relativistic, bringing the principle of relativity of inertial reference frames to the absolute. From its postulates it is impossible to imagine the existence of at least one somehow preferred inertial frame. And the principle of independence of the speed of light is very ill-suited for the role of the basic axiom of STR. Indeed, the axiom as a rule is considered a statement which does not require proving due to its obviousness. But from the start the principle of independence of the speed of light on the observer's velocity was hard to understand and hardly agreed with the principle of relativity.

At the same time the true reason of constancy of the speed of light in the vacuum still remains unknown and the structure of the physical vacuum, in which electromagnetic waves propagate, is still a mystery. Are the light quanta independent autonomous objects with intrinsic wave properties, moving by inertia in the empty space, or do they transfer their energy and momentum through the oscillations of the vacuum medium by means of wave interaction? However that may be, the theory must be able to consider any effects of interaction of the vacuum as the medium with the electromagnetic field. The cross effects are also possible during the motion of bodies in the vacuum, when the electromagnetic wave is propagating inside these bodies, and the matter of bodies is interacting with the vacuum and changes the conditions of the motion of the waves. However, the standard axiomatics of STR does not allow considering these effects – for justification of STR the existence of the ether is not required, and therefore the properties of the ether or vacuum, as such, are not considered. Therefore in STR it is accepted not to speak about the possible effect of the vacuum on the properties of the moving bodies during the propagation of electromagnetic waves.

The purpose of development of the new axiomatics of STR was to eliminate the above drawbacks – to find the internally consistent, coherent theory axioms, to overcome the relativism absolutization, to expand the possibilities of the theory in describing the reality, while retaining all the previously achieved in STR results, repeatedly proven in practice. The result of this search was determining such postulate of the theory, which would replace the postulate of the constancy of the speed of light for all observers.

Postulates of ESTR

Both SRT and ESTR use the Poincare-Einstein principle of relativity and the electromagnetic waves for connection between the events in different inertial reference frames, provided that they take place in the vacuum or in the medium which does not affect the propagation of light. In both theories there are five axioms, that is, such basic assumptions which are accepted without proving. If in STR one of the basic axioms is the constancy of the speed of light and its independence on the motion of the light sources and on the motion of the observer, then in ESTR the axiom is used instead of it about the existence of the isotropic reference frame in which the speed of light is constant and does not depend on the direction of its propagation and on the velocity of the source of light.

The system of axioms of ESTR has the following form:

• 1) The principle of relativity holds (if all the material bodies of the physical system are brought to the state of free and uniform rectilinear motion relative to the frame, conventionally called the rest or stationary frame, then the phenomena in the moving reference frame for the co-moving observer would look as in the stationary reference frame for the fixed observer).
• 2) There is such an isotropic reference frame in which the speed of light propagation is equal in all directions and does not depend on the speed of the light emitter.
• 3) The validity of symmetries with respect to rotations in the Euclidean spacetime. In particular, during the motion of the reference frame the coordinate axes are considered to remain parallel to the axes of the fixed reference frame.
• 4) The validity of symmetries with respect to displacements in the Euclidean spacetime. This means the linearity of transformations of coordinates and time from one inertial frame to another (all the coordinates in the transformations are included in the first degree, the terms with higher degrees are absent). In addition it is assumed that the transverse length of the rod does not depend on the sign of the velocity of motion of the rod, and is determined by the magnitude of the velocity.
• 5) Spacetime measurements are carried out by means of electromagnetic or other waves propagating at high speed.

The measuring instruments can include electronic clock, measuring light grids, etc., which are the standards for ordinary mechanical rulers and clocks of any type. Synchronization of one clock with another is done by circulating of the wave taking into account the time of its delay at certain distance. In other words, the signal from the first clock should reach the second clock and come back, then the observer at the first clock will be able to give to the observer at the second clock the instruction to set the second clock with the time shift equal to half of the time of the signal’s way back and forth (the standard procedure of synchronization). Direct measurement of length is possible only in the stationary reference frame, and in case of motion of the object its length is determined indirectly by light signals sent from the ends of the object simultaneously to a stationary ruler.

Proof of equivalence of ESTR and STR

The logical scheme of ESTR is as follows. There is a fixed isotropic reference frame S₀ in the vacuum, in which the speed of light, by definition, is always equal to с. Then, we consider motion of reference frame S^’ at the constant velocity V₀ relative to S₀ along the axis OX (all the axes of the two frames are parallel to each other.) In S^’ the light is propagating at the speed с₁ against the axis OX and at the speed с₂ along the axis OX, and it is unknown beforehand whether these speeds are equal to each other. In S^’ one light detector is located at the origin of coordinates and two sources of light in different sides from the origin of coordinates. These sources of light are moving along the axis OX at some velocity V^’ relative to S^’. The periods are calculated of the waves which fall into the detector from the both light sources. After that, the situation is considered again in the frame S₀. By comparing the results, taking into account the recalculation of time intervals in different frames, we obtain two equations.

In the next step length of a body is calculated by means of calculating the time required for the light to move to the end of the body and back, in the fixed reference frame S₀ and in the moving reference frame S^’. Two quantities are introduced, one of which is equal to the ratio of the time readings, and the other is equal to the ratio of the measured lengths in both reference systems. The result is one more equation.

In the third step the system of the three obtained equations is solved. It is assumed that in each frame the observer carries out spacetime measurements by the same procedure. As a result, at first, the formula of speed addition of STR is obtained, the equality of speeds с₁ and с₂ to the speed of light с is proved, and a relation is derived for the recalculation of the Lorentz factor from one inertial frame to another. Based on the principle of relativity the effects of length contraction and time dilation are found. Thus, the formulas of STR and the postulate of constancy of the speed of light for all observers are derived in other axiomatics.

Results of ESTR

In order to understand difference between ESTR and STR, we shall consider propagation of light inside the moving bodies. In the reference frame S^’, where the body is at rest, the speeds of light inside the body с₃ and с₄ in the opposite directions of the axis OX depend on the absolute refractive index, and theoretically could also depend on the direction and the magnitude of the velocity of motion of the body in the isotropic reference frame S₀. This follows from the fact that motion of the body in S₀ can change the speed of light propagation inside the body, for example, similarly to the ether drag effect. From the point of view of S₀, the speeds of light inside the body will be equal to с₅ and с₆. From calculations we obtain relations between the directed in one way speeds с₄ and с₆, с₃ and с₅. These relations, in case of simplifying assumptions, turn into the standard formulas of speeds addition in the Fizeau experiment, when the moving water drags the light and effectively increases its speed.

But if no simplifications are made, ESTR implies the possibility of emergence of additional effects due to the inequality of the speeds с₃ and с₄. Such inequality of speeds is possible at high velocities or acceleration of the body in the isotropic frame. STR can not make similar predictions due to direct declaration of constancy of the speed of light in its axioms.

In contrast to STR, ESTR predicts the possibility of influence of properties of the physical vacuum, in which the material bodies are moving, on propagation of electromagnetic waves inside these material bodies. This influence is possible when the bodies are moving or being accelerated relative to the isotropic reference frame. Since the phase speed of light inside the material bodies depends on the absolute refractive index , then the influence of physical vacuum must be revealed through this index. In the theory of ESTR the transformations of the coordinates and time are as follows:

 

 

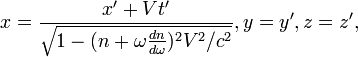
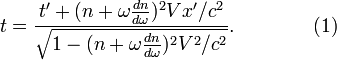
In the substance the refractive index depends on the angular frequency   of the wave according to the formula:

and the wave number    is also the function of    (where    is the wavelength). In the general case, in the Lorentz transformations instead of the speed of light propagation in the vacuum, we must substitute the group speed of light in the substance, which taking into account (2) equals:

This leads to transformations (1), different from the partial Lorentz transformations by introduction of the absolute refractive index  and its derivative with respect to the angular frequency of the wave  ,  in order to take into account the speed of the electromagnetic wave in the substance of any kind.

The absolute refractive index   in the general case depends not only on the properties of the substance, but also on the state of motion of this substance relative to the isotropic reference frame. Due to the influence of the physical vacuum, the measurements in the moving and accelerating bodies can lead to different results as compared with the external measurements of the time intervals and the lengths of the same bodies, and compared with the measurements inside of the bodies at rest in the isotropic reference frame. It must be taken into account also that in STR the measurements are commonly used which are external relative to the body, and in ESTR there is a possibility to carry out the spacetime measurements of the standards of length and time also by means of electromagnetic waves inside the material bodies.

The advantage of ESTR is that all the results of the special theory of relativity are derived based on more intuitively comprehensible system of axioms. In ESTR it is possible to carry out the spacetime measurements not only by means of electromagnetic, but also any other waves (e.g. gravitational), provided that the used standards of length and time will be constructed on the basis of these waves. ^[12] Accordingly, in all formulas the speed of light should be replaced by the propagation speed of the used wave. ESTR is the basis for the Lorentz-invariant theory of gravitation. In gravitational fields ESTR is replaced by the metric theory of relativity (MTR). ^[13] In ESTR it becomes possible to overcome the absolutization of relativity of the reference frames of STR, which is unacceptable from different points of view, including the philosophical point of view.

Special relativity is a special case with respect to the relativity in the curved spacetime. Just as in the general theory of relativity, in the covariant theory of gravitation the speed of electromagnetic signals near massive bodies changes under the action of gravitation and becomes less than the speed of light. In this case, the reference frame located at infinity from massive bodies can be considered as the preferred reference frame, so that in this reference frame the signal speed for space-time measurements will be equal to the speed of light. In this reference frame other special properties can be distinguished, such as isotropy, and the ESTR approach can be further applied.

The analysis of acceptable spacetime coordinate transformations based on the principle of general relativity applied to the inertial reference frames shows that the ether theories, in which there is an isotropic reference frame with the same speed of light in all directions, are subject to the Lorentz transformations for the physical quantities in the case of parallel motion of bodies or light signals. ^[14] Thus, the general theory of relativity, one of the particular cases of which is the special theory of relativity, does not prohibit the existence of the ether. ESTR uses the method of STR, by which for the maximum simplification of the procedure of measurements, the physical scales of length and time of real bodies, on the one hand, and the standards of their measurement based on the waves, on the other hand, are identified (after this the physical rulers and clocks are completely replaced by the wave standards of length and time). From this point of view ESTR is the simplest form of the theory of relativity, which includes STR and admits the existence of the ether or force vacuum field.

Substantiation of postulates

According to the logic of the axiomatic approach, there is no need to substantiate the axioms of the theory while the conclusions of the theory correspond to experiments and are proved in practice. However, in order to move over to a deeper level of scientific knowledge, the analysis of the essence and origin of axioms is required. This also applies to the axioms of the theory of relativity in all its forms, including STR, ESTR, the metric theory of relativity, etc. From this point of view it is possible to consider the force vacuum field, generating the gravitational and electromagnetic fields, which leads to interaction of the massive charged bodies in the framework of the mechanism of the Le Sage's theory of gravitation. ^{[15] [13] [16]} The specified vacuum field is the main content of the electrogravitational vacuum.

In the Infinite Hierarchical Nesting of Matter, the force vacuum field is a multicomponent field consisting of relativistic particles. Each basic level of matter generates its own component, which makes contribution to the vacuum field. Thus, it is assumed that the fluxes of praons generated by nucleons create the electromagnetic force ^[17] and the ordinary gravitation ^[18] as the force of attraction between macroscopic objects. In this case, the fluxes of relativistic praons are assumed to be similar in their properties to the cosmic ray fluxes, which arise mainly near neutron stars. In the chain “neutron star – nucleon – praon – graon”, each subsequent object is the main constituent of the previous object: if the neutron star consists of nucleons, then the nucleon consists of praons, and the praon consists of graons, etc. This chain can be continued not only in the direction of decreasing of the objects’ sizes, masses and energies, but also in the direction of increasing. All these objects, accelerated to relativistic velocities, are included into the force vacuum field and generate fundamental interactions at each level of matter. In addition, it can be argued that the photons, observed in standard experiments, also consist of praons, ^[19] whereas neutrinos are apparently composed of graons.

In view of the stated above, the postulates of the STR that the speed of light depends neither on the velocity of the light source, nor on the velocity of the observer or the receiver of the light signal, can be understood in the following way. At the moment of a photon formation in the light source, the fluxes of praons, moving at almost the speed of light and having a very large Lorentz factor, pass through the excited atom and are modulated by its electromagnetic field, that is, the field of the nucleus and excited electrons. This leads to formation of a rigid periodic structure of the emerging photon, in which praons are held near each other by the strong gravitation. When a photon is formed, its linear velocity almost does not differ from the average velocity of the fluxes of praons, the only difference is that the praons inside the photon get additional rotation under the action of the atom’s field. It is the rotational energy of the photon’s particles and energy of its electromagnetic field that is fixed by the light receiver, leading to excitation of electrons, while the energy of motion of the photon as a whole is not determined in the experiment.

If the light source is moving relative to the isotropic reference frame, this does not influence the speed of the praons’ fluxes and the speed of the emerging photons. It’s only the photon’s periodic structure and the corresponding length of their waves that changes, which is equivalent to the red or blue shift of the photons’ frequency, depending on the direction of the velocity of the light source relative to the stationary light receiver. This allows us to explain the Doppler effect due to the motion of the light source and the independence of the speed of light from the motion of the light source.

In the opposite situation, the light source is stationary, and the receiver is moving relative to the isotropic reference frame, and therefore it detects the Doppler effect as a change in the frequency in each of the photons reaching the receiver. In fact, the wavelength of the photon, as the distance between two adjacent wave crests inside the photon, does not change at all. If we multiply this constant wavelength by the wave frequency in the moving receiver, we will obtain the wave velocity that is not equal to the speed of light. However, according to the postulate of STR, the speed of light does not depend on the velocity of the receiver. This leads to the paradox of STR about contraction of the sizes of moving bodies (Lorentz contraction), including the wavelength of the photon reaching the receiver. In the ESTR, according to the fifth postulate, all measurements are made with the help of the light signals and using the same procedure. In this case, agreement between the results of the same-type measurements in different inertial reference frames is achieved only in the case when the speed of light is assumed to be constant in all reference frames. From this it is clear that the main task of STR is not the description of events from the point of view of physics, but the mathematically correct interpretation of the results of relativistic experiments, regardless of the paradoxes that arise. The role of the ESTR reduces to explaining this from other perspectives than in the STR, based on a more understandable system of axioms.

 

Other approaches

The theoretical approach developed by Robertson, Mansouri and Sexl (the references are provided in the article Robertson–Mansouri–Sexl framework) is close enough to ESTR. This approach suggests the possibility of existence of a preferred (privileged) reference frame as a reference frame with special properties (see the article preferred frame) and is used as a basis for verifying the conclusions of the special theory of relativity. Robertson also considered isotropic reference frames, in which the speed of light is the same in all directions.

A. M. Chepick called isotropic reference frames “absolute reference frames” and analyzed transformations of coordinates and time between the moving inertial reference frames and absolute reference frames. ^[20] In this case he used an additional postulate: ^[21] “In any inertial reference frame in the vacuum, the time of motion of the light signal along the closed linear contour does not depend on the position of this contour.” This led him to the STR formulas, including the Lorentz transformations.

 

References

1. Fedosin S.G. Sovremennye problemy fiziki: v poiskakh novykh printsipov, Moscow: Editorial URSS, 2002, 192 pages. ISBN 5-8360-0435-8.
2. von W. v. Ignatowsky, «Einige allgemeine Bemerkungen zum Relativitätsprinzip», Verh. d. Deutsch. Phys. Ges. 12, 788-96, 1910 (русский перевод)
3. von Philipp Frank und Hermann Rothe «Über die Transformation der Raumzeitkoordinaten von ruhenden auf bewegte Systeme», Ann. der Physik, Ser. 4, Vol. 34, No. 5, 1911, pp. 825—855.
4. Pauli, Wolfgang (1981). Theory of Relativity. New York: Dover Publications. ISBN 0-486-64152-X.
5. Терлецкий Я. П. — Парадоксы теории относительности, М.: Наука (1965)
6. Mermin N.D. — «Relativity without light», Am.J.Phys., Vol. 52, No. 2 (1984) p. 119—124. Русский перевод: Мермин Н. Д. — «Теория относительности без постулата о постоянстве скорости света», Физика за рубежем. Серия Б. (1986)
7. Lee A.R. Kalotas T.M. — «Lorentz transformations from the first postulate», Am.J.Phys., Vol. 43, No. 5, (1975) p. 434—437.
8. Achin Sen «How Galileo could have derived the special theory of relativity» Am.J.Phys., Vol. 62, No. 2 (1994) p. 157—162.
9. Nishikawa S. — «Lorentz transformation without the direct use of Einstein’s postulates» Nuovo Cimento, Vol. 112B, No. 8 (1997) p. 1175—1187.
10. А. К. Гуц, «Аксиоматическая теория относительности», УМН, 37:2(224) (1982), с. 39—79.
11. Luigi Maxmilian Caligiuri, Amrit Sorli, Special Theory of Relativity Postulated on Homogeneity of Space and Time and on Relativity Principle, American Journal of Modern Physics. Vol. 2, No. 6, pp. 375-382 (2013).
12. Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron, Vol. 14, No. 4, pp. 385-413 (2007). http://dx.doi.org/10.5281/zenodo.891124.
13. ^{13.0 13.1} Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. Perm, 2009-2011, 858 pages, Tabl. 21, Pic. 41, Ref. 293. ISBN 978-5-9901951-1-0. (in Russian).
14. Alexander L. Kholmetskii. Empty space-time, general relativity principle and covariant ether theories. 12 Jan 2005. arXiv:physics/0501060v1.
15. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009). http://dx.doi.org/10.5281/zenodo.890886.
16. Fedosin S.G. The Force Vacuum Field as an Alternative to the Ether and Quantum Vacuum. WSEAS Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN: 1991‒8747 / 2224‒3429, Volume 10, Art. #3, pp. 31-38 (2015). http://dx.doi.org/10.5281/zenodo.888979.
17. Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.
18. Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348‒0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
19. Fedosin S.G. The substantial model of the photon. Journal of Fundamental and Applied Sciences, Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.
20. Chepick A.M. Absolute. Main principles. Modern problems of statistical physics, Vol. 6, pp. 111-134 (2007). Published in NNGU; на русском языке: Абсолют. Основные принципы. Актуальные проблемы статистической радиофизики, т.6, с.111-134 (2007).
21. Обухов Ю.А., Захарченко И.И. Светоносный эфир и нарушение принципа относительности. Физическая мысль России, №3, 2001, Москва, МГУ им. М.В. Ломоносова.

See also

• Special relativity
• Metric theory of relativity
• General relativity
• Lorentz-invariant theory of gravitation

External links

• Extended special theory of relativity in Russian

 

 

 

Source: http://sergf.ru/rsten.htm

On the list of pages