На русском языке

Praon

Praons is the general name for a family of hypothetical particles, consisting of neutral n-praons and positively charged p-praons. In the theory of Infinite Hierarchical Nesting of Matter, praons are similar in their properties to nucleons, that is, to neutrons and protons. To assess the properties of praons, the similarity of matter levels is used. It is assumed that praons consist of graons in a similar way as nucleons consist of praons, and neutron stars consist of nucleons. Ultrarelativistic flows of praons are one of the components of the electrogravitational vacuum, which, along with the streams of graons, are responsible for the occurrence of gravity and electromagnetic interaction. ^[1]

Содержание

1 Origin
2 Properties
3 Wave quanta
4 See also
5 References
6 External links

Origin

Supposing that SPФ symmetry is valid at all levels of matter, the laws of nature act in the same way at these levels. Hence we can assume that as nucleons form the ordinary matter, so praons are the basis of the matter from which nucleons, electrons and other particles are composed. A typical neutron star contains approximately Ф = 1.62∙10⁵⁷nucleons, and the same number of praons is expected inside each nucleon. This allows us to understand why in accelerators in collisions of nucleons with particles of the highest energy, decay products behave like liquid plasma jets, and no fairly large particles, such as partons or individual quarks, are detected. It is assumed that 61% of all praons in the Universe are part of nucleons, and 39% form dark matter, including part of nuons. ^[2]

In general, we can talk about the wave of matter evolution in the Universe. A typical scenario for the appearance of a neutron star is as follows: first, under the action of gravitation compression of a large gas cloud takes place, in which the primary stars emerge. The evolution of a star of sufficient mass ends with a supernova and birth of a neutron star, and the evolution of the low-mass stars turn into white dwarfs. Thus, before the appearance of compact star remnants, there must have been the matter in the form of gas. Similarly, we can imagine that the existence of the matter of praons in the form of gas eventually led to the formation of the matter of nucleons such as hydrogen gas clouds. The wave of evolution in this case moves in the direction from the lower levels of matter to the higher levels of matter, from the smallest particles, such as graons, to praons, then to nucleons, neutron stars and to even larger objects. Since each basic level of matter generates its own fluxes of relativistic particles and wave quanta that generate fundamental interactions, such as gravitation and electromagnetism based on the mechanism of Le Sage’s gravitation, then the wave of evolution also refers to fundamental interactions. This means that emergence of objects of a certain level of matter would be impossible if there would be no sufficiently large number of particles of the lower levels of matter and no fluxes of relativistic particles, generated by them and making their contribution into the multicomponent vacuum force field.

Properties

A typical neutron star has the mass of 1.35 Solar masses, the radius of the order of 12 km, and the characteristic speed of particles in such a star reaches 0.23 of the speed of light. Dividing these values by the corresponding values for the proton, we obtain the similarity coefficients: in mass Ф = 1.62∙10⁵⁷, in sizes Р = 1.4∙10¹⁹, and in speed S = 2.3∙10^{– 1}. In the first approximation, we can assume that the same similarity coefficients in mass and sizes are also valid for the relationship between praons and nucleons. Hence we determine the praon mass $~m_{{pr}}=1\cdot 10^{{-84}}$ kg and its radius $~r_{{pr}}=6.2\cdot 10^{{-35}}$ m, in this case we used the proton radius $~r_{{p}}=8.73\cdot 10^{{-16}}$ m. ^[3] Using the mass and radius of the praon we can estimate the average density of its matter $~\rho _{{pr}}=1\cdot 10^{{18}}$ kg /m³.

The characteristic speed for the particles of matter inside the proton and praon is close enough to the speed of light. In this case, instead of the particles’ speed it is convenient to use their Lorentz factor. In the relativistic uniform model, there is a formula for the dependence of the Lorentz factor on the current radius inside the system of particles of a spherical shape, held in equilibrium by the gravitation force and the force of internal pressure: ^[4]

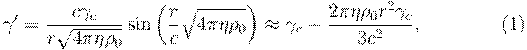
$~\gamma '={\frac {c\gamma _{c}}{r{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\approx \gamma _{c}-{\frac {2\pi \eta \rho _{0}r^{2}\gamma _{c}}{3c^{2}}},\qquad \qquad (1)$

where is the speed of light, $~\gamma _{c}$ is the Lorentz factor of the particles at the center of the sphere, is the current radius, $~\rho _{0}$ is the invariant mass density of the system’s particles, $~\eta$ is the coefficient of the acceleration field.

In such objects as the neutron star, proton, and also praon, the average mass density does not differ much from the central mass density, so that this formula must provide the correct order of magnitude of the Lorentz factor. We will now use the expression for the rest mass of a spherical body:

$~m_{b}={\frac {c^{2}\gamma _{c}}{\eta }}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right].\qquad \qquad (2)$

If we substitute here the neutron star’s mass instead of $~m_{b}$ , the star’s radius instead of , and use the average mass density instead of $~\rho _{0}$ , and also take into account the equality $~\eta \approx {\frac {3G}{5}}$ , ^[5] where is the gravitational constant, then we can calculate the Lorentz factor for the nucleons at the center of the star: $~\gamma _{c}=1.04$ . The similar approach can be applied to the proton, with the difference that instead of the ordinary gravitational constant we should use the strong gravitational constant $G_{a}=1.514\cdot 10^{{29}}$ m³•s^–2•kg^–1. So it turns out that at the center of the proton the Lorentz factor for the praons, located there, equals 1.9. ^[6]

Finally, for the praon it is necessary to use the gravitational constant $~G_{{pr}}$ , acting at its level of matter.

To estimate this constant, we can apply the similarity relations between the levels of praons and nucleons: $~{\frac {G_{a}}{G_{{pr}}}}={\frac {PS^{2}}{\Phi }}$ . Hence it follows that the value of the praon’s gravitational constant is $~G_{{pr}}=3.3\cdot 10^{{68}}$ m³•s^–2•kg^–1. After substituting into (2) the mass, radius and density of the praon, taking into account the equality $~\eta \approx {\frac {3G_{{pr}}}{5}}$ , we find the Lorentz factor for graons at the center of the praon, which is approximately equal to 64.

The typical angular momentum at each level of matter is given by the Dirac constant. For compact stars $~\hbar _{s}=\hbar \Phi PS=5.5\cdot 10^{{41}}$ J∙s, for the nucleons’ level of matter $~\hbar =1.054\cdot 10^{{-34}}$ J∙s, while the quantum spin of the nucleon is equal to $~\hbar /2$ . To estimate the Dirac constant $~\hbar _{{pr}}$ at the level of praons, the following similarity relation can be used: $~{\frac {\hbar }{\hbar _{{pr}}}}=\Phi PS$ . Hence it turns out that $~\hbar _{{pr}}=2\cdot 10^{{-110}}$ J∙s.

The Boltzmann constant for the level of praons is given by the expression: $~k_{{pr}}={\frac {k}{\Phi S^{2}}}=1.6\cdot 10^{{-79}}$ J/K, where is the Boltzmann constant.

For the strong gravitational constant the following relation holds true:

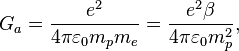
$G_{a}={\frac {e^{2}}{4\pi \varepsilon _{{0}}m_{p}m_{e}}}={\frac {e^{2}\beta }{4\pi \varepsilon _{{0}}m_{p}^{2}}},$

Where is the elementary charge, $~\varepsilon _{{0}}$ is the electric constant, $~m_{p}$ is the proton mass, $~m_{e}$ is the electron mass, $~\beta ={\frac {m_{p}}{m_{e}}}=1836.152$ is the ratio of the proton mass to the electron mass. Similarly, at the level of praons we obtain the following:

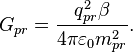
$G_{{pr}}={\frac {q_{{pr}}^{2}\beta }{4\pi \varepsilon _{{0}}m_{{pr}}^{2}}}.$

Hence we find the praon’s charge $~q_{{pr}}=4.6\cdot 10^{{-57}}$ C. If we use the theory of similarity, then the charge of the praon is expressed through the charge of the proton (elementary charge) and the coefficients of similarity as follows: $~q_{{pr}}={\frac {e}{S{\sqrt {\Phi P}}}}=4.6\cdot 10^{{-57}}$ C .

By analogy with a free neutron, which undergoes beta-decay in $~t_{n}=880.1$ seconds, we can estimate the lifetime $~t_{{pr}}$ of a free neutral n-praon. To do this, we can use the similarity relation $~{\frac {t_{n}}{t_{{pr}}}}={\frac {P}{S}}$ , which gives $~t_{{pr}}=1.4\cdot 10^{{-17}}$ seconds.

Wave quanta

It is assumed that praons are not only “the building material” for nucleons and electrons that form the matter, but also they make up the composition of all hadrons and leptons. Moreover, such wave quanta as photons should also consist of praons. During transition of the excited electron in the atom to the state with lower energy, the center of the electron cloud is shifted relative to the nucleus, which leads to the quantum spin of the electron (see substantial electron model). In this case, the periodic electromagnetic field of the rotating electron appears, acting on the fluxes of the vacuum field’s praons and making up a photon of them. In the substantial photon model, praons are closely associated with the strong gravitation and form sufficiently rigid wave structure of the photon, rotating during its motion. ^[7] For the case of the electron transition from the second level to the first level in the hydrogen atom, when a photon with the angular frequency $~\omega =1.54946\cdot 10^{{16}}$ s ^-1is emitted in the Lyman series, the total rest mass of all the praons of such a photon is equal to $~m_{{ph}}=1.6\cdot 10^{{-42}}$ kg. If we divide the mass $~m_{{ph}}$ by the rest mass of one praon $~m_{{pr}}=1\cdot 10^{{-84}}$ kg, we can estimate the number of praons in this photon: $~N_{{ph}}=1.6\cdot 10^{{42}}$ .

Let us now consider the electron antineutrino emitted in the free neutron decay. If from the energy of the neutron at rest we subtract the rest energy of the proton and the electron, arising from the decay, then the energy obtained will be equal to the antineutrino energy, to which we must add the sum of the kinetic energies of the electron and the proton. In the limiting case, the sum of the kinetic energies of the electron and the proton is minimal, and the antineutrino energy reaches the maximum possible value of $~E_{{an}}=782.318$ keV or $~1.253412\cdot 10^{{-13}}$ J. If we denote by $~m_{{an}}$ the total rest mass of all the particles making up the antineutrino, then for the antineutrino energy we can write: $~E_{{an}}=\gamma m_{{an}}c^{2}$ , where is the speed of light. Hence, with the Lorentz factor equal to $~\gamma =1.9\cdot 10^{{11}}$ , as in the case of the photon, we can estimate the antineutrino mass: $~m_{{an}}=7.3\cdot 10^{{-42}}$ kg. It turns out that the mass of all the particles of this antineutrino is 4.6 times greater than the mass of praons in the photon, emitted in the hydrogen atom at the angular frequency $~\omega =1,54946\cdot 10^{{16}}$ s^-1in the Lyman series.

According to the substantial neutron model, the electron antineutrino, emitted from the neutron in its beta decay, is made of the praantineutrinos and praneutrinos, which arise respectively in the beta decay of n-praons, that compose the neutron, and in the capture of praelectrons by p-praons, that is, in the weak interaction reactions, but already at the level of matter of praons. ^[^8] This means that the electron antineutrino consists of multiple parallel fluxes of the vacuum field’s graons, while each of these fluxes is formed at the moment when the corresponding neutron’s praon is transformed in the weak interaction reaction. The parallel alignment of the graon fluxes is due to the fact that the magnetic moments of the praons inside the neutron are directed by the strong magnetic field of the neutron. Antineutrino by its form represents a cylindrical object moving at the speed of light, with the cross-section equal to the cross-section of the neutron. The right helicity of antineutrinos means that the graon fluxes are twisted to the right relative to the direction of motion of antineutrinos, which coincides with the spin direction of the decaying neutron. The stability of antineutrinos is maintained by the strong gravitation acting at the level of graons and by electromagnetic forces.

It is assumed that the emission time of an antineutrino during the decay of a free neutron should be comparable with the lifetime of free n-praons $~t_{{pr}}=1.4\cdot 10^{{-17}}$ seconds.

For comparison, we can consider the formation of a neutron star in a supernova, which occurs with the emission of neutrino and antineutrino fluxes with a total duration of the order of $~t_{s}=10$ seconds. At the level of the matter of nucleons, such a process can be considered as the formation of a neutron, with the emission of fluxes of praantineutrinos and praneutrinos. The radiation time is estimated as $~{\frac {t_{s}S}{P}}=1.6\cdot 10^{{-19}}$ seconds at .

From this we see that the structures of the photon and the antineutrino are absolutely different, they also differ in the composition of their main particles. Being composed of the smallest graons, neutrinos and antineutrinos have an extremely high penetrating ability, in spite of the fact that they have energies and rest masses comparable with those of photons.

See also

References

1. Fedosin S.G. On the structure of the force field in electro gravitational vacuum. Canadian Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp. 5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206.

2. Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp. 3-13 (2012). http://dx.doi.org/10.5281/zenodo.890806.

3. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451.

4. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12.

5. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.

6. Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.

7. Fedosin S.G. The substantial model of the photon. Journal of Fundamental and Applied Sciences, Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.

8. Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).

External links

Praon in Russian

Source: http://sergf.ru/praen.htm

On the list of pages