На русском языке

Nuon

Nuon is a hypothetical neutral particle, which has the properties of a muon, but it differs from it by its origin. Nuon as a necessary new particle first appeared in the theory of Infinite Hierarchical Nesting of Matter in 2009 in the course of explanation of the evolution of elementary particles. [1] From the standpoint of similarity of matter levels and SPФ symmetry, the nuon’s analogue at the level of stars is a white dwarf.

Contents

  • 1 Origin
  • 2 Properties
  • 3 Muon
  • 4 Influence on cosmological model
  • 5 See also
  • 6 References
  • 7 External links

Origin

In the theory of infinite nesting of matter it is assumed that evolution of the main levels of matter, which include the level of elementary particles and the level of stars, occurs by the same laws. Hence, it follows that the well-developed theory of stellar evolution with necessary amendments can be used to describe the origin and evolution of elementary particles. The similarity of matter levels leads to the conclusion that at the level of stars neutrons correspond to neutron stars, protons correspond to magnetars, and electrons correspond to discons or disks, discovered near neutron stars. [2] Similarly, the analogues of pions are neutron stars of lowest possible mass, and the analogues of muons are white dwarfs, which remain after the decay of low mass neutron stars. White dwarfs arise from the main sequence stars in the course of natural evolution, at the end of the stage of thermonuclear fuel burn-up (hydrogen, helium, carbon, etc.) in the interior of stars. This white dwarf represents the bare core of a star at the red giant stage, which has blown off its outer envelope, which forms a planetary nebula.

In sufficiently massive stars the stage of thermonuclear burning reaches fusion of light atoms into the iron atoms, and in the stellar core much iron is accumulated. Due to further increase of the internal pressure, matter neutronization takes place by means of capture of electrons by atomic nuclei, so that the stellar core becomes unstable. This results in a supernova with a collapse of the stellar core, formation of a neutron star, discharge of the envelope due to the conversion of gravitational energy into kinetic energy and rebound of the envelope from the formed neutron star. A neutron star can also be formed when the mass of the carbon-oxygen white dwarf exceeds the mass limit (the Chandrasekhar limit).

The described scenario can be applied to the level of elementary particles. This means that even before appearance of electrons and nucleons, in our Universe there must have existed (and periodically reappear) objects similar in their properties to planets and main sequence stars, but with the size and mass typical for the level of elementary particles. It is assumed that the main force that kept those objects from decay was strong gravitation. Evolution of those objects leads to emerging of electrons, nuons and nucleons.

Properties

To estimate the mass and radius of nuons we must use the coefficients of similarity between the matter levels: in mass  Ф = 1.62∙1057 , in size  Р = 1.4∙1019 , in velocity  S = 2.3∙10-1 . The masses of the observable white dwarfs range from 0.17 to 1.33 Ms , and the mass of the majority of them is about 0.6 Ms , where  Ms  denotes the Solar mass. Dividing the masses by  Ф , we obtain the mass range for nuons: from 2.1•10-28 kg up to 1.63•10-27 kg, which is slightly less than the proton mass, equal to 1.6726•10-27 kg.

The radii of white dwarfs decrease with increasing of their mass and range from 0.008 to 0.02 Rs , where  Rs  is the Solar radius. If we divide these radii by the coefficient of similarity in size  Р , we can estimate the range of nuons’ radii: from 3.98•10-13 m to 9.94•10-13 m.

The white dwarf with the mass 0.6 Ms has the radius of about 0.0138 Rs . [3] The nuon corresponding to it has the mass  m=7.36 \cdot 10^{-28} kg and the radius  r = 6.86 \cdot 10^{-13} m. Using the mass and radius we can determine the characteristic speed of particles inside this nuon:

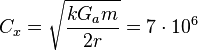C_x = \sqrt { \frac {k G_a m }{2r} } = 7 \cdot 10^{6}m/s,

where  G_a = \frac{e^2}{4 \pi \varepsilon_{0} m_p m_e } = 1.514 \cdot 10^{29} m 3• s –2• kg–1  is the strong gravitational constant, ~e   is the elementary charge, ~\varepsilon_{0}   is the electric constant, ~ m_p   is the proton mass, ~ m_e   is the electron mass, ~ k=0.6   is for a uniform ball and increases when the density in the center of the ball is higher than the average density.

To estimate the characteristic spin angular momentum of the nuon we use an approximate formula: [4]

L_s = \frac {m C_x r }{4 \pi} = 2.8 \cdot 10^{-34} J•s.

The characteristic angular momentum of the nuon under consideration exceeds the quantum spin of the proton, which is equal:

\frac {h }{4 \pi}= \frac {\hbar }{2} = 5.27 \cdot 10^{-35} J•s,

here ~ h   is the Planck constant, ~ \hbar   is the Dirac constant.

The next level after the level of elementary particles is the level of praons, which correlate with nucleons just as nucleons correlate with neutron stars. [1] In white dwarfs, the nucleons are bound in atomic nuclei, however the atoms are almost entirely in the ionization state, and the mixture of nuclei and electrons creates the matter in the form of plasma. The same holds true for the nuons’ state of matter, which must consist of positively charged praons and negatively charged particles – the analogues of electrons (praelectrons).

The pressure and temperature in the center of the nuon are estimated by the formulas: [5]

p_c = \frac {3 \sigma_a m^2 }{8 \pi r^4}= \frac {9 G_a m^2 }{8 \pi r^4}= 1.3 \cdot 10^{23} Pa,

 

T_c = \frac {\eta_a m m_{pr} }{3 k_{pr} r}= \frac {G_a m m_{pr} }{k_{pr} r }= 1 \cdot 10^{9} K,

where ~ \sigma_a   is the pressure field coefficient, ~ \eta_a   is the acceleration field coefficient, ~ m_{pr} = \frac {m_p}{\Phi} = 1 \cdot 10^{-84} kg is the praon mass, ~ k_{pr} = \frac {k}{\Phi S^2} = 1.6 \cdot 10^{-79} J/K is the Boltzmann constant for the level of praons, ~ k  is the Boltzmann constant.

The concentration of praons in the center of the nuon is:

n_c = \frac {p_c }{k_{pr} T_c }= 8 \cdot 10^{92} m-3 .

For the concentration of praons and the mass density averaged over the nuon’s volume we can write the following:

n = \frac {3 m }{ 4 \pi m_{pr} r^3}= 5.4 \cdot 10^{92} m-3 .

 

\rho = n m_{pr} = 5.4 \cdot 10^{8} kg/m3 .

The Chandrasekhar limit indicates the maximum mass of a white dwarf, beyond which a white dwarf can become a neutron star. This mass depends on the chemical composition and ranges from 1.38 Ms to 1.44 Ms . Dividing this mass by the coefficient of similarity in mass  Ф , we can estimate the maximum mass of a nuon, which is ready to turn into a neutron: 1.767•10-27 kg. For comparison, the neutron mass is 1.675•10-27 kg.

Being a neutral particle, a nuon can hardly be identified in the experiments. However, muons as charged nuons are accessible enough and a number of researches are carried out with them.

Muon

The main thing, in which a nuon differs from a muon, is that a nuon is neutral and a muon has a charge, since it is formed from the charged pion.

Strong gravitation allows maintaining the spherical shape of a muon despite the fact that it bears the elementary charge  ~ e . From the ratio of the gravitational and electrical forces acting on the matter unit with the mass ~ \Delta m   and the charge ~ \Delta e   on the muon’s surface we can see that the following inequality holds:

\frac { G_a m_\mu \Delta m }{r^2}> \frac {e \Delta e }{4 \pi \varepsilon_0 r^2}, \quad m^2_\mu > m_p m_e,

provided that  \frac { \Delta m }{\Delta e }= \frac { m_\mu }{ e },  and with regard to the definition of the strong gravitational constant  ~ G_a .

A muon is a charged nuon of the lowest possible mass, which equals  m _{\mu}= 1.88 \cdot 10^{-28} kg; at such mass the muon’s matter becomes unstable – on the average in  t _{\mu}= 2.197 \cdot 10^{-6} seconds the muon decays into an electron, a muon neutrino and an electron antineutrino. At the level of stars it looks as if a charged ultralight white dwarf with the mass  ~M _{wd}= m _{\mu} {\Phi} =0.15 M_s   in a time up to  t _{wd}= \frac {t _{\mu} P}{S} = 4.2   million years collapsed with emission and formation of a negatively charged object of low density. This time can be associated with the cooling time of a white dwarf, after which recombination of matter ions and electrons, the pressure drop in the star interior and transformation of the matter phase state from ion-electron plasma to hot partially ionized atomic gas with an increase in the star volume take place. The gas shell of the star as a whole due to ordinary gravitation is not able to keep any significant electric charge, and the charged matter is discharged from the star. At the same time, a charged white dwarf or a neutron star can retain the stellar charge of the value  ~ Q_s = e (\Phi P)^{0,5} S = 5.5 \cdot 10^{18} C, since the electrons are held in atoms and ions by electrical forces, and the matter’s atoms and nucleons are held together by strong gravitation in addition to ordinary gravitation.

According to theoretical calculations, a white dwarf with the mass  ~M _{wd}= 0.15 M_s   must have a radius of the order of ~R _{wd}= 0.022 R_s . Dividing this value by the coefficient of similarity in size  Р , we can estimate the radius of a muon and its density:

r _{\mu} = 1.09 \cdot 10^{-12} m,

 

\rho_{\mu} = \frac {3 m _{\mu} }{ 4 \pi r^3_{\mu} }= 3.5 \cdot 10^{7} kg/m3 .

Near the proton the muon should decay under the action of strong gravitation and form a disk around the proton similar to the electron’s disk according to the substantial electron model. The proton mass density  \rho_p = \frac {3 m _p }{ 4 \pi r^3_p }= 6 \cdot 10^{17} kg/m3 substantially exceeds the muon density, here the value r_p = 8.73 \cdot 10^{-16} m is taken as the proton radius. [6] The Roche limit, at which the muon must decay near the proton, is given by a formula:

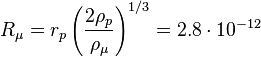R _{\mu} = r_p \left( \frac {2 \rho_p }{\rho_{\mu} }\right)^{1/3} = 2.8 \cdot 10^{-12} m.

As a result, the muon disk is located much closer to the nucleus than the electron disk in the hydrogen atom, for which the characteristic radius is the Bohr radius  a _B = 5.29 \cdot 10^{-11} m as the Roche limit corresponding to the electron.

Influence on cosmological model

In the observed galaxies, the number of white dwarfs is less than 10% of all stars and the number of neutron stars is about 10-100 times less than white dwarfs. Long-lasting evolution of stellar systems, taking into account decrease in the number of white dwarfs due to collisions with neutron stars, can lead to the fact that in the distant future a large number of white dwarfs can remain in the Metagalaxy, which is comparable to the amount of neutron stars. If we apply this pattern to the level of elementary particles, it is expected that in addition to the matter in the form of atoms and electrons there should be a significant proportion of nuons in space, which are the analogues of white dwarfs.

Using the coefficients of similarity we can calculate the ratio of the average density of nucleon matter in the Metagalaxy to the total density of praon matter, which is equal to 0.61. [7] The nucleons consist of praons, and it turns out that some portion of the praon matter is not part of nucleons. Approximately 39% of the entire mass should have a different form, in particular, the form of nuons. As a result, we can consider nuons as good candidates for the role of neutral particles of dark matter that have no charge and manifest themselves through gravitational effects.

Besides, nuons are significantly larger in size than nucleons, which allows us to suggest a new hypothesis of the tired light to explain the effect of cosmological redshift. The essence of the hypothesis is that the light is scattered on the medium’s particles according to the Beer–Lambert–Bouguer law and loses its energy. If it is considered true for each individual photon, then we can write for the exponential energy attenuation of the photon the following:

~W = W_0 \exp (\sigma n d),

 

~W = W_0 \exp (H d/c),

where ~ W_0   is the photon energy when it emerges, ~ \sigma   denotes the cross-section of the photons’ interaction with nuons, which is equal by the order of magnitude to the nuon’s cross-section, ~ n   is the average concentration of nuons in cosmic space, ~ d   is the path traveled by the photon, ~ H  is the Hubble constant, ~c   is the speed of light.

Hence we obtain the relation of the form ~ H = \sigma n c . If the redshift effect is caused by the interaction of photons with nuons, then the redshift can be irregular in different directions in the sky, as a consequence of different average concentration of nuons on the way of photons. This effect is really observed, leading to almost two times different values of the Hubble constant in calculations of researchers studying different areas of the sky. The scattering of photons on nuons also allows us to explain the observed change in the number of photons from distant supernovae, which is expressed in the fact that these supernovae seem to be located 10-15% farther than they actually are, and their stellar magnitudes at maximum brightness differ from the magnitudes of close supernovae. In addition, nuons can thermalize the stellar emission converting it into the observed relic radiation and acting as a global blackbody. These properties of nuons call in question the Big Bang model.

See also

References

  1. 1.0 1.1 Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
  2. Wang Zhongxiang, Chakrabarty Deepto, Kaplan David L. A Debris Disk Around An Isolated Young Neutron Star. arXiv: astro-ph / 0604076 v1, 4 Apr 2006.
  3. M.A. Barstow, H. E. Bond, M.R. Burleigh, S.L. Casewell, J. Farihi, J.B. Holberg, I. Hubeny. Refining our knowledge of the white dwarf mass-radius relation. Eds Patrick Dufour. Proceedings of the 19th European White Dwarf Workshop, Montreal, 11-15 August, 2014.
  4. Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999, ISBN 5-8131-0012-1, Tab. 66. Fig. 93. Ref. 377 titles. (In Russian).
  5. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12 .
  6. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012).
  7. Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp. 3-13 (2012).

External links

Source: http://sergf.ru/nuen.htm

On the list of pages