На русском языке

Substantial proton model

The substantial proton model describes the origin, structure, state of matter, and other properties of the proton based on the idea of two fundamental force fields, acting in the nature. According to the theory of Infinite Hierarchical Nesting of Matter, these fields include the electromagnetic field and gravitational field. In the presented model, the de Broglie wavelength of moving protons is explained as a consequence of conversion of the wavelength of internal oscillations of potentials of the fundamental fields of these particles into the laboratory reference frame.

Contents

  • 1 The magnetic moment
  • 2 The radius
  • 3 The state of matter
  • 4 Composite objects
  • 5 The nucleon annihilation
  • 6 The reactions of weak interaction
  • 7 The origin
  • 8 References
  • 9 See also
  • 10 External links

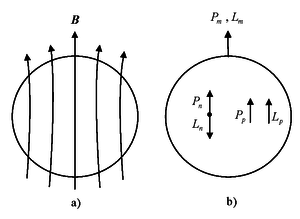
The magnetic moment

Fig.1. The structure of the magnetic field of a magnetar. a) The magnetic lines with induction ~B. ~P_{m}  and  ~L_{m}  are the magnetic moment and the star’s spin. b) The orientation of the magnetic moments and spins of neutrons and protons in the equatorial plane; ~P_{n}  and ~L_{n},   ~P_{p}  and ~L_{p}  are the magnetic moments and spins of neutrons and protons, respectively.

As an effective tool for the study of the proton’s properties we can use the theory of similarity of matter levels. In this theory, one-to-one correspondence is established between the objects of basic levels of matter, and SPФ symmetry predicts similarity in the progress of similar processes. [1] In particular, at the level of stars a strongly magnetized neutron star — magnetar corresponds to the proton. Despite the huge difference in the masses and sizes, there is a great similarity between these objects. If the average matter density of a neutron star is about ~\rho_s = 3.7 \cdot 10^{17} kg/m³, the average density of a proton is about ~\rho_p = 6.1 \cdot 10^{17} kg/m³. The magnetic induction on the surface of a magnetar is more than 1011 T. [2] At a tabular value of the proton magnetic moment of ~P_p = 1.41 \cdot 10^{-26} J/T, the magnetic induction at the proton pole must equal the value of ~B_p = 4.3 \cdot 10^{12} T. It is assumed that the magnetic field of a quarter of neutron stars exceeds the value of 1010 T, and their properties are similar to those of magnetars.

The magnetic field at the center of a neutron star is created mainly by the neutron phase of matter. Here, under conditions of high matter density and strong pressure of about 1033 Pa, the magnetic moments of neutrons are arranged in a parallel way, increasing the general magnetic field. If the neutron spins are opposite to the star spin, then this magnetic field will be close by direction to the star spin. The neutron star mass must be permeated by the magnetic filaments, just as it has been already discovered in ordinary superconductors on the Earth. [3] However, at the assumed threads’ thickness of 10−13 m the magnetic field induction in the filaments is very high — of the order of 1011 T.

To estimate the magnetic moment ~P_m   of the magnetar, according to the theory of dimensions of physical quantities and the theory of similarity, we must multiply the magnetic moment of proton by the corresponding similarity coefficients:

~P_m = P_p (P^{1,5} \Phi^{0,5} S^2) = 1.6 \cdot 10^{30} J/T.

Here ~P= 1.4 \cdot 10^{19},   ~\Phi = 1.62 \cdot 10^{57}   and  ~S = 2.3 \cdot 10^{-1}   are the coefficients of similarity in size, mass and velocities, respectively, [4]  as it follows from the similarity of matter levels.

On the other hand, if the magnetic moments ~P_n   of all nucleons (mainly neutrons) that make up the magnetar, have the same direction, then the magnetic moment equals ~P_{max}= \Phi P_n =1.6 \cdot 10^{31}  J/T, which is an order of magnitude greater than ~P_m . Hence it follows that in the formation of the magnetic moment of the magnetar practically all the particles are involved, of which it consists. But then the proton, similarly to the magnetar, is an object with the maximum possible magnetization of its matter. The experimental dependences of the charge density and the density of the magnetic moment of the proton are close to each other. Then it can be concluded that the contribution to total magnetic moment of the proton is made by individual magnetic moments of the proton matter, just as it happens in magnetars.

From the standpoint of classical electrodynamics, the magnetic moment of the proton is anomalous – it is 2.79 times larger than the nuclear magneton, that is the magnetic moment of a particle with the mass and charge of the proton, which has the quantum spin of the proton equal to ħ/2 (ħ is the Dirac constant).

The maximum magnetic moment of the proton can be expressed in terms of its spin using the formula for a rotating charged ball:

~P_{p max} = \frac {e}{2 M_p}L_{p max} ,

where ~e   is the elementary charge, ~M_p   is the proton mass, and the maximum spin is determined by the formula:

~L_{p max} =I_p \omega_{max}= \frac { I_p V_{ max }}{R_p}= 0.4 M_p R_p V_{ max }.

Here ~ I_p   and  ~ R_p   are the moment of inertia and the proton radius, ~ V_{max }=\omega_{max} R_p   is the maximum velocity at the proton’s equator, ~ \omega_{max}   is the maximum angular velocity of rotation. The formula for the magnetic moment ~P_{p max}    is obtained by integrating over the proton volume and is based on the condition that the electric charge of the proton is uniformly distributed over its volume, and during the proton’s rotation this charge creates the magnetic moment. The quantity ~ V_{max }  can be found from the equality of the centripetal force and the gravitational force at the equator:

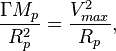
~\frac { \Gamma M_p}{ R^2_p } = \frac { V^2_{max}}{ R_p } ,

where ~\Gamma   is the strong gravitational constant.

For the magnetic moment of the proton we obtain the expression, which gives almost exact tabular value of the magnetic moment:

~P_{p max} =0.2 e \sqrt{\Gamma M_p R_p}.\qquad \qquad (1)

If we take into account that the magnetic moment of the proton is determined by the standard formula:

~P_{p } = 2.79 \frac {e \hbar}{2 M_p} ,

then from comparison with the expression for ~P_{p max}  it follows that the maximum spin of the proton is equal to ~L_{p max}=2.79 \hbar.

As we can see, there is a close relation between the magnetic moment and the rotation of the positive volume charge of the proton with limiting angular velocity. As a result, the magnetic moments of the proton matter particles are oriented by the general magnetic field and support this field, even during the subsequent deceleration of the proton’s rotation. This situation explains the anomalous magnetic moment of the proton in comparison with the nuclear magneton and corresponds to the structure of the magnetic field of the magnetar, shown in Figure 1.

The attempts to calculate the electric charge of the proton only through the rotation of its magnetic moment or through the internal currents show that the proton charge is created mainly by the internal volume electric charge. An additional contribution to the effective value of the proton charge can be made both by the internal currents and the magnetic moment of the proton matter, taking into account its spin rotation. [4]

The magnetic field induction outside the proton is determined by the formula for the magnetic dipole field:

~\mathbf {B} = \frac {\mu_0}{4 \pi} \left ( \frac {3(\mathbf {P_p}\cdot \mathbf {r})\mathbf {r}}{r^5} -\frac {\mathbf {P_p} }{ r^3}\right ),

where ~ \mu_0  is the vacuum permeability, ~ \mathbf { P_p }  is the proton’s magnetic moment vector, ~ \mathbf {r}  is the radius-vector from the center of the proton to the point, at which the magnetic field is determined.

If we assume that the proton is a uniformly charged ball, then rotation of such a ball at the angular velocity ~ \omega   generates inside it the magnetic field induction for a non-rotating observer, which is found by the formula: [4]

~\mathbf {B_i} = \frac {\mu_0}{4 \pi R^5_p} \left ( \mathbf {P_b} (5 R^2_p -6r^2) + 3 (\mathbf {P_b} \cdot \mathbf {r}) \mathbf {r} \right ),

where ~ \mathbf { P_b } = \frac {\mathbf {\omega} e R^2_p }{5}  is the ball’s magnetic moment vector, ~ e  is the ball’s charge.

The radius

There are several methods to estimate the effective radius of the proton. In literature we can find the charge and magnetic radii as well as the radius found from the cross-sections of particles’ interaction. All these radii can differ from the actual proton radius ~ R_p . Thus, in experiments on electrons scattering by protons the root-mean-square charge radius ~ R_q =7.5\cdot 10^{-16} m was found. [5] The cross-section of nucleons’ interaction with each other, established at energies greater than 10 GeV, equals 38 mbn. [6] In the classical limit we can assume that this cross-section is close to the total geometrical cross-section of colliding particles, that is, to the value ~ 2\pi R^2_p . Since mb = 10−31 m², then we obtain ~ R_p \approx 7.8\cdot 10^{-16} m.

Theoretical calculations of the proton radius were performed by Sergey Fedosin using several methods: by examining the standing electromagnetic waves inside the proton; by equating the difference between the binding energies of the proton and neutron to the mass-energy of the electromagnetic field of the proton; [1] and using the limiting angular momentum of the gravitational field of the proton. [7] These methods provide the value of the proton radius (6.7 ± 0,1)∙10−16 m. If we calculate the proton radius from relation (1), we obtain the value 7.7 ∙10−16 m.

The mass and radius of the proton can be estimated by analogy with the way, in which the masses and radii of neutron stars were found, based on the quantum state of their matter and the relation between the gravitational energy and quantum-mechanical energy. [8] Just as in case of neutron stars, the proton mass is determined by the properties of its matter, as well as by the strong gravitational constant, ensuring the nucleon integrity. Hence, it follows that in every gravitational field of any basic level of matter the objects have only one mass-radius ratio, at which the greatest gravitational energy density is achieved. Besides, the values of the mass and radius are fixed by the laws of quantum mechanics, which points to the significant matter degeneracy. For the relation between the radius and mass of the proton we obtain the formula: [9]

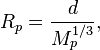
~ R_p = \frac {d}{M^{1/3}_p} ,

where ~ d   is the constant that depends on the properties of the proton matter.

The self-consistent proton model takes into account the non-uniform matter distribution inside the proton (increase in density at the center), the formulas for the binding energy and magnetic moment at maximum rotation. It allows us to determine the central density ~ \rho_c =9.4 \cdot 10^{17} kg/m³ of the proton matter and to estimate the rate of change of the density with the change of the radius. The proton radius equals ~ R_p =8.73\cdot 10^{-16} m and the maximum angular velocity of its rotation reaches 6.17∙1023 Hz. [9] [10] For comparison, the website of Particle data group [11] gives the value of the charge radius of the proton ~ R_p =8.77\cdot 10^{-16} m.

Taking into account the law of redistribution of energy fluxes, for the proton we find the angular velocity of its steady rotation, equal to 2.98∙1023 Hz, at which the equality of the total energy flux of the gravitational field and the kinetic energy flux of the rotating matter is achieved in it. In case if the magnetic moment of the proton and its angular momentum fully coincide in direction, the electromagnetic emission from the proton is zero and it can be in the state of long-term, steady rotation at the constant velocity. [9]

The state of matter

A neutron star contains about 1.62 \cdot 10^{57}  nucleons, and it is assumed that a proton contains the same number of minute quantum particles — praons. This helps us explain why in collision of high-energy gold ions we do not find the gas of quarks and gluons, as is expected in quantum chromodynamics, but jets of almost ideally liquid hadronic matter. [12] At such energies of collisions the hadronic matter cannot be in the form of gas, because it is pulled together by strong gravitation into self-gravitating objects, which over time take a spherical form. [9]

The analysis of the electromagnetic energy and the energy of strong gravitational field in the proton shows that the ratio of the proton mass to its charge is associated with the balance of energies of the field quanta and of the proton matter particles during its formation. The proton charge is close to the limiting value, at which the action of the electromagnetic field begins to destroy the minute particles of the hadronic matter, so that at a greater charge the proton could not exist.

According to the substantial neutron model, the charge and magnetic configurations of the neutron are gradually changing as a result of the weak interaction reactions that occur in its matter. Then a rapid restructuring of the general magnetic field takes place, the negatively charged shell is ejected, turning into an electron. At the same time an antineutrino is emitted, and the rest part of the neutron, positively charged in general, becomes a proton. This process is called \beta^--decay of the neutron, and it shows why the proton charge has a discrete value and is the same practically for all protons – this is a consequence of mass discreteness of neutrons and of the properties of their matter in the strong gravitational field.

The relation between the average pressure ~ p   and the average density ~ \rho   of the proton matter has the form:

~ p = K \rho^{5/3} ,

where ~ K= 8.4 \cdot 10^4   in SI units is the coefficient, which is found through the proton radius, its mass and the strong gravitational constant. [9]

Assuming that the characteristic speed of the matter inside the proton is the speed of light, for the rest energy and the total energy of the proton, in view of the matter energy in the strong gravitational field and the virial theorem, the following relation holds:

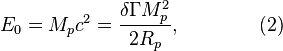
~ E_0 = M_p c^2 = \frac{\delta \Gamma M^2_p}{2 R_p}, \qquad \qquad (2)

where ~ \delta=0.62  is the coefficient that depends on the matter distribution in the proton.

Relation (2) reflects the equivalence of mass and energy as a consequence of the principle of proportionality of the mass and the binding energy of the proton. It also means that in all processes with nucleons the change in their total energy should be taken into account.

Taking into account the expression for the strong gravitational constant, another estimate of the proton radius follows from relation (2):

~ R_p = \frac{\delta \Gamma M_p}{2 c^2} = \frac{\delta e^2}{8 \pi \varepsilon_0 c^2 M_e}= 0.873 fm,

where ~ \varepsilon_0   is the electric constant, ~ M_e   is the electron mass.

The last-mentioned equation can be interpreted as follows. If we put a positron into a neutron and mix the entire matter and charge of the positron over the volume of the neutron, we will obtain a particle close to a proton. Any matter in the proton has the characteristic speed of the order of the speed of light, and the energy equal to the rest energy. On the other hand, the electric energy of the positron during its compression into the nucleon’s volume increases to a maximum and is determined by the proton radius. From expression for the energy (2) it follows that the energy of strong gravitation depends on the proton mass and is equal to the doubled rest energy of all the matter. Similarly, the electric energy depends on the proton charge and is equal to the doubled rest energy of the matter of the positron as an effective charge carrier inside the proton.

Unlike neutrons, protons are practically stable particles, which ensures their maximum prevalence in the nature as part of the hydrogen atom and in atomic nuclei. The stability of the proton in the strong gravitational field is due to the balance of gravitational forces and repulsive forces between the particles of matter inside the proton. On the other hand, the proton matter is stable with respect to the weak interaction reactions, and decays of free protons are not observed. The proton structure is similar to the structure of a magnetar, in which the magnetic moments of neutrons are aligned along the magnetic field of the star, the neutron spins are oriented along the gravitational torsion field of the star, and as a result the stellar energy is minimal.

Composite objects

The proton is the basis of the matter of atoms and it forms a number of compounds with other particles. The coupling between a neutron and a proton by means of strong interaction can lead to formation of a deuteron. The compounds of two protons (diproton) and two neutrons (dineutron) have low binding energy, they are unstable and decay immediately.

In the gravitational model of strong interaction, the strong interaction appears as a result of summation of electromagnetic forces, strong gravitation and forces from the gravitational torsion field. The main components are the gravitational attraction force and the spin-spin repulsion force. When the distances between the particles are smaller than the nucleon radius, the balance of forces and formation of such composite objects, as atomic nuclei, are possible. [4]

Another example is strange particles, many of which are assumed to be the compounds of nucleons and pions. So, Λ-hyperon can consist of fast-rotating near each other and along one axis proton and pion, which are held by strong gravitation and spin torsion fields, [9] and Σ-hyperon is a compound of neutron and pion. The strange Ξ-baryons contain two pions in addition to a proton, and Ω-baryon contains three or four pions, which gives a baryon strangeness, equal to 3. Pions can combine with each other even in the absence of nucleons. An example is K-mesons, consisting of three pions in various combinations.

It is known that at high hadron collision energies, the transverse momenta of arising charged pions with the invariant energy {\displaystyle ~E_{\pi }=M_{\pi }c^{2}=0.1395} GeV have a value from  {\displaystyle ~p_{\pi }={\frac {1}{c}}\cdot 0.3} GeV to  {\displaystyle ~p_{\pi }={\frac {1}{c}}\cdot 0.5} GeV, here c is the speed of light. These pion momenta are considered to be a fundamental quantity for the interaction of hadrons – they depend little on the type and energy of the colliding particles, on the multiplicity of particle production, etc. To explain the origin of such pion momenta, one can use the idea of strong gravitation. If the pion rotates near the surface of the proton in a circular orbit at a speed of {\displaystyle ~V_{o}} , then from the equality

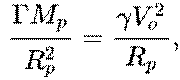
{\displaystyle ~{\frac {\Gamma M_{p}}{R_{p}^{2}}}={\frac {\gamma V_{o}^{2}}{R_{p}}},}

where  {\displaystyle ~\gamma ={\frac {1}{\sqrt {1-{\frac {V_{o}^{2}}{c^{2}}}}}}}  is the Lorentz factor, the quantities  {\displaystyle ~\gamma =3.51} and  {\displaystyle ~V_{o}=0.958c}  are determined. So the pion momentum will be {\displaystyle ~p_{\pi }=\gamma M_{\pi }V_{o}={\frac {1}{c}}\cdot 0.47} GeV.

If the pion moves away from the proton to infinity with a minimum energy, there is the equality for the energy

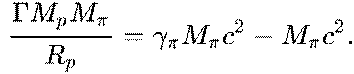
{\displaystyle ~{\frac {\Gamma M_{p}M_{\pi }}{R_{p}}}=\gamma _{\pi }M_{\pi }c^{2}-M_{\pi }c^{2}.}

It gives the Lorentz factor  {\displaystyle ~\gamma _{\pi }=4.2} , the initial pion speed  {\displaystyle ~V_{\pi }=0.971c}  ,

the momentum  {\displaystyle ~p_{\pi }=\gamma _{\pi }M_{\pi }V_{\pi }={\frac {1}{c}}\cdot 0.57} GeV.

 

The nucleon annihilation

In contrast to interactions between protons and neutrons, for annihilation of nucleons as a rule some antinucleons are required. At low energies an antiproton annihilates with a proton with production of 4–5 pions on the average, one of which is neutral and decays into two photons. Additionally, production of K-mesons and less often of certain gamma-ray photons is possible. An antiproton can also annihilate with a neutron.

According to the substantial model, proton-antiproton annihilation is most effective, when they encounter along the line, which is the axis of rotation of both particles. At the same time the spins of these particles must be opposite, and the magnetic moments must have the same direction. Then all the forces, acting from the spins, magnetic moments, charges and masses, are the forces of attraction. During collision, the energy of the opposite rotation of nucleons can fully go into the internal energy of nucleons and heat the matter up to a high temperature. The nucleon matter decays into large parts flying away in all directions, which turn into pions under action of strong gravitation. The rotation energy also can go to electromagnetic quanta. Sometimes in annihilation of nucleons, gamma-ray photons are observed with energies up to 180 MeV, which is about 19 % of the rest energy of nucleon. It is close to the maximum possible rotation energy of one nucleon, reaching almost 20% of the rest energy of nucleon. [4]

Similarly we can consider interaction of antiproton and neutron. The strong gravitational field releases enough energy in order to, under rapid opposite rotation, divide all the matter into parts and scatter it in space. If we calculate the mutual gravitational energy of two nucleons at the moment of their contact, it will be almost equal to the proper gravitational energy of one nucleon. Release of this energy in a collision is not enough to fully scatter the entire nucleon matter, but is enough to divide it into several large fragments with the masses of the order of meson masses.

The reactions of weak interaction

As a rule, protons emerge in the nature in beta-decay of free neutrons in the reaction:

~n^0 \rightarrow p^+ + e^- + \bar{\nu}_e,

in this process electrons ~ e^- and electron antineutrinos ~\bar{\nu}_e  are also emitted. This reaction at the level of transformations in the neutron matter is analyzed in the substantial neutron model.

The reaction of electron capture by proton has the following form:

~ p^+ + e^- \rightarrow n^0 + \nu_e .

When the negatively charged electron matter falls on the surface of the proton, its electric energy of attraction to the proton and the strong gravitational energy are converted into the kinetic energy, which, upon falling, goes into the thermal energy and heats up the matter. Simultaneously, the negative charge of the electron flows into the proton shell and compensates its charge. Since the negative charge cannot penetrate into the central part of a proton due to the high pressure in the matter, the proton core remains positively charged. The electric charge configuration emerges, which is typical for the neutron. Since the proton spin practically does not change, rotation of the negative charge in its shell leads to reversal of the magnetic moment. As a result, a proton is converted into a neutron, with zero total charge and the magnetic moment opposite to the spin.

Transformation of nucleons in interaction with neutrinos takes place with emission of leptons. The following reactions are the examples:

 

  1. ~\bar{\nu}_e + p^+ \rightarrow n^0 + e^+ ,

 

  1. ~ \nu_e + n^0 \rightarrow p^+ + e^-.

 

These reactions take place with very low probability. For example, the cross-section in reaction 1 is equal to 9.4 \cdot 10^{-48}  m² with the energy of antineutrino of 4 MeV, while the strong interaction cross-section during pion-proton scattering has the value of the order of 10^{-29} m² with the energy of colliding particles of about 1200 MeV in the center-of-inertia system. The probability of reactions with neutrinos and the cross-sections of these reactions are directly proportional to the neutrino energies. Obviously, all this is due to the fact that neutrinos consist of beams of minute particles moving at relativistic velocities.

In reaction 1 the electron antineutrino with right-handed helicity transforms the proton into a neutron and a positron. Analysis of this reaction can be conveniently performed at the level of stars, assuming that the stellar electron antineutrino ~\bar{\nu}_{es}   falls on the magnetar, which is the analogue of the proton. This stellar electron antineutrino consists of two parts, including the fluxes of ordinary electron antineutrinos and neutrinos:

~\bar {\nu}_{es} = \left\{ \sum {\bar {\nu}_{e}} +\sum {\nu_{e}}\right\}. \qquad\qquad (3)

The magnetar consists of nucleons oriented by the magnetic field, as is shown in Figure 1. To transform the magnetar into the neutron star, the analogue of neutron, we need to transform the protons of the magnetar’s matter into positrons and neutrons with the help of electron antineutrino. This is possible only when the antineutrino ~\bar{\nu}_{es}   is propagating in the direction from the south to the north magnetic pole of the magnetar. In this case, the right-handed helicity of the fluxes ~ \left\{ \sum {\bar {\nu}_{e}} \right\} and the proper right-handed helicity of antineutrino ~ \bar {\nu}_{e}   in (3) would coincide with the direction of the magnetar’s spin and the spins of protons of the magnetar’s matter. At the same time, the fluxes ~ \left\{ \sum {\nu}_{e} \right\}   of left-helicity neutrinos ~ \nu_{e}   reach the magnetar’s neutrons from the side, in which the spins of neutrons are directed, and produce electrons and protons. Part of the emerging electrons and positrons annihilate, releasing energy and heating up the magnetar’s matter. After accumulating a sufficient number of positrons in the shell, due to their repulsion from the central part of the magnetar, which is positively charged, ejection of the heated matter takes place with formation of a stellar object of positron-type. The magnetar itself is transformed into a neutron star, the neutron’s analogue, since the nucleons in the magnetar’s shell under the action of the fluxes of neutrinos and antineutrinos reverse the direction of their magnetic moment, and the charge gradient appears in the matter due to the electrons produced. This leads to compensation of part of the magnetic field of the magnetar’s core by the magnetic field of the shell, to changing the magnetic field configuration and the sign of the star’s magnetic moment, and to releasing a considerable amount of energy, which contributes to the matter ejection. Ejection of the positively charged matter from the shell of the magnetar means the loss of charge by the magnetar and its transforming into a neutral neutron star. Similarly, an electron antineutrino interacts with the matter of the proton, transforming it into a neutron in reaction 1.

In reaction 2 an electron neutrino with left-handed helicity transforms a neutron into a proton and an electron. Consequently, the stellar neutrino ~\nu_{es}   should also transform a neutron star, the neutron’s analogue, into a magnetar with ejection of part of the shell as an object, which is the analogue of an electron. For this it is necessary to turn the protons and neutrons in the stellar shell into the neutrons and protons in reactions 1 and 2, respectively, with reversal of their magnetic moment. For this to happen, the stellar neutrino ~\nu_{es}  should reach the neutron star from the south pole of its magnetic moment in the direction opposite to the spin of the star. The stellar neutrino has left-handed helicity and consists of the fluxes of electron neutrinos and antineutrinos:

~\nu_{es} = \left[ \sum {\nu_{e}} + \sum {\bar {\nu}_{e}} \right]. \qquad\qquad (4)

Then the left-handed helicity of ~\nu_{es} , as is shown in (4) in square brackets, will correspond to the direction of the star’s spin. In this case, the left neutrinos ~\nu_{e}   will fall onto neutrons, and the right antineutrinos ~\bar {\nu}_{e}   onto the protons of the star from the corresponding south magnetic pole of each nucleon. In reactions 1 and 2 electrons and positrons are produced, which partially annihilate with release of energy. The reversal of the magnetic moments of nucleons in the shell of the star takes place, which leads eventually to transformation of the magnetic field configuration of the neutron star into the configuration of the magnetar, which is shown in Figure 1. In the shell of a neutron star, the neutron’s analogue, there is excess of the negative charge. Rapid changes in the magnetic configuration of the star lead to changes in the magnetic pressure, resulting in ejection of part of the shell’s matter that bears the negative charge. This is equivalent to formation of a new stellar object of electron-type. The star itself becomes a magnetar. From this stellar model we can see, what can happen with the neutron in interaction with the neutrino and how weak interaction reactions occur in the neutron matter. The interactions of nucleons with muons and muon neutrinos are considered in a similar way. As a result, weak interaction in the objects of the same level of matter is reduced to weak interaction reactions at lower levels of matter. Therefore, weak interaction should not be considered a special kind of force, and the use of it for description of gauge W and Z bosons should be considered just as a convenient way of mathematical assessment of phenomena. [4]

The origin

According to the substantial neutron model, the first result of the matter evolution at the level of elementary particles is production of neutrons and nuons from the more massive objects, the analogues of which at the level of stars are the main sequence stars. These objects emerge under the action of strong gravitation as a result of gravitational bunching of scattered matter and produce neutrons, just as neutron stars are formed during collapse of massive stars. Then, in the minute particles of the matter of emerging neutrons weak interaction reactions take place, leading eventually to \beta^--decay of neutrons into protons, electrons and electron antineutrinos. Similarly, weak interaction reactions in the matter of ordinary neutron stars in a cosmologically long period of time of about 2•1015 years should end with \beta^--decay of these stars with formation of magnetars.

Thus the origin of protons is explained without the use of the idea of quarks in quantum chromodynamics and the Big Bang concept, according to which at the time of explosion gluons and quarks should be produced, which then gather in mesons and baryons. In the model of quark quasiparticles, the quarks are considered as quasi-particles, the properties of which are associated with the properties of hadronic matter. The primary particles are considered to be not quarks but nucleons themselves, which in the theory of infinite nesting of matter represent the main objects at the level of elementary particles.

On the other hand, the basic levels of matter are the following: the level of graons – the level of praons – the level of nucleons – the level of stars – the level of supermetagalaxies. [13] Due to the similarity of matter levels, each basic level of matter consists of the objects of the underlying basic level of matter. Hence it follows that protons, neutrons, electrons, and all elementary particles consist of neutral and positively charged praons and negatively charged praelectrons. Fluxes of relativistic praons and graons form the main content of electrogravitational vacuum, generating electromagnetic and gravitational forces between bodies.

 

References

1.       1.0 1.1 Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1.

2.      Heyl J. S. Magnetars. — arXiv: astro-ph 0504077 v1, 4 Apr 2005.

3.      Ruderman Malvin. A Biography of the Magnetic Field of a Neutron Star. — arXiv: astro-ph / 0410607 v2, 2004.

4.       4.0 4.1 4.2 4.3 4.4 4.5 Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9. (2014).

5.      Хофштадтер Р.// Сб.: Физика атомного ядра. — М.: ГИФМЛ, 1962. — С.72‒86.

6.      Барашенков В. С. Сечения взаимодействия элементарных частиц. — М.: Наука, 1966, 531 с.

7.      Fedosin S.G. Sovremennye problemy fiziki: v poiskakh novykh printsipov. Moskva: Editorial URSS, 2002, 192 pages. ISBN 5-8360-0435-8.

8.      Ландау Л. Д. On the theory of stars. — Phys. Z. Sowjetunion, 1932, Vol. 1, P. 285.

9.      9.0 9.1 9.2 9.3 9.4 9.5 Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).

10.  Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451.

11.  J. Beringer et al. (Particle Data Group), Phys. Rev. D86, 010001 (2012). [1]

12.  "'Perfect' Liquid Hot Enough to be Quark Soup". Brookhaven National Laboratory News. 2010. Retrieved 2010-02-26.

13.  Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348‒0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.

See also

External links

 

Source: http://sergf.ru/smpen.htm

On the list of pages