Model of quark quasiparticles

The model of quark quasiparticles is a theoretical model, which is alternative to the ideas of the origin of quarks as a result of the Big bang and to the quark model in Quantum Chromodynamics and the theory of elementary particles. To substantiate the model of quark quasiparticles the theory of Infinite Hierarchical Nesting of Matter, theory of similarity of matter levels, SPФ symmetry, strong gravitation, substantial neutron model and substantial proton model are used. The model of quark quasiparticles shows that quarks are not independent particles but quasiparticles, that is a manifestation of symmetry of the hadrons’ states of matter in the transformation of this matter under the influence of fundamental interactions, as well as in reactions with elementary particles. It follows that the quark model is not final, but rather an intermediate theory of hadrons’ structure.

1 The standard theory
2 The substantial approach

2.1 The phase of hadron matter
2.2 Quarks modeling

3 Hadrons
4 Model justification

4.1 Two-particle reactions
4.2 N and Δ baryons
4.3 Strange particles
4.4 Dipion states
4.5 Baryonium
4.6 Massive vector bosons
4.7 T-quark and the Higgs boson
4.8 Tau lepton

5 Answers to questions
6 Interpretation of the quantum numbers of quarks
7 The symmetry of hadrons as the cause of the idea of quarks
8 See also
9 References
10 External links

The standard theory

Originally the theory of quarks was developed as an artificial theoretical scheme to describe the symmetry of hadrons’ interactions. In chromodynamics the quarks are treated as point objects with not precisely determined mass that make up hadrons – baryons and mesons. There are six types (flavors) of quarks: u, d, s, c, b, t, which are generally denoted by the symbol q. Antiquarks are denoted by tilde or a bar over the quark symbol. It is supposed that baryons consist of three quarks and mesons consist of a quark and an antiquark.

Quarks are considered to have a special charge characteristic – color, as well as quantum numbers that distinguish each quark from other particles. It is assumed that the essence of strong interaction between hadrons is interaction between quarks by exchanging gluons that transfer color. Quark decays result from weak interaction with emission of massive vector W-bosons. Quarks transfer fractional charge and half-integer spin and can be located only inside hadrons (the confinement effect, i.e. color confinement). In this case hadrons do not have color due to color compensation in the quarks that constitute them.

Due to introduction of a number of specific properties and additional characteristics in the structure of particles and the action of new fields the idea of quarks allowed us to put in an ordered system the set of hadrons and to describe the dynamics of their interaction, including particle decays, the estimates of cross-section of their interaction with each other, lifetime, spins and magnetic moments, energy levels and particle masses. Despite these successes the theory has a significant number of important problems, which have not yet been solved.

The principal difficulty of the theory is that in quantum chromodynamics the interaction of elementary particles (quarks, leptons, vector bosons) is considered practically as a point event with particles that do not have the size. Describing such an interaction based on the symmetry of the gauge field theory leads to mathematical divergences, which cannot be fully eliminated, and to deliberate inaccuracies of theoretical predictions.

The substantial approach

Unobservability of quarks in a free state, locality of their interaction, approximation of the quark matter behavior by ideal fluid in collisions with high energy ^[1] lead to the idea that quarks are a special kind of quasiparticles, which are closely related to the hadrons’ matter. Elementary particles have spin (characteristic angular momentum due to self-rotation), electric charge, magnetic moment, and can have a complex inner structure. Both quarks and hadrons are involved in all the four fundamental interactions. It is assumed that during strong interactions quarks are redistributed between hadrons and new quark-antiquark pairs and gluons are produced from vacuum due to its polarization by gluons.

On the other hand, the strong interaction can be explained by the strong gravitation, gravitational torsion field and electromagnetic forces based on the gravitational model of strong interaction. ^[2] The density of the matter inside the nucleon is only a few times greater than the mass density of the neutron star, ^[3] where the matter is in the state of neutron liquid with a small admixture of protons and electrons. Decrease in the neutron star mass below the limit of 0.1 – 0.2 solar masses inevitably leads to transformation of the stellar matter into a less dense phase, similar to the matter of a white dwarf or even an ordinary star, with energy release. ^[4] If we consider the hadrons’ matter in a similar way, then in reactions of particle scattering at sufficiently high energy matter masses can break away from hadrons, with subsequent change in their state and transformation into new elementary particles. In many cases pions are produced (mesons with minimum mass), which from the standpoint of the similarity of matter levels are similar to a neutron star with the mass equal to 0.2 solar masses, which is close to the stability limit of such stars in respect of the state of matter.

Besides, we can also assume that over time the matter of many elementary particles undergoes transformation due to interactions similar to the weak interaction, which leads to decay of these particles. Hence, due to quantization of various properties of elementary particles, complexity of their structure and possibility of different types of interactions, the observed symmetry of hadron properties and their resonant states can be not the consequence of the existence of quarks but the consequence of the intrinsic properties’ symmetry of the hadrons’ matter and of the surrounding fields.

The phase of hadrons’ matter

The α-phase of hadrons’ matter means the same matter as in a magnetized neutron nucleus and the β-phase corresponds to the matter in the neutron shell, which is oppositely magnetized. These phases of matter arise from the substantial neutron model. In this model the magnetic moment of the neutron is composed of the magnetic moments of the nucleus and shell, while the neutron nucleus and α-phase of matter are positively charged, and the neutron shell and β-phase of matter are negatively charged. The total charge of the neutron is zero, and the magnetic moment is determined by the negative magnetic moment of the β-phase of matter, which exceeds in the absolute value the magnetic moment of the α-phase of matter due to the large volume of the shell and the increased magnetic flux in comparison with the nucleus.

Neutron beta-decay occurs as a result of the weak interaction reactions in the neutron matter, the magnetic field structure transformation and the emission of negative electric charge from the shell in the form of electron, with transformation of neutron into proton. In the first approximation we can assume that the magnetic moment P_β of the shell changes its sign and becomes directed the same way as the magnetic moment P_α of the nucleus. Since the sum of magnetic moments of the shell and nucleus should equal the magnetic moment of the proton and their difference should equal the neutron magnetic moment, then we can estimate that P_α = 0.44 μ, P_β = 2.35 μ, where μ is the nuclear magneton. These magnetic moments reflect the fact that the change of sign of the internal volume electric charge density occurs in the middle of the neutron radius. Thus the α-phase and β-phase in the neutron matter are oppositely charged and magnetized.

Quarks modeling

In Fedosin’s model it is assumed that not only nucleons, but all hadrons and hence quarks can be composed of certain combinations of the two above-mentioned matter phases. The composition of quarks is presented in the Table. ^[2]

Quarks’ composition
Quark	The share of α–phase	The share of β–phase
u	1/3	1/3
d	1/3	–2/3
s	–2/3	1/3
c	4/3	–2/3
b	4/3	–5/3
t	4/3	–2/3

According to the table, the ratio of the matter phases for quark u is: u = α/3 + β/3, and similarly for quark b: b = 4α/3 – 5β/3. If we assume that the values α and β correspond to the unit elementary electric charge, then upper quarks u, c, t will have charges +2/3 and lower quarks d, s, b – respectively –1/3 in the units of elementary electric charge.

Hadrons

The composition of α and β for hadrons is obtained by summing α and β composition of the quarks, which are part of these particles. The following Tables show the α and β composition of some hadrons.

Baryons’ composition
Particle	Mass-energy, MeV	Quark composition	α , β composition
p⁺	938.272029	uud	α
n⁰	939.565360	udd	α – β
Λ⁰	1115.683	[ud]s	0
$\Xi^-$	1321.31	dss	– α
$\Xi ^+_{cc}$	3519	dcc	3α – 2β
$\Xi^-_{b}$	5774	dsb	α – 2β

Mesons’ composition
Particle	Mass-energy, MeV	Quark composition	α , β composition
π⁺	139.57018	$u \bar {d}$	β
π⁰	134.9766	$\frac {1}{\sqrt 2}(u \bar {u}-d \bar {d})$	0
K⁺	493.677	$u \bar {s}$	α
K⁰_S	497.648	$\frac {1}{\sqrt 2}(d \bar {s}-s \bar {d})$	2α – 2β
K⁰_L	497.648	$\frac {1}{\sqrt 2}(d \bar {s}+s \bar {d})$	0
D⁰	1864.5	$c \bar {u}$	α – β
$B^0_{s}$	5367.5	$s \bar {b}$	–2α + 2β
$B^+_{c}$	6286	$c \bar {b}$	β
Υ⁰	9460.3	$b \bar {b}$	0

In tables the hadrons of the type $~ \Sigma^0, \pi^0, \eta^0, J/\psi^0$ have zero or indefinite matter phase. It means the absence of uncompensated electric charge in these particles and indicates the matter state that is not the full α- or β-phase. It can be assumed that the matter of these particles is in a mixed state, with α–β or –α + β phases. Typically, such particles have a much shorter lifetime as compared to particles with a different matter composition. An example is the decay $\Lambda \rightarrow p^+ + \pi^- ,$ in which the indefinite matter phase of particle $~\Lambda$ is transformed into α-phase of proton and (– β)-phase of negative pion. Some neutral hadrons clearly consist of both matter phases, with the composition of the form α – β, –α + β, 2α – 2β. In charged hadrons the α- or β-phase of respective sign prevails. The analysis of known magnetic moments of hadrons shows that almost in all positively charged particles the magnetic moment is directed along the spin, while in neutral and negatively charged particles it is directed against the spin. This is due to the fact that prevailing of one matter phase over the other leads to prevailing of the charge and magnetic moment of this phase over the other phase.

Model justification

According to the theory of Infinite Hierarchical Nesting of Matter and SPФ symmetry, the same scenario of new objects formation is repeated at each level of matter: they result from accumulation of matter of lower matter levels under the influence of gravitational and electromagnetic forces, as well as in the decay processes of the matter of higher matter levels, which occur due to different interactions. From this point of view, for production of elementary particles as well as quarks there is no need in the “Big Bang” hypothesis. Thus the well-known problem of the observed absence of antimatter in the Universe is removed, because without the Big Bang there should not be much antimatter. In the model of quark quasiparticles, quarks are the consequence of the symmetry of various phases of hadrons’ matter and of the quantum behavior of particles in their interactions. In particular, in such processes the amount of matter, energy and momentum, characteristic spin, electric charge, magnetic flux and other similar quantities are conserved and redistributed. The results of interactions of elementary particles also depend on the interaction configuration and the corresponding summation (subtraction) of the vector physical quantities of particles. In order to move from the formal quark scheme to real interaction models and to replace quarks as certain particles with quarks as quasiparticles in the form of combinations of hadrons’ matter phases, it is necessary to show that for each reaction with hadrons there is a certain and clear physical mechanism that does not require introduction of a number of new entities (gluons, massive vector bosons, color charges, mixing angles of states, etc.) used to describe the observed symmetry of hadrons.

Two-particle reactions

In some cases particles interact with each other so closely, that they significantly change their state. For example, in the charge-exchange reaction of the negative pion $\pi^- + p^+ \rightarrow \pi^0 + n^0$ , the proton is transformed into the neutron. At the same time the sum of matter phases remains the same before and after the reaction, which is equal to α – β. In connection of pion and proton the total spin does not change, the proton spin is equal to the neutron spin, the spin of pions are approximately equal to zero. It can be assumed that transformation of the proton into the neutron occurs due to annihilation of the positive charge in the proton shell by the negative charge of the pion, followed by magnetization reversal and charge exchange of the proton shell. The electric charge of the pion flows into the proton shell under the influence of the Coulomb force from the positive charge in the center of the proton, which leads to the charge distribution, typical for the neutron (the center is positively charged, the shell is negatively charged). This charge configuration is stable, since the negative charge in the shell repels from itself and therefore does not recombine with the positive charge in the center of the neutron. During interaction with the massive proton the pion loses its primary β-phase of matter, is transformed into a neutral pion with zero-phase of matter and then decays into two gamma-quanta.

Indefinite or zero matter phase can be understood as the state of hadrons’ matter, when it has no full ordering of the magnetic moment and the total charge is equal to zero. The lifetime of a neutral pion is 0.084 fs, converted to the lifetime of a corresponding star by multiplying by the coefficient of similarity in time П = 6.1•10¹⁹, according to the theory of similarity of matter levels, gives 1.4 hours. Among all hadrons, pions have the smallest mass, which is 6.8 times less than the mass of nucleons. The mass of a neutron star, corresponding to a negatively charged pion, is about 0.2 solar masses. If such a star would collide with a magnetar, which is the proton’s analogue at the stellar level, then in not more than 1.4 hours defragmentation would occur with explosive ejection of excess matter and strong emission. This occurs due to both the initial kinetic energy of stars’ motion and release of gravitational and electromagnetic energy during their combination. In this case charge exchange and magnetization reversal of the magnetar shell take place, so that the star as a whole becomes electrically neutral and its magnetic moment changes its sign. The ejected matter and emission can be directed by the magnetic field of the star, creating oppositely directed fluxes (jets), starting at the magnetic poles. This explains the neutral pion’s decay into two gamma-quanta and the short lifetime of this pion.

The energy of the reaction $\pi^- + p^+ \rightarrow \pi^0 + n^0$ can easily be estimated quantitatively for the case, when the proton is at rest and the pion’s kinetic energy is low. When pion and proton are combined, the energy of strong gravitation is released, which can be estimated by the formula:

$E_{\Gamma }= -\frac {k\Gamma M_p M_\pi}{R} ,$

where $~ \Gamma$ is the strong gravitational constant, and $~M_\pi$ are the masses of proton and pion, respectively, $R=0.87 \cdot 10^{-15}$ m is the average distance from the proton’s center to the pion, which is approximately equal to the proton radius. For the absolute value of the energy it equals $\mid E_{\Gamma } \mid = 271$ MeV in energy units. Part of this energy is emitted in the form of two gamma-quanta with the total energy not less than the value 134.963 MeV, which is considered the mass-energy of a neutral pion at rest. Hence it follows that in this case the neutral pion is not an independent particle and it exists as a transitional state of matter on the surface of a massive hadron.

Another reaction of charge exchange is the reaction: $\pi^+ + n^0 \rightarrow \pi^0 + p^+$ . In this case, the positive pion produces magnetic reversal and charge exchange of the neutron shell, turning it into a proton. At the same time the pion becomes neutral, as described above, and decays with emission of gamma-quanta.

In the interaction of the gamma-quantum with the proton, the pion and the neutron can be produced in the reaction: $\gamma + p^+ \rightarrow \pi^+ + n^0$ . The matter composition in the reaction is conserved, since the proton consists of α-phase matter, the pion consists of β-phase matter, the neutron matter composition is α – β, and the gamma-quantum is considered neutral, with zero-phase of matter. The speed of the gamma-quantum equals the speed of light and corresponds to the characteristic speed of the matter inside the proton. Therefore, if we select a wavelength of the gamma-quantum close to the proton size, then the quantum energy would be resonantly absorbed by the proton, and the reaction becomes possible. It follows from the experiment that the reaction cross-section is $\sigma=2 \cdot 10^{-32}$ m², and the required energy $~E_\gamma$ of the gamma-quantum is about 0.3 GeV in the laboratory reference frame. If we assume that $\sigma=\pi R^2_p$ , then for the proton radius we obtain the value of 0.8 fm. The estimated wavelength of the quantum is: $\lambda=\frac {hc}{E_\gamma }=4\cdot 10^{-15}$ m. The simplest resonance condition is placing half of the wavelength on the proton diameter: $~\lambda /2=2 R_p ,$ as for oscillations between two fixed ends. Hence the determined quantity exceeds not more than 1.15 times the current radius of the proton.

One of the problems in the photoproduction of particles is the origin of mass of the newly formed particles. If we use the formalism of the special relativity, then the particle mass or the experimentally determined state of the system of particles is a secondary parameter and is determined with the help of the total energy and total momentum. In such determination, contributions to the mass are made by both the energy and momentum, while the question of retaining the matter amount as a measure of the matter mass is not considered. This follows naturally from the approach, when we consider only the energy and momenta of the initial and final states of the particles, without analyzing the transformation of matter and energy of the particles in the course of their interactions (see the mass–energy equivalence). Taking into account the strong gravitation allows us to add into the energy balance equations the terms associated with the total energy of the particles in the strong gravitational field, and thus to take into account the law of matter conservation of the particles involved in the interactions. ^[5]

N and Δ baryons

The analysis of reactions with elementary particles shows that due to the presence of precise models of particles and their interactions the quark hypothesis becomes unnecessary. This is most clearly manifested in the formation of baryons N and Δ, with the spin ħ/2 and 3ħ/2, respectively (ħ is the Dirac constant). These baryons usually arise from irradiation of nucleons by gamma-quanta, from scattering of electrons and pions in the matter, and are considered nucleon resonances, i.e. the excited states of nucleons with a short lifetime. Composition of nucleons coincides with the α, β-composition of N-baryons, as well as of neutral and singly positively charged Δ-baryons. It is noticed that collision of negative pions with the corresponding energy with nucleons leads mainly to emergence of different resonances of N-type, and collisions of nucleons with positive pions mostly produce resonances of Δ-type.

To form a resonance Δ₁ (1232 MeV), it is necessary that the orbital angular momentum of the pion of magnitude ħ and the spin of the nucleon of magnitude ħ/2 be added together at the moment the pion flies past the nucleon. Although the pion partially spins up the nucleon and transfers its energy of motion to it, the main part of the spin of resonance Δ₁ arises from the orbital angular momentum of the pion, the velocity of which is almost equal to the speed of light. The lifetime of the state Δ₁ is determined by the formula τ = ħ/Γ_k, where Γ_k = 118 MeV is the width of the resonance level. Hence we obtain τ = 5.6•10^–24 s. Based on the given time and orbital angular momentum we determine the minimum distance between the centers of the pion and nucleon (0.86•10^–15 m), which is close to the nucleon radius. ^[2] In order to estimate the angle θ of the pion’s rotation near the nucleon, which occurs in time τ under the influence of strong gravitation and electromagnetic forces, we can write: θ ∙ R_p ≈ c ∙ τ, where θ <111º. In experiments on scattering of pions on nucleons the maxima in differential cross-sections are found at scattering angles of the order 40º .^[6] The binding energy of the resonance is close to zero, due to which it decays quickly into nucleon and pion.

The described pattern is repeated for the resonance N₁ (1440 MeV), with the difference that in this case the orbital angular momentum of the pion and the nucleon spin are directed oppositely and are subtracted from each other, and the lifetime of the state is much less and equals 1.5•10^–24 s. The analysis of other resonances N and Δ indicates that the peculiarities of their emergence in the processes of pions’ scattering on nucleons can be explained by the action of different forces: a) between the magnetic moments of the particles; b) between the spins of the particles; c) the Coulomb force; d) the magnetic Lorentz force; d) the spin-orbit force (the gravitational torsion field from the spins of particles in the strong gravitational field acts on the moving masses of particles). The forces differ in different sets of initial particles with different configurations of interaction. ^[2] If we do not consider a particular interaction model in each case and use the idea of quarks, then the quarks at the resonances in addition to spins must have orbital angular momenta, and the resulting particles should be considered the formal consequence of the symmetry of spatial wave function of the compound system of quarks. In this case, the spin, orbital and spin-orbital interaction of quarks is considered. Apparently, these interactions of quarks reflect the reality in such a way, that they correspond to the forces from magnetic moments and spins of particles, the Coulomb forces, the magnetic and gravitational Lorentz forces, that occur between hadrons in their interaction.

Strange particles

The analysis of the reactions of interactions, decays and models of strange hadrons shows that they can represent a combination of simpler hadrons. ^[5] For example, it is assumed that the hyperon Λ consists of a proton and a pion rapidly rotating around each other along the same axis, held together by strong gravity and spin torsion fields. To calculate the equilibrium condition the equations for the forces and energies are used. Over time, nucleon and pion slowly approximate, collide with each other and Λ-decay takes place. Similarly, it is shown that Σ-hyperon is a compound of neutron and pion. Strange Ξ-baryons are more complex structures, containing a proton and two pions. The composition of Ω-baryons in addition to proton includes three or four pions, giving the baryon strangeness, which is equal to 3.

K-mesons are likely the compounds of three pions and have the following compositions:

$K^{0}_L = \pi^{-} \pi^{0} \pi^{+},$

$K^{0}_S = \pi^{-} \pi^{+} \pi^{0},$

$~ K^{-} = \pi^{-} \pi^{+} \pi^{-},$

$~K^{+} = \pi^{+} \pi^{-} \pi^{+}.$

The difference in the pion configurations of $K^{0}_L$ and $K^{0}_S$ leads to the fact that the lifetime of the first kaons exceeds significantly the lifetime of the second, and to the difference between the results of the reactions of interaction with other particles. This allows us to give up the idea of representation of neutral kaons in the form of quantum superposition of two basic states, accepted in the standard theory in order to explain the differences between the two types of neutral kaons, with introduction of the so-called mixing angles of basic states.

Vector Φ-meson with the energy 1019.455 MeV during the lifetime of the order of 1.5•10^–22 s decays into two kaons. If we assume that the velocity of kaons is of the order of the speed of light, during the lifetime of the Φ-meson the kaons will cover the way not more than the length of kaons, composed of three pions. Then it follows that the short-lived state of Φ-meson emerges in close interaction of two mesons, consisting in total of 6 pions.

There are quite long-lived hadrons, which in addition to a strange quark contain charmed quarks and beautiful quarks. The examples are the baryon $~\Xi_c$ with the energy 2471 MeV and the lifetime of 0.112 ps, and the baryon $~\Xi_b$ with the energy of 5792.9 MeV and the lifetime of 1.42 ps. The analysis of the products of their decay shows that the sums of energies of secondary particles can be insufficient for them to be in equilibrium state and to produce a hadron, as it happens in less massive strange hadrons. It could be concluded that charmed and strange hadrons have additional characteristics – their states can emerge in collisions of less massive components, when additional energy is released due to the energy of strong gravitation and transformation of hadrons’ matter.

Dipion states

Meson resonances emerge in different processes, for example in photoproduction, in collision of electron-positron beams, in scattering of pions on nucleons, in annihilation of nucleons, etc. Some resonances like f and ρ almost always decay into two pions. The lifetime of these resonances does not exceed 1.6•10^–23 seconds. ^[7] During this time two fast-moving matter masses, when they collide, can make not more than one revolution around the common center of mass, and then decay, turning into two relativistic pions (or into other mesons).

Resonance $~f^0_{0}(600)$ has the lower limit of the mass-energy of about 400 MeV and zero spin. It can be considered as the result of almost central collision of two pions, each of which has the kinetic energy of more than 61 MeV at the velocity more than 0.72 с, where с is the speed of light. The lifetime of this resonance is little, so that the pions immediately fly apart with semiflexible scattering.

The spin of ρ-meson (775) is equal to ħ, and it can be understood in the situation, when two colliding pions during 4.5•10^–24 seconds closely interact with each other at the minimum distance 2R, and then scatter in different directions. The total energy per one pion equals half of the mass-energy of ρ-meson, i.e. 388 MeV. Hence, using the relativistic formula, that relates the mass and energy, it is easy to find the momentum of each pion. At least one of the pions is charged, and the second is either neutral or oppositely charged, depending on the availability and the sign of the charge of the ρ-meson. The moving pion creates around itself the field of strong gravitation, which has the gravitational field strength and the gravitational torsion field $~\Omega .$ In case of counter motion of pions, at their velocity of the order of the speed of light, the force from the torsion field is summed up with the force of gravitational attraction, doubling the latter one. ^[3] In the first approximation, we can equate the gravitational acceleration and the centripetal acceleration of particles relative to the center of mass, as they move close to each other:

$\frac {\Gamma M}{2R^2} = \frac {p c}{R},$

where and are the rest mass and momentum of the pion, is the speed of light as the approximate velocity of the pion.

From this equality we obtain R = 2•10^–16 m. On the other hand, for the meson spin we can assume that ħ = 2 p R, from which R = 2.7•10^–16m. Consequently, the radii of pions should be greater than R, so that in collision of pions the ρ-meson (775) will be manifested.

Among the mesons there are particles with large values of spin, for example, $~f_{6}(2510).$ If we assume that the spin of this particle with the size 6 ħ arises from the interaction of two pions, then the half of the smallest distance R between the centers of pions will equal 4.7•10^–16 m. The pion radius will apparently be even more, as it follows from the calculations, ^[5]and from the experimental cross-sections of interactions of pions on each other at high energies.

Dipion state with the lowest possible energy, equal to the sum of the rest energies of two pions, is observed in a number of reactions, such as in kaon decay into three pions or two pions and leptons. ^[8] The coupling between the positive and negative pions has its special name – pionium. Since the standard theory has difficulty in explaining the dipion states, various explanations are suggested, for example, by introducing the anisotropic component into the strong interaction, due to deformation of the Minkowski space metric near the particles. ^[9] If we proceed from the idea of strong gravitation, then compound of two pions is as possible as in the strange particles and atomic nuclei, due to the balance of the gravitational force and spin-spin interaction, arising from the gravitational torsion fields. ^[5]

Baryonium

By definition, baryonium production requires combination of two quark-antiquark pairs. In annihilation of proton and antiproton we can often observe meson with quantum numbers $~J^{PC}=2^{++}$ (J – spin, P – parity, C – the eigenvalue of charge conjugation operator). This meson decays into pions or meson pairs of the type $\rho^0 \bar{\rho^0},$ and often it is considered not from the point of view of quarks, but as weakly bound and decaying state of two baryons. There are other examples of baryon states, ^[7] such as that decays into $K^{*0} \bar{K^{*0}},$ and in which decays into pairs $\Phi^{0} \bar{\Phi^{0}}$ are observed. It is known that some massive mesons can decay not only into mesons, leptons and photons, but also into baryons and antibaryons, where the latter is the state of baryonium.

In some researches, attempts are made, instead of using the quark model, to describe the hadron states at the level of simpler hadron constituents. For example, the hyperon Λ(1405) is considered as a dynamically bound state of nucleon and kaon, ^[10] and the scalar mesons f(980) and a(980) are considered to be molecule of kaon and antikaon. ^[11] Hadron molecules of kaon, antikaon and nucleon are considered in ^[12] by solving the Schrödinger equation for the wave function of the three particles and by using two interaction potentials assumed in the model. In ^[13] it is proved that many resonant states N, Δ, Λ, Σ, Ξ, Ω are dynamically bound states of vector mesons (such as ρ and ω) with baryons, which are part of baryon octet with nucleons and of decuplet with Δ.

Massive vector bosons

In the quark theory, weak interaction, including the decays of quarks, is usually limited to production of intermediate bosons as carriers of interaction. In contrast to massless photons, in electroweak theory W and Z bosons have large mass, which corresponds to the expected small radius of their interaction and the Fermi constant value for weak decays. Boson masses $W^{\pm}$ , according to the experiments, are equal to 80.398 GeV and the mass $~Z^{0}$ equals 91.19 GeV. Intermediate bosons were discovered in collisions of colliding beams of protons and antiprotons in 1983. They were determined from decay, in which W-boson decayed into an electron (positron) and an electron antineutrino (neutrino), and Z-boson decayed into an electron and a positron, while leptons had higher energy and flew in opposite directions. It is believed that at low energies, the weak interaction is performed by virtual W- and Z-bosons allowing to describe the interaction formally, but at sufficiently high energies virtual bosons become real and give symmetrical decays of leptons.

In the model of quark quasiparticles there is another explanation for the fact that at high energies of nucleon and antinucleon collisions such particle states occur, which are explained as W- and Z-bosons. Let us move on from elementary particles to the level of stars and consider collision of two neutron stars, which are the analogues of nucleons. A typical neutron star has the characteristic speed of nucleons $C_{s}=6.8\cdot 10^{{7}}$ m/s. At the same time, the characteristic pressure over the star $P_{s}=8.5\cdot 10^{{32}}$ Pa is related to the average density $\rho _{s}=3.7\cdot 10^{{17}}$ kg/m³ of the star by the formula:

$P_{{s}}=\rho _{s}c^{2}(\gamma _{s}-1),\qquad \qquad (1)$

where is the speed of light, $~\gamma _{s}$ is the Lorentz factor of nucleon motion in matter averaged over the volume of the star.

Relation (1) is written similarly to how static pressure is expressed in the relativistic formula for pressure according to. ^[14]

To produce intermediate bosons it is necessary that the energy of a proton and an antiproton in their collisions were 270 GeV, which is 287 times greater than the rest energy of proton. In collision of two neutron stars, the kinetic energy of which is 287 times greater than the binding energy of the star, the dynamic matter pressure occurs, which is approximately equal to $~P_{{sd}}=287P_{s}.$ As the pressure increases, the average mass density increases as well. In the approximation of uniform nucleon gas, the following relation exists (in SI units) between the pressure and density of the neutron star: ^[5]

$P=5990\rho ^{{5/3}}.\qquad \qquad (2)$

At the center of a stationary neutron star, the Lorentz factor is maximum and equals $~\gamma _{{cs}}=1.04$ , and at the center of a nucleon it reaches the value of 1.9.^{[15] From} relation (2) it follows that the dynamic matter pressure $~P_{{sd}}$ corresponds to the density $~\rho _{{sd}}=287^{{3/5}}\rho _{{s}}$ . We substitute $~P_{{sd}}=287P_{s}$ , $~\rho _{{sd}}=287^{{3/5}}\rho _{{s}}$ and $~\gamma _{{sd}}$ into formula (1) instead of $~P_{{s}}$ , $~\rho _{{s}}$ and $~\gamma _{{s}}$ , and then compare the result with (1) for $~\gamma _{{s}}\approx \gamma _{{cs}}$ . This gives the average Lorentz factor $~\gamma _{{sd}}=1.385$ for nucleons, which is a consequence of the rapid transition of kinetic energy of the collision into internal energy of the stellar matter. When two neutron stars collide, it turns out that in the resulting object, due to the difference between $~\gamma _{{sd}}$ and $~\gamma _{{cs}}$ , the speeds of nucleons significantly exceed the maximum speed of nucleons of a stationary neutron star. This leads to the impossibility of existence of the composite object as a whole, and to the decay of this object.

The outcome of a collision of two neutron stars depends significantly on the interaction energy, the presence of an electric charge in these stars, and orientation of magnetic moments and spins of the stars. A neutron star must be a positively charged magnetar to be an analogue of a proton, and must be negatively charged to be an analogue of an antiproton. A collision of such stars with sufficient energy and momentum results in the emission of a portion of magnetized matter, charged positively or negatively, from the surface of the stars, or the emission of both positively and negatively charged matter. The emissions of this matter are accompanied by strong electromagnetic radiation, as well as the emission of stellar neutrinos and antineutrinos from the entire volume of the stars.

The presented picture at the level of elementary particles describes the birth of W- and Z-bosons in the collision of protons and antiprotons of the corresponding energy. In this case, the energies and momenta of matter and radiation become sufficiently close in magnitude, explaining the symmetrical emergence of pairs of leptons in the form of an electron (positron) and antineutrino (neutrino), an electron and a positron.

T-quark and the Higgs boson

The most massive t-quark was discovered in 1995 in experiments at the Tevatron collider. In collisions of protons and antiprotons with an energy of 980 GeV per nucleon, the t-quark emerged as a state with the energy 173.1 GeV, in its decay to b-quark and W-boson. The energy 980 GeV exceeds 1045 times the rest energy of the proton. If we calculate the dynamic pressure in the matter of a neutron star using a stellar model and estimate the maximum density of the matter using (2), we can find the average Lorentz factor of the particles of this matter from (1): $~\gamma _{{sd}}=1.645.$

The obtained Lorentz factor $~\gamma _{{sd}}$ becomes close to the Lorentz factor at the center of the nucleon, equal to 1.9. This means that when stars collide with such a high energy, the nucleons of the stellar matter themselves begin to collapse. The same thing happens in collisions of protons and antiprotons with an energy of about 980 GeV per nucleon. In this case, the nucleon matter, consisting of praons, begins to collapse. The appearance of events with t-quarks shows the presence of some boundary state of interaction of particles of this matter. ^[5] It is curious that the energy of the t-quark is almost exactly equal to the sum of the energies of the W boson and Z boson.

Since 2010 by the detectors ATLAS and CMS, working at the Large Hadron Collider, recorded events with the possible appearance of the Higgs boson. This is a neutral scalar boson particle which has zero spin and positive parity. In 2012, it was announced that the Higgs boson is found with energies of the order of 125 GeV. ^[16]

Tau lepton

Among all leptons the tau lepton is the most massive, its energy is 1.777 GeV, and the lifetime is 2.9•10^–13 s. It was discovered in collisions of electrons and positrons with energies in the center-of-mass system more than 3.54 GeV, when pairs of τ⁺ and τ^– leptons were produced. Tau leptons decay either into a tau lepton-neutrino plus hadrons of pion and rho mesons type, or into a tau lepton-neutrino plus muon (electron) and the muon (electron) antineutrino. ^[1^7]

In order to explain how in collisions of electrons and positrons, muons and even pions are produced, the maximum dynamic pressure reached in the collision zone is considered. Calculation shows that close to the energy in the center-of-mass system of the order of 3.54 GeV, the dynamic pressure of the electron matter becomes equal to the pressure existing inside muons, so that from the matter of colliding electrons and positrons the muon matter phase is formed. ^[5] Then, under the influence of strong gravitation, the muon phase is combined into sufficiently massive objects such as muons and pions, observed in the processes, where the states appear that are treated as tau leptons. Thus, there is no need to use the idea of quarks required for production of mesons in decays of tau lepton states.

Answers to questions

Within the model of quark quasiparticles the problematic issues of the theory of quarks and quantum chromodynamics are discussed as follows:

1) Why are there exactly three generations of quarks, which coincides with the number of generations of leptons? Apparently, this is a coincidence, since there are no other considerations besides possible, but not proven symmetry between quarks and leptons. On the other hand, electrons, neutrons and protons are genetically related by the processes of their production (see the substantial electron model). Muons have their analogues at the level of stars – the white dwarfs, containing the degenerate matter of electrons and ions. The analogues of nucleons are neutron stars with degeneration of neutron matter. Among leptons there is a tau lepton, which can be represented as a state in which, in collisions of electrons and positrons, muons are produced. It turns out, that leptons are correlated rather with nucleons and special matter states inside leptons, than with quarks as some parts of hadrons. Then the connection between generations of leptons and quarks becomes accidental.

2) Why are elementary fermions divided into two types – leptons and quarks? The standard model is extremely simplified from the point of view of spin distribution of elementary particles – they are attributed only quantum spin, either half-integral or multiple of the Dirac constant ħ, any intermediate spin values are not considered. According to the substantial electron model, the electron spin must be understood as a dynamic spin, associated with the change in the orbital angular momentum of an electron in an atom due to the shift of electron cloud center from the nucleus. From the calculations in ^[5] the quantum spin of muon is derived from the characteristic speed of muon matter and is also close to the value ħ/2. This leads to the fact that due to their spin leptons are fermions.

Quarks are correlated with fermions and with the minimum spin ħ/2 due to the necessity of building the spins, observed in hadrons, with the help of the quark spins. However, unlike leptons as real particles, quarks are quasiparticles due to their properties, including their unobservability outside hadrons. All particles can be divided into three classes – leptons, hadrons and field quanta, while hadrons in the standard theory are considered to consist of quarks. Besides, it is believed that leptons do not participate in strong interaction, which differentiates them from quarks. However, from the point of view of strong gravitation, the matter of both leptons and hadrons participates similarly in strong interaction, the difference of field strengths is only quantitative and depends only on the difference in the mass density, but not on the mass. Therefore, division of the leptons and quarks can be considered as a formal consequence of introduction of the idea of quarks.

3) Is the coincidence of the number of colors and the number of generations accidental? Most likely, this is an accidental coincidence. The number of colors is determined by the maximum number of quarks in baryons, which gives new degree of freedom to quarks and at the same time associates it with the color charge as the source of strong interaction of quarks. Though the number of generations of leptons and quarks is the same, but it occurs for different reasons. If the color depends on the internal symmetry of hadrons, the generations of quarks depend on the level of interaction energy, so that there is no direct relationship between the number of colors and the number of generations.

4) Why cannot quark masses be determined precisely? The quark masses are not determined precisely because quarks are quasiparticles, not real particles. The properties of quasiparticle depend strongly on the conditions, in which they are observed, as well as on the theory used for their introduction and description. For example, the block mass of quark is considered in the static case, based on the composition of quarks and gluons inside hadrons. The current mass reflects conversions of quarks in the dynamic case with change in the number of gluons surrounding quarks, therefore it differs much from the block mass.

5) What is the reason of such a large spread in the masses of quarks? In the standard theory inequality of quark masses leads to breaking interactions’ symmetry and to different masses of hadrons in multiplets. In this case, the cause of quark masses is assumed to be their interaction with the Higgs bosons. In this approach, variability of quark masses is unclear. In the theory of quark quasiparticles, quarks are considered as combinations of the phases of hadrons’ matter, which are present in each hadron in the necessary amount, and the question of quark masses is replaced with the question of the difference between hadron masses. In turn, the difference of hadron masses is explained by the different number of simple hadrons (usually nucleons and pions) involved in the construction of their states and by the difference of their energy inside a massive hadron, including the energy of strong gravitation, the gravitational torsion field and the kinetic energy of motion.

6) What leads to the difference of quarks’ influence on the properties of hadrons, beside quark masses? In the standard theory the quarks are divided into up and down, and each type there has different mass. In addition, quarks have their own internal quantum numbers that distinguish them from each other (e.g., strangeness, charm, beauty, truth). It turns out that the difference in the properties of hadrons is reduced to the mass and properties of their constituent quarks. In this picture, after transition from the hadron level to the level of quarks, the question remains – what is the reason for the difference of quarks?

7) What do quarks consist of? The question of quark matter remains the subject of speculation and discussion so far. It is assumed that collisions of hadrons at very high energies turn their matter into the quark-gluon plasma, in which quarks become quasifree. In the standard model, quarks and gluons belong to the fundamental elementary particles. Besides, two types of vacuum are introduced, which are specific to quarks and gluons, the electromagnetic vacuum, as well as the Higgs field that gives mass to all particles except gluons and photons. These vacuums should contain virtual pairs, such as quark-antiquark, gluon-antigluon, electron-positron, vector W and Z bosons, and the Higgs field should contain the Higgs bosons. Quarks and gluons outside hadrons, as well as W and Z bosons can exist only in transitional state, immediately turning into hadrons or other particles. Quarks inside hadrons wear “coats” of gluons and float among the clouds of virtual particles. It is obvious that in the standard model it is impossible to solve the problem of quarks’ composition. One of the obstacles is the fact that an unlimited number of particles with the spin ħ for gluons and ħ/3 for quarks, including the spins of virtual particles, is admitted in this model. This obvioulsy contradicts the theory of Infinite Hierarchical Nesting of Matter, in which each object is infinitely divisible, and the characteristic spin of the matter particles, that make up the object, is significantly less than the characteristic spin of the object. Meanwhile, in the standard model it is still considered possible that the strong interaction of pions with each other is performed by pions, but the virtual ones. It implies introduction of the idea of self-closure of interactions of a number of known elementary particles, without the need to involve deeper levels of matter, and inevitably leads to inability to explain the essence of phenomena.

8) What are the sizes of quarks? In attempts to find quarks in hadrons and to separate them from each other high-energy particle collisions are used. With increasing of energy, the particles can penetrate each other more and more, breaking into pieces and then flying apart. The analysis of secondary particles shows that quarks, if they exist, behave as point particles. Recent experiments at relativistic ion collider in Brookhaven have shown that nucleon matter can be heated in collisions up to 4•10¹² degrees. In this case, it behaves similarly to a liquid with very low viscosity, ^[18] and not like free gas of quarks and gluons, predicted by chromodynamics. In contrast to gas, in liquid there are forces of attraction, and this attraction property of hadrons’ matter is predicted by strong gravitation. In the substantial neutron model, the hadrons’ matter, like the matter of neutron stars, consists not of three quarks, but of a set of smallest particles (praons), which allows them to behave like a liquid with low viscosity. From experiments it also follows that the bunches of oppositely charged particles move opposite to one another from the collision zone and rotate in opposite directions according to the sign of their charge, as it happens in a magnetic field. ^[19] This can be explained by the fact that the forces, arising from the torsion field of strong gravitation, in case of rapid rotation of particles exceed significantly the electromagnetic forces and can effectively influence the hadrons’ matter. ^[2]

9) If quarks were formed at the beginning of the Big Bang, why is there practically no antimatter from antiquarks? The problem of the asymmetry of matter and antimatter production in the Big Bang does not have any reliable solution yet, as well as the cause of the Big Bang. The fact of the Big Bang itself is reasonably questioned, because its consequences could perfectly be explained by other reasons. ^{[20] [2]} Therefore, there is no answer to the raised question in the standard theory. But if there were no Big Bang, then the predominance of matter over antimatter can be explained by the natural course of evolution of matter in space. And according to the theory of Infinite Hierarchical Nesting of Matter, the evolution of matter at any level is prepared by the evolution of matter at the lower and higher scale levels of matter. As a result, the matter can accumulate under the influence of fundamental forces and can break up in the processes with large release of energy, eventually forming a ladder of space matter levels.

10) During formation of hadrons, the energy of strong interaction of quarks should be emitted due to combination of quarks. In what form is this energy emitted and can we discover it? In order to explain the quarks’ confinement in hadrons in the standard theory the interaction potential is usually introduced, containing two terms. The first term has the Coulomb form and can be made positive to ensure the forces of quarks’ repulsion at very small distances (otherwise quarks would simply merge). This term should be proportional to the color charges and inversely proportional to the distance between the quarks. The second term is also positive and is directly proportional to the distance between the quarks, raised to some degree, and is responsible for the increase of the force between the quarks, when they move away from each other. The first term has an ordinary potential form, and the second term is similar to the energy of spring tension. It is assumed that the role of a spring is performed by gluon strings between the quarks. If the quarks in hadron collisions get much energy they fly apart, and the collision energy is converted into the energy of the gluon strings. Upon exceeding certain distance and energy density limit these strings get torn and the gluon energy is converted into quark-antiquark pairs, from which new hadrons are produced. At the moment of formation of new hadrons the quarks inevitably get closer and gluon bonds occur between them. If we use the analogy with springs, in the new hadron we should expect damped oscillations of quarks with the distance between them changing from minimum to maximum. Then the question is, where does the energy of these oscillations eventually go? We can assume that the gluon strings have the property of viscosity and they take all the excess energy of quarks’ motion. Thus the system of quarks and gluons with their color charges gets closed on itself and becomes responsible for all the forces and phenomena. However, a new question arises about the origin of the color charges themselves, as well as other similar questions that remain unanswered. The theory of Infinite Hierarchical Nesting of Matter considers the similarity of matter levels and the similarity of forces, acting between the objects, regardless of their sizes. This approach does not require to introduce quarks and to explain their extraordinary properties. Instead, only fundamental gravitational and electromagnetic forces are considered and the weak interaction is reduced not to forces but to the matter transformation. During formation of any objects, in fundamental fields the binding energy is released in the form of quanta of these fields. It is assumed that the quanta of the gravitational field (gravitons) are the neutrinos emitted by particles at different levels of matter, while neutrinos themselves are treated as some form of photons. ^[5]

11) Is there any evolutionary mechanism for generation of quarks and hadrons consisting of them, which is associated neither with the Big Bang concept, nor with the emergence from other high-energy elementary particles at their collisions? In the standard theory the elementary particles such as nucleons and electrons are formed in the Big Bang, where first quark-gluon plasma appeared, which decayed into hadrons and leptons. The drawback of this approach is the analogy with the religious idea of the world’s creation, besides it remains unclear what had existed before the Big Bang. According to the theory of Infinite Hierarchical Nesting of Matter, in order to explain the origin of elementary particles there is no need in the Big Bang, since there is a single evolutionary mechanism for the formation of any space objects, regardless of their size. In the Universe the fundamental forces act by the same laws, due to which formation of new objects of disparate matter can take place. It is assumed that more and more massive bodies are formed under the action of graviton fluxes within Le Sage's theory of gravitation. An example is formation of stars from gas clouds. Just like a star of sufficient mass in the supernova explosion can produce a neutron star, so the matter bound by the action of strong gravitation can be eventually transformed into nucleons. Individual objects can also be formed due division of the system made of a set of associated objects.

12) What is the reason of non-observability of free quarks? The exact reason is unknown, but this is one of the proofs of the fact that quarks are not real particles but quasiparticles.

13) What makes massive quarks decay to less massive and stable quarks? What determines the characteristic time of this decay? Since the properties of quarks due to their non-observability are derived from the properties of hadrons, then from decay of almost all hadrons (except proton) the need of quarks’ decay should follow. In the standard theory the quarks are assumed to be real particles, the basic properties of which, including the instability of quarks with respect to decay, remain unclear. If we treat quarks as quasiparticles, then the cause of hadrons’ decays should be looked for not in the quarks, but in the interactions of simple hadrons, like nucleons and pions, which are part of many massive hadron states, with each other and in the transformation of the matter of these simple hadrons, with regard to their electric charges and the strong gravitational field.

14) What is the relationship between the gluon field, ensuring strong interaction between quarks, and the electromagnetic and gravitational fields of quarks? At the level of elementary particles in the standard theory three types of interaction are usually considered – strong, weak and electromagnetic. Due to the small mass of quarks their gravitational interaction is neglected. If for the strong interaction of quarks, including change of their color charge or confinement in a hadron, gluons are required, then charged W-bosons are required for the change of quark flavor in the weak decay. Quarks have charge, decay into other quarks and W-bosons, and participate together with these bosons in the electromagnetic interaction. Gluons themselves have no electric charge and are not directly associated with the electromagnetic field, but nevertheless can produce quark-antiquark pairs, carrying the charge. This is possible due to the assumption existing in the standard theory that energy is a) can be converted into mass; b) can exist only in the form of particle-antiparticle. However, the conversion of energy into mass contradicts to the law of conservation of matter, which is part of the law of conservation and change of carriers. ^[21] On the other hand, in the theory of Infinite Hierarchical Nesting of Matter the strong interaction is associated mainly with the strong gravitation and the gravitational torsion fields, but not with the gluon field. In turn, gravitation, including strong gravitation, as well as weak interaction are explained as a result of electromagnetic radiation at the lower spatial levels of matter. ^[5]

15) How could leptons, that in the standard theory do not participate in the strong interaction, produce at their collisions quarks and hadrons, which are the objects of strong interaction? According to the theory of strong gravitation, it is the basic part of the strong interaction. In addition, contribution into the strong interaction is made by the forces from gravitational torsion fields and the electromagnetic forces, acting between the particles. Just like ordinary gravitation, the strong gravitation is responsible for the integrity of elementary particles and the attraction of their matter, regardless of whether the matter is part of hadrons or leptons (such as electrons and muons). Therefore, strong interaction must exist in leptons, though in electrons it is much weaker than the electromagnetic interaction due to the low mass to charge ratio. However, in interaction between two muons the action of strong gravitetion exceeds the electrical force 23 times, which leads to similarity of interaction between muons and between hadrons. Thus in 2005 the dimuonium state with energy 214.3 MeV, which decays into positive and negative muons, was studied at the research center Fermilab. ^[22] As it was described above for the tau lepton, in collisions of electrons and positrons of sufficient energy, under action of strong gravitation the muon and pion phases of matter arise from the matter of these leptons. The high density of matter of muon and pion phases is achieved due to the energy of collision. At the level of stars, this corresponds to transition of the planetary matter in collisions with relativistic velocities into the state of matter of white dwarfs, and then after merging of white dwarfs into the state of matter of neutron stars.

16) Why do mesons of two quarks and baryons of three quarks prevail, and not hadrons of an arbitrary number of quarks? From the point of view of spin symmetry, all particles have either integer spin (bosons) or half-integer spin, as fermions. Accordingly, in interactions of elementary particles either mesons with integer spin or baryons with half-integer spin are produced. If we assume that quarks have spin ½, then two quarks always have an integer spin, and three quarks have half-integer spin. Taking into account the orbital angular momenta, which are multiple of an integer number in units of Dirac constant, does not change the baryon or meson status of particles. Therefore, in the simplest case it is sufficient to assume that all mesons are composed of two quarks, and baryons – of three quarks. This allows us to cover all possible hadrons, and the particles of an arbitrary number of quarks in the standard theory are simply unnecessary. However, if we assume that division of particles on the basis of an integer or non-integer spin is conventional, and that there are hadron states with intermediate values of spin, then the idea of quarks with half-integer spin also becomes conventional. In this case, the desired spin of certain quarks should decrease, and the possible number of quarks in hadrons should increase. The fact, that the quark approach to explanation of the composition of mesons and baryons is simplified, is proved by the states with inconsistent and contradictory quantum numbers that are periodically found in different mass ranges. One recent example is production of unaccounted muon jets at the Tevatron collider in proton-antiproton collisions at the total energy of 1.96 GeV. ^[23] In collisions with protons not only unaccounted baryon have been found for a long time, but also meson states with such energies as 62 MeV, 80 MeV and 100 MeV, etc. ^[24]

17) What is the meaning of the observed exotic hadrons that do not fit into the standard quark scheme due to the ambiguity of division into quarks? This situation occurs probably due to the incompleteness of the quark theory that considers the particles as real systems of two or three quarks. However, if quarks are only quasiparticles, indirectly reflecting the symmetry of the interaction of particles, many hadron states, instead of revealing certain symmetry, will give quasi-symmetries that do not comply with the idea of quarks.

For example, there are reports about the discovery of hadrons, consisting of four or five quarks; besides, there is assumed the existence of glueballs – the particles, in which the main role is played not by quarks but by gluons G. ^[7] For example, in experiments with negative pions and protons at energies 18 GeV, mesons π₁(1400) and π₁(1600) with quantum numbers J^PC = 1^–+ were obtained. The analysis of experiments shows that π₁(1400) looks like a four-quark state of the type qqqq, and π₁(1600) is a hybrid of quarks and gluons in the form qqG. The discovered charged meson Z^±(4430) counts in favor of multi-quark states, it could have the structure in the form $cu \bar {c} \bar {d} ,$ $cd \bar {c} \bar {s} ,$ or $cu \bar {c} \bar {s} .$ ^[25]

The baryon resonances – the candidates for five-quark states (pentaquarks) include Φ(1860) with the level width less than 18 MeV and possible quark composition $ssdd \bar {u},$ Θ⁺(1540) with the mass 1533.6 MeV and the level width 0.9 MeV, ^[26] as well as Θ⁰_c(3100) with an estimated quark composition $uudd \bar {c}.$

The well-known organization Particle Data Group has been collecting for a long time the data on the properties of elementary particles and their annual updates. It has gathered a significant collection of references to experimental works, according to which a great number of states of particles is discovered that clearly do not fit into the standard quark model. ^[27]

18) What prevents the virtual quarks from the quark sea from being combined, like valence quarks, and from forming new hadrons, thus creating mesons, nucleons and matter? According to the standard model, quark or gluon that have a color charge, in case they have excess energy, can transfer this energy to the quark sea with production of a real quark-antiquark pair. Thus, the process of formation of matter from energy is admitted. The philosophical contradiction consists in the fact that energy is a characteristic or a quality of the matter, which therefore cannot produce matter without involving some other source of matter. If we assume that virtual particles are the source of matter, they should have the properties of real matter in order to produce real particles. In this case, how can this virtual matter be hidden from observation in the experiment? It is obvious that this question has no answer, and we can only guess what is the mechanism of matter conversion from the virtual status into the real one, why the sea of quarks and antiquarks does not disappear in the process of self-annihilation or does not spontaneously generate hadrons. We can avoid contradictions in the theory of Infinite Hierarchical Nesting of Matter, in which instead of the sea of quarks (quark vacuum), gluon vacuum or electromagnetic vacuum, etc., there are many sources of real matter, each of which is a level of matter, nested in one another.

19) What is the mechanism that keeps the quarks and antiquarks of same or different flavors in some mesons from annihilation? Some hadrons consist of a quark and an antiquark of the same flavor, for example: η_c with the energy of 2980.5 MeV and the composition of the charmed c-quark and c-antiquark, and χ_b with the energy of 9859.44 MeV and the composition of the beautiful b-quark and b-antiquark (see quarkonium). Other hadrons are assumed to consist of combinations of pairs of quarks and antiquarks of the same flavor, in the form of quantum superpositions of these pairs. Quarkonium decay to charmonium and bottomium is considered similarly to the decay of positronium, the bound state of electron, and its antiparticle – positron, existing until their annihilation. Due to the absence in the standard theory of clear justification of interaction between the quarks, taking into account the origin and nature of their color charges, the problem of annihilation cannot be solved completely.

20) Is there a relationship between the symmetry of quarks, leading to combining of hadrons in multiplets and supermultiplets, and the Chew-Frautschi families, built on the basis of the dependence between the spins and the square of the hadron mass? The hadron multiplets include the particles of approximately equal mass, with equal spin and intrinsic parity, but with different electrical charges and the internal quantum numbers similar to strangeness. These multiplets reflect the combinatorics of quark at constant spin of hadrons. If we consider the hadrons of the same type with their resonance states, then in the plane “spin – squared mass” we obtain smooth curves. They are approximately parallel for different types of hadrons, even including mesons and baryons. The reason of parallel curves, the so-called Chew-Frautschi plots, in the standard theory is unknown, as well as their relationship with quarks and multiplets. If we analyze the dependences of the hadron spin on the square of their mass using strong gravitation, then we find a formula for the slope of the Chew-Frautschi plots, which turns out coinciding with the experimental values. ^[2] For the resonances it is shown that their spin is not associated with the limiting rotation of hadrons as some spheres, but rather with the orbital angular momentum of the particles, which form the resonance. Simple multiplets can be understood not as a consequence of symmetry of uds-quarks, but as a result of combinations of α-phase and β-phase of hadrons’ matter, that are part of nucleons and pions, with the property of combining of these particles in hadron states that are characteristic of strange particles. ^[5]

21) How does strong interaction between the quarks inside hadrons turns into strong interaction between the quarks of different hadrons, for example in the atomic nucleus? As the model of interaction of quarks inside hadrons gluon strings are often used which connect the quarks and do not allow them to leave the hadron. It is believed that the potential of such an interaction is short-range. This means that if a quark from the outside will acquire sufficient energy and fly out of the hadron, then the energy density of the gluon string at some point will exceed the limit, the string will be broken with formation of a quark-antiquark pair from gluons, after that hadronization of all quarks into new hadrons will take place. The problem with the strong interaction between hadrons results from the fact that quarks and gluons in the unexcited state do not leave hadrons because of the color confinement. How then are gluon connections between quarks of different hadrons established, which are necessary for the strong interaction between hadrons? In this case, the standard theory involves the idea of using not gluons, but whole hadrons (mostly pions) as the field quanta of strong interaction. This idea is not new, since it repeats the quantum theory, in which electromagnetic interactions between the charges are performed by photons. The significant difference however is that the electromagnetic interaction is a priori potential (the work in the field depends only on the initial and final points, but not on the path of charge transfer), and the fact that the same holds for the strong interaction performed by exchange of gluons or hadrons is not proven. In addition, photons have zero mass, and their range is not restricted, while pions have significant mass. Since there are no real pions between the interacting hadrons, it is assumed that the strong interaction is performed by virtual pions as well as by other hadrons with various degrees of their contribution to the interaction. From this, we can see that the strong interaction between hadrons again is reduced to hadrons, so that there is inadmissible from the point of view of philosophy self-closure of theory and the absence of essential explanation of phenomena. The situation changes if we use the theory of strong gravitation, in which the strong interaction between hadrons and in the hadrons’ matter occurs by the same laws.

22) Is it possible in the framework of quantum chromodynamics to derive from the first principles the description of quarks’ interaction, which leads to confinement? It has not been done so far, because the first principles for quarks are secondary – they are derived from the properties of hadrons, but not from the properties of quarks as such, due to unobservability of quarks. Besides, in the model of quark quasiparticles the definition of quarks’ interactions does not have the meaning of primary matter and can be used only for qualitative estimates of interactions, but not for precise predictions.

23) How do the axisymmetric properties of hadrons with respect to the preferred direction arise from the discrete symmetry of the quark structure of hadrons (two quarks inside mesons and three quarks inside baryons)? We will consider a positive pion, consisting of u-quark with the charge (⅔ e) and d-antiquark with the charge (⅓ e), where e is the elementary charge. Block mass-energies of these quarks, based on their content in the nucleon, are approximately the same and equal to 310 MeV. However, their current mass-energies, manifested in interactions with other hadrons, are different and much less – about 3 MeV and 5 MeV, respectively. The mass-energy of a pion is equal to 139.567 MeV, which causes the block values of quark masses no more than 70 MeV. Consequently, it is assumed that gluons should bear the main part of the hadron mass instead of quarks.

On the other hand, the hadron spin is determined by the quark spins. Thus, in a pion the quark spins must be opposite, giving zero spin (on condition there is no orbital motion of quarks). In this regard, there is a question – how can almost point quarks with low mass have a spin equal to ħ/2? This spin is so great that even a much more massive proton, taken in the form of a ball uniformly filled with matter with the radius 0.873 fm according to, ^{[28] in} case of such spin at the equator, would have the velocity of matter rotation that reaches the value of 0.26 of the speed of light. For a quark in this case the equatorial velocity is much greater than the speed of light, which has no explanation. This situation is similar to the situation with electron, the spin of which in the framework of quantum mechanics also has no rational explanation and is only postulated. An alternative solution for the electron spin is found in the substantial electron model, similarly we should expect another solution for the spin of quarks and hadrons. In particular, calculation of the quantum spin of a pion gives a small but non-zero value, without use of the concept of quarks. ^[5]

As for the quarks’ combination in hadrons other questions arise. For example, what supports the direction of quark spins all the time so that their sum gives the hadron spin? Why is it more suitable for the quark spins in the ground state of a pion to have opposite directions? It can be assumed that there must be spin-spin forces between the quarks that ensure spin orientation in one direction or another and keep them in this state. However, in a simple model of gluon exchange between the quarks such forces are not supposed to exist. Due to the absence of spin, the pion should not have a magnetic moment. Since both pion quarks have no the same mass and their charges differ two times, it remains unclear how the spins of these quarks generate equal and opposite magnetic moments. Moreover, these magnetic moments must have significant size, which is indicated by the magnetic moment of the proton that results from three quarks.

Baryons contain not two, but three quarks, and in contrast to abstract theory, in practice, there is a problem of determining their location in space relative to each other. For example, inside a proton quarks must have some combination uud. Should they be located on the same axis and lie in a plane so that their spins would be perpendicular to this plane? Or can quarks be moving freely relative to each other? In the standard model, there no answers to these questions due to incompleteness of the theory, which follows from the symmetry of hadrons, but not from their essential model.

24) In collisions of high-energy particles new quark-antiquark pairs should be formed that are divided and are included in new hadrons in the processes with multiple production of particles. How are color quarks (antiquarks) combined into new particles, so that these particles are always colorless and the number of quarks in them is such, as is required for mesons and baryons (hadronization problem)? Formally, during formation and subsequent division of a quark-antiquark pair, the quark (and the antiquark) can form by means of gluons new quark-antiquark pairs, which then somehow, according to their color charges, gather together to form hadrons. Hadronization of jets, generated by initial quarks, is called fragmentation. During fragmentation the color charge of the initial quark or gluon, when combined with secondary quarks, should become discolored. This is expected in the theory due to the symmetrical properties of hadrons and quarks anticipated in them, but there is no single specific mechanism of the fragmentation phenomenon.

25) Why do hadron states, formed in different ways but having identical decays, differ from each other in their energy? Example: a) The resonance Δ (1232), that appears in the scattering of pions by nucleons and decays into a nucleon and a pion; b) Interaction of a gamma-quantum with the energy of 300 MeV with a stationary proton leads to formation of a neutron and a pion with invariant energy of the state 1200 MeV; c) The scattering of protons by protons produces a number of narrow resonances, such as the 1004 MeV, 1044 MeV, 1094 MeV, 1136 MeV, 1173 MeV, 1210 MeV, 1249 MeV, etc. ^[29] In the standard theory the hadron states are associated with a set of quarks, which have certain quantum states, regardless of the way of their formation. In this case, the observed difference in energies requires further explanation and is simulated by various approximations. If, however, in the energy balance of a hadron state we take into account not only energy, according to the definition of special theory of relativity, but also strong gravitation, then due to different contributions to the energy balance, different ways of hadron production will inevitably cause different energy states, as it is observed. ^[5]

26) How can we understand the fact that in the standard theory some hadrons should consist not only of a particular set of two or three valence quarks (and indefinite number of virtual quarks and gluons), but are considered to be quantum superpositions of valence quarks, which contain different proportions of combinations of quarks and hence, on the average, fractional by time number of quarks? The examples of such hadrons are Λ-hyperon with the energy of 1115.68 MeV and neutral Σ-hyperon with the energy of 1192.6 MeV, consisting of two triplets of quarks of the form uds ± dus in different states, as well as neutral pion with the energy of 134.97 MeV and meson η with the energy of 547.8 MeV, consisting of quark-antiquark pairs (with u-, d-, s-quarks).

This is a consequence of the quantum-wave approach and the use of unitary symmetry for dividing particles into multiplets, where various combinations of the wave functions of quarks and their combinations are admitted. If we use a probabilistic approach, which is generally accepted in quantum mechanics, it turns out that, for example, some neutral pion, taken at random, can be a quark-antiquark pair of u-type and another similar pion can be a quark-antiquark pair of d-type. In this case, these pairs of quarks inside pions should periodically be annihilated, transforming into each other. The situation for the strange meson η is even more complicated, since the existence of three quark-antiquark pairs is admitted in it, which are annihilated and transformed into each other. From a physical point of view, the meaning of superpositions of quark states in some hadrons and their absence in other hadrons is not clear enough. The specific mechanism of hypothetical oscillations of quark pairs in mesons and quark triples in baryons, as well as the proof of the existence of quark superpositions require complete theoretical justification and experimental confirmation.

Interpretation of the quantum numbers of quarks

Elementary particles have a set of quantum numbers, some of them are unique to hadrons and quarks. For example, the baryon number of quarks is equal to ⅓, the baryon number of baryons is equal to 1, and the baryon number of other particles, including mesons, is zero. We can assume that central parts of baryons are responsible for the conservation of baryon number, their nuclei that do not change or get destroyed in any known reaction, except for annihilation of baryons and antibaryons. The mass, charge and other properties of baryon shells change in reactions with baryons, but not the nuclei. In this case, the nuclei of all baryons consist of the matter of α – phase, which is inherent in the nuclei of neutron and proton. In the state of α - phase the matter is maximally ordered by the magnetic fields and gravitational torsion fields, and therefore it is stable, which leads to conservation of the baryon number. Mesons do not have stable baryon nuclei, so that only nucleon nuclei and the total baryon number are conserved in the interaction with nucleons. In the table above of mesons, for kaon K⁺ the matter composition in the form of α – phase is indicated. This follows from the theory of quark quasiparticles and the idea that all quarks can be formally represented as certain combinations of two phases of hadrons’ matter. However, this is not enough to assign a nonzero baryon number to a particle. For example, kaons can be considered as complexes of three pions, each of which and the kaon itself have the baryon number equal to zero.

Isospin quantum number (isotopic spin) I determines the number 2I +1 of the charge states characteristic of hadrons of the same type, which are part of the respective isospin multiplet. Nucleons have I = ½ and two isospin states – the proton and neutron.

The pion isospin is equal to 1 and corresponds to three charge states of pions. The interaction of pions with nucleons can give not more than four charge states, resulting in isospin equal to 3/2 for resonances Δ. By analogy with hadron isospin, reflecting independence of strong interaction from the charge of particles and the value of their electromagnetic interaction, weak isospin is also introduced for quarks, which differentiates three up quarks and three down quarks. This means that transformations or decays in weak interactions of the quarks of one type are only possible to the quarks of the other type (up quarks transform into down and vice versa). Strong and weak isospins were originally introduced for nucleons and quarks that they consist of. Since the quark composition of proton is uud, and the quark composition of neutron is udd, then replacing u-quark by d-quark (or vice versa) would change the nucleon of one type to another nucleon. This shows that weak isospin of quarks is closely associated with strong isospin of hadrons, which is similar to a relationship between the parts and the whole. In the substantial neutron model, neutron beta-decay and its transformation into proton results from the transformation of neutron matter under influence of weak interaction, that is followed by rearrangement of internal fluxes of electric and magnetic fields. Therefore, weak isospin underlines the relative independence of the weak interaction reactions that occur in the hadrons’ matter due to the strong and electromagnetic interactions in this matter.

The quantum numbers of quarks associated with their spin and charge are determined entirely by and result from the quantitative quark composition and the spins of mesons and baryons. As for the quark masses, they are not determined precisely neither in the quark model, nor in the model of quark quasiparticles, which gives the properties of quasiparticles to the quarks. Let us now consider the differences between the quarks, determined by such a property as flavor. There are four types (flavors) of quarks: s, c, b, t, which are associated with the quantum numbers of: strangeness s, charm c, beauty (bottomness) b, truth (topness) t. For u- and d-quarks there are no special quantum numbers, associated with the flavor.

In the model of quark quasiparticles all quarks and hadrons are expressed as combinations of two phases of hadrons’ matter. This allows us to get closer to the possible structure of hadrons’ matter and shows that quarks are the material representation of symmetry inherent in hadrons and their resonant states. In particular, the difference between the properties of hadrons can be due to the fact that they have different amounts of hadrons’ matter in its two states (α-phase and β-phase), which can be differently charged and magnetized with respect to each other and located in different spatial configurations. The latter is important for strange hadrons, in which there is at least one s-quark. As it was shown in the section devoted to strange hadrons, the presence of s-quark in a hadron can be interpreted as an indication that this hadron has quasi-equilibrium, spatially separated state, which can be decomposed into simpler hadrons. The long lifetime of strange particles results from the way of their production, stability of particles is achieved due to the strong gravitation and the forces from the gravitational torsion fields of particles.

The massive charmed and beautiful hadrons differ from ordinary strange hadrons due to more complex composition of constituent particles, as well as increased energy of their interaction. The hadron states with t-quarks arising at high energies exist for a short time, so that t-quark has time to decay to a less massive b-quark before it becomes part of some hadron. In a sense, t-quark is similar to an intermediate virtual particle. In the model of quark quasiparticles, t-quark is interpreted as manifestation of such a state of hadrons’ matter, in which the threshold velocities are achieved, close to the maximum permissible for this matter.

Another quantum characteristic of quarks, the color charge (color), appeared in order to explain the resonance Δ⁺⁺, in which three quarks uuu must be in the same state, contradicting the Pauli exclusion principle for fermions. Hence we conclude that the maximum number of different color charges should be the same as the maximum number of valence quarks in a hadron, that is three quarks (in baryons) and three colors. In contrast to isospin described by the symmetry group SU(2), rotation in the color space forms the group SU(3). Based on the color charge the strong interaction of quarks in hadrons is explained, which results from exchange of colored gluons between quarks, leading to a change in the color charge and to emerging of attraction forces. However, the idea of force interaction between quarks by means of exchange of gluons, which resembles a quantum-mechanical pattern of interaction between the electric charges by means of exchange of photons, contradicts to the law of conservation of momentum, since two bodies, exchanging neutral particles, can only repel.

In addition to the specific quantum numbers of quarks, in quantum chromodynamics there are a lot of hypotheses and auxiliary quantities, which are necessary for validation of the theory and consistency with the experiment. We can mention anticipated violations of the symmetry of quarks’ interaction due to differences in quark masses, leading to a large difference in the masses of hadrons in each multiplet, as well as to the idea of superposition of neutral quark-antiquark pairs to represent the quark structure of some hadrons (these pairs must annihilate periodically due to the strong interaction, transforming into each other). To match the theoretical results with the experiment various mixing angles in wave functions are introduced, a number of constant coefficients in the terms presumably responsible for certain effects.

Based on the symmetry of color, the existence of eight colored gluons is postulated, so that they could change their color charge in exchange with quarks, without changing the quark flavor. The unique properties of gluons are such that carrying their color charge they can interact not only with quarks but also with each other, which is inexplicable, if we assume that gluons are massless wave quanta. In this case, isn’t it easier to refuse from quarks at all, replacing them with gluons? Though in this case, the hadron masses would be entirely reduced to the mass-energy of massless gluons and the matter would become merely a manifestation of the field. Anyway the expected strong interaction of gluons among themselves is nothing but ultimate absolutization of de Broglie’s idea, according to which the wave–particle duality of particles is performed. With this duality the photons, for example, carry energy and momentum and thus they have the properties of corpuscles as matter particles, but they do not carry an electrical charge, they are involved in electromagnetic and gravitational interactions, but not in the strong or weak interaction. The difference of gluons from corpuscles like quarks consists only in the fact that gluons have zero rest mass, and eight types of charges. Few physicists believe in the full wave–particle duality between matter particles and field quanta at the level of microparticles, assuming that it is valid only in part, in respect of the de Broglie waves and the formulas for the energy-momentum of the special theory of relativity. Accordingly, the idea of gluons, which are even closer in their properties to particles, is viewed with suspicion and skepticism.

Quite unusual is the hypothesis of color confinement in quarks and gluons, since it is unclear how the color charge can be both in quarks as matter particles and in massless gluons as the field quanta. The result is the so-called confinement and the absence of free quarks and gluons in nature. On the other hand, from the point of view of experiment, the quarks are point (less than 10^–18 m) structureless formations inside hadrons, although the hadrons themselves have a radius of the order of 10^–15 m. Then what must the space inside a hadron be filled with and should it be considered as almost absolutely empty? It is assumed that quarks must be surrounded by clouds of virtual quark-antiquark pairs, and the same applies to gluons, thus quark and gluon vacuums are introduced. It turns out that hadrons mostly are filled with unobserved, obviously virtual particles. This picture clearly contradicts the Infinite Hierarchical Nesting of Matter and the theory of similarity of matter levels, in which each hadron has corresponding analogues at every level of matter, including the level of stars. In particular, in a neutron star as the analogue of nucleon we don’t need to search for objects like quarks or gluons, because the physical structure of stars is fairly well known.

Besides quarks and gluons, in QCD in order to explain the weak decays of quarks and transformations of their flavors the massive vector W and Z bosons are required. Although they are considered as quanta – the carriers of weak interaction, they have non-zero rest mass, ensuring very short range of weak interaction. Charged vector bosons can change the electric charge of the quark that emits them to one elementary charge, as well as change the spin to the quantity ħ. The quark emitting such a boson changes its flavor and the boson decays into a lepton and a neutrino or into a quark and an antiquark. Acquiring mass by vector bosons is assumed the result of violation of the symmetry, which is theoretically considered electroweak, and all known particles, in principle, should not have mass, similarly to gluon, except for the hypothetical Higgs boson. But in the real world the symmetry is spontaneously broken, and leptons, quarks and vector bosons acquire mass by interacting with the Higgs bosons.

As we can see, in the standard theory the mass is still reduced to energy and the matter particles – to the field quanta, assuming the latter to be primary. This postulate contradicts the philosophical basis of the matter structure and the theory of Infinite Hierarchical Nesting of Matter. Besides, instead of the standard theory, with short-range massive vector bosons, there is another approach to explaining the weak interaction. According to it, the weak interaction essentially is not a force interaction, like gravitational or electromagnetic interaction, but the result of a long-term transformation of the matter of elementary particles. At the level of stars, this corresponds to phase transitions in the stellar matter, similar to the transformation of the ordinary star matter into the matter of white dwarfs and neutron stars, and the inverse transformation of this matter at the masses of stars, exceeding the limits of the matter stability in the gravitational field. These transitions are accompanied by the collapse of stellar objects, ejection of shells and emission of neutrinos, corresponding to the similar processes in weak decays of elementary particles. A major role in these phase transitions in the stellar matter is played by reactions with elementary particles and nuclear reactions with emission of leptons and neutrinos, as well as breaking of the balance of forces of gravity and pressure in the matter. Therefore, the weak interaction of hadrons and leptons can be reduced again to the weak interaction and matter instability, but at a lower level of elementary particles’ matter. ^[2] In this case, the weak interaction is not a field interaction, so to describe it we actually do not need to introduce any special field quanta. But if we introduce formally the field quanta of weak interaction, such as gauge W and Z bosons, then they would have various extraordinary properties, like mass. Moreover, it becomes necessary to postulate the electroweak symmetry breaking, as well as to introduce the Higgs mechanism.

The symmetry of hadrons as the cause of the idea of quarks

Since in some cases there are alternative models to describe the properties of hadrons and there is no need to involve the idea of quarks, we can assume that quarks are not real particles inside hadrons, but some quasiparticles, reproducing the physical laws and the properties of symmetry inherent in hadrons.

In particular, during hadrons production in reactions of interaction between elementary particles we should take into account the following factors:

The law of conservation of matter, which follows from the law of conservation and change of carriers. ^[21]
The law of conservation of mass-energy of interacting particles.
The law of conservation of momentum.
The law of conservation of angular momentum, taking into account the transformation of linear momentum of particles into quantized angular momentum of the resultant state, subject to the impact parameter limited by the particles’ radii.
The law of conservation of electric charge.
Inequivalence of addition and subtraction of the orbital angular momentum, from the point of view of conversion of motion energy and rotation into the internal energy of particles, which leads to differences in resultant states.
Combinations of different states of hadrons’ matter of interacting particles, which depend in turn on the electromagnetic ordering this matter (magnetic moments, charges, currents in the matter, their orientation with respect to the spin).
Possibility of particles’ combining, just as it occurs in the atomic nucleus.

The additional factors making the internal structure of hadrons more complicated can be the following:

superconductive layers and shells, separating different matter phases from each other or existing in them;
electric currents flowing in the shells and creating additional magnetic moments;
interaction between the magnetic moments from different matter phases and from the currents;
transfer of the angular momentum by the magnetic field and the gravitational torsion field;
gyromagnetic and magnetic-induction effects in the interaction of particles;
interaction of electric charges in the matter of hadrons and between them;
limiting and over-limiting rotation, leading to instability with respect to rotation and to division of resonances into smaller hadrons;
the matter instability under the influence of strong gravitation and electromagnetic forces, due to the reactions of strong, electromagnetic and weak interactions in the matter.

A significant part of hadrons, discovered in experiments, are the bound states of low-mass hadrons, such as nucleons and pions. Some of these states can be called dynamically bound, because the interaction time in them is almost equal to the time of flight of the particles near each other. The dynamic states include almost all the resonance states of hadrons. The typical examples are the baryons N and Δ, as a result of the interaction between nucleons and mesons such as pions and kaons, and the mesons f and ρ as two-pion states. Due to the smallness of electromagnetic interaction in comparison to strong interaction, the symmetry with respect to the charge of identical hadrons is manifested in the form of isotopic invariance (isospin).

Another symmetry associated with the independence of weak interaction in the hadrons’ matter from strong interaction (forming hadrons under the influence of strong gravitation) and electromagnetic interaction (giving charges and magnetic moments to hadrons), is reflected in the concept of the weak isospin of quarks. The special properties of hadrons also include quantization of their properties and discreteness of their states. As a rule, quantization and discreteness follow from the way of hadrons production, the behavior of their matter in the fundamental physical fields. A typical example is neutron stars, which are the analogues of nucleons at the stellar level of matter. The method of formation of neutron stars and the equation for the state of their matter are such that the masses of the majority of these stars fall within a narrow range of acceptable values. The same applies to the formation and evolution of nucleons, which are the basis of matter observed in the Universe.

From the stated above it is clear that considering quarks and hadrons as some compositions of hadrons’ matter in α-phase and β-phase helps to understand phenomenologically different characteristics of elementary particles. The formal substitution of six quarks with two new entities, the matter phases, implies the possibility of further simplification of the theory of hadron structure, generally based on the idea of symmetry of particle interactions and involving the methods of quantum mechanics. In hadron interactions, the matter phases are transformed into each other, so that quarks as compositions of phases are not self-sufficient and therefore unobservable as individual particles. This assigns to the quarks the physical meaning of quasiparticles that do not exist outside of elementary particles. In this case, the theory of confinement loses its sense, since in it unobservability of free quarks is explained by the fact that separation of quarks requires large amount of energy. Another consequence is that the methodology of study of elementary particles needs revision. For example, we need not mathematical-descriptive theories of particles’ structure and interaction, but real essential-material models, including the origin and evolution of particles in a single process of the world evolution. Such models can be presented in the framework of the theory of Infinite Hierarchical Nesting of Matter.

References

"RHIC Scientists Serve Up "Perfect" Liquid". Brookhaven National Laboratory News. 2005. Retrieved 2009-05-22.
^2.0 ^2.1 ^2.2 ^2.3 ^2.4 ^2.5 ^2.6 ^2.7 Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9.
^3.0 ^3.1 Fedosin S.G. (1999), written at Perm, pages 544, Fizika i filosofiia podobiia ot preonov do metagalaktik, ISBN 5-8131-0012-1.
Baym G., Pethick Ch., Sutterland P. The ground state of matter at high densities: equation of state and stellar models. The Astrophysical Journal, 1971, Vol. 170, P. 306–315.
^5.00 ^5.01 ^5.02 ^5.03 ^5.04 ^5.05 ^5.06 ^5.07 ^5.08 ^5.09 ^5.10 ^5.11 ^5.12 Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
Круглов С.П. Пион-нуклонные и нуклон-нуклонные взаимодействия. – в трудах 3 международного симпозиума «Исследования пион-нуклонного рассеяния в ЛИЯФ», АН СССР, ЛИЯФ, Гатчина, 1989, с. 49–85.
^7.0 ^7.1 ^7.2 Yao W.-M. et al., Review of Particle Physics. J. Phys. G, 2006, Vol. 33, P. 1.
14th Lomonosov Conference on Elementary Particle Physics Moscow, 19-25 August, 2009. Measurement of ππ scattering lengths from “cusp” effect in the decay 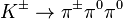$K^{\pm} \rightarrow \pi^{\pm} \pi^0 \pi^0$ and Ke4 decays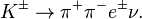 $K^{\pm} \rightarrow \pi^{+} \pi^- e^{\pm} \nu .$
Cardone, M. Gaspero, R. Mignani. Non-standard peak values of the Bose-Einstein correlations and their possible interpretation by a metric description of strong interactions. Eur. Phys. J. C 4, 705-709 (1998). DOI 10.1007/s100529800799.
R. H. Dalitz and S. F. Tuan, Phys. Rev. Lett. 2, 425 (1959); Annals Phys. 10, 307 (1960).
J.D. Weinstein and N. Isgur, Phys. Rev. Lett. 48, 659 (1982); Phys. Rev. D 41, 2236 (1990).
Daisuke Jido, Yoshiko Kanada-En'yo. A new N* resonance as a hadronic molecular state. 25 Jun 2009.
Oset, E. at al. Dynamically generated resonances. 20 Jun 2009.
Fedosin S.G. The potentials of the acceleration field and pressure field in rotating relativistic uniform system. Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://doi.org/10.1007/s00161-020-00960-7].
Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). https://doi.org/10.18052/www.scipress.com/ILCPA.78.39.
Latest Results from ATLAS Higgs Search. ATLAS News. CERN. 4 July 2012.
C. Amsler et al. (2008). "Review of Particle Physics". Physics Letters, B 667: 1. doi:10.1016/j.physletb. 2008.07.018.
"'Perfect' Liquid Hot Enough to be Quark Soup". Brookhaven National Laboratory News. 2010. Retrieved 2010-02-26.
"'Bubbles' of Broken Symmetry in Quark Soup at RHIC". Brookhaven National Laboratory News. 2010. Retrieved 2010-02-26.
Федосин С.Г. Проблемы фундаментальной физики и возможные пути их решения // Сознание и физическая реальность, Т. 9, №. 2, 2004, С. 34 – 42.
^19.0 ^19.1 Fedosin S.G. Osnovy sinkretiki: filosofiia nositeleĭ. – Moskva: Editorial URSS, 2003, 464 pages. ISBN 5-354-00375-X. in Russian.
H. Park et al. HyperCP Collaboration, Phys. Rev. Lett. 94, 021801 (2005).
CDF Collaboration. "Study of multi-muon events produced in p-pbar collisions at sqrt(s)=1.96 TeV".
B. Tatischeff, E. Tomasi-Gustafsson. Search for Low Mass Exotic mesonic structures. Part I: experimental results. 9 Oct 2007.
Choi S.-K., Olsen S.L. et al. Observation of a resonance-like structure in the π^±Ψ΄ mass distribution in exclusive B→K π^±Ψ΄ decays. – arXiv: hep-ex / 0708.1790 v2, 23 Oct 2007.
McKinnon B., Hicks K. et al. Search for the Θ⁺ pentaquark in the reaction (γ d) to (p K^– K⁺ n). – arXiv: hep-ex / 0603028 v2, 4 May 2006.
Particle listings. Particle Data Group. Частицы – не кварковые кандидаты. [2]
Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012). https://doi.org/10.5281/zenodo.889451.
B. Tatischeff, E. Tomasi-Gustafsson. Exotic low mass narrow baryons extracted from charge exchange reactions. 12 Feb 2010.

External links

Model of quark quasiparticles in Russian

Source: http://sergf.ru/mkken.htm

On the list of pages

На русском языке