Preprints
2017, 2017040150. http://dx.doi.org/10.20944/preprints201704.0150.v1
УДК 53.02+530.131:531.62+531.26+531.61+531.422++
537.8+537.213
Энергия, импульс, масса и скорость движущегося тела
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
e-mail intelli@list.ru
В приближении слабого поля в ковариантной теории гравитации формулируется
проблема 4/3 для внешнего и внутреннего гравитационного поля тела в виде
однородного шара. Описывается
зависимость энергии и массы движущегося вещества от энергии поля, сопровождающего
вещество, а также зависимость от характерного размера объёма, занимаемого
веществом. В явном виде вычислены добавки в энергию и импульс тела,
определяемые энергией и импульсом гравитационного и электромагнитного полей,
связанных с данным телом. Обосновывается вывод о том, что энергия и масса тела
могут быть описаны через энергии обычной и сильной гравитации, и через энергии
электромагнитных полей частиц, из которых составлено тело.
Ключевые слова: энергия; импульс; теория относительности; гравитация; потенциалы поля.
Energy, Momentum, Mass and Velocity
of a Moving Body
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
In the weak-field approximation of
covariant theory of gravitation the problem of 4/3 is formulated for internal
and external gravitational fields of a body in the form of a ball. The
dependence of the energy and the mass of the moving substance on the energy of
field accompanying the substance, as well as the dependence on the
characteristic size of the volume occupied by the substance are described.
Additives in the energy and the momentum of the body, defined by energy and
momentum of the gravitational and electromagnetic fields associated with the
body are explicitly calculated. The conclusion is made that the energy and the
mass of the body can be described by the energy of ordinary and strong
gravitation, and through the energies of electromagnetic fields of particles
that compose the body.
Keywords: energy; momentum; theory of
relativity; gravitation; field potentials.
Введение
В релятивистской механике существуют стандартные формулы,
описывающие зависимость полной энергии и импульса частицы с некоторой массой 
от скорости 
её движения:
,
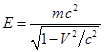. (1)
Зная энергию 
и импульс 
, из (1) вычисляют массу и скорость частицы:
,
. (2)
В (1) и (2) входит скорость света 
. Для неподвижной частицы скорость и импульс равны нулю, а
полная энергия частицы равна энергии покоя:
.
(3)
Соотношение (3) отражает принцип пропорциональности массы и
энергии. В физике элементарных частиц измеряемыми параметрами являются обычно
энергия и импульс, а масса и скорость находятся из (2) и оказываются вторичными
параметрами.
Предположим теперь, что измеряемыми параметрами являются
энергия и скорость частицы. В таком случае из (1) можно вычислить массу и
импульс:
, 
. (4)
Возможен также случай, когда измеряемыми параметрами являются
импульс и скорость частицы, а вычисляемыми величинами становятся масса и
энергия:
,
. (5)
Если скорость частицы задана, то
массу можно найти либо через энергию согласно (4), либо через импульс согласно
(5), в обоих случаях масса должна быть одинакова.
Имеются ещё две возможности сочетания параметров, когда
известны энергия и масса, либо импульс и масса. Это позволяет вычислять модуль
импульса и скорость, либо энергию и скорость соответственно:
,
,
,
.
Из вышеуказанных формул не видно, содержат ли они в себе
энергию и импульс полей, которые присущи частицам и пробным телам. В частности,
пробные тела всегда обладают собственным гравитационным полем и могут ещё нести
электрический заряд и соответствующее электромагнитное поле. В общей теории
относительности (ОТО) считается, что релятивистские энергия и масса тела
уменьшаются за счёт вклада гравитационной энергии. Хотя в ОТО нет однозначного
определения гравитационной энергии и её вклада в общую энергию [1], в
приближении слабого поля предполагается следующее [2]:
,
. (6)
где 
– релятивистская энергия в
гравитационном поле, – энергия в отсутствие
поля, 
– потенциальная
гравитационная энергия тела.
Поскольку энергия отрицательна, то
согласно ОТО масса тела 
должна уменьшаться по
мере усиления поля.
Основной целью данной
статьи является включение в явном виде в релятивистские формулы для энергии и
импульса добавок, возникающих от энергии и импульса полей, связанных с пробными
телами. Все последующие расчёты будут производиться в рамках ковариантной
теории гравитации (КТГ) [3]. Мы будем применять приближение слабого поля, когда
КТГ переходит в лоренц-инвариантную теорию гравитации (ЛИТГ), и становится
возможным сравнить наши результаты с формулами ОТО (6).
Внешнее
гравитационное поле. Проблема 4/3
Предположим, что соотношения (1) – (5) записаны для малой
частицы и через массу учитывают энергию её собственного гравитационного поля.
Если частиц в объёме тела много, то их энергия взаимодействия приводит к
заметному вкладу энергии поля в полную энергию тела. В слабом поле можно
считать, что либо метрика пространства-времени мало отличается от метрики
пространства-времени Минковского, либо гравитационные эффекты замедления
времени и сокращения размеров значительно меньше, чем аналогичные эффекты
вследствие движения тела. В таком приближении ОТО переходит в гравитомагнетизм, а КТГ – в ЛИТГ.
Гравитационные потенциалы от элемента вещества точечных
размеров, находящегося при 
в точке пространства 
и двигающегося вдоль
оси 
с постоянной скоростью
, согласно [4] имеют вид:
, 
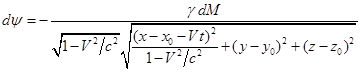, (7)
здесь 
– скалярный потенциал,
– гравитационная
постоянная,
– масса элемента
вещества,
– скорость
распространения гравитации, которую далее для упрощения расчётов будем считать
равной скорости света ,
– координаты точки, в
которой определяется потенциал в момент времени 
,
– векторный потенциал.
Согласно (7), гравитационный потенциал в момент времени от точечной массы 
при её движении вдоль
оси зависит от начального
положения этой массы при . После интегрирования (7) по всем точечным массам внутри
шара на основе принципа суперпозиции получаются стандартные формулы для потенциалов гравитационного поля вокруг движущегося
шара с учётом запаздывания гравитационного
взаимодействия:
, 
,
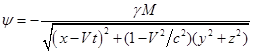(8)
где 
– общий скалярный
потенциал движущегося шара,
– масса шара,
– координаты точки, в
которой определяется потенциал в момент времени (с условием, что при центр шара находился в
начале координат системы отсчёта),
– векторный потенциал.
В (8) предполагается, что шар двигается вдоль оси с постоянной скоростью , так что 
, 
, 
. С помощью потенциалов поля можно
вычислить напряжённости поля вокруг шара по формулам [5]:
,
, (9)
где 
есть гравитационное
ускорение,
– гравитационное
кручение в ЛИТГ (гравитомагнитное поле в гравитомагнетизме).
С учётом (8) и (9) находим:
, 
,
, 
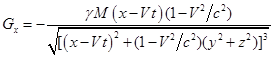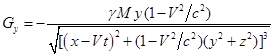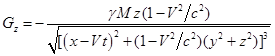, (10)
, 
.
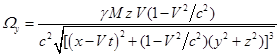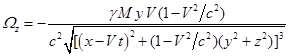Плотность энергии гравитационного поля определяется формулой
[5]:
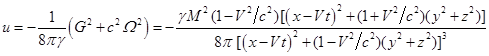. (11)
Полная энергия поля за пределами шара при постоянной скорости
движения не должна зависеть от момента времени. Положим в (11) 
и проинтегрируем
плотность энергии поля по всему внешнему объёму пространства. Для этого введём
новые координаты:
, 
, 
. (12)
Элемент объёма определяется
формулой 
, где:
.
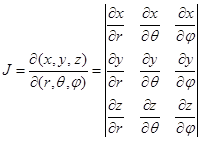Отсюда следует, что 
. Интеграл по пространству от плотности энергии (11) будет
равен:
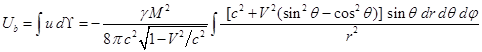. (13)
Учтём, что за счёт лоренцевского
сокращения при движении вдоль оси 
шар должен
представляться эллипсоидом, уравнение поверхности которого при следующее:
.
(14)
После подстановки (12) в (14) становится видно, что радиус 
при интегрировании в
(13) должен меняться от 
до 
, а углы 
и 
меняются так же, как и
в сферических координатах (от 0 до 
для угла 
, и от 0 до 
для угла ). Для энергии гравитационного поля за пределами движущегося
шара находим:
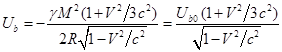, (15)
где 
есть энергия поля
вокруг неподвижного шара.
Предположим, что формула (4) для связи массы и энергии
частицы справедлива также и для гравитационного поля. Тогда можно ввести
эффективную массу поля, связанную с энергией:
. (16)
Рассмотрим теперь вопрос о плотности импульса гравитационного
поля:
,
(17)
где 
есть вектор плотности
потока энергии поля [5].
Подставляя в (17) компоненты напряжённостей поля (10),
находим:
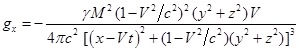, (18)
,
.
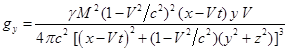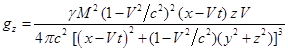Можно видеть, что компоненты плотности импульса гравитационного
поля (18) выглядят приблизительно так же, как если бы на шар со стороны оси 
набегала жидкость, перенося
аналогичную плотность импульса – при встрече с шаром жидкость растекается в
стороны, чтобы слиться вновь на противоположной стороне шара. Интегрируя
компоненты плотности импульса гравитационного поля (18) по объёму за пределами
движущегося шара при 
аналогично (13),
получаем:
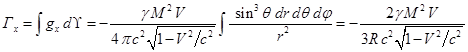. (19)
,
.
В (19) суммарный импульс поля имеет лишь компоненту вдоль оси
. По аналогии с (5) коэффициент перед скоростью 
в (19) можно
интерпретировать как эффективную массу внешнего, передвигающегося вместе с
шаром гравитационного поля:
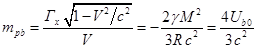, (20)
где 
есть энергия внешнего
статического поля в системе покоя шара.
Сравнение (20) с (16) даёт:
.
(21)
Несовпадение масс 
и 
в (21) составляет суть
так называемой проблемы 4/3, согласно которой масса поля , вычисляемая через импульс поля, при малых скоростях
приблизительно в 4/3 больше, чем масса поля , находимая через энергию поля. Характерной чертой
фундаментальных полей, к которым относятся гравитационное и электромагнитное
поля, является подобие их уравнений для потенциалов и напряжённостей поля.
Проблема 4/3 известна довольно давно в отношении массы электромагнитного поля
движущегося заряда. О ней писали в конце 19 века Д.Д. Томсон, Д.Ф. Фицджеральд,
О. Хевисайд [6], Сирл (George Frederick Charles Searle) и многие
другие. Мы также рассматривали эту проблему ранее, в отношении гравитационного
поля движущегося шара [7]. Сейчас же мы представляем точное решение задачи, не
ограничиваясь приближением малых скоростей.
Гравитационное
поле внутри движущегося шара
Согласно [4] для шара с плотностью вещества 
(измеренной в
сопутствующей системе отсчёта), движущегося вдоль оси , потенциалы внутри шара (обозначенные индексом i ) зависят от времени и имеют следующий вид:
, 
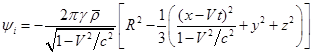. (22)
С учётом (9) вычисляем внутренние напряжённости поля:
, 
, 
,
, 
, 
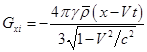. (23)
Аналогично (11) для плотности энергии поля находим:
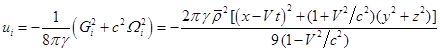. (24)
Из (24) вытекает, что минимальная плотность энергии внутри
движущегося шара достигается на его поверхности, а в самом центре при 
она равна нулю.
Интеграл от (24) по объёму шара при в координатах (12) с
элементом объёма 
даёт:
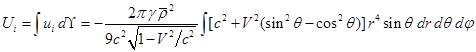. (25)
Движущийся шар выглядит как эллипсоид с уравнением (14), и в
координатах (12) радиус при интегрировании в (25) изменяется от 0 до. С учётом этого для энергии гравитационного поля внутри
движущегося шара имеем:
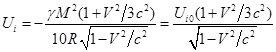, (26)
где 
есть энергия поля
внутри неподвижного шара радиуса 
.
Эффективная масса поля, связанная с энергией, получается
аналогично (4):
. (27)
Подставляя в (17) компоненты напряжённостей поля (23),
находим компоненты вектора плотности импульса гравитационного поля:
, 
, 
.
(28)
Вектор, соединяющий начало координат и центр шара, зависит от
времени и имеет компоненты 
. Отсюда в точке, совпадающей с центром шара, компоненты
вектора плотности импульса гравитационного поля всегда равны нулю. При 
центр шара проходит
через начало координат, и в этот момент из (28) следует, что максимальная плотность
импульса поля 
достигается на поверхности шара, на окружности радиуса 
в плоскости 
, перпендикулярной линии 
движения шара. Это же следует и из (18).
Интегрируем компоненты плотности импульса гравитационного
поля (28) по объёму внутри движущегося шара при в координатах (12)
аналогично (19):
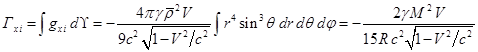. (29)
, 
.
Как и в (19), суммарный импульс поля (29) имеет лишь
компоненту вдоль оси 
. По аналогии с (5) коэффициент перед скоростью 
в (29) интерпретируем
как эффективную массу внутреннего, передвигающегося вместе с шаром
гравитационного поля:
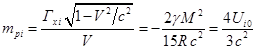, (30)
где 
есть энергия поля
внутри неподвижного шара.
Сравнение (27) и (30) даёт:
.
(31)
Связь (31) между массами поля внутри шара такая же, как и в
(21) для масс внешнего поля, то есть внутри шара тоже имеется проблема 4/3.
Учёт вклада
гравитационного поля в энергию и импульс движущегося тела
Попробуем включить найденные выше соотношения для энергии и
импульса гравитационного поля движущегося пробного тела в виде шара в формулы
(1). Будем считать, что в покое вместо (3) выполняется соотношение:
,
(32)
где 
– полная статическая энергия гравитационного поля снаружи и внутри шара при однородной
плотности его вещества,
– энергия покоя вещества, находимая
таким образом, что она не зависит от энергии гравитационного поля. Для
определения энергии вещество тела следует
разделить на части и разнести их на бесконечность.
Выбор знака минус перед 
в (32) будет обоснован
в последнем разделе. Будем далее анализировать хорошо известный мысленный
эксперимент. Предположим, что вещество шара состоит из материи и антиматерии,
которые в некоторый момент времени начинают аннигилировать и излучать фотоны.
Пусть фотоны летят в противоположные стороны вдоль оси в количестве 
штук в каждую сторону,
так что в конце концов вся масса шара превращается в электромагнитное
излучение. В процессе излучения вследствие равенства импульсов всех фотонов и
симметрии излучения вдоль оси шар остаётся
неподвижным. Чтобы процесс не зависел от изменения радиуса шара, полагаем
радиус шара постоянным независимо от изменения массы. Энергия шара 
из (32) должна
превратиться в энергию фотонов:
,
(33)
где 
– постоянная Планка,
– частота излучения.
Рассмотрим эту же ситуацию в системе отсчёта 
, в которой шар двигается с постоянной скоростью 
вдоль оси и находится при в начале координат.
Считаем, что скорость шара не меняется, несмотря на излучение фотонов. В
системе отсчёта частота фотонов будет
зависеть от того, летят ли они вдоль оси или в противоположную
сторону. Учитывая релятивистский эффект Доплера и (32), для энергии фотонов
вместо (33) будет:
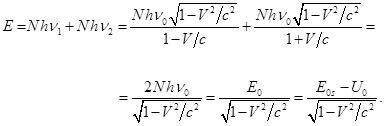(34)
С другой стороны, полная энергия гравитационного поля
снаружи и внутри шара с учётом (15) и (26) равна:
.
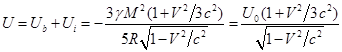(35)
Для энергии вещества и поля движущегося шара имеем:
.
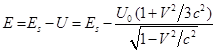(36)
Из (34) и (36) следует:
.
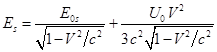(37)
Так как энергия статического поля отрицательна: 
, то в (37) в энергии 
вещества движущегося шара
появляется отрицательная добавка от энергии поля, при этом энергия 
от 
не зависит.
Рассмотрим теперь закон сохранения импульса. До излучения
фотонов импульс движущегося шара состоит из импульса вещества шара и импульса
гравитационного поля, причём с учётом (19) для импульса поля за пределами шара,
и (29) для импульса поля внутри шара, суммарный импульс поля равен:
.
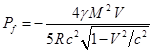Тогда для импульса движущегося шара можно записать:
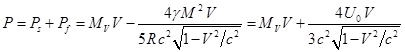, (38)
где 
есть масса вещества
шара как некоторая функция от скорости движения .
После излучения фотонов весь импульс шара и его
гравитационного поля переходит в импульс фотонов:
, (39)
где 
есть энергия (32)
покоящегося шара, равная разности энергии покоя вещества и энергии
гравитационного поля ; кроме этого 
есть энергия фотонов
согласно (33). Из сравнения (38) и (39) следует:
.
(40)
Предположим, что для массы движущегося вещества шара
справедлива формула:
, где 
– наблюдаемая масса
покоящегося тела, 
– некоторая функция.
Здесь мы считаем, что наблюдаемая масса тела, и та масса,
через которую определяется энергия и импульс 
гравитационного поля,
является одной и той массой. Тогда
вместо (40) будет:
.
(41)
Но энергия покоящегося вещества не должна зависеть от
скорости движения, а также в силу (32) от энергии поля неподвижного шара . Поэтому в (41) должно быть 
, откуда с учётом (40) вытекает следующее:
, 
, (42)
где масса 
задаёт энергию покоя
вещества в (32).
Подставим из (42) в (37):
.
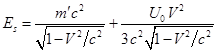(43)
Из (43) следует, что в покое при 
энергия вещества не
включает энергию поля, но при движении в энергии вещества 
появляется добавка,
связанная с энергий поля . Энергия поля делает также вклад в
массу движущегося вещества 
в (42). Полная энергия
движущегося вещества и поля (36) с учётом (43) будет равна:
,
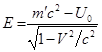(44)
где в случае однородной плотности вещества шара 
.
Из (44) вытекает, что энергия тела увеличивается за счёт
вклада отрицательной гравитационной энергии .
Подставим теперь из (42) в (38), либо из (42) в (39). Это
даёт следующее:
.
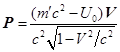(45)
Из сравнения (44) и (45) с (1) видно, что при учёте
гравитационного поля роль суммарной массы вещества и поля играет величина 
. Мы считаем, что 
, то есть суммарная масса вещества и поля есть не что иное,
как наблюдаемая масса 
, которая также определяет гравитационное поле и инертные
свойства тела.
Если нам известна энергия 
в (44) и импульс 
в (45), то из этих
соотношений можно выразить массу вещества и скорость движения
тела 
. В случае однородного шара радиуса 
при вычислении массы
движущегося вещества шара можно записать:
, 
.
(46)
Согласно (46), масса вещества тела определяется не только энергией и
импульсом, но зависит также от среднего размера тела за счёт вклада массы
гравитационного поля в постоянную по величине массу 
.
Заметим ещё, что проблема 4/3 для гравитационного поля (неравенство массы
поля, находимой из энергии, и массы поля, вычисляемой через импульс поля)
оказалась скомпенсированной зависимостью энергии 
в (37) и массы 
в (42) движущегося
вещества от энергии поля . В результате в формулах (44) и (45) энергия поля входит симметрично как
в полную энергию, так и в полный импульс тела.
Анализ
компонент массы и энергии тела
До сих пор мы не уточняли, из каких компонент состоит масса вещества тела, вносят
ли в неё вклад другие энергии, кроме гравитационного поля? Например, что произойдёт,
если тело нагреть? С точки зрения кинетической теории, рост температуры
приводит в первую очередь к увеличению средней скорости движения частиц,
составляющих тело. В таком случае согласно (1) увеличится средняя энергия
каждой частицы тела, а в силу аддитивности энергии
должна измениться и суммарная энергия покоящегося тела 
. Для случая вещества и гравитационного поля 
, и (44) – (45) можно записать так:
,
. (47)
Нагревание
тела приводит к изменению 
в (47), причём теплота
как некоторый вид энергии распределяется между кинетической энергией вещества и
энергией гравитационного поля.
Массу однородного шара можно определить через массу из соотношений:
, 
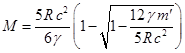. (48)
Любое
взаимодействие частиц тела между собой или с окружающей средой, которое
изменяет энергию частиц, изменяет суммарную
энергию покоящегося тела 
. При этом согласно (48) масса 
вещества шара зависит
не только от , но и от радиуса шара .
Ввиду подобия
уравнений электромагнитного и гравитационного полей, в энергии должен быть ещё
вклад от полной энергии 
электромагнитного поля
тела:
.
(49)
Для однородно заряженного по объёму и неподвижного шара с зарядом 
полная энергия
электрического поля равна:
.
Вклад в может давать и энергия
магнитного поля, если шар является намагниченным, либо если имеются
электрические токи. Мы предполагаем, что другие виды энергии (например, теплота
при нагревании) могут изменить массу тела, но не могут изменить заряд тела,
поскольку для этого нужно перенести на тело (или удалить с него) заряженные
частицы. В этом одно из отличий электромагнитного поля от гравитационного, в
дополнение к однополярности гравитационных зарядов
(которыми являются массы) и двуполярности
электромагнитных зарядов.
Массу
вещества 
в (49) можно разбить
на две части, одна из которых 
есть масса вещества
при нуле температуры по шкале Кельвина, а другая часть 
представляет собой дополнительную
массу от внутренней кинетической энергии 
, включающей в себя кинетическую энергию движения атомов и
молекул, и энергию турбулентного движения потоков вещества [8]. Если 
есть средняя скорость
частиц тела, то выполняются приблизительные соотношения: 
, 
. Как и энергии поля, мы включаем энергию 
в (49) с отрицательным
знаком:
.
(50)
Для тел,
находящихся лишь под действием собственных гравитационных и электромагнитных
полей, выполняется теорема вириала, согласно которой модуль потенциальной
энергии поля в среднем в два раза больше кинетической энергии вещества:
,
, (51)
здесь 
есть полная энергия
без учёта энергии покоя частиц тела.
Подстановка
(51) в (50) даёт приблизительное равенство:
. (52)
Рассмотрим
теперь сущность массы 
, относящейся к массе вещества тела без учёта вклада массы от
внутренней кинетической энергии и энергии макроскопических полей. В массу 
делают вклад массы от
различных видов энергии, связанных с атомами и молекулами вблизи абсолютного
нуля температуры: сильное взаимодействие, скрепляющее вещество элементарных
частиц и удерживающее нуклоны в атомных ядрах; электромагнитное взаимодействие
частиц; энергия движения электронов в атомах; энергия вращения атомов и
молекул; энергия колебаний атомов в молекулах, и т.д. В стандартной модели
предполагается, что сильное взаимодействие возникает благодаря действию глюонного поля между кварками, находящимися в адронах
(мезонах и барионах), а на лептоны сильное взаимодействие не распространяется.
Существует
также гипотеза о том, что сильное взаимодействие есть проявление сильной гравитации
на уровне элементарных частиц и атомов [9]. Поскольку гравитация имеет две
компоненты, в виде поля ускорения 
и поля кручения 
, то устойчивость нуклонов в атомных ядрах может быть описана
как баланс сил от притяжения нуклонов друг к другу за счёт 
, и отталкивания нуклонов за счёт поля кручения 
[3]. Эта же идея
применяется для описания структуры и устойчивости ряда адронов, рассматриваемых
как композиции из нуклонов и мезонов [4]. Сильная гравитация отличается от
обычной гравитации заменой гравитационной постоянной 
на постоянную сильной
гравитации 
, и действует между всеми частицами, включая лептоны. Оценку
величины можно получить из
баланса четырёх сил, действующих на электрон в атоме водорода: 1. Сила
электрического притяжения между электроном и ядром атома. 2. Сила
электрического отталкивания заряженного вещества электрона самого от себя
(электрон представляется в виде облака вокруг ядра). 3. Центростремительная
сила от вращения электрона вокруг ядра. 4. Притяжение электрона к ядру под
действием сильной гравитации. Указанные силы приблизительно равны друг другу,
так что выполняются соотношения для сил притяжения от сильной гравитации и
электрической силы [5]:
, 
м3∙кг
–1∙с –2 , (53)
где 
и 
– массы протона и
электрона соответственно,
– радиус вращения
электронного облака,
– элементарный
электрический заряд как заряд протона, равный модулю отрицательного заряда
электрона,
– электрическая
постоянная.
Другой способ
оценки 
основан на теории
подобия уровней материи и использовании коэффициентов подобия. Данные
коэффициенты определяются следующим образом: 
– коэффициент подобия
по массе (отношение массы нейтронной звезды к массе протона); 
– коэффициент подобия
по размерам (отношение радиуса нейтронной звезды к радиусу протона); 
– коэффициент подобия по
скоростям (отношение характерной скорости частиц нейтронной звезды к скорости
света как к характерной скорости вещества протона). Для постоянной сильной
гравитации получается формула: 
, причём степени коэффициентов подобия в данном равенстве соответствуют размерности
гравитационной постоянной 
согласно теории размерностей.
Если сильное
взаимодействие рассматривать как результат сильной гравитации, то основной
вклад в энергию покоя протона должна вносить положительная кинетическая энергия
его вещества и отрицательная энергия сильной гравитации (электрической энергией
протона можно пренебречь ввиду её малости). Сумма этих энергий даёт полную
энергию протона, причём в силу теоремы вириала (51) данная сумма энергий
приблизительно равна половине энергии сильной гравитации. Так как энергия
сильной гравитации отрицательна, то отрицательна и полная энергия протона.
Полную энергию протона с точностью до знака можно рассматривать как энергию
связи его вещества; энергия связи равна работе, которую надо совершить, чтобы
разнести вещество на бесконечность так, чтобы там полная энергия вещества
(потенциальная и кинетическая) стала равной нулю. По своему смыслу
положительная энергия покоя протона должна равняться энергии связи или модулю
полной энергии протона. Это даёт равенство между энергией покоя и модулем
половины энергии сильной гравитации:
,
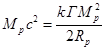(54)
где 
для случая, если бы
протон был однородным по плотности шаром радиуса 
.
Если в (54)
подставить (53), получится ещё одно равенство, позволяющее оценить радиус
протона:
, 
,
где 
есть классический
радиус электрона.
В
самосогласованной модели протона [10] находится, что в (54) радиус протона 
м, причём коэффициент 
вследствие небольшого
увеличения плотности вещества в центре протона. Одновременно с этим в
предположении, что положительный заряд распределён по объёму протона аналогично
массе, а максимальная угловая скорость вращения протона ограничена условием его
целостности в поле сильной гравитации, находится магнитный момент протона как
результат вращения заряженного вещества:
,
(55)
где 
Дж/Тл есть магнитный
момент протона,
(в случае однородной
плотности вещества и заряда протона должно быть 
).
Постоянная
сильной гравитации (53) объясняет не только энергию (54) и магнитный момент
(55) протона, но и даёт оценку константы взаимодействия двух нуклонов
посредством сильной гравитации:
,
где 
для
взаимодействия двух нуклонов, и стремится к 1 для частиц с меньшей плотностью
вещества, 
– постоянная Дирака, 
– скорость света.
Для энергии
взаимодействия двух нуклонов посредством псевдоскалярного пион-нуклонного взаимодействия,
находящихся на расстоянии 
друг от друга, и для
соответствующей константы взаимодействия при малых энергиях справедливы
формулы:
, 
,
где 
– эффективный заряд
сильного взаимодействия, 
– масса пиона.
Как видно,
константа взаимодействия 
близка к константе 
псевдоскалярного пион-нуклонного сильного взаимодействия.
То, что
энергия покоя протона связана с сильной гравитацией, вытекает также из модернизированной
теории гравитации Фатио-Лесажа [11]. В этой теории на
основе поглощения потоков гравитонов в веществе тел с передачей импульса
гравитонов веществу выводится точная формула гравитационной силы Ньютона (закон
обратных квадратов), находится плотность энергии потока гравитонов (
Дж/м3 ), сечение их взаимодействия с веществом
(
м2 ) и
другие параметры.
В теории бесконечной
вложенности материи [3], [5] показывается, что на
каждом основном уровне материи появляется соответствующий вид гравитации, на
уровне элементарных частиц это сильная гравитация, а на уровне звёзд – обычная
гравитация. Гравитация достигает максимума в самых плотных объектах – в
нуклонах и в нейтронных звёздах. В веществе земной плотности диапазон действия
сильной гравитации не превышает долей метра, и при таких размерах тел
происходит замена сильной гравитации на обычную. Это соответствует тому, что
массы и размеры объектов на различных уровнях материи нарастают в
геометрической прогрессии, причём точка замены сильной гравитации на обычную
гравитацию лежит вблизи середины диапазона масс от нуклонов до звёзд на оси
масс, взятой в логарифмическом масштабе.
Причиной
гравитации и электрических сил в рамках теории Фатио-Лесажа
полагаются потоки гравитонов, состоящие из частичек наподобие нейтрино, фотонов
и заряженных частиц. Данные потоки гравитонов, порождаемые веществом низших
уровней материи, управляют телами с помощью гравитационных и электромагнитных
сил и создают массивные объекты на более высоких уровнях материи. Эти объекты в
свою очередь на определённых стадиях своей эволюции излучают порции нейтрино,
фотонов, заряженных частиц, становящихся основой других потоков гравитонов,
действующих уже на более высоких уровнях материи. Так поля и массивные объекты
взаимно порождают друг друга на разных уровнях материи.
В описанной
картине энергия покоя протона (54) приблизительно равна модулю полной энергии
протона в собственном поле сильной гравитации (для увеличения точности следует
учесть ещё электромагнитную энергию протона), а энергия 
в (52) складывается из
энергий покоя нуклонов и электронов вещества тела с добавкой от энергии их
гравитационного и электромагнитного взаимодействия в составе вещества и
механического движения в атомах и молекулах. Следовательно, энергия тела с учётом теоремы вириала
(51) может быть сведена к половине модуля суммы энергии сильной гравитации 
и электромагнитной
энергии 
нуклонов, электронов,
атомов и молекул, участвующих в образовании энергии связи. В результате для
суммарной энергии вещества и поля некоторого покоящегося тела вместо (52) можно
записать:
.
(56)
Чтобы лучше понять смысл энергии 
, рассмотрим баланс энергии в процессе слияния вещества
вначале в элементарные частицы, затем в процессе слияния элементарных частиц в
атомы и наконец в процессе образования тела из множества атомов. Вначале
вещество находится неподвижно на бесконечности и его части друг с другом не
взаимодействуют, так что полная энергия системы равна нулю (мы не учитываем
здесь энергию покоя вещества в том его состоянии, когда оно является
раздробленным и ещё не вошло в состав элементарных частиц). Если вещество будет
сближаться под действием сильной, а также обычной гравитации, то появится
отрицательная энергия гравитационного поля 
и положительная
кинетическая энергия движения вещества 
, причём в силу закона сохранения энергии полная энергия не
должна меняться, оставаясь равной нулю. В балансе энергий следует учесть ещё
электромагнитную энергию 
и энергию 
, уходящую из системы за счёт излучения квантов поля типа
фотонов и нейтрино:
, 
. (57)
В (57) использована теорема вириала (51) для компонент полной энергии
системы 
. Согласно (57), энергия ушедшего из системы излучения с точностью до знака
равна полной энергии , то есть энергия излучения равна энергии связи
системы. Из сравнения (57) и (56) теперь видно, что суммарная энергия
вещества и поля некоторого покоящегося тела есть не что иное, как
энергия, извлекаемая из этого тела при его образовании, путём различного
излучения. Как правило в энергии учитываются только те
компоненты, которые связаны с образованием элементарных частиц, атомов и
молекулярного макроскопического вещества, а энергии связи частиц, из которых
построено вещество самих элементарных частиц, не учитываются и считаются
постоянными. Нагревание тела под действием гравитации в соответствии с (57) и
(56) приводит к увеличению энергии тела 
. Данный вывод обусловлен тем, что хотя внутренняя
кинетическая энергия тела входит в (57) с
отрицательным знаком, но изменение потенциальной энергии 
по теореме вириала
компенсирует вклад от энергии 
. Примером здесь является звезда, которая в процессе сжатия
гравитацией разогревается и ускоряет своё вращение, причём модуль гравитационной
энергии звезды увеличивается.
Согласно (56), суммарная энергия покоящегося тела , с помощью которой по формулам (47) вычисляются энергия и импульс
движущегося тела, состоит в основном из энергий двух фундаментальных полей –
гравитационного и электромагнитного, ответственных как за целостность частиц тела, так и за составленность самого тела из отдельных частиц. При этом
сильное взаимодействие частиц учитывается энергией сильной гравитации 
и электромагнитной
энергией 
.
Что касается
слабого взаимодействия, то оно полагается результатом трансформации вещества,
длительное время находящегося под воздействием фундаментальных полей. Примером
является долговременная эволюция достаточно массивной звезды с образованием
нейтронной звезды во вспышке сверхновой, когда излучается нейтринный импульс с
энергией порядка полной энергии звезды (энергия гравитации при сжатии вещества
в малую по размерам нейтронную звезду конвертируется в энергию нейтрино, в
энергию фотонного излучения и в кинетическую энергию и нагрев сбрасываемой
оболочки). На уровне элементарных частиц это соответствует процессу образования
нейтрона с излучением нейтрино.
Если от
покоящегося тела в ходе слабого взаимодействия излучаются (поглощаются телом)
нейтрино, фотоны и другие частицы, то это приводит и к изменению суммарной энергии тела . В общем случае энергия тела является функцией
времени и скорости, с которой отдельные частицы или элементы вещества
излучаются от тела или поглощаются им. В силу законов сохранения энергии и
импульса, если некоторые частицы приносят в систему энергию и импульс, то через
некоторое время они распределятся в системе и с учётом теоремы вириала могут
быть учтены через энергию и импульс фундаментальных полей. Поэтому можно
утверждать, что согласно (56) источником суммарной энергии тела, а также его
массы 
как меры инерции
являются гравитационные и электромагнитные поля, связанные с массой и с зарядами
(а также с токами) в веществе. В теории гравитации Фатио-Лесажа
предполагается, что поля, связанные с массой и с зарядами, являются следствием
взаимодействия вещества и зарядов с потоками гравитонов и мельчайших заряженных
частиц, пронизывающих пространство. Если определить суммарную массу тела в виде
, то (47) становится таким:
,
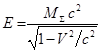. (58)
Заключение
Соотношения (58) выглядят точно так же, как (1) для малой пробной
частицы. Однако масса тела 
в (58) в полной мере
учитывает энергии полей, тогда как для массы малой частицы 
в (1) это только
предполагалось. Появление в массе 
вклада от энергии
полей произошло оттого, что мы учли энергию взаимодействия множества малых
частиц при их композиции в массивном теле. Отсюда по индукции следует
предполагать, что не только масса тела, но и масса любой изолированной малой
частицы должна определяться с учётом вклада от энергий собственных
фундаментальных полей этой частицы. Описанная концепция массы в ковариантной
теории гравитации (КТГ) подтверждается анализом функции Гамильтона [12] и
функции Лагранжа в принципе наименьшего действия [13].
Следует отметить различие результатов КТГ и общей теории относительности
(ОТО) в отношении массы и энергии. В КТГ масса
покоящегося однородного сферического тела радиуса 
выражается формулами
(46) – (49):
, (59)
где масса 
задаёт массу частей
тела без учёта потенциальной энергии полей. В результате релятивистская и
гравитационная масса тела 
при объединении частей
тела в одно целое растёт за счёт энергии поля гравитации 
, и уменьшается за счёт электрической энергии 
.
В ОТО масса тела 
в приближении слабого
поля согласно (6) определяется суммированием всех энергий с последующим
делением результата на квадрат скорости света:
. (60)
В отличие от (59), в (60) используется не масса 
, а масса 
, входящая в формулу для энергии покоя и в лагранжиан. Как
было показано в [12], для трёх масс, связанных с телом, выполняется следующее соотношение: 
. При этом 
, что так же следует из (59) и (60). На наш взгляд, причина несовпадения
(59) и (60) связана с различием позиций обеих теорий: в КТГ явным образом
существует тензор энергии-импульса гравитационного поля, входящий в лагранжиан
и вносящий свой вклад в метрику пространства-времени и в энергию-импульс
рассматриваемой системы. Это позволяет определить все три массы 
и найти их смысл,
причём масса связывается с
космологической постоянной в уравнении для метрики системы. Вместо этого в ОТО используется принцип эквивалентности,
гравитационное поле сводится к метрическому полю, соответственно, энергия и
импульс не образуют тензора и могут быть найдены лишь косвенно, через метрику
пространства-времени. В ОТО имеют смысл лишь две массы, 
и 
.
Равенство 
означает, что релятивистская и гравитационная масса
тела находится посередине
между массами и 
, и отличается от них на величину модуля потенциальной
энергии полей. Отсюда следует непротиворечивость позиций КТГ и ОТО, так как эти
теории определяют массу и энергию с различных точек зрения.
Список использованных источников
1.
Misner, Charles W.; Kip. S. Thorne
& John A. Wheeler (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0.
2. Okun L. B. Photons, Clocks, Gravity and the Concept of Mass. Nucl. Phys. B (Proc. Suppl.) 110 (2002) 151–155.
3.
Федосин С.Г. Физические теории и бесконечная вложенность материи.
Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
4.
Федосин С.Г. Комментарии к книге: Физические
теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21,
Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
5.
Федосин С.Г. Физика и философия
подобия от преонов до метагалактик. Пермь,
Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
6. Heaviside, Oliver (1888/1894), "Electromagnetic
waves, the propagation of potential, and the electromagnetic effects of a
moving charge", Electrical papers, 2, pp. 490–499.
7. Fedosin S.G. Mass, Momentum and Energy of Gravitational Field. Journal of Vectorial Relativity, Vol. 3, No. 3, September
2008, P. 30–35.
8. Fedosin
S.G. The Principle
of Proportionality of Mass and Energy: New Version. Caspian
Journal of Applied Sciences Research, 2012, Vol. 1, No 13, P. 1–15.
9. Sivaram,
C. and Sinha, K.P. Strong gravity, black holes, and hadrons. Physical Review D,
1977, Vol. 16, Issue 6, P. 1975–1978.
10. Fedosin
S.G. The radius of
the proton in the self-consistent model. vixra.org, 03 August 2012.
Accepted by Hadronic Journal.
11. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of
Vectorial Relativity, Vol. 4, No. 1, March 2009, P. 1–24.
12. Fedosin S.G. The
Hamiltonian in covariant theory of gravitation.
Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.
13. Fedosin S.G. The
Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, February 2012, Vol. 35, No. 1, P. 35–70.
Источник:
http://sergf.ru/dt.htm