Covariant theory of gravitation

Covariant theory of gravitation (CTG) is a theory of gravitation published by Sergey Fedosin in 2009. It includes extended special theory of relativity, Lorentz-invariant theory of gravitation, metric theory of relativity and Newtonian law of gravitation, and describes gravitation as a physical force acting on the particles of matter. The matter, the gravitational field, as well as other fields change such properties of wave quanta as their propagation velocity and frequency of oscillations. Since the spacetime measurements are carried out by means of waves, it follows that the observed geometrical properties of spacetime depend on the sources of energy-momentum in the form of matter and fields which are present in the reference frame. This dependence is determined by the field equations for the metric, forming a system of partial differential equations. In CTG gravitational field is a component of the general field.

Just as the [[general relativity |general theory of relativity] (GTR) and some other alternative theories of gravitation, CTG predicts change in the rate of time, the observed geometry of space, the trajectories of falling bodies, propagation of light. However, there is a difference between the predictions of GTR and CTG in the description of such effects as gravitational time dilation, gravitational redshift of the wavelength, signal delay in the gravitational field. This difference conforms to the correction containing the fourth degree of the speed of light, within the limits of which all the tests of GTR with respect to wave signals give the same results as CTG. If gravitation in GTR is the consequence of the curvature of spacetime by the sources of energy-momentum, in CTG gravitation appears as the result of the influence of gravitons on the matter within the framework of the modernized Le Sage's theory of gravitation. The fluxes of gravitons also affect the propagation of waves and hence the effective spacetime metric near the sources of energy-momentum, so in CTG geometry is secondary relative to the physics of phenomena. In weak fields and at low velocities CTG turns into LITG. Since the equations of LITG are similar to the equations of Maxwell's electrodynamics (see Maxwell-like gravitational equations) which are successfully quantized, it allows you to quantize the equations of the gravitational field of LITG in the framework of quantum gravitation.

Among the astrophysical applications, CTG as well as GTR, based on the effect of light deflection in the gravitational field, predicts the phenomenon of gravitational lensing, when there are multiple images of the same remote astronomical object. CTG assumes gravitational emission from particular accelerated massive bodies, and it can have dipole character (whereas in GTR only quadrupole and multipole emissions are always considered).

1 History
2 The transition from classical physics to CTG

2.1 Newtonian gravitation
2.2 Relativistic generalization
2.3 General relativity
2.4 Relations of CTG

3 The essence of CTG

3.1 Basic definitions and properties
3.2 The solution of equations
3.3 The principle of least action
3.4 Gravitational Aharonov-Bohm effect
3.5 The Hamiltonian

4 Consequences of the theory

4.1 The effects associated with the wave propagation
4.2 Gravitational waves
4.3 The orbital and spin effects

4.3.1 Precession of the perihelion of the orbits
4.3.2 The interaction of spins
4.3.3 The orbital Lense-Thirring effect
4.3.4 Geodetic precession
4.3.5 Pioneer anomaly

4.4 The dynamic time of the particles
4.5 The spacetime

5 Astrophysical applications

5.1 Black holes
5.2 Cosmology
5.3 The problem of mass
5.4 Relativistic uniform system
5.5 Model of gravitational equilibrium
5.6 Navier-Stokes equation

6 References
7 See also
8 External links

History

The first step in development of CTG was presenting by Fedosin the complete Lorentz-invariant theory of gravitation (LITG) in the book in 1999. ^[1] LITG is valid for inertial reference frames and describes all the gravitational effects associated with delay of gravitation propagation and with the gravitational torsion field.

In 2002 the second book by Fedosin appeared, which was devoted to the development of the theory of relativity. ^[2] In this book the axioms of extended special theory of relativity (ESTR) were formulated. In ESTR it is proved that the constancy of the speed of light in all inertial reference frames, assumed by the special theory of relativity (STR), is the result of the procedure of spacetime measurements, in which two-way propagation of light (electromagnetic wave) is always used. This leads to the averaging of the wave velocity in all directions, regardless of the true speed of light and the velocity of the reference frame, making the effective speed of light constant for each observer. According to ESTR we can consider such an isotropic reference frame in which the fluxes of gravitons have the same intensity from all sides. This reference frame can be considered fixed relative to the electrogravitational vacuum as the medium consisting of the fluxes of gravitons. In ESTR it is also shown that the theory of relativity as the theory, which allows us to recalculate the results of measurements of the coordinates, time and physical quantities from one frame to another, depends on the wave representation, that is, on the type and the properties of the wave used for spacetime measurements. This dependence is expressed in particular through the Lorentz factor of the form $~ \sqrt {1 - (V/C)^2},$ containing the effective wave velocity which depends on the properties of the medium (e.g., the refractive index of the medium), and the velocity of the reference frame as its average velocity in the period of the wave.

In his article in 2007 ^[3] Fedosin draws a deep analogy between the electromagnetic and gravitational fields, considering the similarity of their equations and the contribution that the field as the sources of energy-momentum must make in the result of determining the spacetime metric through the Hilbert-Einstein equations. Another article in 2008 ^[4] considers the violation of the equivalence principle, which is the methodological basis of GTR, as applied to the mass-energy of the gravitational field. The following article deals with the phenomenon of gravitation in the concept of gravitons (the Le Sage's theory of gravitation) in the framework of the Theory of Infinite Hierarchical Nesting of Matter. ^[5]

Based on the concepts of gravitation as the force interaction which arises from the action of gravitons and conforms to the condition of Lorentz invariance in the inertial reference frames; the conventionality of the constancy of the speed of light, following from the measurement procedure; the dependence of the results of spacetime measurements on the type and the properties of the used wave; the assumption about the same propagation speed of gravitational and electromagnetic waves, based on the model of the electrogravitational vacuum and the assumed structure of the corresponding photons, in his book in 2009 Fedosin develops CTG with the help of postulated by him axioms of the metric theory of relativity (MTR) and the covariant force equations of motion suitable for all possible reference frames. ^[6] The structure of CTG also includes the gravitational field equations of LITG, which are generalized to any reference frames by means of replacing the metric tensor of the flat Minkowski spacetime by the metric tensor of the curved spacetime, and which use the operation of covariant differentiation.

Just as in GTR, in CTG the most difficult task is finding exact solutions of the Hilbert-Einstein equations to determine the components of the metric tensor. The solution of these equations in CTG is much more complicated than in GTR, since in CTG, in contrast to GTR, the proper gravitational field of the body is taken into account, which changes the metric both inside and outside of the body. One of the exact solutions, determining the metric tensor outside a single spherical body, was found by Fedosin. ^[6] Using this solution he described in the framework of CTG the anomalous precession of the perihelion of planets, including Mercury; the deflection of relativistic particles, radio signals and the light of stars, passing close to the Sun's surface; the anomalous acceleration of "Pioneers"; the gravitational redshift; the gravitational time dilation; the effects associated with the spin, generating gravitational torsion field.

The transition from classical physics to CTG

The covariant theory of gravitation must be considered in several aspects. On the one hand, CTG is the theory of the gravitational field. On the other hand, CTG describes the interaction of the gravitational field with the matter, and the gravitational force according to Newton second law leads to acceleration of bodies. Besides, the gravitational field and other sources of energy-momentum influence the propagation of wave quanta, change their velocity, energy and frequency. This leads to the effective curvature of spacetime and to deviation of the form of the metric tensor from its value in the flat Minkowski spacetime. In turn, the metric tensor and its derivatives with respect to coordinates are involved in determining the gravitational force and the quantities, characterizing the gravitational field and the motion of bodies, from the perspective of the coordinate observer, in whose reference frame the metric is calculated.

Newtonian gravitation

According to classical mechanics the motion of physical bodies is described as the combination of free motion by inertia and some deflection from it. The reasons for the deflection are various forces acting on the body. According to Newton second law the force’s value is determined by the product of the body mass and its acceleration. According to the Newtonian law of gravitation between any two bodies the force of gravitational attraction appears which is proportional to the masses of bodies and inversely proportional to the square of the distance between them. Therefore, the trajectory of the test particle near the massive body is deflected from a straight line and the velocity changes due to the gravitational acceleration. Due to the proportionality of the gravitational force to the gravitational mass of test particles, the latter will move with the same acceleration near the massive body. This means that the free-fall trajectories of the particles depend on the initial position and the initial velocity, but not on the mass of the particles or their physical or chemical composition. This property of gravitation is defined as the principle of universality of free fall (in GTR it is called the weak equivalence principle) and is associated with the principle of equivalence of the passive gravitational and inertial masses.

The last principle can be explained as follows. Due to the equality of the gravitational acceleration, the masses of the test particles on the surface of the massive body (for example, in the laboratory on the Earth) can be determined simply by weighing (the more is the gravitation, the greater is the mass, in this case, the passive gravitational mass). Then any non-gravitational forces, which give the test particles acceleration, equal to the free fall acceleration on the Earth surface, can be equated by their effect to the corresponding gravitational forces. Because in the Newton second law for non-gravitational forces there is the so-called inertial mass, then from the equality of gravitational and non-gravitational forces and accelerations the equality follows of gravitational and inertial masses. In other words, with the appropriate calibration of forces and accelerations both masses can be equated to each other.

The Newtonian spacetime is characterized by Euclidean geometry and the independence of the rate of time on the spatial coordinates and the velocities of the bodies. Space and time depend neither on each other, nor on the material bodies, nor on the motion of these bodies. Transformations of the time and the coordinates from one frame to another are carried out by means of the Galilean transformations, in which the measurements of time and coordinates are carried out mechanically and not by means of electromagnetic waves. To synchronize the clocks in each reference frame, they are transferred from the origin of the reference frame to other points at infinitesimal velocity. It is assumed that the speed of interaction transfer by means of the force field is infinitely large.

Relativistic generalization

The emergence in the early 20th century of the special theory of relativity (STR) changed significantly the classical mechanics and the theory of gravitation as the part of it, giving them relativistic form. The Galilean transformations of classical mechanics were replaced by the Lorentz transformations. Previously independent of each other, the space and the time were combined into a single continuum, called Minkowski space. Mathematically this was expressed in the transformation of the time coordinate (multiplied by the speed of light to save the dimension) and the three-dimensional position vector of a point into the four-vector describing an event in the four-dimensional Minkowski space. Scalar and 3-vector physical quantities were combined in the 4-vectors and tensors, to obtain the value of which in different inertial reference frames the Lorentz transformations should be used (in general, in the presence of shifts and turns of reference frames Poincare transformations should be used). Due to these innovations the mechanics became consistent with electrodynamics and the concept of carrying out any spacetime measurements by means of electromagnetic waves with finite velocity of propagation. This allowed describing accurately the motion of particles even at speeds, close to the speed of light, and the phenomena with the release of energy, comparable to the rest energy.

In the theory of gravitation STR has led to the creation of the Lorentz-invariant theory of gravitation (LITG). In the inertial reference frames the force of gravitation must be transformed in a Lorentz-covariant way as any other force. If there is a physical system with a massive body and test particles, the observer can make his inertial reference frame with the help of additional forces, which balance the force of gravitation. For such observer the moving body creates not only the gravitational field strength, but also the gravitational torsion field, influencing additionally the moving test particles. The equations of LITG have relativistic form and are similar to the Maxwell equations in electrodynamics. ^[1] The Newtonian law of gravitation is a special case of LITG.

Clarification of SRT is done in the extended special theory of relativity, as it was described above in the historic section.

General relativity

Main source: Metric theory of relativity

The transition from the inertial to arbitrary reference frames means transition from special (partial) relativity of inertial reference frames to general relativity of accelerated reference frames. In case if a force is acting on the reference frame reference, the frame begins to accelerate and can no longer be considered inertial. In the presence of acceleration the relation between the physical quantities in different reference frames through the Lorentz transformation is inaccurate and requires correction. The situation is more complicated when not only on the reference frame but also to on all the matter in it the omnipresent force of gravitation is acting. The example is the isolated massive body, near which the trajectories of motion of test particles are deflected from the straight lines, having a special name – the geodesic lines.

General relativity is contained in GTR in which gravitational force and the difference of the geodesic lines from straight lines are the consequence of the curvature of spacetime near the bodies. Accordingly, the flat Minkowski space in the presence of gravitation looks like pseudo-Riemannian curved spacetime. In the free fall of particles near a massive body the velocity of the particles and the gravitational acceleration acting on them increase. Despite this, in GTR it is assumed that in the freely falling reference frame the same laws hold as in the inertial Lorentz reference frame. In this particular case general relativity differs not much from special relativity, as indicated by some experiments with the propagation of light, such as gravitational redshift. The assumption that free-falling frames are Minkowskian in GTR is called Einstein equivalence principle. It means that the falling observer with the help of internal experiments may not know whether he is falling in the uniform gravitational field, or is moving by inertia without such a field. Obviously, this assumption is only an idealization and in reality can be not satisfied. For example, in the free fall of a charged test body by changing the acceleration of the fall by the law of inverse square of the distance between the attracting center and the body, there is electromagnetic emission, proportional to the charge of the body, which is absent in the Lorentz inertial frames.

The common property of the gravitational field can be considered the slowdown of the rate of electromagnetic clock in comparison with the same clock outside the gravitational field. This follows from the reduction of the speed of light as it approaches the massive bodies. The visible sizes of bodies are also reduced in the direction of the gradient of the gravitational field. In contrast to STR, in the presence of gravitation the position vector is not a real 4-vector, and the main role is played by 4-vectors of displacement (position shift). This means the impossibility to use the integral Lorentz transformations for physical quantities. In particular, not the time and the coordinates of events are subject to transformations from one frame to another, but also the differentials of time and coordinates near these events.

In the Newtonian theory is the principle of equivalence of accelerations: if all bodies in the reference frame are given the same acceleration, then it is mechanically equivalent to the action of some uniform gravitational field, creating at all points in space the same gravitational acceleration. Einstein extended this principle to non-mechanical phenomena. Based on this principle Fedosin determined the metric inside a uniformly accelerated reference frame. ^[6] It allowed finding the relation between the coordinates and time in the accelerated and stationary reference frames. In particular it turned out that in the accelerated reference frame the transverse dimensions visually decrease, in the direction of the body’s acceleration they get longer, and at different points of the accelerated frame the time flows differently with respect to the origin of coordinates.

The main characteristic that specifies the geometry of curved spacetime is the metric tensor. It can be used to calculate the Riemann curvature tensor, as well as the connection coefficients, which determine the parallel translation of the 4-vector in curved spacetime. Since the components of the metric tensor specify the angles between the unit vectors of the coordinate axes of the reference frame, changing due to the curvature of spacetime, in general case the metric tensor is the function of time and coordinates. Due to its properties the metric tensor is included in the equations of motion of test particles and wave quanta, is taken into account in calculations of spacetime parameters and in measurements in the gravitational field, as well as in recalculation of physical quantities from one reference frame to another.

The generalization of general relativity is the metric theory of relativity (MTR), the purpose of which is the expression of general relativity of phenomena in different reference frames with the help of the metric. In MTR it is emphasized that the geometry of spacetime is not absolute, it depends on the properties of test particles and wave quanta used for the spacetime measurements and fixing the metric. The metric can depend on the velocity of test particles, and can be different for particles and wave quanta. By definition in MTR, the square of the interval is equal to zero if it is connected with two close events on the world line of test particles (wave quanta), used for spacetime measurements. In this case, the speed of test particles (wave quanta) is included in the expression for the 4-vectors and tensors, so that physical quantities are determined in the corresponding wave representation.

Theoretically, the propagation speed of light and gravitational perturbations can be different, which can give two different representations – for electromagnetic and gravitational waves, respectively. Just as in GTR, the metric in MTR is found using the corresponding equations for the metric and depends on all the sources of energy-momentum available in the reference frame. An important difference of MTR from GTR is that the gravitational field of the massive body, like any other field, becomes the source of energy-momentum and is involved in the determination of the metric. If in GTR the dependence of the metric on time and coordinates as if gives rise to gravitation, then in MTR this means that gravitation is not the consequence of the curvature of spacetime, on the contrary, gravitation itself leads to this dependence of the metric. In this case, the metric shows how under the influence of energy-momentum sources the difference of the phenomena occurs from their form in the Minkowski space, in particular due to changing of the velocity and frequency of electromagnetic waves and their deflection near massive bodies, changing of the rate of time, etc. STR, ESTR and general relativity in GTR are particular cases of MTR.

Relations of CTG

The gravitational field in CTG is considered as a vector field, and therefore, each equation of vector field will be valid for it.

CTG includes three components:

The equations of the gravitational field taken from LITG, and written in a covariant way for all reference frames.
Equation for the metric, designed to determine the components of the metric tensor through the known sources of energy-momentum.
The equations of motion of particles and wave quanta under action of the given field strengths or the sources of their energy-momentum.

The covariant gravitational field equations have the form:

$~ \nabla_n \Phi_{ik} + \nabla_i \Phi_{kn} + \nabla_k \Phi_{ni}=0,$

$~\nabla_k \Phi^{ik} = \frac {4 \pi G }{c^2_{g}} J^i ,$

where $~\Phi_{ik}$ is the gravitational tensor; $~J^i = \rho_0 u^i$ is the mass 4-current (mass current density), which generates the gravitational field; $~u^i = \frac {dx^i}{ d \tau }$ is the 4-velocity of the matter unit in the curved spacetime; is the 4-vector of displacement; $~ d \tau$ is the differential of proper time; $~\rho_0$ is the mass density in the frame at rest relative to the matter; is the gravitational constant; $~ c_{g}$ is the speed of gravitation, which is assumed to be equal to the speed of light.

In contrast to Newtonian gravitational theory, where the source of the gravitational force is assumed to be the mass of bodies, in relativistic mechanics the mass density is part of the stress-energy tensor, taking into account the energies of motion and pressure in the matter units. This tensor is used in GTR as the source of energy-momentum to determine the metric inside the matter. In CTG as the additional source the gravitational stress-energy tensor is used, which is not equal to zero even outside the matter. As a result, the equation for the metric with condition $~ c_{g}=c$ can be written as follows: ^[7]

$~ R_{ik} - \frac{1} {4 }g_{ik}R = \frac{8 \pi G \beta }{ c^4} \left( B_{ik}+ P_{ik}+ U_{ik}+ W_{ik} \right),$

where $~ R_{ik}={R^n}_{ink}$ is the Ricci tensor, which is the trace of the Riemann curvature tensor, $~ R=R_{ik}g^{ik}$ is the scalar curvature, $~ g^{ik}$ is the metric tensor, $~ \beta$ is the coefficient subject to be determined, $~ B_{ik}$ is the acceleration stress-energy tensor, $~ P_{ik}$ is the pressure stress-energy tensor, $~ U_{ik}$ is the gravitational stress-energy tensor, $~ W_{ik}$ is the stress-energy tensor of electromagnetic field.

Outside the matter, in accordance with the procedure of energy and metric gauging, both the cosmological constant and the scalar curvature, as well as tensors $~B_{{ik}}$ and $~P_{{ik}}$ become zero. ^[8] As a result, the equation for the metric is simplified:

$~R_{{ik}}={\frac {8\pi G\beta }{c^{4}}}\left(U_{{ik}}+W_{{ik}}\right).$

The equation of motion for the particles has the following form:^[9]

$~\rho _{0}{\frac {dU_{\alpha }}{d\tau }}-J^{k}\partial _{\alpha }U_{k}=\Phi _{{\alpha k}}J^{k}+F_{{\alpha k}}j^{k}+f_{{\alpha k}}J^{k}=-\nabla _{k}\left({U_{\alpha }}^{k}+{W_{\alpha }}^{k}+{P_{\alpha }}^{k}\right),\qquad (1)$

taking into account the expression for the 4-vector of force density (see the 4-force) through the covariant derivative of the stress-energy tensor of the acceleration field and through the operator of proper-time-derivative of the 4-potential $~U_{\alpha }$ of the acceleration field in the Riemannian space

$~f_{\alpha }=\nabla _{\beta }{B_{\alpha }}^{\beta }=-u_{{\alpha k}}J^{k}=\rho _{0}{\frac {DU_{\alpha }}{D\tau }}-J^{k}\nabla _{\alpha }U_{k}=\rho _{0}{\frac {dU_{\alpha }}{d\tau }}-J^{k}\partial _{\alpha }U_{k},$

where $~u_{{\alpha k}}$ is the acceleration tensor, $~\tau$ is the proper dynamic time of the particle in its rest frame, $~F_{{\alpha k}}$ is the tensor of electromagnetic field strengths, $~f_{{\alpha k}}$ is the pressure field tensor, $~j^k = \rho_{0q} u^k$ is the electromagnetic 4-current , $~\rho_{0q}$ is the density of the electric charge of the matter unit in its rest frame.

In CTG it is considered that the ordinary gravitational and electromagnetic forces are acting on the wave quanta in a special way, the fields change their velocity and frequency more. This is due to its proximity to zero of the rest mass and charge of the quanta, which leads to nulling of the densities $~\rho_0$ , $~\rho_{0q}$ , and correspondingly of the 4-vectors $~J^i = \rho_0 u^i$ and $~j^k = \rho_{0q} u^k$ for quanta, and to reduction of the action of forces on the quanta from the strengths of external fields.

Therefore, the covariant derivatives of stress-energy tensors of the gravitational and electromagnetic fields which specify the corresponding forces for quanta will be small. On the other hand, for the electromagnetic waves the interval is set to zero: , which reflects the fact that these waves are used for spacetime measurements (see also the third axiom of the metric theory of relativity).

Since for the square of the interval the relation holds: $~ds^2 \ =c^2 (d \tau)^2 = g_{ik}\ dx^{i} \ dx^{k}$ , then for the waves the differential of the proper time $~ d \tau$ is also zero. If in the equation of motion (1) we assume $~ d \tau$ to be exactly equal to zero, then in the equation uncertainty arises. It is to avoid this uncertainty by multiplying equation (1) by the squared differential $~ (d \tau)^2$ , and then dividing by the squared differential $~ (d \lambda)^2$ , where $~ \lambda$ is the time parameter which marks the position of the wave quantum in its trajectory. The right side of equation (1) vanishes because of the presence of zero multiplier in the form of the differential of the proper time $~ d \tau$ , and for the electromagnetic waves the equation of motion takes the following form:

$~ \frac{ d } {d \lambda }\left(\frac{ dx^i } {d \lambda } \right) + \Gamma^i_{ks} \frac{ dx^k } {d \lambda } \frac{ dx^s } {d \lambda } = 0. \qquad\qquad (2)$

The obtained equation of motion will have the same form as in GTR for the waves on the zero geodesic line. In deriving (2), it was taken into account that for solid-state point particles and wave quanta, the 4-potential of the acceleration field and the 4-velocity are equal to each other, $~U_{\alpha }=u_{\alpha }$ . In addition, since $~u^{k}u_{k}=c^{2}$ , the following equality holds:

$~J^{k}\partial _{\alpha }U_{k}=\rho _{0}u^{k}\partial _{\alpha }u_{k}=0.$

The essence of CTG

Basic definitions and properties

Just as GTR, CTG is the metric theory of gravitation. In contrast to LITG, satisfying only the Lorentz transformations, the equations of the gravitational field of CTG are written in covariant form and satisfy any transformations possible for the reference frames. The equations of motion for the particles and wave quanta are also covariant (covariance here means that the equations are written in the tensor form suitable for any reference frames). Before finding the physical quantities characterizing the gravitational field or the motion of test particles, it is necessary to determine the metric tensor corresponding to the distribution of the sources of energy-momentum in this reference frame. For this purpose, the appropriate equations for the metric are used.

According to the axioms of CTG the source of the gravitational field is the mass 4-current , and the field itself is characterized by the gravitational four-potential $~D_i = \left( \frac {\psi }{ c_{g}}, -\mathbf{D}\right)$ , where $~\psi$ is the scalar potential and $~\mathbf{D}$ is the vector potential. Through the 4-vector the antisymmetric gravitational tensor is determined in a covariant way:

$~\Phi_{ik}= \nabla _{i} D_{k}- \nabla_{k} D_{i} = \partial_{i} D_{k}-\partial_{k} D_{i}$ .

In turn, the tensor $~\Phi_{ik}$ allows us to determine the gravitational stress-energy tensor:

$~ U^{ik} = \frac{c^2_{g}} {4 \pi G }\left( -g^{im}\Phi_{mr}\Phi^{rk}+ \frac{1} {4} g^{ik}\Phi_{rm}\Phi^{mr}\right)$ .

In CTG gravitation is a real physical force which can be explained in the framework of the Le Sage's theory of gravitation as the result of the action of the fluxes of gravitons on the matter. Under the action of the fluxes of gravitons near massive bodies the medium, in which the wave quanta propagate, changes its properties so that the propagation velocity and the frequency of the quanta become dependent on the gravitational potential.

The gravitational field equations of CTG are written in the language of 4-vectors and tensors of second rank. Due to the correspondence principle in the weak field, these equations turn into the equations of LITG, which are valid in the special theory of relativity (STR). In turn, for the fixed bodies and with the zero vector gravitational potential, the equations of LITG can be represented as one equation for the scalar gravitational potential, which turns into the Poisson equation for the gravitational potential of classical physics.

After we could write in the explicit form the axioms of the general theory of relativity (GTR), it became possible to compare them with the systems of axioms of the metric theory of relativity (MTR) and CTG. ^[¹⁰^] ^[¹¹^] It turns out that the equations of motion of GTR are a special case of the equations of motion of CTG.

The integral field energy theorem for gravitational field in a curved space-time is as follows: ^[12]

$~-\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {D^{\alpha }\Phi _{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{D^{\alpha }\Phi _{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.$

The solution of equations

Comparison of the equations of motion for particles in CTG and GTR shows their essential difference. The equation of motion in GTR for particles in view of the electromagnetic field and its energy-momentum tensor $~W^{{ik}}$ W i k {\displaystyle ~W^{ik}} has the form:

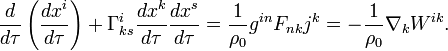
$~ \frac{ d } {d \tau }\left(\frac{ dx^i } {d \tau } \right) + \Gamma^i_{ks} \frac{ dx^k } {d \tau } \frac{ dx^s } {d \tau } = \frac {1}{\rho_0}g^{in} F_{nk} j^k = -\frac {1}{\rho_0} \nabla_k W^{ik}.$

This equation of motion is not suitable for the description of reaction propulsion. Meanwhile, if in the equation of motion of the CTG (1) the mass density $~ \rho_0$ bring in the derivative, then for the condition $~U_{\alpha }=u_{\alpha }$ for motion of solid-state particle in the equation will be the rate of change of momentum density of matter due to changes in mass density.

If this density changes with time, its derivative specifies the term for the reactive force, analogous to the well-known Meshcherskiy formula in classical mechanics for bodies of variable mass. ^[1³^] The equation of motion of CTG has the meaning of the law of conservation of energy-momentum of matter which is under the action of forces in the electromagnetic, gravitational and other fields. In contrast to this, the equation of motion of GTR reflects only equivalence principle (the acceleration of the fall is equal to the acceleration originating from the curvature of spacetime and from the non-gravitational forces), and is not connected with the law of conservation of energy-momentum. Therefore, in GTR there is no definite limiting transition to STR, i.e. to the case of weak fields, which would be based on the principle of conformity and the laws of conservation of physical quantities such as energy, momentum and angular momentum. ^[1⁴^]

In the presence of the moving matter and propagating waves the solution of the equations of CTG becomes significantly more complicated. Due to the motion of the sources of energy-momentum and their interaction with each other, the metric tensor in the considered reference frame becomes dependent on time. This leads to the change of the motion of the matter and waves, and the change of the field strengths, including due to the contribution of the changing metric tensor. As a result, the gravitational field equations, the equations for the metric and the equations of motion become coupled and must be solved simultaneously. Since these equations contain partial derivatives up to the second order, the exact solution is possible only in some special cases.

For example, the metric near the massive body, taking into account the energy-momentum of its gravitational and electromagnetic field, has been calculated by Fedosin. ^[6] ^[1⁵^] The contribution to the metric and to the total gravitational field from the test particles is considered negligible, so that the motion of the particles is regulated only by the gravitation of the massive body. The standard expression for the square of the interval between two close points in all metric theories is the following:

$~ds^2 \ = \ g_{\mu\nu}(x) \ dx^{\mu} \ dx^{\nu}.$

Substituting in this expression of the metric tensor components, found for the space outside the isolated massive body, in the four-dimensional spherical coordinates $~ct, \ r, \ \theta, \ \varphi$ gives:

$~ds^2 \ = B c^2 dt^2-\frac {1}{B} dr^2 - r^2 \left(d \theta^2 + \sin^2 \theta d \varphi^2 \right), \qquad\qquad (3)$

where $~B=(g_{{00}})_{o}=1+{\frac {GM\alpha }{rc^{2}}}-{\frac {G^{2}M^{2}\beta }{r^{2}c^{4}}}+{\frac {GQ^{2}\beta }{4\pi \varepsilon _{0}r^{2}c^{4}}}$ is the time component of the metric tensor.

The constants $~\alpha$ and $~\beta$ can not be determined by solving the equation for the metric, but their values can be found from the equations of motion of particles and waves in any given form of the metric when compared with experiments.

In the general case, for the solutions of equations it is necessary, as in GTR, to use the numerical methods, the method of small perturbations, the parameterized post-Newtonian formalism (PPN formalism) and other approximations. As a rule, the basic term of the given approximations is determined by Newtonian gravitation, and the additions arise from the general relativity of CTG (i.e., from the dependence of the results of spacetime wave measurements on any sources of energy-momentum). The feature of PPN formalism is that it allows us to compare the various alternative theories of gravitation.

The principle of least action

The equations of motion of the matter, the equations for determining the metric, the equations for the acceleration field and pressure field, gravitational and electromagnetic fields can be derived from the principle of least action.

In the case of the matter, continuously distributed throughout the space volume, the action function for the matter in the gravitational and electromagnetic fields in the covariant theory of gravitation is given by: ^[1⁶^] ^[7]

$~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}D_\mu J^\mu + \frac {c}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu} -\frac {1}{c}A_\mu j^\mu - \frac {c \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu} -$

$~-{\frac {1}{c}}U_{\mu }J^{\mu }-{\frac {c}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}-{\frac {1}{c}}\pi _{\mu }J^{\mu }-{\frac {c}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,$

where is the Lagrange function or Lagrangian, is the time differential of the used reference frame, is some coefficient, is the scalar curvature, $~\Lambda$ is the cosmological constant, which characterizes the energy density of the considered system as a whole, and therefore is the function of the system, is the speed of light as the measure of the propagation speed of the electromagnetic and gravitational interactions,

$~ A_\mu = \left( \frac {\varphi }{ c}, -\mathbf{A}\right)$ is the electromagnetic 4-potential, where $~\varphi$ is the scalar potential and $~\mathbf{A}$ is the vector potential, $~ j^\mu$ – electric four-current, $~\varepsilon_0$ is the electric constant, $~ F_{ \mu\nu}$ – electromagnetic tensor, $~ \eta$ and $~ \sigma$ are the constants of acceleration field and pressure field, respectively, $~ \pi_\mu$ – 4-potential of pressure field,

$~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3$ is the invariant 4-volume, expressed through the differential of the time coordinate ,

through the product of the differentials of the spatial coordinates, and through the square root $~\sqrt {-g}$ of the determinant of the metric tensor, taken with the negative sign.

Variations of the action function by the metric tensor, by the coordinates, by the 4-potentials of the field give the Euler-Lagrange equations as the equations of motion of the metric, matter and fields.

The action function contains terms $~-{\frac {1}{c}}D_{\mu }J^{\mu }+{\frac {c}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}$ that represent the density of the Lagrange function. With the help of these terms, a vector theory of gravity was presented in the article, ^[17] leading to the same results as the covariant theory of gravitation. Similar terms are present in the Lagrangian in the article. ^[18]

Gravitational Aharonov-Bohm effect

Основная статья: Gravitational phase shift

The analysis of the action function shows that it has the physical meaning of the function describing the change of such intrinsic properties of bodies and reference frames, as the rate of the proper time and the rate of increase of the phase angle of periodic processes. For the gravitational and electromagnetic fields difference of the clock in the weak field approximation is described by the formulas: ^[19]

$~\tau _{1}-\tau _{2}={\frac {m}{mc^{2}}}\int _{{1}}^{{2}}D_{\mu }\,dx^{\mu },\qquad \tau _{1}-\tau _{2}={\frac {q}{mc^{2}}}\int _{{1}}^{{2}}A_{\mu }\,dx^{\mu }.$

The clock 2, which measures the time $~\tau _{2}$ , is check one and the clock 1 measures the time $~\tau _{1}$ and is under the influence of additional 4-field potentials $~D_{\mu }$ or $~A_{\mu }$ . Time points 1 and 2 within the integrals indicate the beginning and the end of the field action.

The phase shift for similar processes in the field and outside it, or occurring in different states of motion is equal to:

$~\theta _{1}-\theta _{2}={\frac {m}{\hbar }}\int _{{1}}^{{2}}D_{\mu }\,dx^{\mu },\qquad \theta _{1}-\theta _{2}={\frac {q}{\hbar }}\int _{{1}}^{{2}}A_{\mu }\,dx^{\mu }.$

The phase shift, obtained due to the electromagnetic 4-potential $~A_{\mu }$ , is proved by the Aharonov-Bohm effect. The phase shift in the gravitational 4-potential is also confirmed in the papers. ^[20] ^[21] ^[^22]

From the above formulas for fixed clocks, located in the field close to each other at points 1 and 3, the next equations are following:

$~{\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}={\frac {\psi _{1}-\psi _{3}}{c^{2}}},\qquad {\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}={\frac {q(\varphi _{1}-\varphi _{3})}{mc^{2}}}.$

$~\omega _{1}-\omega _{3}={\frac {m(\psi _{1}-\psi _{3})}{\hbar }},\qquad \omega _{1}-\omega _{3}={\frac {q(\varphi _{1}-\varphi _{3})}{\hbar }}.$

This shows that the rates of the clocks at the points with different potentials of the field do not match. In the case of the gravitational field it gives gravitational time dilation.

The Hamiltonian

With the help of the Legendre transformation we can proceed from the known Lagrangian to the Hamiltonian in the four-dimensional form. In the covariant theory of gravitation the Hamiltonian is determined through the 4-velocity, the scalar potentials and the strengths of acceleration and pressure fields, of gravitational and electromagnetic fields, taking into account the metric, and for the continuously distributed matter it has the following form: ^[7]

$~H =\frac {1}{c} \int {( \rho_0 \vartheta +\rho_0 \psi+ \rho_{0q} \varphi +\rho_0 \wp ) u^0 \sqrt {-g} dx^1 dx^2 dx^3 -}$

$~ -\int {( \frac {c^2}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu}- \frac {c^2 \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu} - \frac {c^2}{16 \pi \eta} u_{ \mu\nu} u^{ \mu\nu}-\frac {c^2}{16 \pi \sigma} f_{ \mu\nu} f^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},$

where $~\vartheta$ and $~\wp$ are the scalar potentials of acceleration and pressure fields, respectively.

If we introduce the 4-vector of generalized velocity with the covariant index:

$~s_{{\mu }}=D_{{\mu }}+{\frac {\rho _{{0q}}}{\rho _{0}}}A_{{\mu }}+U_{{\mu }}+\pi _{{\mu }},$

then for the equation for the metric to hold and to perform the calibration of the Hamiltonian, the following relation is necessary:

$~\frac {c^4 \Lambda}{16 \pi G \beta } = s_{\mu } J^{\mu }.$

Since the Hamiltonian specifies the relativistic energy, it is included into the time component of the 4-vector of the Hamiltonian.

This 4-vector can be written in the contravariant form: $~H^{\mu } = \left(H{,} \frac {H}{c} \mathbf {v} \right),$ where $~\mathbf {v}$ is the velocity of center of mass of the system.

The four-momentum of the system is: $~p^{\mu } = \frac {1}{c} H^{\mu }.$

Consequences of the theory

The effects associated with the wave propagation

These effects include gravitational time dilation, gravitational redshift of the wavelength, the signal delay in the gravitational field, the deflection of light beams in the gravitational field of the Sun, and others. Since the equation of motion of CTG for the wave quanta (2) almost coincides with the corresponding equation of GTR, then the found metric coincides almost exactly. The additional difference occurs due to the contribution to the metric from the gravitational field, which is equal to $~ \frac{ G^2 M^2 \beta } {r^2 c^4 }$ and is included in $~B=g_{00}$ . With the same degree of accuracy all the effects of CTG, associated with the propagation of waves, give the same result as GTR. For the waves from the equation of motion, the effect of the beam deflection in the gravitational field and the gravitational time dilation it follows that $~\alpha=-2$ . Determination of the coefficient $~\beta$ is possible with the help of experiments on measuring the rate of time in the gravitational field.

Gravitational waves

If we consider the electromagnetic field from the moving charged particles, then it is characterized by the dipole, quadrupole, and multipole emission. As a rule, the intensity of quadrupole emission and of the subsequent multipoles is much less than the intensity of dipole emission. The similar situation for gravitational emission takes place in CTG, as the consequence of similarity of the equations of the electromagnetic and gravitational fields and the vector character of the field sources. Meanwhile, in GTR the dipole emission as such is absent, and the quadrupole and multipole gravitational emissions are associated with the tensor sources of the field and the metric oscillations propagating at the speed of light.

From the observations of the parameters of the orbits of binary neutron stars and the speeds of their approaching the change of the total energy of stars’ interaction due to the emission of gravitational waves is estimated. ^[²³^] In such frames the emission can be only quadrupole, as the consequence of stars’ rotation relative to their common center of mass. This conclusion satisfies both CTG and GTR. Although the dipole and multipole gravitational emissions can be calculated separately for each body, but in a closed frame the total dipole emission of all the bodies of the frame tends to zero.

The orbital and spin effects

In some cases, in CTG the contributions from the effective curvature of spacetime and from the forces arising from the ordinary gravitational field and gravitational torsion field are combined. This leads to different effects in the motion of test particles around massive bodies. Among them, the precession of the perihelions of the orbits, the spin and orbital Lense-Thirring effects, the geodetic precession, the effect of "Pioneers", the approaching of the orbits of bodies due to the emission of gravitational waves by them, etc.

Precession of the perihelion of the orbits

The calculation of the finite motion of the test particle around the massive body in the Kepler problem in CTG using the metric in the square of the interval (3), given above, allows us to determine the constants $~\alpha$ and $~\beta$ comparing the results with the shift of the perihelion of Mercury and other planets: $~\beta=5,$ $~\alpha \approx -\frac{ V^2} {c^2 },$ where is the quantity approximately equal to the velocity of the test particles in the orbit. These values differ from the results of GTR, where for particles and waves $~\beta=1,$ $~\alpha =-2,$ and there is no term $~ \frac{ G^2 M^2 \beta } {r^2 c^4 }$ in the metric. The difference between CTG and GTR is due to the different equations of motion for the particles (test bodies) and different metric.

The interaction of spins

During the rotation of the body there is the gravitational torsion field near it, the main term of which is the dipole component of the torsion field proportional to the spin (the proper angular momentum) of the body. In the formula for the torsion field strength there is an inverse proportional dependence on the cube of distance from the rotating body to the observation point, and on the square of the velocity of the gravitation propagation. The latter indicates that the torsion field is a relativistic effect and the consequence of the delay of the change of the gravitational field during the motion of the bodies. Since these effects are fully taken into account in STR, then to describe the interaction of two fixed rotating bodies through the torsion field, in the first approximation the formulas of LITG are sufficient, into which the formulas of CTG turn in the weak field. ^[1] ^[6]

In particular, checking of the effect was carried out on the Gravity Probe B satellite in 2004-2005 by measuring the angular velocity of the precession of the gyroscope in the torsion field of the Earth $~ \mathbf{\Omega }$ . If the gyroscope would always be located only over the North Pole of the Earth, where the spin of the Earth $~ \mathbf{L}$ and the radius vector of the distance $~ \mathbf{r}$ from the center of the Earth to the satellite are parallel, the angular velocity of the precession of the gyroscope would be equal to the maximum value:

$~\mathbf{w_{ss} } = -\frac{ \mathbf{\Omega }}{2}=\frac{G L}{2 c^2_{g} r^3} .$

Under the condition of equality of the gravitation speed and the speed of light, $~ c_{g}=c,$ for the Gravity Probe B the value $~w_{ss}$ should be approximately equal to 0,0409 arc seconds per year, or 6.28•10^–15 rad/s. The same formula for the effect is obtained in GTR, but later is was averaged over the entire orbit. ^[²⁴^] In GTR the effect of spin-spin interaction is called the Lense-Thirring spin effect or the Schiff effect, and is assumed to be the consequence of dragging of the spin inertial reference frames (frame-dragging). To describe the torsion field in GTR the so-called gravitomagnetic field is often involved, see gravitoelectromagnetism.

The orbital Lense-Thirring effect

If we give a test particle of some velocity $~ \mathbf{V}$ of the motion in its orbit around the rotating massive body with the spin $~ \mathbf{L}$ , under the action of the torsion field $~ \mathbf{\Omega}$ from this spin the moment of force arises, changing the orbital angular momentum of the particle:

$~\frac{d\mathbf{L_o} } {dt}= \mathbf{r}\times \mathbf{F},$

where the force is equal: $~\mathbf{F} = m \left( \mathbf{\Gamma } + \mathbf{V} \times \mathbf{\Omega} \right)$ , denotes the mass of the particle, $~ \mathbf{\Gamma }$ is the gravitational field strength (gravitational acceleration) from the massive body, the radius vector of the distance $~ \mathbf{r}$ is measured from the center of the rotating body to the test particle, and the orbital angular momentum of the particle equals $~\mathbf{ L_o} = m \mathbf{r} \times \mathbf{V}.$

If we express the torsion field $~ \mathbf{\Omega}$ through the spin of the body $~ \mathbf{L}$ , then for the case of circular motion we obtain the formula for the angular velocity of precession of the orbital plane of the particle relative to the direction of the body’s spin:

$~ w_o = \frac{G L} { c^2_{g} r^3 }.$

This result, as it follows from GTR and the experiments, should be doubled, because it does not take into account the spacetime metric in the reference frame of the body. In this reference frame according to CTG the gravitational field is rotating with the body and in the space there is the torsion field, which makes its contribution to the metric as the source of energy-momentum. As a result, the metric near the rotating massive body differs from the metric of a stationary body and by its form must resemble the Newman metric found in GTR for the rotating and charged body. ^[²⁵^] In the Newman metric in comparison to the Reissner metric for a stationary charged body, ^[2⁶^] there is an additional quantity associated with the rotation of the body. Therefore, in the metric of CTG near rotating massive body, taking into account the energy-momentum of the gravitational field of the body and the energy-momentum from rotation of the body, instead of the square of the interval (3) and the coefficients of the type $~\alpha$ and $~\beta$ in it there is a new form of the square of the interval and other coefficients in the metric. By choosing their values in accordance with the equation of motion of the test particle and the experiments on measuring the orbital precession, it is possible to specify the form of the metric around a rotating massive body from the perspective of CTG.

Geodetic precession

This type of precession is sometimes called the de Sitter effect or the Fokker precession. This precession occurs during the orbital motion of the test particle with the spin around the body, which may or may not rotate (the presence of rotation of the body is shown as the absolute effect and is expressed in the emergence of centripetal acceleration). The spin of the particle tends to maintain its direction in space in any motion of the particle. The parallel transfer of the spin of the particle in the orbit in the curved spacetime around the massive body leads to the fact that the spin is affected by the effective moment of force which changes its direction in space and leads to the precession with some angular velocity.

Geodetic precession also occurs in LITG, where the curvature of spacetime is not taken into account. From the perspective of the observer in the reference frame of the rotating particle, the body moves around the particle in some orbit, creating the torsion field. This torsion field acts on the spin of the particle, creating the moment of force and the corresponding spin precession of the particle. Both effects, from the spacetime curvature and from the spin-orbit interaction of torsion fields, depend on the same variables and can be added. According to GTR and to the results of experiments, ^[2⁷^] the contribution from the curvature of spacetime is two times greater than the contribution from the interaction of torsion fields. This gives the formula for the angular velocity of the precession of gyroscope, which equivalent to the rotating test particle:

$~\mathbf{w} = \frac{3 \mathbf{ V_g }\times \mathbf{\Gamma } } {2 c^2_{g}},$

where $~ \mathbf{V_g}$ is the velocity of the motion of the gyroscope in the orbit, $~ \mathbf{\Gamma }$ is the gravitational acceleration acting on the gyroscope from the massive body, $~ c_{g}$ is the speed of gravitation propagation.

For accurate calculation of geodetic precession in CTG we should use the form of the metric near the rotating massive body and with the help of it calculate the orbital motion of the rotating test particle. As in the case of the orbital Lense-Thirring effect, the indefinite coefficients in the metric are subject to redefining in comparison with the experimental results.

Pioneer anomaly

The difference of the methods of including the gravitational field into equations for the metric and the discrepancy between the equations of motion in CTG and GTR lead to the fact that in CTG it becomes possible to explain the Pioneer anomaly. ^[6] ^[2⁸^] This effect consists in the fact that in measuring the frequency of wave signals from the spacecrafts on the Earth there is difference from the predictions of GTR. According to CTG it is the consequence of the inaccuracy of the equations of GTR. CTG predicts the difference in the velocities of the spacecrafts, moving with the engines turned off and decelerated by the attraction of the Sun, is of the order of several cm/s as compared with the results of GTR in the Solar system limits. This difference in the velocities, probably also manifested as a flyby anomaly, ^[2⁹^] apparently creates the Pioneer anomaly.

The dynamic time of the particles

The equations of motion of the particles (1) and of the wave quanta (2) in CTG different from each other by their form so that the wave quanta seem not to be influenced by ordinary forces. This leads to the concept of the dynamic proper time of the moving bodies, not coinciding with the time determined by the wave (electromagnetic or gravitational) clock. The dynamic proper time in the reference frame, which is at rest relative to the particle, differs from the coordinate time of the reference frame, in which the motion of the particle is considered, due to two effects. The first is associated with the initial velocity of the particle and by its way of description is similar to the Lorentz factor in STR. The second effect results from the action of the gravitational field changing the initial velocity, and the total effect is corrected by means of the metric. In polar coordinates, the proper time of the particle is expressed through the metric coefficient and the radial and tangential velocities:

$~ d \tau = dt \sqrt {B- \frac {1}{Bc^2}\left(\frac {dr}{dt} \right)^2 - \frac {r^2}{c^2}\left(\frac {d\varphi}{dt} \right)^2 }.$

As it follows from the calculation of the motion of the relativistic particle near the massive body with the mass , in the square of the interval (3) the coefficient $~\alpha \approx \frac{ V^2_\infty } {c^2 },$ where $~ V_\infty$ is the velocity of the particle at infinity. This gives for the total deflection angle of the relativistic particle from the rectilinear motion the value $~2 \phi = \frac {4 G M} { RV^2_\infty }$ , where is the impact parameter at infinity.

For non-relativistic particles in their orbital motion $~\alpha \approx -\frac { V^2} {c^2 },$ as it was described in the section on the perihelion of the planets. Given these circumstances, with the typical orbital velocities of particles in the Solar system, the contribution from the metric into the dynamic time of the particle is small, and this time is almost entirely determined by the velocity of the particle. The proper dynamic time of particles in CTG does not have much importance, because in fact the time is always measured by electromagnetic clock. For the clock, using the waves as the working matter, the use of the equation of motion for the waves (2) gives the results similar to the results of GTR (see above the effects associated with the propagation of waves). The wave clock, except the gravitational potential, is also affected by the motion of the clock, through the values of velocity and acceleration of its motion. As it is shown in CTG, if we would use for measuring the time the wave clock, the metric of which coincides with the metric of the test body, carrying this clock (this happens in GTR due to the equivalence principle), then the time of this clock would be the proper time of the test body only in the case, when the direction of the waves in the clock and the direction of the velocity of the test body lie in the same line.

The spacetime

One of the main consequences of CTG in respect of the spacetime is the fact that in every system of bodies and test particles there is its proper spacetime. If in GTR in the static case for one massive body and one test particle the metric, which characterizes the spacetime, at each point depends only on body mass, then in CTG the situation is different. In CTG the metric depends on what is moving near the massive body, the metric is different for the wave and particle, and depends on the properties of the test particle, in particular, on its motion velocity. The dependence of the metric is realized through the coefficients $~\alpha$ and $~\beta$ , the values of which are determined by the properties of the studied bodies, particles and waves. Thus, in CTG the concept of unified spacetime for particles and waves is destroyed, which is typical of GTR. It also means the inapplicability in CTG of the equivalence principle of GTR to describe the motion of particles and waves. These consequences follow from the fact that in CTG gravitation is a real physical force and not the result of curvature of the unified spacetime as in GTR.

Changing of the concept of spacetime in CTG conforms to the idea of the scale dimension which determines the location of cosmic objects on the scale axis, and to the Theory of Infinite Hierarchical Nesting of Matter. At each basic matter level we can consider its proper gravitation (the examples are the strong gravitation at the level of atoms and the ordinary gravitation at the stars), and its proper spacetime, and the rate of time at the lowest levels of matter increases. Due to SPФ symmetry, the equations of physics remain the same if in the transition from one matter level to another, we shall make in them the corresponding transformations of such physical quantities, as mass, size and velocity. From this the relativity of spacetime follows, not only from the point of view of the method of determining its properties by definite measuring procedures, but also as the consequence of the location of the reference frame on the scale ladder of matter.

Astrophysical applications

Due to GTR in astrophysics such notions have become familiar as gravitational lensing and microlensing, detectors of gravitational waves, black holes, cosmological theories of the Universe. The phenomena associated with waves in CTG almost exactly coincide with their description in GTR. This concerns gravitational lensing, as the consequence of the deflection of light beams from the distant source by some intermediate massive object located in the way of the beams. However, the interpretation of black holes and cosmological theories in CTG is different from the standard approach.

Black holes

Main source: Black hole

The most complete picture of black holes has been developed in GTR. In this theory the proper gravitational field of the body usually is not involved in determining the metric, the metric as the object of geometric form defines gravitation and the gravitational force is the result of the spacetime geometry. However, the question – why and how does the massive body change the spacetime away from it – can not be answered by GTR. It is common for GTR and the Newtonian gravitational model – in the latter the cause of gravitation is also unknown, although there is its description as the formula for the force. As a result, in GTR neither the maximum possible degree of spacetime curvature actually realized in the nature is known, nor, correspondingly, the maximum gravitational force.

If we assume that the speed of light is the limiting speed of propagation of interactions, then this speed corresponds to the rest energy of each body, which is also proportional to body mass (see the mass–energy equivalence). Theoretically, in the formation of a black hole the mass-energy of its constituent matter should substantially decrease due to the contribution of the negative mass-energy of the gravitational field of the black hole. GTR predicts for black holes the so-called event horizon and the singularity of spacetime. It is assumed that the matter or emission, which are under the horizon of the black hole, can not get outside of the horizon and must somehow move inside the hole at relativistic velocities. From outside the black hole must look as an all-absorbing dark object with the strong gravitational field.

In CTG the description of objects with the gravitational field is made based on the modernized Le Sage's theory of gravitation, in which gravitation is generated by the fluxes of gravitons, penetrating all bodies. The calculations allow us to deduce Newton's gravitational formula and to estimate the spatial energy density of the fluxes of gravitons and their penetrating ability in the matter. ^[1] ^[5] It becomes possible to understand the origin of mass and inertia of a body, since the mass can be expressed through the power of the energy flux of gravitons, interacting with the matter of the body. ^[30]

As gravitons the relativistic particles, photons and neutrinos are assumed, generated by the matter at the lower scale levels of matter. This is consistent with the essence of the Theory of Infinite Hierarchical Nesting of Matter and electrogravitational vacuum, according to which the objects similar to stars, white dwarfs and neutron stars, create various relativistic particles and emissions at the same level of matter, and these particles and emissions with sufficiently high density of their energy lead to clustering and compression of the matter at a higher scale level. Thus gravitons as the field quanta from the scattered matter generate new compact objects, which in turn become the sources of new, more powerful field quanta. In this process the density of gravitational energy, achieved in material objects, decreases during the transition to more massive objects. In the described picture there is no place for black holes in the traditional sense. Here are some arguments against black holes:

In models of neutron stars between the nucleons (the main part of which is made up of neutrons) there are short intervals, so that the nucleons remain to be independent particles and behave almost the same as in atomic nuclei. However, the radii of black holes of stellar masses must be several times smaller than the sizes of neutron stars. In this case the nucleons must merge with each other, and the binding energy of a black hole per one nucleon must be close to the binding energy of a free nucleon (this follows from the approximate equality of the gravitational energy of the black holes and the mass-energy of its matter). For the transition of the matter into the state of a black hole this transition must be quick enough, like a supernova explosion in the formation of neutron stars, in order to overcome the nuclear forces of repulsion between the nucleons of the matter. However, the experiments with even the most energetic nucleon beams do not lead to the formation of objects of the type of black holes, only various elementary particles are formed. Consequently, for the emergence of black holes it is necessary that the force of gravitation must overcome the nuclear forces. In GTR the essence of gravitation is not revealed, nor is the maximum gravitational force found, so the conclusion of GTR about the black holes is hypothetical. From the point of view of the Theory of Infinite Hierarchical Nesting of Matter, the analogues of nucleons at the stellar level of matter are neutron stars, the collisions of which, like the collisions of nucleons in accelerators, can not lead to the formation of a black hole. This is the consequence of the significant excess of the nuclear forces between the nucleons of the neutron star over the forces of ordinary gravitation. In the gravitational model of strong interaction one of the components of the nuclear forces is strong gravitation, binding the matter of elementary particles. ^[6] The range of action of strong gravitation in the matter is small and at large distances the ordinary gravitation dominates (due to the differences in the properties of gravitons of strong gravitation and gravitons of ordinary gravitation). Because of the excess energy density of the strong gravitation over the energy density of ordinary gravitation the latter can not transfer to the matter by means of the pressure from the fluxes of gravitons enough energy for transition into the state of the black hole.
If we assume that black holes are the objects absorbing the matter and emission, and not releasing anything out, then in the Theory of Infinite Hierarchical Nesting of Matter such objects must exist at all scale levels. In Le Sage's theory, gravitons are various relativistic particles and field quanta arising in the processes of transformation of the matter of compact objects of the type of stars, and in the interaction of these objects with each other and with the scattered matter. Since the similar processes at lower scale levels take less time, then black holes at these levels would long ago have absorbed all the surrounding matter and emission. Then we would observe neither relativistic particles nor gravitons, nor the phenomenon of gravitation as such. Thus the existence of black holes at the lower scale levels contradicts their formation at the higher scale levels of matter.
At each scale level of matter only one the densest gravitationally bound object can exist which has the highest energy density of the gravitational field. For elementary particles such object is the proton, the stability of which, including the mass is estimated by a period of not less than 10²¹ years. For the level of stars such an object is assumed to be the neutron star (magnetar). If the matter fell on such objects, part of its energy would be emitted by the electromagnetic and gravitational waves, and the rest part of the mass-energy and matter would be emitted after the fall while hitting the surface and in thermonuclear flashes. This allows these objects to maintain long-term constancy of their mass. If the proton were a black hole, it would absorb mass and energy in case if the matter fell on it and would not have constant mass. This fact speaks against the existence of black holes.
In GTR black holes as the manifestation of spacetime singularities mean that they do not use the field equations and the known laws of nature. If the theory admits the existence of such objects and can not describe it, it shows either the drawback of GTR as the complete physical theory, or its contradictoriness.
There are a number of observational data that do not conform to the idea of black holes. For example, the progenitor of the neutron star CXO J164710.2-455216 is assumed a very massive star with the mass of about 40 solar masses. ^[31] Previously it was assumed that such massive stars obligatorily generate black holes at the end of their evolution. It was expected that in the globular cluster Omega Centauri there is a black hole with intermediate mass but after verification of the data its presence became unnecessary. ^[32]
There are more than a dozen massive relativistic objects, X-ray sources, which are not identified as neutron stars. The masses of these sources range from 2.5 solar masses for the XN Per to 18 solar masses for Cyg X-1. ^[³³^] According to one version, the relativistic objects in X-ray sources are black holes. But there is another point of view, according to which in these cases there are composite objects of neutron stars similar to atomic nuclei. We can explain by clusters of neutron stars the phenomena in the central parts of galaxies, attributed to black holes of large masses.

Cosmology

In the present time the main cosmological models are the models arising from the equations for the metric in GTR. As a rule it is considered that the Universe is expanding after the Big Bang which happened in the past, and the galaxies scatter from each other. Cosmological theories are meant to describe the known experimental facts, such as the redshift of the spectra of distant galaxies, homogeneity, isotropy and almost exact Euclidean character of cosmic space and of the distribution of matter on large scales, the distribution of concentrations of chemical elements in cosmos and the nucleosynthesis, the structure and the forms of large galactic systems, the isotropic cosmic microwave background radiation, the existence of dark matter, etc.

In CTG the cosmological theories on the basis of GTR are treated critically. In view of the Theory of Infinite Hierarchical Nesting of Matter and the Le Sage's theory of gravitation, the Universe can be assumed consisting of hierarchically related scale levels of matter. The observed part of the Universe, called the Metagalaxy, according to the similarity of matter levels and the SPФ symmetry is similar in size and mass to one of the objects of the metagalactic level of matter. At different scale levels of matter the gravitational quanta and gravitational fields can act which are different in energy density, penetrability and range of action. In this case, applying the conclusions of GTR with respect to ordinary gravitation to the supposedly homogeneous and infinite Universe is wrongful. Outside the Metagalaxy we can expect voids in the distribution of matter, stretching up to other similar objects. As for the experimental observations such as the redshift of the spectra of distant galaxies or the background microwave radiation, for all of them there are other explanations. For example, the redshift and the Hubble constant can be connected with the absorption of the energy of photons during their propagation in cosmological space. ^[6] ^[³⁴^] It is known that in the Big Bang theory the initial state of the Universe is assumed the singularity of spacetime. Then GTR must explain not only the emergence of the hypothetical state of singularity, but the reason for its explosive instability. For the complete and self-consistent explanation of this problem in GTR quantum gravitation is considered necessary, which has not yet been properly developed. In contrast to this in CTG neither black holes nor singularities are required, which removes a number of problems in cosmology.

In the derivation of the equations of CTG from the principle of least action we managed to show that the cosmological constant up to a constant factor determines the mass-energy density of the matter in the Universe, without taking into account the contribution of mass-energy of the macroscopic gravitational and electromagnetic fields. This means that the cosmological constant depends only on the fundamental microscopic fields acting at the level of elementary particles. ^[1⁶^]

The problem of mass

According to the principle of equivalence of mass and energy, the inertial mass of an isolated object at rest can be found through the energies of the matter and field associated with this object. To do this in GTR it is necessary to sum all kinds of energy, including the rest energy of matter, its internal energy and the energy of fields both inside and outside the object. The sum of all the energies gives the relativistic energy, which must be equal to the product of the object inertial mass and the squared speed of light. As the mass density of the object increases due to reduction of the volume under the influence of gravitation, the gravitational energy becomes more negative, which according to GTR reduces both the relativistic energy and the mass of the object, while the gravitational mass is equal to inertial mass. Thus, the star must be less massive than the sum of the masses of all the particles of which it consists.

In contrast to GTR, in CTG the other conclusions are made. This follows from the fact that the gravitational energy must be part of the relativistic energy with the negative sign due to the energy of matter in the potentials of field, and with the positive sign in relation to the energy of the field associated with field strengths. Are taken into account even the energy of matter in the acceleration field, in the pressure field and in the electromagnetic field and the energies of these fields. ^[³⁵^]

As a result there is a difference between the gravitational mass and the inertial mass of the system, so that the gravitational mass exceeds the inertial mass. Considering the relativistic energy for the case of spherically symmetrical collapse leads to four types of mass.

Gravitational mass is obtained equal to the mass , calculated as the integral of the density by volume. Inertial mass of the system taking into account the particles and fields is , and the fourth mass is found from the condition of the absence in the matter of the energy of macroscopic fields, and is obtained, for example, after sputtering of matter, and removing it to infinity. With this mass ratio is:

In GTR, the mass of the system on the principle of equivalence is equal to the gravitational mass, and for the mass ratio another expression obtained:

The article ^[36] shows that the relativistic uniform system with continuous matter distribution is characterized by five types of mass: the gauge mass is related to the cosmological constant and represents the mass-energy of the matter’s particles in the four-potentials of the system’s fields; the inertial mass ; the auxiliary mass is equal to the product of the particles’ mass density by the volume of the system; the mass $~m_{b}$ is the sum of the invariant masses (rest masses) of the system’s particles, which is equal in value to the gravitational mass $~m_{g}$ . The relation for these masses is as follows:

$~m'<M<m<m_{b}=m_{g}.$

Relativistic uniform system

Main source: Relativistic uniform system

In the gravitationally-bound uniform system, in the framework of CTG, we managed to calculate precisely the kinetic energy of particles and to find the difference from the classical virial theorem, taking into account the vector pressure field, acceleration field and electromagnetic field. ^[3⁷^] In particular, the ratio of the kinetic energy to the energy of the forces, acting on the particles, turned out to be equal to 0.6 instead of 0.5 in the classical case. Moreover, it was proved that in the equation of motion the material derivative should be used, because the velocity turned out to be the function of spatial coordinates.

An analysis of the integral theorem of generalized virial allows us to find formulas for the radial component of the velocity of typical particles of the system and for their root-mean-square speed, without using the notion of temperature. ^[3⁸^] The relation between the theorem and the cosmological constant, characterizing the physical system under consideration, is shown. The difference is explained between the kinetic energy and the energy of motion, the value of which is equal to half the sum of the Lagrangian and the Hamiltonian.

The model allows us to estimate the particles’ velocity $~v_{c}$ at the center of the sphere, the corresponding Lorentz factor $~\gamma _{c}$ , the scalar potential $~\wp _{c}$ of the pressure field; to find the relationship between the field coefficients; to express the dependences of the scalar curvature and the cosmological constant in the matter as functions of the parameters of typical particles and field potentials. ^[8] Besides, comparison of the cosmological constants inside a proton, a neutron star and in the observable Universe allows us to explain the problem of the cosmological constant arising in the Lambda-CDM model.

In article, ^[3⁹^] covariant formulas are derived for such additive integrals of system motion as momentum, energy, four-momentum, angular momentum, pseudo-tensor of angular momentum, and also for the radius-vector of the center of the system momentum. In a closed system, the integrals of motion are preserved, and the center of the momentum moves at a constant speed. The difference between the four-momentum and the integral vector, obtained by integrating the equation of motion through the energy-momentum tensors of the fields, is shown. This difference is associated with the difference of particles and fields as such.

With the help of the covariant theory of gravitation the total energy, binding energy, energy of fields, pressure energy and the potential energy of the system consisting of particles and four fields is precisely calculated in the relativistic uniform model. ^[40] A noticeable difference is shown between the obtained results and the relations for simple systems in classical mechanics, in which the acceleration field and pressure field are not taken into account or the pressure is considered to be a simple scalar quantity. In this case the inertial mass of the massive system is less than the total inertial mass of the system’s parts.

The proton, neutron star and observable Universe are very close in their properties to the relativistic uniform system. At the same time, they are extremal objects in the sense that their gravitational field significantly deviates from the form prescribed by the classical uniform system. ^[41] For a neutron star, this allows us to find the Lorentz factor for the motion of matter in the center of the star, equal to 1.04. Similarly, for the proton, the Lorentz factor in the center is 1.9. Analysis of the formula for the gravitational field allows us to explain the weakening of the field at the boundaries of the Metagalaxy, which manifests itself in the large-scale cellular structure of the Universe.

In a relativistic uniform system, the exact values of the strengths and potentials of all active fields are known. This allows us to check the field energy theorem for such a system and verify the theorem. ^[12] This theorem explains, in particular, why electrostatic energy can be calculated either through the field strength, included in the electromagnetic field tensor, or in another way, through the field potential.

In article, ^[42] within the framework of the relativistic uniform model, the components of the metric inside a spherical body were calculated in the following form:

$~(g_{{00}})_{i}=-{\frac {1}{(g_{{11}})_{i}}}=1+{\frac {8\pi G\beta r^{2}}{3c^{4}}}\left(\rho _{0}c^{2}\gamma _{c}+\rho _{0}\psi _{a}-{\frac {Gm\rho _{0}\gamma _{c}}{2a}}+\rho _{{0q}}\varphi _{a}+{\frac {q\rho _{{0q}}\gamma _{c}}{8\pi \varepsilon _{0}a}}+\rho _{0}\wp _{c}\right),$

where is the gravitational constant; $~\beta$ is the coefficient to be determined; is the radial coordinate; is the speed of light; $~\rho _{0}$ is the invariant mass density of matter particles, moving inside the body; $~\gamma _{c}$ is the Lorentz factor of particles moving at the center of body; $~\psi _{a}=-{\frac {Gm_{g}}{a}}$ is the gravitational potential at the surface of sphere with radius and gravitational mass $~m_{g}$ ; quantities $~m={\frac {4\pi a^{3}\rho _{0}}{3}}$ and $~q={\frac {4\pi a^{3}\rho _{{0q}}}{3}}$ are auxiliary values; $~\rho _{{0q}}$ is the invariant charge density of matter particles, moving inside the body; $~\varphi _{a}={\frac {q_{b}}{4\pi \varepsilon _{0}a}}$ is the electric scalar potential at the surface of sphere with total charge $~q_{b}$ ; $~\wp _{c}$ is the potential of pressure field at the center of body.

On the surface of the body, with , the component $~(g_{{00}})_{i}$ of the metric tensor inside the body must be equal to the component $~B=(g_{{00}})_{o}$ of the metric tensor outside the body in (3). This allows us to refine the expression for the metric tensor components outside the body by eliminating one unknown coefficient $~\alpha$ :

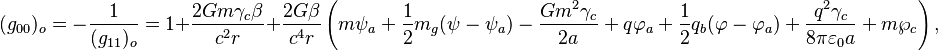
$~(g_{{00}})_{o}=-{\frac {1}{(g_{{11}})_{o}}}=1+{\frac {2Gm\gamma _{c}\beta }{c^{2}r}}+{\frac {2G\beta }{c^{4}r}}\left(m\psi _{a}+{\frac {1}{2}}m_{g}(\psi -\psi _{a})-{\frac {Gm^{2}\gamma _{c}}{2a}}+q\varphi _{a}+{\frac {1}{2}}q_{b}(\varphi -\varphi _{a})+{\frac {q^{2}\gamma _{c}}{8\pi \varepsilon _{0}a}}+m\wp _{c}\right),$

where $~\psi =-{\frac {Gm_{g}}{r}}$ is the gravitational potential outside the body; $~\varphi ={\frac {q_{b}}{4\pi \varepsilon _{0}r}}$ is the electric potential outside the body.

Model of gravitational equilibrium

This model is used to describe the internal parameters of such cosmic objects as planets and stars. In contrast to the polytropic model, relating the pressure and density by means of a certain assumed power law, the model of gravitational equilibrium is the consequence of the equations of the gravitational field, pressure field, acceleration field, electromagnetic field and other fields, acting in the matter. The approach under consideration allows us to find the distribution of the internal pressure, temperature, and other parameters. ^[43] The acceleration field coefficient η and the pressure field coefficient σ are the functions of the state of matter, and their sum is close in magnitude to the gravitational constant G. For macroscopic objects the gravitational field is the main component of the general field. ^[44] ^[45]

Navier-Stokes equation

The phenomenological Navier-Stokes equation describes the motion of the viscous fluid with regard to the dissipation field. The gravitational and electromagnetic fields are included in this equation, providing the so-called mass terms in the expressions for the acting forces. It is possible to derive the Navier-Stokes equation in a covariant way, taking into account the acceleration field and the equation of the matter’s motion in the CTG. ^[46]

The viscosity effect is described in this approach by the 4-potential of the field of energy dissipation, dissipation field tensor and dissipation stress-energy tensor. A complete set of equations is presented, which suffices to solve the problem of motion of viscous compressible and charged fluid in the gravitational and electromagnetic fields.

References

^1.0 ^1.1 ^1.2 ^1.3 Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999. ISBN 5-8131-0012-1.
Fedosin S.G. Sovremennye problemy fiziki: v poiskakh novykh printsipov. Moskva: Editorial URSS, 2002, 192 pages. ISBN 5-8360-0435-8.
Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron, Vol. 14, No. 4, pp. 385-413 (2007). http://dx.doi.org/10.5281/zenodo.891124.
Fedosin S.G. Mass, Momentum and Energy of Gravitational Field. Journal of Vectorial Relativity, Vol. 3, No. 3, pp.30-35 (2008). http://dx.doi.org/10.5281/zenodo.890899.
^5.0 ^5.1 Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009). http://dx.doi.org/10.5281/zenodo.890886.
^6.0 ^6.1 ^6.2 ^6.3 ^6.4 ^6.5 ^6.6 ^6.7 Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
^7.0 ^7.1 ^7.2 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30, (2016). http://dx.doi.org/10.5281/zenodo.889304.
^8.0 ^8.1 Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages. ISBN 978-5-9901951-1-0. (in Russian).
Fedosin S.G. The General Theory of Relativity, Metric Theory of Relativity and Covariant Theory of Gravitation: Axiomatization and Critical Analysis. International Journal of Theoretical and Applied Physics (IJTAP), Vol.4, No. I, pp. 9-26 (2014). http://dx.doi.org/10.5281/zenodo.890781.
^12.0 ^12.1 Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.
I. V. Meshchersky ("Dynamics of a point of variable mass," IV Meshchersky, St. Petersburg., 1897). Мещерский И.В. Соч.: Работы по механике переменной массы, 2 изд., М., 1952.
Gorelik, Gennady. The Problem of Conservation and the Poincare Quasigroup in General Relativity.
Fedosin S.G. The Metric Outside a Fixed Charged Body in the Covariant Theory of Gravitation. International Frontier Science Letters, Vol. 1, No. 1, pp. 41- 46 (2014). http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41.
^16.0 ^16.1 Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.
Borodikhin V.N. Vector theory of gravity. Gravit. Cosmol. Vol. 17, pp. 161-165 (2011). https://doi.org/10.1134/S0202289311020071.
Behera H., Barik N. Attractive Heaviside-Maxwellian (Vector) Gravity from Special Relativity and Quantum Field Theory. arXiv: 1709.06876v2. (2017).
Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023.
B. S. DeWitt, Superconductors and gravitational drag. Phys. Rev. Lett., Vol. 24, 1092–3 (1966).
G. Papini, Particle wave functions in weak gravitational fields. Nuovo Cimento B, Vol.v52, 136–41 (1967).
M.A. Hohensee, B. Estey, P. Hamilton, A. Zeilinger, and H. M¨uller, Force-free gravitational redshift: Proposed gravitational Aharonov-Bohm experiment, Phys. Rev. Lett. 108, 230404 (2012). doi: 10.1103/PhysRevLett.108.230404.
Weisberg J., Taylor J. Relativistic Binary Pulsar B1913+16: Thirty Years of Observation and Analysis. / Binary Radio Pulsars. ASP Conference Series, Vol. TBD, 2004, Rasio F. A., Stairs I. H. (eds.) // arXiv: astro-ph/0407149.
Yi Mao, Max Tegmark, Alan Guth, Serkan Cabi. Constraining Torsion with Gravity Probe B, arXiv:gr-qc/0608121v45, Phys. Rev. D. 76, 104029, 2007.
Newman E.T., Couch E., Chinnapared K., Exton A., Prakash A., Torrence Д. // Journ. Math. Phys., 1965, Vol. 6, P. 918.
Reissner H. – Ann. d . Phys., 1916, Bd 50, S. 106.
Straumann N. General Relativity and relativistic Astrophysics. – Springer-Verlag, Berlin, Heidelberg, New York, 1991.
Fedosin S.G. The Pioneer Anomaly in Covariant Theory of Gravitation. Canadian Journal of Physics, Vol. 93, no. 11, P. 1335-1342 (2015). http://dx.doi.org/10.1139/cjp-2015-0134.
Anderson J.D., Campbell J.K. and Nieto M.M. The Energy Transfer Process in Planetary Flybys // New Astronomy, 2007, Vol. 12, P. 383–397. – arXiv:astro-ph/0608087.
Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
Muno M. P. at al. A Neutron Star with a Massive Progenitor in Westerlund 1. – arXiv: astro-ph / 0509408 v3, 26 Jan 2006.
Jay Anderson, Roeland P. van der Marel. New Limits on an Intermediate Mass Black Hole in Omega Centauri: I. Hubble Space Telescope Photometry and Proper Motions. - arxiv:0905.0627.
Черепащук А.М. Чёрные дыры в двойных звёздных системах. – в книге «Современное естествознание. Физика элементарных частиц. Астрофизика». М.: Магистр-пресс, 2000, стр. 228–233.
Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp. 3-13 (2012). http://dx.doi.org/10.5281/zenodo.890806.
Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210.
Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8.
Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x.
Fedosin S.G. The covariant additive integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1.
Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
Fedosin S.G. The relativistic uniform model: the metric of the covariant theory of gravitation inside a body, St. Petersburg Polytechnical State University Journal. Physics and Mathematics (Научно-технические ведомости СПбГПУ. Физико-математические науки), Vol. 14, No. 3, pp.168-184 (2021). http://dx.doi.org/10.18721/JPM.14313. arXiv :2110.00342. Bibcode 2021arXiv211000342F. // О метрике ковариантной теории гравитации внутри тела в релятивистской однородной модели.
Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593.
Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.

External links

Covariant theory of gravitation in Russian

На русском языке