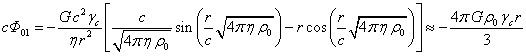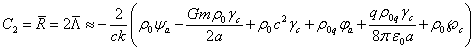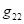Научно-технические
ведомости СПбГПУ. Физико-математические науки. Т. 14.
№ 3. С. 168-184 (2021). http://dx.doi.org/10.18721/JPM.14313.
Fedosin S.G. The relativistic uniform model: the metric of the covariant theory of gravitation inside a body, St. Petersburg Polytechnical State University Journal. Physics and Mathematics, Vol. 14, No. 3, pp.168-184 (2021).
О метрике ковариантной теории
гравитации внутри тела в релятивистской однородной модели
Федосин Сергей Григорьевич
ул. Свиязева 22-79,
город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Показывается, что сумма тензоров
энергии-импульса электромагнитного и гравитационного полей, поля
ускорений и поля давления
внутри неподвижного однородного сферического тела в рамках релятивистской
однородной модели обращается в нуль. Это обстоятельство существенно упрощает
решение уравнения для метрики в ковариантной теории гравитации (КТГ).
Компоненты метрического тензора вычисляются внутри тела и на его поверхности
сшиваются с компонентами внешнего метрического тензора. Это позволяет также
точно определить один из двух неизвестных коэффициентов в метрике за пределами
тела. Сравнение метрики КТГ с метрикой Рейсснера-Нордстрёма
в общей теории относительности показывает их различие, что является следствием
несовпадения уравнений для метрики и различного понимания сущности
космологической постоянной.
Ключевые слова: метрика; ковариантная теория гравитации; скалярная кривизна;
космологическая постоянная; релятивистская однородная система.
The
relativistic uniform model: the metric of the covariant theory of gravitation
inside a body
Sergey G. Fedosin
PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia
E-mail: fedosin@hotmail.com
It is shown that
the sum of stress-energy tensors of the electromagnetic and gravitational
fields, the acceleration field and the pressure field inside a stationary
uniform spherical body within the framework of relativistic uniform model
vanishes. This fact significantly simplifies solution of equation for the
metric in covariant theory of gravitation (CTG). The metric tensor components
are calculated inside the body, and on its surface they are combined with the
components of external metric tensor. This also allows us to exactly determine one of the two unknown coefficients in the metric outside the body.
Comparing the CTG metric and the Reissner-Nordström
metric in general theory of relativity shows their difference, which is a
consequence of difference between equations for the metric and different
understanding of essence of cosmological constant.
Keywords: metrics; covariant theory
of gravitation; scalar curvature; cosmological constant; relativistic uniform system.
1. Введение
В современной физике метрика
пространства-времени некоторой физической системы полностью определяется
соответствующим метрическим тензором. Особое значение имеет метрика в общей
теории относительности, где метрика описывает действие гравитации. В противоположность
этому, в ковариантной теории гравитации (КТГ)
гравитация является самостоятельным физическим взаимодействием. При этом
метрика КТГ требуется в основном для описания дополнительных эффектов,
связанных со взаимодействием электромагнитных волн с гравитационным полем в
процессах пространственно-временных измерений посредством этих волн.
Соответственно, вид метрики существенно зависит от используемой теории
гравитации.
Несмотря на успех общей теории
относительности в описании различных гравитационных явлений, теоретическое
обоснование этой теории до сих пор остаётся неудовлетворительным. В первую
очередь это связано с отсутствием общепризнанного тензора энергии-импульса
самого гравитационного поля, поиски которого продолжаются до настоящего времени
[1-3]. Соответственно, становится неоднозначно определёнными либо не
сохраняются энергия и импульс системы [4-6]. Среди других проблем можно
упомянуть возникающие сингулярности, необходимость трактовки космологической
постоянной,
тёмной материи, тёмной энергии и т.д. В связи с этим актуальным остаётся поиск
альтернатив общей
теории относительности, в частности, среди векторно-тензорных теорий [7-9].
Ковариантная теория гравитации (КТГ)
относится к векторным теориям и имеет точно определённый тензор энергии-импульса
гравитационного поля. За пределами неподвижного сферического тела компоненты
метрического тензора в рамках КТГ были определены в [10]. Только гравитационное
и электромагнитное поля существуют за пределами тела, соответственно лишь эти
поля оказывают здесь своё влияние на метрику пространства-времени. С помощью
этой метрики удалось вычислить эффект Пионеров, не имеющий объяснения в общей
теории относительности [11]. Формулы КТГ, описывающие гравитационное замедление
времени, гравитационное красное смещение длины волны, задержка сигнала в
гравитационном поле, приводят к тем же результатам, что и общая теория относительности [12].
Далее мы будем вычислять метрику КТГ
внутри тела сферической формы. При наличии вещества следует учесть поле
давления, которое рассматривается нами в ковариантной форме как векторное поле.
Аналогично, для вычисления энергии и импульса вещества, и его вклада в
уравнение для метрики используется концепция векторного поля ускорений [13-14].
Именно представление этих полей в виде векторных полей позволило найти
ковариантное выражение для уравнения Навье-Стокса [15]. В отличие от этого, в
общей теории относительности поле давления и поле ускорений практически всегда
рассматриваются как простые скалярные поля. Следовательно можно считать, что
КТГ более точно представляет вклад полей в энергию и импульс, а также и в
метрику системы.
С целью упрощения решения поставленной
задачи будем считать, что вещество тела движется хаотически в объёме
сферической формы, удерживаемое от распада гравитацией. Сила гравитация в таких
макроскопических объектах, как планеты и звёзды, настолько сильна, что её уже
достаточно для формирования сферической формы данных объектов. Данной силе противодействуют сила давления в
веществе и сила от поля ускорений. Одним из проявлений силы от поля ускорений
является центробежная сила, возникающая от той компоненты скорости частиц,
которая перпендикулярна радиус-вектору частиц. Мы можем взять в учёт ещё
электромагнитное поле и соответствующую силу, как правило приводящую к расталкиванию
заряженного вещества в случае избыточного заряда одного знака. Будем считать
также, что рассматриваемая физическая система представляет собой релятивистскую
однородную систему, в которой распределения массы и заряда подобны друг другу.
Это позволит использовать найденные ранее выражения для потенциалов и
напряжённостей полей.
Необходимость определения метрики
внутри вещества связана с тем, что сравнение выражений для компонент
метрического тензора внутри и за пределами вещества позволяет однозначно
определить один из неизвестных коэффициентов во внешней метрике. В результате
мы получаем более точное выражение для метрики КТГ, пригодное для решения более
сложных задач и рассмотрения малых гравитационных эффектов.
2. Уравнение для метрики
Использование принципа наименьшего
действия приводит к следующему уравнению для метрики в КТГ [14]:
. (1)
Здесь 
– скорость света; 
– постоянная, входящая в лагранжиан в
членах со скалярной кривизной 
и с космологической
постоянной 
; 
– тензор Риччи со смешанными индексами;
– единичный тензор или символ
Кронекера;
, 
, 
и 
– тензоры энергии-импульса
гравитационного и электромагнитного полей, поля ускорений и поля давления,
соответственно.
Как было показано в [16], все величины
в (1) должны быть усреднены по объёму типичных частиц системы, если (1)
используется для отыскания метрики внутри тела. Будем считать далее, что в (1)
уже проведено такое усреднение. Другим выводом в [16] является то, что в рамках
релятивистской однородной модели скалярная кривизна внутри неподвижного
тела с постоянной релятивистски-инвариантной плотностью массы и заряда является
некоторой постоянной величиной 
. При этом в КТГ выполняется соотношение 
, где 
обозначает усреднённую
космологическую постоянную для вещества внутри тела.
Действуя как в [10], будем использовать
сферические координаты 
, 
, 
, 
, связанные с декартовыми координатами соотношениями: 
, 
, 
. Для статической метрики стандартной формой метрического
тензора сферического однородного тела является следующее:
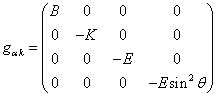, (2)
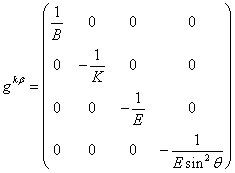, (3)
где 
являются функциями
только радиальной координаты 
и не зависят от
угловых переменных, и имеются четыре ненулевые компоненты метрического тензора 
, 
, 
, 
.
По определению, коэффициенты
Кристоффеля 
выражаются через
метрический тензор и его производные:
. (4)
Если обозначить производные по радиусу 
штрихами, то ненулевые
коэффициенты Кристоффеля, выраженные через функции 
в метрическом тензоре
(2) и (3), согласно (4) равны:
, 
, 
. (5)
С помощью (5) вычислим компоненты
тензора Риччи с ковариантными индексами по стандартной формуле:
.
Это даёт четыре ненулевые компоненты:
, 
,
, 
.
(6)
Уравнение (1) содержит компоненты
тензора Риччи со смешанными индексами, которые можно найти путём умножения
компонент этого тензора с ковариантными индексами на метрический тензор по
формуле: 
. С помощью (6) и (3) находим:
, 
,
,
.
(7)
Скалярную кривизну с помощью (6) и (3)
вычислим следующим образом:
. (8)
3. Тензоры полей
Тензоры энергии-импульса
гравитационного поля [17-18], электромагнитного поля, поля ускорений и поля
давления [14], находящиеся в правой части уравнения для метрики (1), можно
выразить так
,
.
,
. (9)
В (9) 
, 
, 
и 
– тензоры гравитационного и электромагнитного
полей, поля ускорений и поля давления, соответственно; 
– гравитационная постоянная; 
– электрическая постоянная; 
– постоянная поля ускорений; 
– постоянная поля давления.
Тензоры энергии-импульса в (9) были
выведены из принципа наименьшего действия в предположении, что все имеющиеся в
рассматриваемой системе физические поля описываются как векторные поля, имеющие
свои собственные 4-потенциалы [13]. Благодаря тому, что тензоры полей имеют
одну и ту же форму, все поля удалось объединить в единое общее поле [19-20].
Выразим 4-потенциалы полей через
соответствующие скалярные и векторные потенциалы этих полей: 
для гравитационного
поля, 
для электромагнитного поля, 
для поля ускорений, 
для поля давления.
Гравитационный тензор определяется как 4-ротор
от 4-потенциала [17]. Аналогично вычисляется электромагнитный тензор, тензор
ускорений и тензор поля давления [14]:
, 
.
, 
.
(10)
В рассматриваемой системе векторные
потенциалы 
, 
, 
и 
всех полей близки к
нулю из-за хаотичного движения частиц вещества. Это связано с тем, что
векторные потенциалы отдельных частиц направлены вдоль скоростей частиц и
потому каждый раз изменяются в результате взаимодействий. Глобальный векторный
потенциал каждого поля внутри тела вычисляется как векторная сумма
соответствующих векторных потенциалов частиц. В каждый момент времени
большинство частиц системы имеют разнонаправленные скорости и векторные
потенциалы, так что в среднем векторная сумма этих потенциалов стремится к
нулю. Чем больше частиц в системе, тем точнее выполняется равенство нулю
глобальных векторных потенциалов полей. Мы не будем также учитывать собственные
векторные потенциалы отдельных частиц. Как было показано в [21], благодаря всем
этим потенциалам возникает энергия движения частиц, приблизительно равная их
кинетической энергии. Таким образом неточность, возникающая от приравнивания к
нулю векторных потенциалов , 
, 
и 
, не превышает неточности в том случае, когда в энергии
системы берётся лишь энергия покоя и не учитывается кинетическая энергия
частиц.
Что касается скалярных потенциалов
полей 
, 
, 
и 
, то в статическом случае для неподвижного сферического тела
они должны зависеть только от текущего радиуса 
и не зависеть ни от
времени, ни от угловых переменных.
Считая, что 
и пренебрегая вкладом
векторного потенциала 
, в сферических координатах 
, 
, 
, 
из (10) и (3) находим
ненулевые компоненты гравитационного тензора:
. (11)
В (11) величина 
в сферических
координатах есть проекция векторного потенциала на радиальную компоненту
четырёхмерной системы координат. При этом величина 
представляет собой проекцию
напряжённости гравитационного поля на радиальную компоненту системы координат.
Ненулевые компоненты электромагнитного
тензора, тензора ускорений и тензора поля давления получаются аналогично (11):
. 
.
. (12)
В пространстве-времени Минковского
справедлива специальная теория относительности, так что потенциалы и
напряжённости полей могут быть вычислены точно. Для случая релятивистской
однородной модели напряжённости полей, входящие в компоненты тензоров полей
внутри сферического тела, в статическом случае имеют следующий вид [22]:
,
,
,
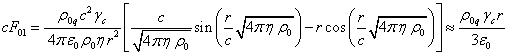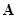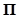
(13)
В (13) 
есть фактор Лоренца
типичных частиц, находящихся в движении в центре тела; 
и 
обозначают
соответственно инвариантные плотности массы и заряда типичных частиц. Данные
плотности массы и заряда получаются в системах отсчёта, которые являются
сопутствующими для частиц. Из (10-13) следует, что тензоры полей внутри тела
пропорциональны друг другу:
. (14)
Просуммируем все тензоры
энергии-импульса в (9) и используем (14):
.
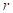(15)
Как было найдено в [23] из уравнения движения
частиц, и в [24] из обобщённой теоремы Пойнтинга, для суммы коэффициентов полей
внутри тела выполняется условие:
. (16)
Подставляя условие (16) в (15), мы
обнаруживаем, что сумма тензоров энергии-импульса внутри тела, находящегося в
равновесии, обращается в нуль:
.
(17)
Соотношение (17) было также выведено в
[24]. Изменится ли результат (17), если рассматривать ситуацию в искривлённом
пространстве-времени? В рассматриваемой физической системе в виде сферического тела
метрика пространства-времени статична и зависит только от радиальной
координаты. Так как векторные потенциалы полей полагаются равными нулю, тензор
каждого поля содержит лишь две ненулевые компоненты, одинаковые по модулю. Учёт
метрики искривлённого пространства-времени приводит к тому, что компоненты
тензоров каждого поля в (13) должны быть умножены на некоторую одну и ту же
функцию 
, зависящую от компонент метрического тензора. Как и
компоненты метрического тензора, эта функция будет зависеть лишь от радиальной
координаты. При этом в плоском пространстве-времени Минковского данная функция
должна быть равной единице, 
, чтобы
выполнялось (13), в котором нет .
Действительно, уравнения для вычисления
тензоров всех векторных полей совпадают друг с другом по форме согласно [13], [18], [25], так что в релятивистcкой однородной модели
при неизменной плотности массы 
и плотности заряда 
тензоры полей могут отличаться друг от
друга лишь постоянными коэффициентами. Поэтому, если тензор каждого поля,
найденный в пространстве-времени Минковского, умножить на одну и ту же функцию для нахождения этого же тензора в
искривлённом пространстве-времени, соотношение (14) не изменится, а в правой
части (15) появится дополнительный множитель 
.
Так как условие (16) выполняется всегда, то в рассматриваемой системе сумма
тензоров энергии-импульса в (15) и (17) будет равна нулю и в искривлённом
пространстве-времени.
4. Вычисление метрики внутри тела
Уравнение для метрики (1) с учётом (17) существенно упрощается:
.
Подставляя сюда (7) и (8), получаем три уравнения:
. (18)
. (19)
. (20)
Подстановка
(20) в (18) и в (19) даёт одно и то же уравнение:
, или 
.
(21)
Если
вычесть уравнение (18) из (19), то снова получится (21). Уравнение (21) легко
интегрируется, так как каждый член представляет собой производную натурального
логарифма от соответствующей функции:
,
(22)
где
есть некоторая
константа.
Используем
теперь полученное в [16] условие, согласно которому скалярная кривизна внутри
тела должна быть постоянной величиной, 
. С помощью (8) находим:
.
(23)
Сумма
(23) и (18) даёт:
.
Сравнивая
это выражение с (20), получим:
.
Подставим
сюда значение 
согласно (22):
.
(24)
Далее
нам понадобится 
из (22) и
отношение 
из (21):
, 
. (25)
Подставим
(25) в (20):
. (26)
Уравнения
(24) и (26) составляют вместе систему из двух дифференциальных уравнений для
двух функций 
и 
. Непосредственной подстановкой можно убедиться в том, что
система этих уравнений имеет следующее решение: 
, 
.
Действительно,
в слабом гравитационном поле, когда искривлённое пространство-время переходит в
пространство-время Минковского, в сферических координатах должно быть 
, 
. Для того, чтобы функция не была бесконечной
большой в центре при 
, константа 
должна быть равной
нулю. Из условия 
следует, что 
, и из (22) получается равенство 
. Кроме этого, постоянная 
должна быть достаточно
малой величиной. В итоге для компонент метрического тензора можно записать:
, 
.
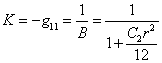(27)
Константа
в (27)
представляет собой усреднённое по объёму типичной частицы значение скалярной
кривизны, постоянное внутри тела, так что .
В
[16] было найдено соотношение для усреднённой по объёму типичной частицы
значение космологической постоянной 
:
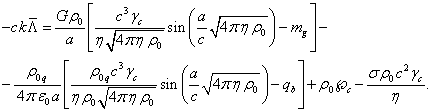
Раскладывая
синус по правилу 
, с учётом (16) находим:
.
Здесь
,
(29)
где
– некоторая константа порядка единицы; 
есть скалярный потенциал гравитационного поля на
поверхности тела при 
; 
– скалярный потенциал электрического поля; 
– радиус тела; 
– гравитационная масса тела; 
– полный заряд тела; 
–
фактор Лоренца частиц в центре тела; 
– потенциал поля давления в центре сферы;
масса 
и заряд 
являются
вспомогательными величинами.
В
скобке в правой части (28) находится сумма объёмных плотностей энергии частиц в
скалярных потенциалах полей – первый и второй члены возникают от
гравитационного поля, третий член от поля ускорений, четвёртый и пятый члены от
электрического поля и шестой член от поля давления. Самым большим является
третий член, пропорциональный плотности энергии покоя тела. Если учитывать
только этот член, то в первом приближении константа 
будет равна:
.
5. Сравнение компонент метрического тензора внутри и снаружи тела
При текущий радиус достигает поверхности
сферического тела, и здесь внутренняя метрика становится равной внешней
метрике. Это означает, что при мы можем приравнять
компоненты соответствующих метрических тензоров. Согласно [10],
компоненты метрического тензора за пределами тела в
ковариантной теории гравитации равны:
,
,
, 
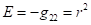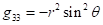. (30)
Из
сравнения (30) и (27) видно, что компоненты 
и 
совпадают как внутри,
так и снаружи тела.
Приравнивая
в (27) и (30) при
условии , с учётом (28) и (29), находим постоянную 
:
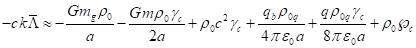. (31)
Согласно
[22], гравитационная масса 
тела и
полный электрический заряд определяются
так:
.
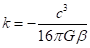(32)
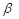
Поскольку
, то оказывается, что 
, а также 
.
Подставим
(31) в (30) в выражение для и учтём (29):
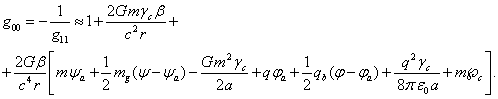(33)
В
данном выражении 
и 
обозначают скалярные
потенциалы гравитационного и электрического полей за пределами тела,
соответственно.
Можно
ещё уточнить значения величин 
и . В [21] было найдено выражение для квадрата скоростей частиц
в центре сферического
тела, с помощью которого можно оценить значение фактора Лоренца в (33):
.
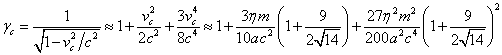Согласно [26], скалярный потенциал поля давления в центре тела приблизительно равен:
,
при этом постоянная поля ускорений 
и постоянная поля давления 
выражаются формулами:
, 
.
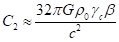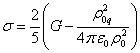В
(33) мы видим сложную структуру компонент метрического тензора, в которых
появляются добавочные члены по сравнению с метрикой пространства-времени
Минковского, где в сферических координатах 
. Основной добавкой в (33) является член 
, и если учесть (32), то эта добавка станет
приблизительно равной 
.
Вторая по значимости добавка включает в себя квадратную скобку в (33), которая по порядку величины задаёт энергию гравитационного и электрического полей и поля давления. В данной скобке также можно воспользоваться приблизительной связью масс в выражении (32). Всё это для компонент метрического тензора за пределами тела приводит к следующему:
.
(34)
В
(34) в правой части в круглой скобке находятся величины с размерностью энергии.
Для больших космических тел основной величиной здесь является отрицательная
энергия, связанная с гравитацией. В этом случае видно, что третий член,
содержащий в знаменателе 
, отличатся знаком от второго члена, содержащего в
знаменателе 
.
6. Сравнение с метрикой общей теории относительности
Для сравнения с компонентами метрического тензора (30) и (34) рассмотрим метрику Рейсснера-Нордстрёма в сферических координатах, описывающую статическое гравитационное поле вокруг заряженного сферического тела в общей теории относительности. Используем для этого наши обозначения для потенциалов полей:
, 
,
,
.
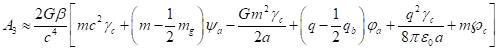(35)
Как видно, второй и третий члены в компоненте 
в метрике Рейсснера-Нордстрёма (35) существенно отличаются от соответствующих членов в
компоненте 
в метрике КТГ (34) за пределами тела. Мы видим например, что метрика
(35) никак не отражает энергию поля давления внутри тела, тогда как в (34)
энергия 
связана с полем давления и вносит свой вклад в метрику. С учётом
(28), энергия определяет также метрику
(27) внутри тела.
Указанное
различие вида метрики в обеих теориях связано с различием уравнений для
определения метрики. Если в КТГ используется уравнение (1), то в общей теории
относительности уравнение для метрики с космологической постоянной 
, в веществе с тензором энергии-импульса 
имеет следующий вид:
. (36)
Согласно подходу общей
теории относительности, действие гравитации должно описываться метрическим
тензором, и потому 
не включает в себя
тензор энергии-импульса гравитационного поля. За пределами заряженного тела нет
вещества и поля давления, в правой части (36) остаётся лишь электромагнитное
поле, так что будет 
. Как правило, в (36) пренебрегают членом с космологической
постоянной ввиду её малости, и
тогда получают решение для метрики (35).
Поскольку
в КТГ космологическая постоянная учитывается полностью, у нас получается, что
решение (27) с учётом (28) для метрики КТГ внутри тела, и решение (33) снаружи
тела являются более точными и информативными, чем решение (35) в метрике Рейсснера-Нордстрёма. При этом внутри тела космологическая постоянная 
в КТГ не равна нулю и пропорциональна потенциалам всех
действующих полей. Если в (28) учесть только основной член с плотностью энергии
покоя, то с учётом соотношения (29) можно оценить величину :
.
(37)
Если подставить сюда среднюю плотность массы вещества
космического пространства наблюдаемой Вселенной, получится значение 
м–2. Малость
космологической постоянной 
внутри космических тел
связана с большим по величине множителем 
согласно (29),
появляющимся в (37).
Напомним
в этой связи, что вопрос с космологической постоянной в общей теории
относительности до сих пор не урегулирован однозначно [27], особенно в
отношении корреляции с вакуумной энергией. Здесь имеется в виду, что очень
большая по величине вакуумная энергия почему-то очень слабо проявляет себя в
отношении вклада в метрику и в малую по величине космологическую постоянную.
В
КТГ чем больше плотность массы в (37), тем больше становится 
внутри тела. Если же
размазать по пространству вещество всех космических тел, то плотность массы
будет очень малой, что и приводит к незначительной по величине м–2.
Следует обратить ещё внимание на то, что в КТГ космологическая постоянная за
пределами тела полагается равной нулю в силу её калибровки [16].
Внутри же тел, и в том числе внутри наблюдаемой Вселенной как некоторого
глобального тела, имеет некоторое
определённое значение. В приближении релятивистской однородной модели тела, определяется в (28).
В противоположность этому, в общей теории относительности в (36) допускается не нулевое значение космологической постоянной за пределами тела. Последнее следует из возможности влияния нулевой энергии вакуума на метрику через космологическую постоянную.
7. Заключение
В
разделе 3 мы показали, что сумма тензоров энергии-импульса всех четырёх полей
внутри тела равна нулю. С учётом этого были вычислены компоненты метрического
тензора (27) как функции текущего радиуса. В результате на поверхности тела при
стало возможным
сравнить метрику внутри и снаружи тела и уточнить неизвестный коэффициент 
во внешней метрике
(30).
Представленные
в (30) компоненты 
и 
метрического тензора
за пределами неподвижного сферического тела в ковариантной теории гравитации
(КТГ) были конкретизированы нами в (33) и (34). При этом выясняется, что данные
компоненты являются функциями от скалярных потенциалов всех полей, так что
например поле давления внутри тела также влияет на метрику за пределами тела.
Однако основной вклад в метрику делает скалярный потенциал гравитационного поля
. По-видимому это связано с тем, что в
выражении для скалярного потенциала 
находится
гравитационная масса 
, характеризующая источник поля и силу
гравитации. Одновременно с этим релятивистская энергия пропорциональна инертной
массе 
, причём для внешнего наблюдателя масса
есть масса покоя и
характеризует систему в отношении действующих на неё сил.
Обе указанные массы отличаются друг от друга на массу-энергию связи частиц
посредством полей [26]. Что касается
электромагнитного поля, то его вклад оказывается вторичным. Заряд тела лишь
косвенно входит в массу покоя тела и не входит прямо в гравитационную массу. В
нейтральных телах в (34) исчезают потенциалы электрического поля. Таким
образом, гравитационное поле является основным фактором, отличающим метрику
искривлённого пространства-времени от метрики плоского пространства-времени
Минковского.
Наши
расчёты позволили вычислить метрику КТГ внутри тела и уточнить метрику снаружи
тела, однако в компонентах метрического тензора остался ещё один неизвестный
подгоночный коэффициент 
. Его появление связано с тем предположением, что коэффициент
в (29) имеет точное значение, так что коэффициент
призван обеспечить правильное значение
метрики. Величина коэффициента может быть определена из
гравитационных экспериментов, в которых необходимо учитывать метрику
пространства-времени.
Список использованных источников
1. M. Sharif and Tasnim Fatima. Energy-Momentum
Distribution: A Crucial Problem in General Relativity. Int. J. Mod. Phys. A. Vol. 20
(18), 4309 (2005). DOI: 10.1142/S0217751X05020793.
2. Cooperstock F. I. and Sarracino R. S. The localization of energy in general relativity. Journal of Physics A: Mathematical and General. Vol. 11, No. 5, 877 (1978).
3. Rüster S.B. The Fundamental Conservation Law in the Theory of General
Relativity: an unconventional approach is feasible and correct? Parana Journal
of Science and Education, Vol. 6, No. 9, pp. 1-11 (2020). http://tiny.cc/PJSE24476153v6i9p001-011.
4. Денисов,
В. И.; Логунов А. А. Инертная
масса, определенная в общей теории относительности, не имеет физического смысла.
ТМФ, 1982, том 51, номер 2, 163-170; Denisov V. I., Logunov A. A. The inertial mass defined in the general theory of relativity has no physical meaning. Theoretical and Mathematical
Physics, Volume 51, Issue 2, pp. 421-426 (1982). http://dx.doi.org/10.1007/BF01036205.
5. Khrapko, R. I. The Truth about the Energy-Momentum
Tensor and Pseudotensor. ISSN 0202-2893, Gravitation and Cosmology,
Vol. 20, No. 4, pp. 264-273 (2014). Pleiades Publishing, Ltd., 2014. http://dx.doi.org/10.1134/S0202289314040082; Храпко Р.И. Правда
о тензоре и псевдотензоре энергии-импульса.
6. Дирак П. А. М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с. Dirac P. A. M. General Theory of Relativity (1975), Princeton University Press, quick presentation of the bare essentials of GTR. ISBN 0-691-01146-X.
7. Roberto Dale and Diego Sáez. Testing
vector-tensor gravity with current cosmological observations. Journal of
Physics Conference Series 600(1):012044 (2015). http://dx.doi.org/10.1088/1742-6596/600/1/012044.
8. Davood Momeni, Mir Faizal, Kairat Myrzakulov, Ratbay Myrzakulov. Compact stars in vector–tensor-Horndeski theory of gravity. Eur. Phys. J. C. Vol. 77, No. 1, Article No 37 (2017). DOI https://doi.org/10.1140/epjc/s10052-017-4606-2.
9. Lavinia Heisenberg and Matthias Bartelmann.
Kinetic field theory applied to vector-tensor gravity. Physics Letters B, Vol.
796, pp. 59-64 (2019). https://doi.org/10.1016/j.physletb.2019.07.004.
10.
Fedosin S.G. The Metric Outside a Fixed Charged
Body in the Covariant Theory of Gravitation. International Frontier
Science Letters, Vol. 1,
No. 1, pp. 41-46 (2014). http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41;
Метрика за пределами неподвижного заряженного
тела в ковариантной теории гравитации.
11. Fedosin S.G. The Pioneer Anomaly in Covariant
Theory of Gravitation.
Canadian Journal of Physics, Vol. 93, No. 11, pp. 1335-1342 (2015). http://dx.doi.org/10.1139/cjp-2015-0134. // Эффект "Пионера"
в ковариантной теории гравитации.
12. Sergey Fedosin, The physical theories and infinite
hierarchical nesting of matter, Volume 2, LAP LAMBERT Academic Publishing, pages: 420, ISBN-13:
978-3-659-71511-2. (2015).
13. Fedosin S.G.
The
procedure of finding the stress-energy tensor and vector field equations of any
form.
Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). doi:10.12988/astp.2014.47101; Процедура для нахождения
тензора энергии-импульса и уравнений векторного поля любого вида.
14. Fedosin S.G. About the
cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304;
О космологической постоянной, поле ускорения, поле давления и об энергии.
15. Fedosin S.G. Four-Dimensional Equation of
Motion for Viscous Compressible and Charged Fluid with Regard to the
Acceleration Field, Pressure Field and Dissipation Field. International
Journal of Thermodynamics, Vol. 18, No. 1, pp. 13-24 (2015). doi: 10.5541/ijot.5000034003; Четырёхмерное
уравнение движения вязкого сжимаемого вещества с
учётом поля ускорений, поля давления и поля диссипации.
16.
Fedosin S.G. Energy and metric gauging in the covariant theory of
gravitation. Aksaray University Journal of Science and
Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947;
Калибровка энергии и метрики в ковариантной
теории гравитации .
17.
Федосин С.Г. Физика и философия
подобия от преонов до метагалактик. Пермь: Стиль-МГ, 1999, 544 стр., Табл.66,
Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
18.
Fedosin S.G. The Principle of Least Action in
Covariant Theory of Gravitation. Hadronic
Journal, Vol. 35, No. 1, pp.
35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804;
Принцип наименьшего действия в ковариантной
теории гравитации.
19.
Fedosin S.G. The Concept of the General
Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; Концепция
общего силового векторного поля.
20.
Fedosin S.G. Two components of the macroscopic
general field. Reports
in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025; Две компоненты макроскопического общего поля.
21. Fedosin S.G.
The virial theorem and the
kinetic energy of particles of a macroscopic system in the general field
concept. Continuum Mechanics and Thermodynamics, Vol. 29,
Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и
кинетическая энергия частиц макроскопической системы в
концепции общего поля.
22.
Fedosin S.G. Relativistic Energy and Mass in the
Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская
энергия и масса в пределе слабого поля.
23.
Fedosin S.G.
Estimation of the physical parameters of planets and stars in the gravitational
equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров
планет и звёзд в модели гравитационного равновесия.
24.
Fedosin S.G. The generalized Poynting theorem
for the general field and solution of the 4/3 problem. International Frontier
Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19; Обобщённая
теорема Пойнтинга для
общего поля и
решение проблемы 4/3.
25. Федосин С. Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
26. Fedosin S.G. The binding energy and
the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp.
46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
27. Martin J. Everything you always wanted to know about the cosmological
constant problem (but were afraid to ask). Comptes Rendus Physique, Vol. 13, Issue 6, pp. 566-665 (2012). http://dx.doi.org/10.1016/j.crhy.2012.04.00.
Источник: http://sergf.ru/ru.htm