На русском языке

Gravitational phase shift

From Wikiversity

Gravitational phase shift is a phenomenon, in which the components of gravitational four-potential and gravitational tensor independently change the phase and frequency of periodic processes, as well as the time flow rate. This phenomenon can be detected by comparing results of two experiments, conducted in gravitational field with different potentials or mismatching field strengths.

Historically, the first predicted effects were gravitational time dilation and gravitational redshift. [1]  In the first effect, deceleration of clock rate is detected, when placed in gravitational field, which can be explained by influence of scalar gravitational potential on the clock. In the second effect, difference of received radiation wavelength from the standard value arises in the case, when the radiation source and the radiation receiver are placed in regions with different gravitational potentials. In both general relativity and covariant theory of gravitation, these effects are caused by influence of field on its proper time at observation point and are calculated with the help of metric tensor.

In case when gravitational field strength and gravitational torsion field in covariant theory of gravitation (gravitomagnetic field in general theory of relativity) are equal to zero, the phase shift due to action of gravitational field potentials can be considered as gravitational analogue of Ehrenberg–Siday–Aharonov–Bohm effect.

The idea that the action function has physical meaning of the function, describing change of such intrinsic properties of bodies and reference frames, as the rate of proper time flow and the rate of rise of phase angle of periodic processes, appeared in works of Sergey Fedosin in 2012. [2]

Contents

Theoretical description

Covariant theory of gravitation

For comparison, the formulas for calculation of gravitational phase shift presented below are supplemented by similar formulas for phase shift due to electromagnetic field.

Influence of four-potentials of fields

For gravitational and electromagnetic fields, the difference in clock readings in weak field approximation is described by the formulas: [2]

~\tau _{1}-\tau _{2}={\frac {m}{mc^{2}}}\int _{{1}}^{{2}}D_{\mu }\,dx^{\mu },\qquad \tau _{1}-\tau _{2}={\frac {q}{mc^{2}}}\int _{{1}}^{{2}}A_{\mu }\,dx^{\mu }.\qquad (1)

 

Here is gravitational 4-potential  ~D_{\mu }=\left({\frac {\psi }{c}},-{\mathbf {D}}\right),  where  ~\psi  is scalar potential and ~{\mathbf {D}}  is vector potential of gravitational field; the electromagnetic 4-potential  ~A_{\mu }=\left({\frac {\varphi }{c}},-{\mathbf {A}}\right),  where ~\varphi   is scalar potential and ~{\mathbf {A}}  is vector potential of electromagnetic field; ~dx^{\mu }  means 4-displacement, ~c  is speed of light, ~m  and  ~q  are mass and charge of the clock.

The clock 2, which is out of the field and measures the time ~\tau _{2} , is check one and the clock 1 measures the time ~\tau _{1}  and is under influence of 4-field potentials ~D_{\mu }  or  ~A_{\mu }. Time points 1 and 2 within the integrals indicate the beginning and the end of field action.

From time difference in  we can move to phase shift for the same type of processes in field and outside it, or occurring in different states of motion. To do this, in the denominators it is necessary to replace ~mc^{2}  by the value of characteristic angular momentum. For the level of atoms it is the Dirac constant ~\hbar :

~\theta _{1}-\theta _{2}={\frac {m}{\hbar }}\int _{{1}}^{{2}}D_{\mu }\,dx^{\mu },\qquad \theta _{1}-\theta _{2}={\frac {q}{\hbar }}\int _{{1}}^{{2}}A_{\mu }\,dx^{\mu }.\qquad (2)

 

The phase shift, obtained due to electromagnetic 4-potential ~A_{\mu }, acting on a particle with the charge ~q, is proved by the Aharonov-Bohm effect in quantum physics. The phase shift in gravitational 4-potential is also confirmed in the papers, [3] [4]  where it was found that the phase shift is proportional to integral of gravitational vector potential ~{\mathbf {D}} :

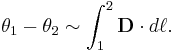
~\theta _{1}-\theta _{2}\sim \int _{{1}}^{{2}}{\mathbf {D}}\cdot d{\mathbf {\ell }}.

 

From the integral equations given above, we can go to differential equations. It is convenient to denote as ~t  the coordinate reference clock time of external observer located beyond the field of the system. If ~d{\mathbf {r}}  is a displacement of the clock 1 in the field and ~{\mathbf {v}}  is speed of the clock, for gravitational and electromagnetic fields respectively we can write:

~D_{\mu }\,dx^{\mu }=\psi dt-{\mathbf {D}}\cdot d{\mathbf {r}}=(\psi -{\mathbf {D}}\cdot {\mathbf {v}})dt.

 

~A_{\mu }\,dx^{\mu }=\varphi dt-{\mathbf {A}}\cdot d{\mathbf {r}}=(\varphi -{\mathbf {A}}\cdot {\mathbf {v}})dt.

 

Substituting this into ~(1) and into ~(2) and differentiating with respect to time, we obtain respectively:

 

~{\frac {d\tau _{1}}{dt}}={\frac {d\tau _{2}}{dt}}+{\frac {1}{c^{2}}}(\psi -{\mathbf {D}}\cdot {\mathbf {v}}),\qquad {\frac {d\tau _{1}}{dt}}={\frac {d\tau _{2}}{dt}}+{\frac {q}{mc^{2}}}(\varphi -{\mathbf {A}}\cdot {\mathbf {v}}).\qquad (3)

 

~\omega _{1}=\omega _{2}+{\frac {m}{\hbar }}(\psi -{\mathbf {D}}\cdot {\mathbf {v}}),\qquad \omega _{1}=\omega _{2}+{\frac {q}{\hbar }}(\varphi -{\mathbf {A}}\cdot {\mathbf {v}}).\qquad (4)

 

Here ~{\frac {d\tau _{1}}{dt}} is the rate of time change of clock 1 due to scalar field potential and motion in vector potential of corresponding field, ~{\frac {d\tau _{2}}{dt}} is the rate of time change of clock 2 with the same motion without field, ~\omega _{1}={\frac {d\theta _{1}}{dt}} is angular frequency of some process occurring in the field, ~\omega _{2}={\frac {d\theta _{2}}{dt}} is angular frequency of a similar process associated with the control object 2 located outside field.

In static experiments in gravitational or electric field, it is convenient to consider difference between the rate of time of clocks or the frequency difference of periodic processes in two neighboring points in space where all the clocks and objects are stationary and their velocities are zero. Let us write the equalities ~(3) and ~(4) for clock 1 at the speed of the clock ~{\mathbf {v}}=0, as well as for a stationary clock 3 located in the field at point 3 not far from clock 1:

~{\frac {d\tau _{1}}{dt}}={\frac {d\tau _{2}}{dt}}+{\frac {\psi _{1}}{c^{2}}},\qquad {\frac {d\tau _{1}}{dt}}={\frac {d\tau _{2}}{dt}}+{\frac {q\varphi _{1}}{mc^{2}}}.

~{\frac {d\tau _{3}}{dt}}={\frac {d\tau _{2}}{dt}}+{\frac {\psi _{3}}{c^{2}}},\qquad {\frac {d\tau _{3}}{dt}}={\frac {d\tau _{2}}{dt}}+{\frac {q\varphi _{3}}{mc^{2}}}.

~\omega _{1}=\omega _{2}+{\frac {m\psi _{1}}{\hbar }},\qquad \omega _{1}=\omega _{2}+{\frac {q\varphi _{1}}{\hbar }}.

~\omega _{3}=\omega _{2}+{\frac {m\psi _{3}}{\hbar }},\qquad \omega _{3}=\omega _{2}+{\frac {q\varphi _{3}}{\hbar }}.

Вычитая соответствующие равенства друг из друга, имеем:

~{\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}={\frac {\psi _{1}-\psi _{3}}{c^{2}}},\qquad {\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}={\frac {q(\varphi _{1}-\varphi _{3})}{mc^{2}}}.\qquad (5)

~\omega _{1}-\omega _{3}={\frac {m(\psi _{1}-\psi _{3})}{\hbar }},\qquad \omega _{1}-\omega _{3}={\frac {q(\varphi _{1}-\varphi _{3})}{\hbar }}.\qquad (6)

In ~(5) it is seen that the rates of clocks at points with different scalar potentials of field do not match. In case of gravitational field it gives gravitational time dilation, which results in gravitational redshift. The similar effects are also expected, if gravitational field is replaced by electromagnetic field. These effects in electromagnetic field have not been measured yet because of their smallness.

The gravitational phase shift ~(6) was measured using an interferometer on two beams of rubidium atoms, with one beam located near a mass that creates an additional gravitational potential. [5]

The gravitational potential on the Earth’s surface is defined by the formula:

~\psi _{1}=-{\frac {GM_{e}}{R_{e}}},

where ~M_{e} and ~R_{e} are the mass and radius of the Earth, ~G is gravitational constant.

At the point, which is located at the distance ~d=1 meter above the Earth's surface, potential will be equal to:

~\psi _{3}=-{\frac {GM_{e}}{R_{e}+d}}.

Therefore, for difference in the clock rate at points 1 and 3, which differ in height by 1 meter, we can write:

~{\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}\approx -{\frac {GM_{e}d}{R_{e}^{2}c^{2}}}={\frac {\Gamma _{e}d}{c^{2}}}=-1.1\cdot 10^{{-16}}.

Here ~\Gamma _{e}=-{\frac {GM_{e}}{R_{e}^{2}}} is gravitational field strength, which is equal in absolute value to free fall acceleration 9.8 m/s2.

As we can see, if a period of time ~dt=1 second passes, the lower clock will lag behind the upper clock by about 10-16 seconds.

Angular frequencies in ~(6) are meaningful local reduced Compton angular frequencies in a given points of field and related to the rates of fixed clock in ~(5), and it can be written as:

~\omega _{1}=\omega _{C}{\frac {d\tau _{1}}{dt}},\qquad \omega _{3}=\omega _{C}{\frac {d\tau _{3}}{dt}},

here ~\omega _{C}={\frac {mc^{2}}{\hbar }} is reduced Compton angular frequency in absence of gravitational or electromagnetic field.

The work in gravitational field of moving masses between points with different scalar potentials is ~W_{g}=m(\psi _{1}-\psi _{3}), and the work on charge transfer in an electric field is equal to ~W_{e}=q(\varphi _{1}-\varphi _{3}). In carrying out this work there is a change of location of mass or charge in the field, as well as change in the local reduced Compton angular frequency. Taking into account ~(6) it turns out that the work is equal to product of Planck constant to the change of reduced Compton angular frequency: [6]

~W=\hbar (\omega _{1}-\omega _{3}).

Influence of field tensors

The energy of fields associated with matter unit with mass ~m  depends not only on absolute value of four-potentials, but also on their rates of change in spacetime, that is on the field strengths. Each additional energy must influence the inner properties of matter, including the proper time flow rate. The field strengths are included in action function through the field tensors, so that for corresponding time shifts in gravitational and electromagnetic fields we can expect the following:

~\tau _{1}-\tau _{2}=-{\frac {1}{16\pi Gm}}\int _{{1}}^{{2}}\left(\int \Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}\right)dt.\qquad (7)

 

~\tau _{1}-\tau _{2}={\frac {1}{4\mu _{0}mc^{2}}}\int _{{1}}^{{2}}\left(\int F_{{\mu \nu }}F^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}\right)dt.

 

Here  ~\mu _{0}  is vacuum permeability, ~\Phi _{{\mu \nu }}  is gravitational tensor; ~F_{{\mu \nu }}  is electromagnetic tensor; ~g  is determinant of metric tensor.

From these formulas it follows that gravitational field strength inside volume of the clock must accelerate their rate and the electromagnetic field strength must on the contrary slow down the clock rate, as opposed to the case, when there is no field.

To estimate the effect in gravitational field we use weak field approximation, in which we can assume that  ~g=-1,   ~\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}=-{\frac {2}{c^{2}}}(\Gamma ^{2}-c^{2}\Omega ^{2}), and the volume element  ~dV=dx^{1}dx^{2}dx^{3}. For two clocks, located at adjacent points 1 and 3, in the absence of gravitational torsion field ~\Omega , which usually makes small contribution, taking into account ~(7) we can write the following:

~{\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}\approx {\frac {1}{8\pi Gmc^{2}}}\int (\Gamma _{1}^{2}-\Gamma _{3}^{2})dV.\qquad (8)

 

Suppose points 1 and 3 are located near the Earth’s surface and are separated in height by the distance ~d=1  meter. We choose the mass ~m  and the volume  ~V of the clock in such a way, that the relation  ~m=\rho _{e}V  would hold, where ~\rho _{e}  is average density of the Earth. Under these conditions, we find:

 

~{\frac {d\tau _{1}}{dt}}-{\frac {d\tau _{3}}{dt}}\approx {\frac {\Gamma _{e}^{2}d}{2\pi GR_{e}\rho _{e}c^{2}}}=7.3\cdot 10^{{-17}},

 

which is comparable in magnitude to the effect of gravitational time dilation from the action of gravitational scalar potential, but has the opposite sign. To test the effect of gravitational or electric field strength on the slowing down of clock time according to the formulas given above, more precise experiments are needed.

Let there be two gravitationally interacting bodies, distant from other bodies. On the line connecting these two bodies, one can find a small region of space where total gravitational field strength ~\Gamma  everywhere vanishes, and total scalar potential becomes equal to the sum of potentials of these bodies. In this region, difference in the rates of time at two neighboring points 1 and 3 depends on the total scalar potential at these points according to ~(5) and does not depend on the total field strength of the bodies according to ~(8). The same will be true for the difference in local reduced Compton angular frequencies at two neighboring points.

References

  1. A. Einstein, "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen", Jahrbuch der Radioaktivität und Elektronik 4, 411–462 (1907); English translation, in "On the relativity principle and the conclusions drawn from it", in "The Collected Papers", v.2, 433-484 (1989); also in H M Schwartz, "Einstein's comprehensive 1907 essay on relativity, part I", American Journal of Physics vol.45,no.6 (1977) pp.512-517; Part II in American Journal of Physics vol.45 no.9 (1977), pp.811–817; Part III in American Journal of Physics vol.45 no.10 (1977), pp.899-902, see parts I, II and III.
  2.  2,0 2,1 Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55-75. http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023.
  3. B. S. DeWitt, Superconductors and gravitational drag. Phys. Rev. Lett., Vol. 24, 1092–3 (1966).
  4. G. Papini, Particle wave functions in weak gravitational fields. Nuovo Cimento B, Vol.v52, 136–41 (1967).
  5. Overstreet, Chris; Asenbaum, Peter; Curti, Joseph; Kim, Minjeong; Kasevich, Mark A. Observation of a gravitational Aharonov-Bohm effect, Science, Vol. 375, No 6577, pp. 226-229 (2022). https://doi.org/10.1126%2Fscience.abl7152.
  6. John A. Macken. The Universe is Only Spacetime. Chapter 8. Analysis of Gravitational Attraction. Gravitational Energy Storage. p. 8-25 (2015).

 

See also

External links

 

Source: http://sergf.ru/gpsen.htm

On the list of pages