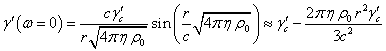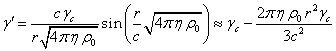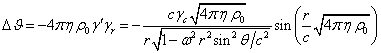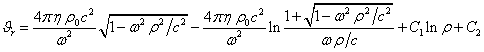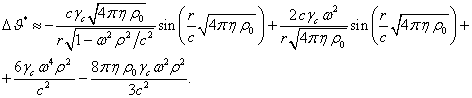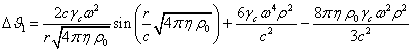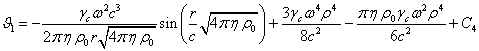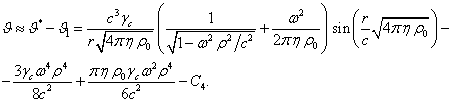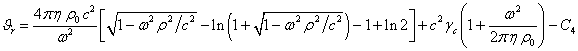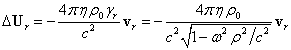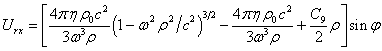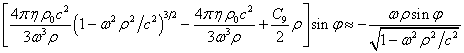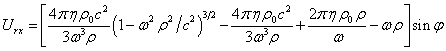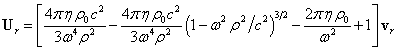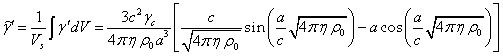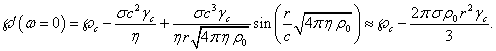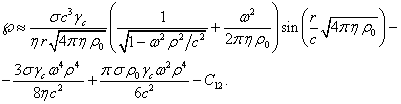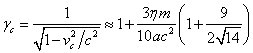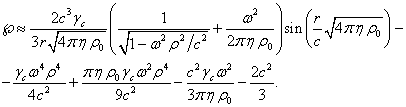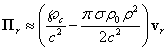In English

Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://rdcu.be/ccV9o.

https://doi.org/10.1007/s00161-020-00960-7

Потенциалы поля ускорений и поля давления во вращающейся релятивистской однородной системе

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail: fedosin@hotmail.com

Скалярные и векторные потенциалы поля ускорений и поля давления впервые вычисляются для вращающейся релятивистской однородной системы, и находится зависимость потенциалов от угловой скорости. Эти потенциалы сравниваются с потенциалами для не вращающейся однородной системы, найденными ранее. Вращение приводит к появлению векторных потенциалов, которые в каждой точке оказываются направленными вдоль соответствующей линейной скорости вращения. Расчёт показывает, что для вращающихся звёздных объектов вклад в векторные потенциалы полей от собственного хаотического движения частиц мал по сравнению с вкладом от вращения, и потому может не учитываться. Из выражения для потенциала поля давления следует релятивистская формула, связывающая давление, плотность массы и среднеквадратичную скорость частиц. Данная формула в пределе малых скоростей соответствует выражению для давления в молекулярно-кинетической теории. При вычислении потенциалов применяется новый, ранее не используемый метод, учитывающий потенциалы двух различных тел, цилиндра и сферы, при решении волнового уравнения для вращающейся системы.

Ключевые слова: поле ускорений; поле давления; скалярный потенциал; векторный потенциал; вращение; однородная система.

The potentials of the acceleration field and pressure field in rotating relativistic uniform system

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

E-mail: fedosin@hotmail.com

The scalar and vector potentials of the acceleration field and the pressure field are calculated for the first time for a rotating relativistic uniform system, and the dependence of the potentials on the angular velocity is found. These potentials are compared with the potentials for the non-rotating uniform system that have been found previously. The rotation leads to the appearance of vector potentials, which at each point turn out to be directed along the corresponding linear velocity of rotation. The calculation shows that for rotating stellar objects the contribution to the fields’ vector potentials from the proper random motion of particles is small compared to the contribution from rotation and may not be taken into account. From the expression for the pressure field potential a relativistic formula follows that relates the pressure, mass density, and mean square velocity of the particles. This formula in the limit of low speeds corresponds to the expression for the pressure in molecular kinetic theory. When calculating the potentials, a new method is used that takes into account the potentials of two different bodies, a cylinder and a sphere, for solving the wave equation of rotating system.

Keywords: acceleration field; pressure field; scalar potential; vector potential; rotation; uniform system.

1. Введение

Вывод формул для поля давления в движущемся веществе не является тривиальной задачей и в общем случае требует решения дифференциальных уравнений. Одним из методов является решение уравнения Навье-Стокса при заданном поле скоростей и известных граничных условиях [1]. Выражение для давления в [2] было получено путём обобщения уравнения Бернулли, в [3-4] поле давления находилось численно с помощью уравнений, содержащих давление и поле скоростей, При этом поле давления в веществе рассматривается упрощённо, как некоторое скалярное поле, зависящее от времени и координат. В [5] поле давления с учётом электромагнитных явлений рассматривается в рамках гидродинамики и термодинамики, используя подходы Эйлера и Лагранжа при описании движения вещества. Известны также работы по определению потенциалов электромагнитного поля во вращающихся телах [6-11].

Целью данной статьи является исследование вращающейся релятивистской однородной системы с помощью методов аналитической механики в приближении непрерывно распределённого вещества.

Релятивистская однородная система является одной из моделей современной физики и находит своё применение в самых разных областях [12-16]. Данная модель описывает различные гравитационно связанные системы на основе теории поля и потому оказывается намного более точной по сравнению с моделью однородной системы классической механики. Релятивистская модель обобщает классическую однородную модель и вместо трёхмерных векторов использует четырёхмерный формализм. В отличие от феноменологического термодинамического подхода, поле давления трактуется не как скалярное, а как векторное поле, обладающее собственным 4-потенциалом, тензором давления и тензором энергии-импульса.

Уравнения поля позволяют с помощью принципа наименьшего действия вывести соотношения, возникающие между действующими в веществе силами. Чем меньше внутри системы градиенты плотности вещества, тем ближе по своим свойствам эта система становится к релятивистской однородной системе. Как следствие, полученные теоретические результаты могут быть применены, например, к динамике космических газовых облаков и к Метагалактике в целом. Интересным может быть изучение движения намагниченного вещества в ядре Земли в связи с проблемой происхождения магнитного поля и смены магнитных полюсов.

В [17-21] были вычислены потенциалы и напряжённости различных векторных полей в покоящейся однородной системе. В такой системе глобальные векторные потенциалы полей равны нулю. Следующим шагом является вычисление потенциалов для вращающейся релятивистской однородной системы. Необходимость такого шага следует из того, что только учёт векторных потенциалов, появляющихся при вращении, позволяет корректно вычислить такие физические величины, как момент импульса и релятивистская энергия системы. Хорошо известно, что в присутствии гравитационных и электромагнитных полей, вместо обычного импульса и момента импульса, используются обобщённые импульсы, выражаемые через векторные потенциалы полей. Указанные величины могут быть использованы для оценки соответствующих величин у наблюдаемых тел типа нуклонов и нейтронных звёзд, поскольку эти объекты достаточно близки по своим свойствам к вращающейся релятивистской однородной системе.

Если говорить о потенциалах поля ускорений и поля давления, то с помощью этих потенциалов становится возможным вычислить зависимость плотности массы от координат, распределение скоростей типичных частиц, давления и температуры в рассматриваемой системе. Ранее подобные расчёты были сделаны без учёта вращения релятивистской однородной системы и применены для оценки параметров звёзд и планет [13], для вычисления кинетической энергии системы [14], определения зависимости среднеквадратичной скорости от координат [16].

Далее мы будем считать, что физическая система имеет сферическую форму и настолько плотно заполнена частицами, что можно использовать приближение сплошной среды и вычислять различные величины с помощью интегралов по объёму системы. В качестве основных полей обычно рассматриваются гравитационное и электромагнитное поля, поле ускорений и поле давления, создаваемые частицами, и эти поля поддерживают как целостность системы, так и состояние её постоянного вращения.

В данной статье, с целью уменьшения её объёма, мы сосредоточимся лишь на отыскании потенциалов поля ускорений и поля давления. Выделенность этих полей имеет ещё одну причину – они действуют как правило локально, в том смысле, что обращаются в нуль за пределами вещества. Локальность действия поля ускорений и поля давления позволяет заметно упростить решение уравнений для потенциалов этих полей.

В противоположность этому, гравитационное и электромагнитное поля существуют и за пределами вещества. По всей видимости, это связано с фундаментальным различием указанных полей. Имеется теоретический подход, согласно которому гравитоны и заряженные частицы электрогравитационного вакуума действуют внутри и за пределами тел, приводя к соответствующим силам в веществе данных тел [22-23]. Для описания такого действия вводятся понятия гравитационного и электромагнитного полей. Поле давления учитывает те силы, которые появляются при механических столкновениях частиц друг с другом. Для описания силы торможения движения соседних направленных и взаимодействующих потоков частиц вводится поле диссипации [12].

Если все эти поля рассматривать как векторные, то и поле ускорений, задающее ускорение частиц, также следует полагать векторным полем. Действительно, в уравнении движения частиц ускорение связывается с действующими силами, которые определяются через тензоры полей [24]. Кроме этого, учёт поля ускорения позволяет получить в ковариантном виде не только ускорение, но и энергию, включая энергию покоя системы [15]. Это становится возможным благодаря тому, что поле ускорений как самостоятельное поле вводится в функцию Лагранжа. Последующее применение принципа наименьшего действия позволяет вывести уравнения поля ускорения и получить уравнение движения [19]. В простейшем случае поле ускорений задаёт силу инерции в виде произведения массы на ускорение, тогда как другие поля задают действующие на данную массу силы. Тогда связь между силой инерции и суммой сил от других полей выражается известным вторым законом Ньютона. В частности, с помощью поля ускорения точно воспроизводится уравнение Навье-Стокса [12].

2. Поле ускорений

Уравнения для поля ускорений по форме напоминают уравнения Максвелла и представлены в [19]. В рамках специальной теории относительности они выглядят так:

, , , , (1)

где есть коэффициент поля ускорений, – фактор Лоренца для движущихся внутри сферы частиц, – скорость частиц в системе отсчёта , связанной с центром сферы, – плотность массы произвольной частицы в сопутствующей ей системе отсчёта, – скорость света, и – соответственно напряжённость и соленоидальный вектор поля ускорений.

4-потенциал задаётся через скалярный потенциал и векторный потенциал поля ускорений таким образом, что выполняются соотношения:

, . (2)

Подстановка (2) в (1) приводит к волновым уравнениям для потенциалов:

, .

Согласно (1-2), поле ускорений описывается двумя потенциалами и , и двумя векторами и . Вектор по своим свойствам подобен магнитному полю, возникающему вследствие движения заряженных частиц и за счёт запаздывания распространения электромагнитного воздействия. Известно, что у неподвижной частицы равны нулю как её векторный потенциал, так и её магнитное поле. Это же справедливо и для соленоидального вектора , отражающего релятивистский характер поля ускорений.

Если рассматривать средние величины, то в стационарной системе скорость движения частиц, вектор плотности массового тока , а также потенциалы и не зависят от времени, но являются функциями пространственных координат. В результате в волновых уравнениях остаются только лапласианы:

, . (3)

С целью упрощения будем считать, что вещество внутри сферы вращается с одной и той же постоянной угловой скоростью относительно оси, проходящей через центр сферы. С помощью правила релятивистского сложения скоростей для абсолютной скорости и фактора Лоренца произвольной частицы в системе отсчёта можно записать:

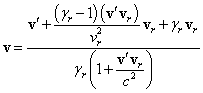, , (4)

где есть скорость хаотического движения частицы в системе отсчёта , вращающейся вместе с веществом с угловой скоростью ; – линейная скорость движения системы отсчёта в месте расположения частицы, возникающая за счёт вращения в системе отсчёта ; – фактор Лоренца для скорости , – фактор Лоренца для скорости .

Усредним выражения (4) по объёму в небольшой окрестности вокруг рассматриваемой точки так, чтобы в этом объёме присутствовало достаточное количество частиц. Скорость хаотического движения представлена в (4) таким образом, что после усреднения вклады от членов, содержащих , обнуляются. Это происходит потому, что у разных частиц скорость имеет различную направленность, в том числе противоположную. Тогда из (4) для средних величин следует: , .

Для сферической системы с частицами в отсутствие общего вращения вещества фактор Лоренца зависит от текущего радиуса и от величины фактора Лоренца в центре сферы [17]:

.

Данное выражение было получено в том предположении, что частицы вещества не имеют собственного вращения, движутся инерциально и хаотично.

Будем считать далее, что в системе отсчёта , вращающейся вместе с веществом с угловой скоростью , фактор Лоренца определяется аналогичной формулой

. (5)

с тем исключением, что в центре вращающейся сферы используется фактор Лоренца , который может отличаться по величине от для покоящейся сферы.

Это означает, что если в системе отсчёта имеется вращающаяся релятивистская однородная система, то при переходе в сопутствующую вращающуюся систему отсчёта справедливо (5) и общее вращение не изменяет зависимость фактора Лоренца от текущего радиуса.

По своему смыслу такая ситуация соответствует принципу относительности, когда в инерциальной системе отсчёта одновременное увеличение скорости всех частиц системы на одну и ту же величину не изменяет состояния системы. Отличие лишь в том, что вращение изменяет скорости частиц по-разному в зависимости от текущего радиуса, что делает систему отсчёта неинерциальной. Поэтому предположение о применении (5) для вращающейся системы отсчёта можно рассматривать как первое приближение к действительности.

В сферических координатах амплитуда линейной скорости вращения выражается формулой: , где угол отсчитывается от оси , а частицы вещества вращаются в плоскостях, параллельных плоскости . В цилиндрических координатах скорость определяется выражением .

Соответственно, фактор Лоренца можно записать так:

, (6)

где есть расстояние от оси вращения до рассматриваемой точки.

Вместо реальных частиц вещества удобно полагать, что вещество состоит из типичных частиц, характеризующих в среднем все свойства системы. После усреднения всех величин по объёму получается, что уравнения для типичных частиц связывают между собой усреднённые физические величины. Подстановка в (3) вместо и вместо , с учётом (5) и (6) даёт:

. (7)

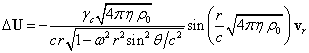. (8)

В сферических координатах для произвольной функции лапласиан этой функции для случая имеет вид:

. (9)

Для покоящейся сферы при уравнение (3) для скалярного потенциала и решение этого уравнения имеют вид:

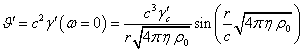, . (10)

Потенциал в (10) зависит только от радиуса . Подстановка вместо в (9) позволяет вычислить лапласиан и сравнить результат с первым выражением в (10).

Решим вспомогательную задачу и найдём скалярный потенциал поля ускорений для случая чисто вращательного движения однородной системы в виде бесконечного длинного цилиндра без учёта собственного движения частиц. Из (3) и (6) следует:

. (11)

Лапласиан произвольной функции в цилиндрических координатах представляется так:

. (12)

После замены на в (12) с учётом (11) приходим к уравнению:

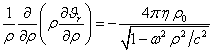. (13)

В (13) потенциал не зависит от угла вследствие симметрии относительно оси вращения. Предполагается также, что не зависит и от координаты внутри цилиндра. Это соответствует тому, что является некоторой функцией от фактора Лоренца (6) частиц вращающегося вещества, который зависит лишь координаты и угловой скорости вращения . Заметим, что при движении свободной частицы или частиц вещества релятивистской однородной системы потенциал поля ускорения просто пропорционален соответствующему фактору Лоренца. То, что зависит только от , является простейшим выбором для зависимости потенциала вращающегося цилиндра. Мы будем рассматривать как вспомогательный потенциал для определения полного потенциала вращающейся сферической однородной релятивистской системы.

Решением уравнения (13) является следующеe:

.

Постоянные и следует выбрать таким образом, чтобы не зависело ни от , ни от , которые обращаются в бесконечность при . Это даёт:

. (14)

Вопрос о выборе постоянной будет решён в (20), после решения уравнения (7) для вращающейся сферической однородной релятивистской системы.

В случае прямолинейного движения твёрдой материальной точки без собственного вращения её скалярный потенциал равен , где есть фактор Лоренца частицы. Что касается векторного потенциала поля ускорения для такой твёрдой точки, то он равен , где есть скорость частицы [25].

В связи с этим умножим на и будем рассматривать величину как первое приближение к искомой величине скалярного потенциала . Учитывая, что и , выразим в (5) и в (6) через координаты , и вычислим лапласиан в декартовых координатах:

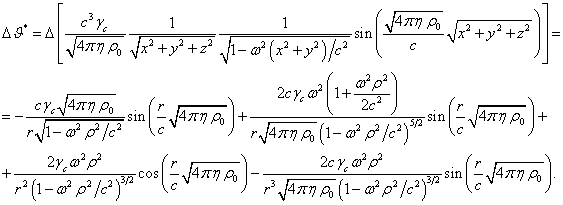
(15)

Результат вычисления в правой части (15) выражен через радиус и цилиндрическую координату . Используя разложение функций вида , , разложим косинус и синус в двух последних членах в правой части (15). При этом основные члены разложения сократятся и в итоге останется член, содержащий в знаменателе квадрат скорости света :

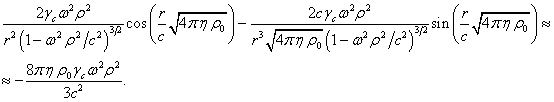
Преобразуем второй член в правой части (15), считая что :

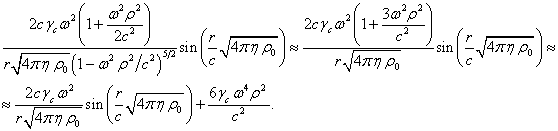
Тогда в первом приближении можно записать:

(16)

Найдём теперь такую функцию , чтобы её лапласиан равнялся сумме последних трёх членов в правой части (16):

.

Учитывая вид лапласиана (9) в сферических координатах, и соответственно вид лапласиана (12) в цилиндрических координатах, находим решение, не содержащее бесконечностей при и при :

. (17)

Вычитая почленно равенство для из равенства (16), имеем:

.

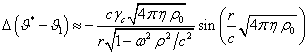Из сравнения данного равенства с (7) с учётом , равенств (5), (6), (17) получаем приблизительное выражение для скалярного потенциала поля ускорений:

(18)

Будем рассматривать внутреннюю область внутри сферы при малых и , то есть область вблизи оси вращения и вблизи центра сферы. В этом случае синус в (18) можно заменить на его аргумент:

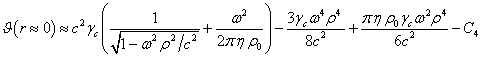. (19)

Пользуясь свободой калибровки скалярного потенциала, приравняем потенциал вращающегося цилиндра вблизи оси цилиндра и потенциал вблизи центра вращающейся сферы. С этой целью устремим цилиндрическую координату в равенствах (14) и в (19) к нулю и приравняем данные равенства. Это позволяет оценить постоянную и уточнить вид скалярного потенциала в (14):

.

.

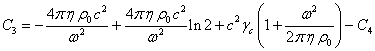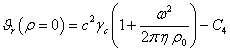Отсюда следует, что на оси вращения, где , потенциал равен . Если положить постоянную , то потенциал на оси вращения цилиндра не будет зависеть от угловой скорости вращения . В этом случае находим:

. (20)

При малых потенциал в (20) перестаёт зависеть от и становится приблизительно равным величине , причём есть фактор Лоренца в центре сферы и в центре соответствующего цилиндра. Чтобы проверить эту формулу, достаточно решить уравнение (13) при для случая неподвижного цилиндра. В этом случае решение имеет вид:

.

В данном решении необходимо положить во избежание бесконечности при , и учесть, что при потенциал должен равняться . Следовательно, должно быть , и мы приходим к тому, что .

Выражение (20) имеет интересную аналогию с зависимостью химического потенциала вращающегося твёрдого тела в состоянии теплового равновесия [26], имеющую в наших обозначениях следующий вид:

,

где есть химический потенциал в отсутствие вращения, зависящий от давления и температуры ; – масса молекулы; в общем случае есть потенциальная энергия молекулы в некотором поле, которая для случая поля вращения была приравнена к величине кинетической энергии молекулы , взятой с отрицательным знаком.

По мере роста координаты и удалении от оси вращения химический потенциал уменьшается, и это же следует для зависимости потенциала в (20. При этом потенциал можно считать аналогом для , а первый член в правой части (20) аналогом для .

Подстановка в (18) даёт:

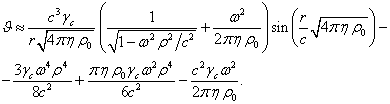(21)

Если в (21) угловая скорость вращения обращается в нуль, потенциал становится равным потенциалу в (10).

3. Векторный потенциал поля ускорений

В покоящейся в целом релятивистской однородной системе векторные потенциалы полей, включая и поле ускорений, равны нулю благодаря хаотическому движению частиц. Так получается благодаря принципу суперпозиции, когда векторные потенциалы отдельных частиц суммируются векторным способом.

Для случая вращения цилиндра без учёта собственного движения частиц вещества из (3) и (6) в цилиндрических координатах следует уравнение для векторного потенциала :

. (22)

Из связи между декартовыми и цилиндрическими координатами в виде , , вытекает, что в отсутствие движения частиц вещества в направлении оси компоненты линейной скорости определяются так:

. (23)

В (23) присутствует угловая скорость вращения .

Спроектируем уравнение (22) на ось с учётом (23) и выражения (12) для лапласиана в цилиндрических координатах:

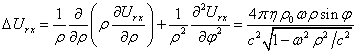. (24)

Подставим в (24) выражение , где функция зависит только от . Это позволяет избавиться от :

.

.

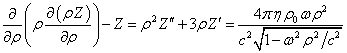Здесь , . Дифференциальное уравнение для вычисления можно преобразовать путём умножения на и затем проинтегрировать правую часть:

.

.

Величину можно также проинтегрировать по частям:

.

Сравнивая интегралы для в двух последних выражениях, находим:

.

Данное уравнение имеет следующее общее решение:

.

Теперь можно найти первую компоненту векторного потенциала:

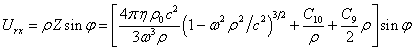. (25)

В (25) необходимо ещё уточнить значения постоянных коэффициентов и . По аналогии с калибровкой скалярного потенциала в (14), положим, что если стремится к нулю, то потенциал не должен обращаться в бесконечность. Для этого достаточно выбрать значение постоянной . Это даёт:

. (26)

При малых угловых скоростях векторный потенциал должен быть пропорционален линейной скорости и фактору Лоренца , как это имеет место для движения твёрдой точки: . Для компоненты при условии , с учётом (23), (26) и выражения в цилиндрических координатах согласно (6) это можно записать так:

.

Отсюда следует, что , и для проекции векторного потенциала на ось получается следующее:

. (27)

Повторяя все шаги, начиная с (24), и проектируя уравнение (22) на оси и , находим соответственно остальные компоненты векторного потенциала:

, .

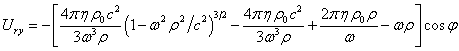(28)

Из сравнения (23), (27), (28) следует, что для векторного потенциала справедлива формула:

. (29)

Согласно (29), векторный потенциал направлен вдоль линейной скорости вращения вещества цилиндра. Вблизи оси вращения, где , а также при малых значениях угловой скорости потенциал стремится по своей величине к скорости вращения .

Чтобы учесть вклад в векторном потенциале от собственного движения частиц в рамках сферической релятивистской однородной системы, сравним уравнение (8) для потенциала , и уравнение (22) для потенциала . Правая часть (8) оказывается больше, чем правая часть (22), в раз, где есть фактор Лоренца (5). В первом приближении следует считать, что и потенциал окажется в больше, чем потенциал . Поскольку является функцией от текущего радиуса , определим среднюю величину как среднее по объёму сферы , используя в данном случае элемент объёма :

. (30)

В большинстве случаев , и тогда 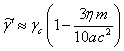, где есть произведение плотности массы на объём сферы , обозначает фактор Лоренца частиц в центре сферы, есть радиус сферы. Умножая в (29) на (30), получаем оценку векторного потенциала поля ускорений для вращающейся релятивистской однородной системы:

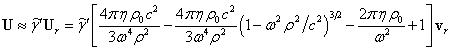. (31)

Для примера рассмотрим нейтронную звезду как релятивистскую однородную систему [21]. У такой звезды с массой 1,35 масс Солнца при радиусе км средняя плотность массы кг/м³ , а фактор Лоренца в центре может достигать величины . Для звезды нужно учесть соотношение , где есть гравитационная постоянная, и угол радиан. С этими данными усреднённый фактор Лоренца для собственного движения частиц в (30) получается равным , что меньше, чем , как и следовало ожидать для средней по объёму величины. Данный расчёт показывает, что вклад в векторный потенциал (31) для звёзд невелик.

4. Поле давления

Уравнения для напряжённостей и потенциалов векторного поля давления в рамках специальной теории относительности имеют следующий вид [17], [19]:

, , , . (32)

, . (33)

, , . (34)

Здесь и – соответственно напряжённость и соленоидальный вектор поля давления, – коэффициент поля давления, – 4-потенциал поля давления, и – скалярный и векторный потенциалы, . Волновые уравнения (33) для потенциалов получаются из уравнений (32) с учётом (34).

Если система частиц имеет сферическую форму и вращается с постоянной угловой скоростью , потенциалы не будут зависеть от времени. Из (33) тогда следует:

, . (35)

Мы считаем, что в системе отсчёта , вращающейся вместе с веществом с угловой скоростью , фактор Лоренца имеет тот же вид, что и в (5), соответствуя системе частиц, движущихся только хаотично в не вращающейся в целом системе. Подставляя вместо в (35), находим скалярный потенциал поля давления для не вращающейся в целом системы [17]:

.

(36)

Если не брать в учёт собственное движение частиц со скоростью и фактором Лоренца , а учитывать только движение частиц за счёт вращения, в (35) вместо следует подставить фактор Лоренца (6). Это даёт уравнение для скалярного потенциала вращающегося цилиндра в цилиндрических координатах, подобное (11):

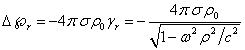. (37)

Следовательно, решение уравнения (37) будет аналогично (14):

. (38)

Для сравнения, в [25] для случая прямолинейного движения с постоянной скоростью твёрдой частицы без собственного вращения 4-потенциал поля давления был определён так:

, (39)

где и обозначают инвариантное давление и плотность массы в системе отсчёта частицы, безразмерное отношение пропорционально энергии давления частицы в расчёте на единицу массы частицы, есть 4-скорость частицы с ковариантным индексом. При этом скалярный потенциал в (39) получается равным , а векторный потенциал будет .

Прежде чем определять постоянную в (38), найдём решение уравнения (35) для вращающейся сферической системы с учётом собственного хаотического движения частиц. Это означает, что в (35) вместо необходимо использовать выражение :

. (40)

Приблизительное решение уравнения (40) подобно решению уравнения (7) и может быть записано аналогично (18):

(41)

В (41) присутствует постоянная , так как потенциал в (40) определяется с точностью до константы. При малых можно положить, что в (41). Это даёт следующее:

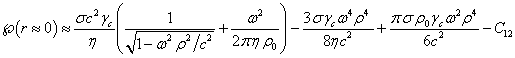. (42)

Мы можем приравнять выражения (38) и (42) друг к другу, если в этих выражениях устремить цилиндрическую координату к нулю. Тем самым мы осуществим один из возможных вариантов калибровки потенциала вращающегося цилиндра. Это позволяет выразить и уточнить вид (38):

.

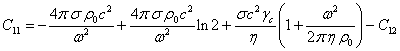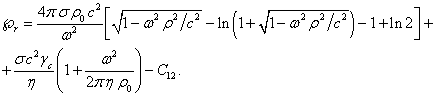(43)

На оси вращения при в (43) будет: 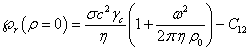. Выберем таким образом, чтобы на оси вращения не зависело от угловой скорости вращения . Это возможно, если , причём не зависит от . При этом будет .

Подставим в (41) и (43):

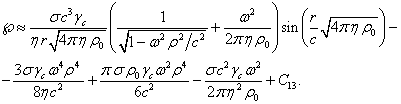. (44)

. (45)

Чтобы найти , можно в (44) положить угловую скорость вращения равной и результат сравнить с (36) для случая не вращающейся сферы. Это даёт:

. (46)

С другой стороны, в [27] были найдены следующие выражения:

, , . (47)

Отсюда следует, что скалярный потенциал поля давления в центре сферы выражается через среднеквадратичную скорость частиц в центре сферы:

, (48)

При этом в (46) будет:

. (49)

С учётом (46-49) выражения (44-45) запишутся так:

(50)

. (51)

При малых потенциал поля давления (51) вращающегося цилиндра перестаёт зависеть от и становится приблизительно равным .

5. Векторный потенциал поля давления

Подставляя в (35) фактор Лоренца вместо , получаем уравнение для векторного потенциала поля давления для случая вращения цилиндра без учёта собственного движения частиц вещества:

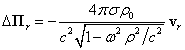. (52)

Скорость движения частиц в (52) определяется в (23). Поскольку (52) по своей форме совпадает с уравнением (22), то решением (52) для компоненты потенциала вдоль оси является выражение, повторяющее (26):

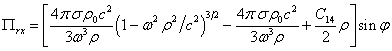. (53)

Согласно (39), скалярный потенциал поля давления прямолинейно движущейся частицы равен , а векторный потенциал должен равняться величине . Для скалярного потенциала и компоненты векторного потенциала в случае малых угловых скоростей вращения цилиндра это с учётом (23) и можно записать в следующем виде:

, .

Сравнивая с (51) при малых и , находим оценку отношения , что позволяет с учётом (47) уточнить выражение для :

, . (54)

Приравнивая в (53) и (54) при малых и , находим постоянную и уточняем выражение для :

.

.

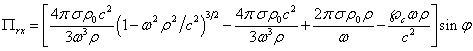Отсюда с учётом (23) векторный потенциал поля давления вращающегося цилиндра будет равен:

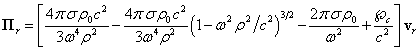. (55)

При этом векторный потенциал направлен вдоль линейной скорости и при малых угловых скоростях становится равным . Вблизи оси вращения, где , с учётом (47) будет .

По аналогии с (31), умножим на , чтобы учесть вклад собственного движения частиц в векторный потенциал поля давления вращающейся сферы:

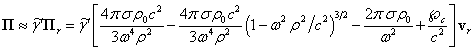. (56)

Согласно (30), величина близка к единице даже для нейтронной звезды.

6. Инвариантная масса всех частиц

Суммарная инвариантная масса частиц релятивистской однородной системы без общего вращения определяется формулой [18]:

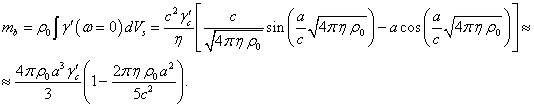
Если же рассматриваемая система вращается с угловой скоростью , то для вычисления инвариантной массы всех частиц системы следует использовать усреднённый фактор Лоренца , являющийся следствием (4). С учётом (5) и выражения для элемента движущегося за счёт вращения объёма имеем в сферических координатах:

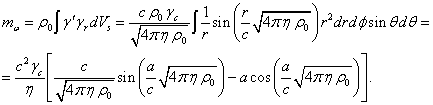
Поскольку суммарная инвариантная масса не зависит от характера движения частиц, то массы и должны равняться друг другу. Отсюда следует связь между факторами Лоренца в центре сферы: .

Это означает, что в принятом нами приближении частицы в центре сферы во вращающейся системе отсчёта двигаются с теми же скоростями, что и в случае системы частиц без общего вращения.

7. Заключение

Волновые уравнения (3) поля ускорений содержат скалярный потенциал и векторный потенциал , которые зависят от фактора Лоренца и от скорости движения частиц вещества. В общем случае частицы движутся хаотически с фактором Лоренца (5) и одновременно участвуют в коллективном движении, например, в общем вращении с фактором Лоренца (6). В результате фактор Лоренца становится зависимым от и от . При этом возникает необходимость усреднять величину для типичных частиц системы, с целью последующего использования в волновых уравнениях для потенциалов (7-8).

В дополнение к скалярному потенциалу (10) поля ускорений для неподвижной в целом системы частиц сферической формы, мы нашли выражения для скалярного потенциала в двух других случаях. Один из этих случаев предполагает вращение бесконечно длинного цилиндра, в котором пренебрегают собственным движением частиц вещества. Скалярный потенциал выражается при этом формулой (20). Другой случай описывает вращение вещества сферы с угловой скоростью , причём система частиц является релятивистской однородной системой. То, что собственное хаотическое движение частиц вносит свой вклада в скалярный потенциал вращающейся системы частиц, отражено в формуле (21).

Потенциал в отсутствие вращения, когда , переходит в потенциал неподвижной системы. Что касается векторного потенциала (31) поля ускорений, то он превышает векторный потенциал (29) цилиндра на небольшой по величине коэффициент согласно (30).

Рассмотренный подход полностью применим к полю давления с тем исключением, что скалярный потенциал поля ускорений по величине близок к квадрату скорости света, а скалярный потенциал поля давления в центре системы согласно (48) составляет приблизительно 1/3 квадрата среднеквадратичной скорости частицы.

Если использовать определение скалярного потенциала поля давления в (39), то для потенциала в центре сферы можно записать: , где и обозначают давление и плотность движущегося в центре вещества [27]. Сравнивая это с (48), приходим к релятивистской формуле для давления в центре неподвижной сферы, переходящую при малых скоростях в формулу из молекулярно-кинетической теории: 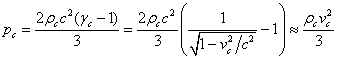. Здесь и есть среднеквадратичная скорость частиц вещества и соответственно фактор Лоренца в центре сферы.

С другой стороны, из (10), (36) и (47-48) следует соотношение:

,

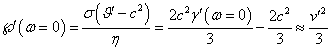так что скалярный потенциал поля давления в некоторой точке внутри неподвижной сферы в три раза меньше, чем квадрат скорости движения типичных частиц в этой точке.

Из (21) и (50) получается подобное соотношение 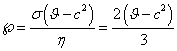, связывающее потенциалы поля давления и поля ускорений в веществе вращающейся сферы. Ранее подобные связи между потенциалами поля ускорений и поля давления были неизвестны.

Теперь, после вычисления скалярных и векторных потенциалов поля ускорений и поля давления, становится возможным определить напряжённости и соленоидальные векторы этих полей по формулам (2) и (34). В свою очередь, напряжённости и соленоидальные векторы данных полей требуются для задания уравнения движения вещества и вычисления релятивисткой энергии вращающегося тела с учётом энергии не только частиц, но и самих полей. Тем самым можно будет найти все важнейшие параметры системы. Такую работу планируется осуществить в следующей статье.

В качестве примера возьмём найденный нами скалярный потенциал и векторный потенциал поля ускорений, подставим эти потенциалы в (2) и получим векторы и . Ускорение типичной частицы в пределе специальной теории относительности будет определяться по формуле [19]:

, (57)

где есть скорость частицы.

Сравним теперь ускорение в (57) с формулой для ускорения частицы, представленной в [28, Eq. (5) ]:

. (58)

Как видно, потенциал совпадает по смыслу с потенциалом в (58), однако векторные потенциалы и имеют разный смысл. Вероятно это связано с тем, что (57) получается ковариантным образом из принципа наименьшего действия для непрерывных переменных, тогда как величины в (58) представлены в рамках дискретной классической механики, путём использования разложения Ходжа-Гельмгольца для ускорения.

Стандартное уравнение гидромеханики идеальной жидкости (уравнение Эйлера с учётом массовых сил) выглядят следующим образом:

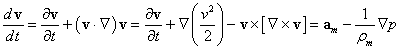, (59)

где есть скорость частиц жидкости; – ускорение от массовых сил, действующих в веществе; – плотность вещества; – давление.

Если обозначить и применить к обоим частям уравнения (59) операцию ротора, получается уравнение Фридмана, часто применяемое для вращательного движения:

. (60)

В простейшем случае, когда скорость лежит в плоскостях, параллельных плоскости системы координат, а угловая скорость вращения направлена вдоль оси и постоянна в каждой точке системы, будет . Уравнения (59) и (60) подразумевают, что вязкость и теплопроводность в жидкости отсутствуют и движение происходит адиабатически без изменения энтропии. Кроме этого, давление рассматривается как скалярное поле и потому участвует в образовании силы только лишь через градиент в виде члена . Путём решения уравнений движения (59) и (60) находится либо скорость , либо , если известны ускорение , плотность и давление как функции координат и времени.

В отличие от этого, гораздо более общий подход теории поля даёт следующее уравнение движения с учётом поля ускорений, векторного поля давления и поля диссипации [15], [19]:

. (61)

Здесь – 4-ускорение, выражаемое через тензор поля ускорений; – массовый 4-ток; – зарядовый 4-ток; , , и представляют собой тензоры соответственно гравитационного поля, электромагнитного поля, поля давления и поля диссипации. Указанные тензоры определяются через напряжённости и соленоидальные векторы. Так, компонентами тензора являются векторы и в (1-2), находимые через потенциалы поля ускорений, а компонентами тензора являются векторы и в (32-34), находимые через потенциалы поля давления. Уравнение движения вещества согласно (61) в пределе специальной теории относительности записывается так:

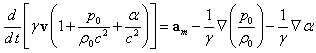. (62)

где есть фактор Лоренца; – функция диссипации, связанная со скалярным потенциалом поля диссипации соотношением ; – ускорение от массовых гравитационных и электромагнитных сил, действующих в веществе. Согласно [25], [27], можно записать следующее: , где есть скалярный потенциал поля давления.

Сравнение (62) и (59) обнаруживает различие, связанное с учётом релятивистских эффектов. Так, в (62) учтён фактор Лоренца , а также вклад инвариантного давления , инвариантной плотности массы и функции диссипации в левой части равенства. Кроме того, в правой части (62) находится под знаком градиента , тогда как в (59) величина находится за пределами градиента.

Уравнение (61) может быть записано не через тензоры, а непосредственно через 4-потенциалы полей [24]:

, (63)

. (64)

Здесь , и обозначают векторные потенциалы гравитационного поля, поля давления и электромагнитного поля, соответственно; есть плотность заряда произвольной частицы в сопутствующей ей системе отсчёта; индекс пробегает значения 0, 1, 2, 3; индекс пробегает значения 1, 2, 3; в декартовых координатах 4-радиус частицы ; , и обозначают 4-потенциалы гравитационного поля, поля давления и электромагнитного поля, соответственно; , и есть скалярные потенциалы гравитационного поля, поля давления и электромагнитного поля, соответственно.

В случае необходимости в (63-64) аналогичным образом могут быть учтены и другие векторные поля, например, поле диссипации. Уравнение (63) описывает баланс энергии в системе, а уравнение (64) есть уравнение движения вещества. Таким образом, если в системе решены волновые уравнения для потенциалов полей, подобные уравнениям (33) для поля давления, то с помощью этих потенциалов может быть найдено движение энергии и частиц в уравнениях (63-64). Указанный подход хорошо зарекомендовал себя, например, при решении типичных задач в электродинамике.

Ссылки на полученные в настоящей статье формулы для скалярных и векторных потенциалов полей приведены в Таблице 1.

Таблица 1. Указатель формул для потенциалов полей

	Неподвижная сферическая релятивистская система	Вращающаяся цилиндрическая система без учёта собственного движения частиц	Вращающаяся сферическая релятивистская система
Скалярный потенциал поля ускорений	(10)	(20)	(21)
Векторный потенциал поля ускорений		(29)	(31)
Скалярный потенциал поля давления	(36)	(51)	(50)
Векторный потенциал поля давления		(55)	(56)

Список использованных источников

1. Seung-Jae Lee, Jun-Hyeok Lee, Jung-Chun Suh. Computation of Pressure Fields around a Two-Dimensional Circular Cylinder Using the Vortex-In-Cell and Penalization Methods. Modelling and Simulation in Engineering, Vol. 2014, Article ID 708372, 13 pages (2014). https://doi.org/10.1155/2014/708372.

2. Dynnikova G. Ya. The Integral Formula for Pressure Field in the Nonstationary Barotropic Flows of Viscous Fluid. Journal of Mathematical Fluid Mechanics. Vol. 16, pp. 145–162 (2014). https://doi.org/10.1007/s00021-013-0148-z.

3. Gunaydinoglu E., Kurtulus D.F. Pressure-velocity coupling algorithm-based pressure reconstruction from PIV for laminar flows. Experiments in Fluids, Vol. 61, Issue 1, article id.5 (2019). https://doi.org/10.1007/s00348-019-2831-1.

4. Pan H., Williams S H., Krueger P. S. Determination of the Pressure Field Using Three-Dimensional, Volumetric Velocity Measurements. Journal of Fluids Engineering, Vol. 138 (8), 084502 (9 pages) Aug 2016. https://doi.org/10.1115/1.4033293.

5. Aldo Bressan. Relativistic Theory of Materials. Springer-Verlag, Berlin, Heidelberg (1978). ISBN 978-3-642-81122-7. https://doi.org/10.1007/978-3-642-81120-3.

6. Griffiths D. J. (2007) Introduction to Electrodynamics,
3rd Edition; Prentice Hall - Problem 5.29.

7. Redzic D.V. Electromagnetostatic charges and fields in a rotating conducting sphere. Progress In Electromagnetics Research, Vol. 110, pp. 83-401 (2010). http://dx.doi.org/10.2528/PIER10100504.

8. Gron O. and Voyenli K. Charge distributions in rotating conductors. European Journal of Physics, Vol. 3, Number 4, pp. 210-214 (1982). https://doi.org/10.1088/0143-0807/3/4/004.

9. Marsh J.S. Magnetic and electric fields of rotating charge distributions. American Journal of Physics, Vol. 50, Issue 1, pp. 51-53 (1982). https://doi.org/10.1119/1.13006.

10. Marsh J.S. Magnetic and electric fields of rotating charge distributions II. American Journal of Physics, Vol. 52, Issue 8, pp. 758-759 (1984). https://doi.org/10.1119/1.13852.

11. Healy W.P. Comment on ‘The effect of radial acceleration on the electric and magnetic fields of circular currents and rotating charges’. J. Phys. A: Math. Gen. Vol. 35, pp. 2527-2531 (2002). https://doi.org/10.1088/0305-4470/35/10/403.

12. Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003. // Четырёхмерное уравнение движения вязкого сжимаемого заряженного вещества с учётом поля ускорений, поля давления и поля диссипации.

13. Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593. // Оценка физических параметров планет и звёзд в модели гравитационного равновесия.

14. Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8. // Теорема вириала и кинетическая энергия частиц макроскопической системы в концепции общего поля.

15. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947. // Калибровка энергии и метрики в ковариантной теории гравитации .

16. Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics (2018). http://dx.doi.org/10.1007/s00161-018-0715-x. // Интегральная теорема обобщённого вириала в релятивистской однородной модели.

17. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi: 10.11648/j.ajmp.20140304.12; Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

18. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого поля.

19. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304. // О космологической постоянной, поле ускорения, поле давления и об энергии.

20. Fedosin S.G. The electromagnetic field in the relativistic uniform model. International Journal of Pure and Applied Sciences, Vol. 4, Issue. 2, pp. 110-116 (2018). http://dx.doi.org/10.29132/ijpas.430614. // Электромагнитное поле в релятивистской однородной модели .

21. Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39. // Гравитационное поле в релятивистской однородной модели в рамках ковариантной теории гравитации.

22. Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197. // Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.

23. Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357. // Заряженная компонента вакуумного поля как источник электрической силы в модернизированной модели Лесажа.

24. Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в теории релятивистских векторных полей.

25. Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101. // Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.

26. Ландау Л.Д., Лифшиц Е.М. Статистическая физика. – 5-е издание. – М.: ФИЗМАТЛИТ, 2002. – 616 с. – («Теоретическая физика», том V).

27. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06. // Энергия связи и полная энергия макроскопического тела в релятивистской однородной модели.

28. Caltagirone J.P., Vincent S. On primitive formulation in fluid mechanics and fluid–structure interaction with constant piecewise properties in velocity–potentials of acceleration. Acta Mech. Vol. 231, pp. 2155-2171 (2020). https://doi.org/10.1007/s00707-020-02630-w.

Источник: http://sergf.ru/paf.htm

На научный сайт