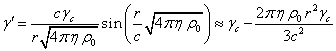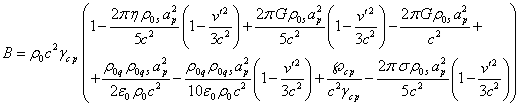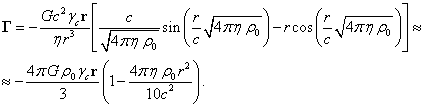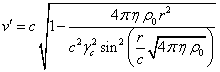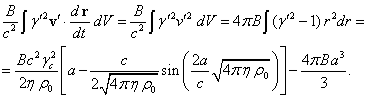In English

Continuum Mechanics and Thermodynamics (2018). http://dx.doi.org/10.1007/s00161-018-0715-x.

Интегральная теорема обобщённого вириала в релятивистской однородной модели

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail fedosin@hotmail.com

В релятивистской однородной модели для сплошной среды выводится интегральная теорема обобщённого вириала, в которой в качестве импульсов частиц используются обобщённые импульсы. Это позволяет найти точные формулы для радиальной компоненты скорости типичных частиц системы и для их среднеквадратичной скорости, не используя понятия температуры. Показывается связь теоремы с космологической постоянной, характеризующей рассматриваемую физическую систему. Объясняется различие между кинетической энергией, и энергией движения, значение которой равняется половине суммы лагранжиана и гамильтониана. Данное различие связывается с тем, что собственные поля каждой частицы обладают массой-энергией, делающей дополнительный вклад в кинетическую энергию. В результате получается суммарная энергия движения частиц и полей.

Ключевые слова: теорема обобщённого вириала; релятивистская однородная модель; космологическая постоянная; энергия движения; кинетическая энергия.

The integral theorem of generalized virial in the relativistic uniform model

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

e-mail fedosin@hotmail.com

In the relativistic uniform model for continuous medium the integral theorem of generalized virial is derived, in which generalized momenta are used as particles’ momenta. This allows us to find exact formulas for the radial component of the velocity of typical particles of the system and for their root-mean-square speed, without using the notion of temperature. The relation between the theorem and the cosmological constant, characterizing the physical system under consideration, is shown. The difference is explained between the kinetic energy and the energy of motion, the value of which is equal to half the sum of the Lagrangian and the Hamiltonian. This difference is due to the fact that the proper fields of each particle have mass-energy, which makes an additional contribution into the kinetic energy. As a result, the total energy of motion of particles and fields is obtained.

Keywords: generalized virial theorem; relativistic uniform model; cosmological constant; energy of motion; kinetic energy.

1. Введение

В теоретической физике теорема вириала представляет собой соотношение, связывающее между собой кинетическую энергию и другие виды энергии в системе из частиц и полей. Существуют различные модификации теоремы, в том числе в классической механике [1], в аналитической лагранжевой механике [2] и в квантовой механике [3]. Как правило используется векторная запись теоремы, но возможны и тензорные варианты [4].

Ранее мы изучали применение теоремы вириала в релятивистской однородной системе, состоящей из частиц, удерживаемых собственными полями [5]. При этом получилось отличие от классического случая, достигающее величины 20 %. Причиной такому положению дел оказалось неравенство нулю вычисленной нами конвективной части временной производной вириальной функции системы, усреднённой по времени.

Теперь мы хотим рассмотреть теорему не обычного, а обобщённого вириала в релятивистской однородной модели, и применить те возможности, которые она предоставляет. В частности, нам удастся найти точные формулы для радиальной компоненты скорости частиц внутри системы и для среднеквадратичной скорости, а так же понять различие между кинетической энергией и энергией движения частиц, связанной с их обобщёнными импульсами.

2. Теорема обобщённого вириала

Обобщённую вириальную функцию мы определяем следующим образом:

, (1)

где есть обобщённый 3-импульс произвольной частицы системы; есть 3-вектор местоположения частицы с номером , данный вектор входит в число возможных обобщённых координат; задаёт число частиц в системе.

Следует заметить, что в обобщённый импульс частицы вносят вклад все поля, связанные с данной частицей и влияющие на неё. Мы используем обобщённые импульсы в (1) потому, что в замкнутой системе сохраняется сумма именно таких импульсов частиц [6]. В противоположность этому, в обычной формулировке теоремы вириала вместо в (1) стоит импульс частицы с номером , находимый через массу и скорость частицы.

В рассматриваемом случае обобщённая 3-скорость частицы задаётся выражением . Для непрерывно распределённых систем из (1) видно, что изменение обобщённой вириальной функции относительно некоторого центра может сопровождаться как изменением импульсов частиц, так и некоторым изменением формы системы.

Возьмём временную производную от вириальной функции (1):

. (2)

По стандартной процедуре необходимо ещё осуществить временное усреднение всех членов в равенстве (2) за достаточно большой промежуток времени. Во многих практических случаях левая часть (2) стремится или близка к нулю, что приводит к связи между двумя членами в правой части. По порядку величины сумма , где 3-вектор есть обобщённая сила, равна потенциальной энергии взаимодействия частиц в случае потенциальных сил, а сумма приблизительно равна удвоенной кинетической энергии . При этих предположениях из (2) следует классическая теорема вириала:

. (3)

3. Релятивистская однородная система

Релятивистская однородность подразумевает, что инвариантная плотность, или плотность массы (заряда) в системах отсчёта, сопутствующих частицам, является постоянной для всех частиц.

Пусть имеется сферическая система из таких тесно взаимодействующих частиц, связанных друг с другом посредством гравитационного и электромагнитного полей. Мы будем использовать ещё концепцию векторного поля давления, а также концепцию векторного поля ускорений, в которой роль тензора энергии-импульса вещества играет тензор энергии-импульса поля ускорений [7, 8]. Все эти четыре поля являются векторными, могут быть построены по единому образцу и имеют собственные 4-потенциалы, а значит и соответствующие скалярные и векторные потенциалы.

Для случая, когда частицы настолько тесно взаимодействуют друг с другом, что практически сливаются и образуют непрерывно распределённое вещество, в качестве репрезентативных единиц вещества берутся так называемые типичные частицы. Уравнения движения применяются именно к типичным частицам, а все физические величины также записываются в применении к типичным частицам. Предполагается, что типичные частицы в среднем характеризуют вещество во всех отношениях. Для типичных частиц непрерывно распределённого вещества удобно переписать (1) через интеграл по объёму, используя результаты в [7]:

, (4)

,

где – скорость света; – инвариантная плотность массы; – инвариантная плотность заряда; , , и представляют собой векторные потенциалы поля ускорений, гравитационного поля, электромагнитного поля и поля давления соответственно, – временная компонента 4-скорости частицы.

В (4) символ обозначает интеграл по объёму одной движущейся типичной частицы, а символ предполагает суммирование по всем частицам.

Рассмотрим далее приближение слабого поля, когда искривлением пространства-времени можно пренебречь и рассматривать ситуацию в плоском пространстве-времени Минковского в рамках специальной теории относительности. В этом случае детерминант метрического тензора равен , а элемент ковариантного объёма заменяется на элемент обычного трёхмерного объёма .

Соответственно, величина в (4) будет временной компонентой средней 4-скорости частиц, находящихся на текущем радиусе , причём фактор Лоренца частиц внутри сферы согласно [9] оказывается функцией текущего радиуса:

. (5)

Здесь есть коэффициент поля ускорений, – фактор Лоренца для скорости частиц в центре сферы, и ввиду малости аргумента синус может быть разложен до членов второго порядка.

Для упрощения дальнейших расчётов будем считать, что частицы в рассматриваемой системе движутся хаотично без общего вращения и направленных потоков вещества. В этом случае глобальные векторные потенциалы каждого поля обнуляются, поскольку векторная сумма потенциалов в произвольной точке стремится к нулю из-за разного направления векторных потенциалов отдельных частиц. У каждой из частиц остаются лишь собственные векторные потенциалы, происходящие от движения их собственных внутренних полей.

Поэтому в (4) вместо , , и следует подставить малые по величине собственные векторные потенциалы , , и , которые обратно пропорциональны квадрату скорости света и прямо пропорциональны скоростям частиц и скалярным потенциалам , , и внутренних собственных полей частиц. Действуя аналогично [5], в приближении прямолинейного движения частиц без ускорения, типичного для специальной теории относительности, имеем:

, ,

, . (6)

Скалярные потенциалы , , и поля ускорений, гравитационного и электромагнитного полей, и поля давления, соответственно, являются потенциалами в системе отсчёта центра импульсов каждой частицы. Мы можем считать, что если частицы содержат внутри себя хаотически движущееся вещество и сами представляют собой релятивистские однородные системы, в них нет внутренних глобальных векторных потенциалов. Но для наблюдателя, неподвижного относительно сферы, частицы движутся и он регистрирует внутри частиц как скалярные потенциалы , , и , так и векторные потенциалы (6). Подстановка (6) в (4) в рамках специальной теории относительности даёт:

. (7)

Как было показано в [9, 10], в первом приближении скалярные потенциалы полей внутри релятивистской однородной системы зависят лишь от квадрата радиуса. В применении к отдельной частице их можно выразить так:

, ,

, , (8)

где – фактор Лоренца движения субчастиц внутри частицы, записываемый аналогично (5); – фактор Лоренца в центре частицы; – инвариантная плотность массы субчастиц; – текущий радиус внутри частицы; – гравитационная постоянная; – радиус частицы; – электрическая постоянная; – инвариантная плотность заряда субчастиц; – скалярный потенциал поля давления в центре частицы; – коэффициент поля давления.

Элемент объёма в (7) есть элемент объёма неподвижной сферы. В первом приближении мы можем считать, что является также элементом движущегося объёма частицы, тогда сумма таких объёмов по всем частицам должна давать объём сферы. Поэтому интеграл в (7) можно считать интегралом по движущемуся объёму частицы с номером .

Пусть движущаяся частица в начальный момент времени пересекает начало неподвижной системы отсчёта, двигаясь с постоянной скоростью вдоль оси . Действуя далее согласно [11] и приложения A в [10], выразим координаты внутри частицы с точки зрения неподвижной системы отсчёта через сферические координаты в системе центра импульсов частицы:

, , . (9)

Скалярные потенциалы в (8) зависят от текущего радиуса, для которого с учётом (9) можно записать:

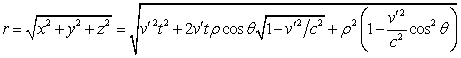. (10)

Элемент движущегося объёма частицы в сферических координатах (9) определяется формулой , где есть определитель матрицы якобиана:

.

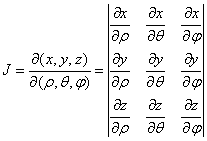Определяя с учётом (9), находим элемент объёма . В результате в (7) для интеграла по объёму движущейся частицы имеем:

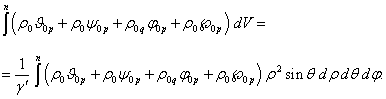(11)

В силу релятивистского эффекта сокращения длины при движении, объём движущейся частицы становится эллипсоидом Хевисайда. Из преобразований Лоренца следует уравнение поверхности такого эллипсоида:

. (12)

После подстановки (9) в (12) становится видно, что координата при интегрировании в (11) должна меняться от до радиуса частицы , а углы и меняются так же, как и в сферических координатах (от 0 до для угла , и от 0 до для угла ).

Подставляя (10) в (8), а (8) в (11), при находим:

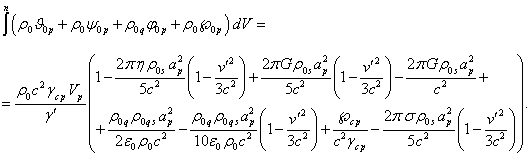
(13)

Здесь есть инвариантный объём частицы. Скобка в (13) зависит от радиуса частицы , а также от отношения .

Это отношение мало в большинстве случаев, когда скорость частицы значительно меньше скорости света. Если сделать обозначение

.

(14)

то (13) можно сокращённо записать так:

.

Подстановка этого в (7) даёт:

.

Перейдём в данном выражении от суммы по частицам к интегралу по объёму сферы, считая, что элементом объёма сферы является частное от деления инвариантного объёма частицы на фактор Лоренца . В первом приближении можно также считать, что величина постоянна и одинакова для всех частиц, и тогда её можно вынести за знак интеграла:

. (15)

Возьмём производную по времени от в (15) таким образом, чтобы появилась величина :

. (16)

4. Расчёт для соотношения (16)

Как и в [5], производную по времени внутри интеграла в левой части (16) будем рассматривать как субстанциальную производную:

. (17)

Так как мы должны везде брать средние величины для типичных частиц, соотношение следует рассматривать статистически, считая, что амплитуды отдельных членов равны друг другу, то есть . Тогда в первом приближении можно считать, что , где есть усреднённая радиальная компонента скорости . При этом все переменные будут зависеть только от радиальной координаты , так что , а также . С учётом (17) для левой части (16) в сферических координатах, в которых , можно записать:

. (18)

В правой части (16) содержится следующая производная по времени:

.

Так как фактор Лоренца выражается через квадрат скорости , то будет справедливо соотношение . Учитывая ещё соотношения , и , для первого интеграла правой части (16) в сферических координатах находим:

. (19)

В рассматриваемой системе ввиду хаотичности движения частиц близки к нулю как глобальные векторные потенциалы полей, так и соответствующие соленоидальные векторы, включая поле гравитационного кручения , индукцию магнитного поля и соленоидальный вектор поля давления . В этом случае силы Лоренца отсутствуют и аналогично [7] плотности сил в уравнении движения частиц зависят только от напряжённостей полей:

. (20)

Уравнение (20) справедливо в приближении специальной теории относительности, при этом движение типичных частиц аппроксимируется прямолинейным движением без собственного вращения частиц.

Напряжённости электрического поля, гравитационного поля и поля давления внутри сферы, действующие на типичные частицы, были найдены в [9]:

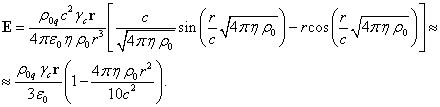
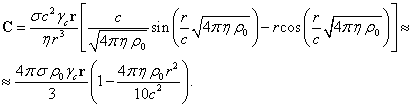
Подставим данные выражения для напряжённостей полей в (20):

. (21)

При выводе (21) было использовано соотношение между коэффициентами полей, полученное в [12] с помощью уравнения движения и обобщённой теоремы Пойнтинга:

. (22)

Подстановка (21) во второй интеграл в правой части (16) в сферических координатах даёт следующее:

.

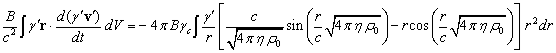(23)

5. Радиальная компонента скорости

Подставим (18), (19) и (23) в (16), сократим одинаковые множители, уберём интегралы и после вычитания одинаковых членов получим:

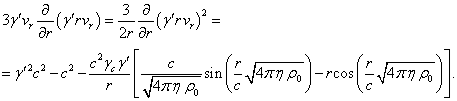
Данное равенство представляет собой дифференциальное уравнение для нахождения . Подставим в правую часть равенства из (5):

.

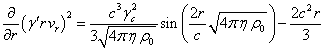Решая данное уравнение с учётом (5), находим его решение:

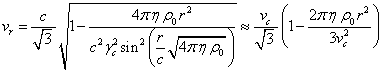. (24)

Приблизительное решение в правой части (24) получается при разложении синуса до членов второго порядка и с учётом равенства 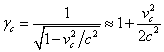для фактора Лоренца и скорости частиц в центре сферы.

Ранее мы уже оценивали радиальную компоненту скорости в [5]:

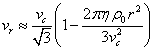. (25)

Коэффициент в (25) был следствием предположения, что в среднем все ортогональные друг другу компоненты скорости типичной частицы в сферических координатах имеют одинаковую амплитуду, то есть . Из сравнения (24) и (25) следует, что в (24) формула для величины радиальной скорости частиц получена нами с более высокой точностью.

Учитывая, что , , с помощью (5) можно найти среднеквадратичную скорость типичных частиц внутри сферы:

. (26)

Сравнивая и в (24), находим, что , что как раз соответствует предположению равенства амплитуд компонент скоростей .

Заметим, что для идеального газа стандартным способом определения среднеквадратичной скорости частиц является использование распределения Максвелла, когда скорость связывается с массой частиц , температурой и постоянной Больцмана :

. (27)

Если приравнять (26) и (27), то видно, что в центре системы температура должна быть максимальна.

В кинетической теории газов скорость звука выражается через показатель адиабаты (Heat capacity ratio) , где и означают удельные теплоёмкости при постоянном давлении и постоянном объёме, соответственно; есть число степеней свободы частицы газа [13]:

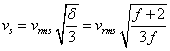. (28)

С помощью скорости звука в (28) можно экспериментально оценить среднеквадратичную скорость в разных точках системы и сравнить её с (27). В свою очередь, сравнение со скоростью в (26) даёт возможность оценить коэффициент поля ускорений .

6. Уравнение движения

С помощью радиальной компоненты скорости типичных частиц (24) можно проверить, как выполняется уравнение движения (20). Спроектируем это уравнение на радиальное направление. Проекция правой части (20) согласно (21) будет равна:

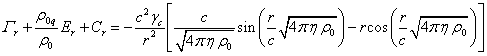. (29)

Проекция левой части (20) на радиальное направление с учётом преобразования , использованного при выводе (18), и с учётом (5) и (24) приобретает следующий вид:

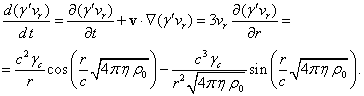
Из равенства данного выражения и (29) следует, что (24) согласуется с уравнением движения.

7. Количественные соотношения в теореме обобщённого вириала

Аналогично (2) возьмём производную по времени от величины в (15):

. (30)

Вычислим каждый член в (30) и затем сравним эти члены друг с другом. Для левой части (30) с учётом (18), (24) и (5) находим:

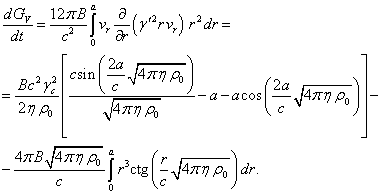(31)

Преобразуем подынтегральное выражение в правой части (30) с помощью (21) и равенств и :

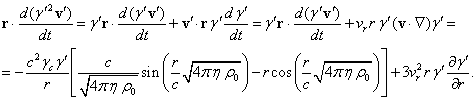
С учётом этого и соотношений (5) и (24) для первого интеграла в правой части (30) в сферических координатах получим:

(32)

Вычислим последний интеграл в правой части (30) с помощью (5) и соотношения :

(33)

Если подставить (31), (32) и (33) в (30), то все члены сокращаются без остатка, что подтверждает правильность наших расчётов. Разложим теперь в (31), (32) и (33) периодические функции до членов, содержащих в знаменателе . Затем используем приблизительное выражение для фактора Лоренца через квадрат скорости частиц в центре сферы согласно [5]:

, (34)

где есть произведение плотности массы на объём сферы с радиусом .

Это даёт следующее:

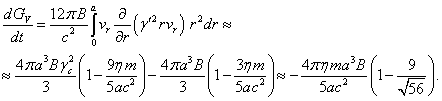(35)

. (36)

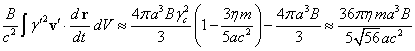. (37)

Согласно (14), , что даёт для (37) следующее:

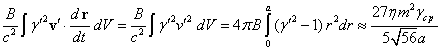. (38)

По своему смыслу энергия в (37) и (38) соответствует энергии в (2) и представляет собой удвоенную энергию движения , как это было определено в [14]. При этом равно по величине сумме лагранжиана и гамильтониана. Таким образом, .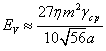

Согласно интегральной теореме обобщённого вириала (30), соотношение (35) есть сумма соотношений (36) и (37). Мы видим, что временная производная вириальной функции в (35) не равна нулю. Считая, что энергия (36) есть потенциальная энергия , связанная с обобщёнными силами внутри системы, а энергия (37) равна , для связи между этими энергиями находим:

. (39)

Полученное нами соотношение (39) между энергиями отличается от классической теоремы вириала (3) и при этом точно совпадает с соотношением между энергиями в [5], где исследовалась релятивистская теорема вириала с учётом четырёх полей. Таким образом, теорема обобщённого вириала даёт такой же результат, что и релятивистская теорема вириала.

Кинетическая энергия частиц рассматриваемой системы была найдена в [5] в следующем виде:

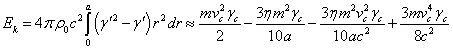. (40)

Если подставить сюда из (34), кинетическая энергия в первом приближении выразится так:

.

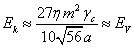Отсюда следует, что в рассматриваемой системе кинетическая энергия того же порядка, что и энергия движения . Такое совпадение будет справедливо до тех пор, пока скорость движения частиц остаётся малой по сравнению со скоростью света, а факторы Лоренца и близки к единице. Однако в общем случае , поскольку согласно (38) и (40)

. (41)

8. Заключение

В отличие от стандартной теоремы вириала, теорема обобщённого вириала имеет дело с обобщёнными импульсами частиц. Мы используем обобщённые импульсы потому, что именно сумма таких импульсов сохраняется в замкнутой системе, как это следует из лагранжевой механики. В рассматриваемой релятивисткой однородной системе глобальные векторные потенциалы полей равны нулю ввиду хаотического движения частиц. Поэтому обобщённые импульсы частиц включают в себя только собственные векторные потенциалы полей, возникающие за счёт движения частиц.

Поскольку временная производная вириальной функции (30) оказывается не равной нулю, вместо (3) выполняется соотношение в (39), и доля энергии движения частиц по отношению к модулю потенциальной энергии, связанной с обобщёнными силами, увеличивается по сравнению с классическим случаем. Полученные нами результаты в целом совпадают с теми, которые были найдены в [5] для обычной теоремы вириала в релятивистской форме.

Мы показываем, что производная по времени от обобщённой вириальной функции не равна нулю благодаря зависимости этой функции от текущего радиуса. Производная по времени в таком случае должна рассматриваться как материальная производная, включающая в себя конвективную производную. При этом в результате усреднения величин в конвективной производной мы можем сделать замену вида , и тем самым использовать в формулировке теоремы радиальную компоненту скорости частиц . Это даёт возможность найти формулу для вычисления в (24) и затем проверить её в уравнении движения типичных частиц.

Представленная в (26) формула определяет среднеквадратичную скорость типичных частиц в каждой точке системы через текущий радиус и параметры частиц, и выводится с помощью теории поля. Это существенно отличает от среднеквадратичной скорости (27), выражаемой через температуру, и от скорости звука в (28), находимых статистическими методами. Так как среднеквадратичная скорость не должна зависеть от способа её определения, сочетание формул (26-28) позволяет найти новые связи между параметрами частиц и термодинамическим параметрами.

В (38) и (39) мы находим энергию движения , которая по своей величине достаточно близка к кинетической энергии в (40). Чтобы понять различие между этими энергиями, обратимся к условию калибровки релятивистской энергии согласно [7] и [10]:

, (42)

где ; есть гравитационная постоянная; есть константа порядка единицы, входящая как множитель в уравнение для метрики; есть космологическая постоянная; , , и представляют собой 4-потенциалы для поля ускорений, гравитационного поля, электромагнитного поля и поля давления соответственно; , , и – скалярные потенциалы соответственно поля ускорений, гравитационного и электромагнитных полей и поля давления.

При выполнении условия (42) релятивистская энергия системы не зависит ни от скалярной кривизны, ни от космологической постоянной, и становится однозначно определённой. В (42) космологическая постоянная выражается через сумму произведений 4-потенциалов полей на 4-токи, при этом все действующие в системе поля считаются векторными. В частности, гравитационное поле рассматривается в рамках векторной ковариантной теории гравитации, которая в пределе слабого поля и малых скоростей переходит в Лоренц-инвариантную теорию гравитации, обобщающую теорию тяготения Ньютона на инерциальные системы отсчёта. Заметим, что в общей теории относительности гравитационное поле является тензорным полем, связанным с метрическим тензором. Это приводит к невозможности использования космологической постоянной для калибровки энергии аналогично (42), так как изменяется трактовка самой космологической постоянной. При этом становится невозможно ни локализовать однозначно гравитационную энергию в пространстве, ни вычислить энергию системы независимо от выбора системы отсчёта [15-17].

В рамках специальной теории относительности массовый 4-ток , зарядовый 4-ток , где есть 4-скорость. Условие калибровки энергии будет тогда выглядеть так:

. (43)

Предположим, что рассматриваемая нами сферическая система из частиц и полей образовалась из вещества, которое вначале было рассеяно на бесконечности и находилось там почти неподвижно, а затем было собрано в сферу действием гравитации. В начальном состоянии можно положить, что скорости частиц , тогда фактор Лоренца для всех частиц . Скалярные потенциалы полей при этом будут равны собственным потенциалам частиц, и для (43) имеем:

. (44)

Заметим теперь, что сумма членов в правой части (44) содержится в виде множителя в соотношениях (7), (11), (14), и во всех соотношениях, где присутствует величина . Таким образом космологическая постоянная рассматриваемой физической системы оказывается включённой в нашу формулировку интегральной теоремы обобщённого вириала.

Рассмотрим теперь принципиальное различие между кинетической энергией частиц и энергией движения , удвоенное значение которой приведено в (38) согласно [7]. Дело в том, что вместе с частицами передвигаются и их собственные поля, связанные с частицами. Эти поля имеют массу-энергию и следовательно, участвуют в образовании обобщённого импульса каждой частицы. Если есть кинетическая энергия одной частицы, то , однако энергия движения содержит ещё дополнительные вклады от массы-энергии полей частиц и потому не равна кинетической энергии . Можно также сказать, что кинетическая энергия учитывает только энергию поля ускорений, описывающего движение частиц, а добавка вклада от всех остальных полей приводит к энергии движения частиц и полей системы. Действительно, в (40) зависит от фактора Лоренца , находимого согласно (5) с помощью уравнений для поля ускорений. В то же время зависит от всех полей, так как определяется через полусумму лагранжиана и гамильтониана системы и кроме этого зависит от величины и членов в (44).

Неравенство между энергиями и в (41) определяется параметрами системы, однако между этими энергиями имеется связь, поскольку в рассматриваемой системе выполняется соотношение (22) для коэффициентов полей, а кинетическая и потенциальная энергии согласно [18] могут преобразовываться друг в друга.

Список использованных источников

1. Goldstein H. Classical Mechanics (2nd ed.). Addison–Wesley. (1980).

2. Ganghoffer J. and Rahouadj, R. On the generalized virial theorem for systems with variable mass. Continuum Mech. Thermodyn. Vol. 28, pp. 443-463 (2016). doi:10.1007/s00161-015-0444-3.

3. Fock V. Bemerkung zum Virialsatz. Zeitschrift für Physik A. Vol. 63 (11), pp. 855-858 (1930). doi:10.1007/BF01339281.

4. Parker E.N. Tensor Virial Equations. Physical Review. Vol. 96 (6), pp. 1686-1689 (1954). doi:10.1103/PhysRev.96.1686.

5. Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и кинетическая энергия частиц макроскопической системы в концепции общего поля.

6. Landau L.D. and Lifschitz E.M. Mechanics. Course of Theoretical Physics. Vol. 1 (3rd ed.). London: Pergamon. (1976). ISBN 0-08-021022-8.

7. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; О космологической постоянной, поле ускорения, поле давления и об энергии.

8. Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics. Vol. 8, pp. 771-779 (2014). doi: 10.12988/astp.2014.47101; Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.

9. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi: 10.11648/j.ajmp.20140304.12; Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

10. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого поля.

11. Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, Vol. 23, pp. 19-25 (2013). http://dx.doi.org/10.5281/zenodo.889383; Проблема 4/3 для гравитационного поля.

12. Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров планет и звёзд в модели гравитационного равновесия.

13. Reif F. Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc. (2009). ISBN 1-57766-612-7.

14. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023; Гамильтониан в ковариантной теории гравитации.

15. Дирак П.А.М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с. Dirac P.A.M. General Theory of Relativity (1975), Princeton University Press, quick presentation of the bare essentials of GTR. ISBN 0-691-01146-X.

16. Денисов, В.И.; Логунов А.А. Инертная масса, определенная в общей теории относительности, не имеет физического смысла. ТМФ, 1982, том 51, номер 2, 163-170; Denisov V.I., Logunov A.A. The inertial mass defined in the general theory of relativity has no physical meaning. Theoretical and Mathematical Physics, Volume 51, Issue 2, pp. 421-426 (1982). http://dx.doi.org/10.1007/BF01036205.

17. Khrapko R. I. The Truth about the Energy-Momentum Tensor and Pseudotensor. ISSN 0202-2893, Gravitation and Cosmology, Vol. 20, No. 4, pp. 264-273 (2014). Pleiades Publishing, Ltd., 2014. http://dx.doi.org/10.1134/S0202289314040082; Храпко Р.И. Правда о тензоре и псевдотензоре энергии-импульса.

18. Snider R.F. Conversion between kinetic energy and potential energy in the classical nonlocal Boltzmann equation. Journal of Statistical Physics, Vol. 80, pp. 1085-1117 (1995). https://doi.org/10.1007/BF02179865.

Источник: http://sergf.ru/it.htm

На научный сайт