Canadian
Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp. 5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206
О структуре силового поля в электрогравитационном вакууме
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Анализ уравнений поля для тензоров массовой и зарядовой компонент общего поля показывает, что их источником является зарядовый 4-ток. В связи с этим делается предположение о том, что именно зарядовая компонента силового поля электрогравитационного вакуума в виде потоков заряженных частиц в рамках гравитации Лесажа в основном ответственна как за электромагнитное, так и гравитационное взаимодействия, а также и за действие других полей внутри тел. Параметры вакуумных заряженных частиц могут быть определены достаточно точно с помощью теории подобия в теории бесконечной вложенности материи, так что описание причины возникновения электромагнитных и гравитационных сил наполняется конкретным содержанием.
Ключевые
слова: силовое поле;
электромагнитное взаимодействие; гравитационное взаимодействие; электрогравитационный вакуум.
On the
structure of the force field in electrogravitational vacuum
Sergey G. Fedosin
PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia
E-mail: fedosin@hotmail.com
Analysis of the field equations for the tensors of the mass and charge
components of the general field shows that their source is the charge
four-current. In this connection, an assumption is made that it is the charge
component of the force field of the electrogravitational vacuum in the form of
fluxes of charged particles within the framework of Le Sage's theory of
gravitation, which is mainly responsible for both electromagnetic and
gravitational interactions, as well as for the action of other fields inside
bodies. The parameters of the vacuum’s charged particles can be determined quite
accurately using the theory of similarity within the theory of infinite nesting
of matter, so that the description of the cause of emergence of electromagnetic
and gravitational forces is filled with specific content.
Keywords: force field; electromagnetic interaction; gravitational interaction; electrogravitational vacuum.
1. Введение
Концепция силового вакуумного поля берёт своё начало с момента появления модели Фатио-Лесажа в 17-18 веках, в которой многочисленные быстро движущиеся мельчайшие частицы, заполняющие всё пространство, пронизывают все тела и приводят к возникновению тяготения между телами [1-4]. Модернизированная модель Фатио-Лесажа не только описывает возникновение сил гравитации [5], но объясняет ещё происхождение электромагнитных сил [6]. Кроме этого, данная модель в соединении с теорией бесконечной вложенности материи представляет конкретные параметры частиц, множество которых составляет силовое поле электрогравитационного вакуума.
В частности, для частиц типа праонов вычисляется плотность энергии и плотность потока энергии, фактор Лоренца, предельная плотность переносимого электрического тока, сечение взаимодействия частиц с веществом. Праоны принадлежат нижележащему уровню материи и предполагается, что они соотносятся с нуклонами так же, как нуклоны соотносятся с нейтронными звёздами. В [7] определяется фактор Лоренца в центре протона, а последующее использование теории подобия позволяет оценить заряд праона, его массу и размеры, действующие на уровне материи праонов гравитационную постоянную, постоянную Дирака и постоянную Больцмана.
В результате действия силового вакуумного поля на вещество возникают явления электромагнетизма и гравитации, которые в современной физике описываются теорией поля. Одним из первых учёных, кто указал на аналогию уравнений электромагнитного и гравитационного полей, является Оливер Хэвисайд [8]. В результате гравитационное поле должно иметь две компоненты, так же как и электромагнитное поле, содержащее в себе электрическую и магнитную компоненты [9]. С учётом этого, в [10] рассматривается теория акустических волн, зависящих одновременно от потенциалов как электромагнитного, так и гравитационного полей, и распространяющихся в твёрдых телах. Теория гравитации, построенная аналогично теории электромагнитного поля, представлена в [11-13].
В общей теории относительности гравитационное поле рассматривается как тензорное метрическое поле, и фактически замещается метрикой пространства-времени, так что физика явлений скрыта в тени геометрии. В слабом поле уравнения общей теории относительности могут быть представлены как уравнения гравитоэлектромагнетизма, в которых гравитационное поле действительно описывается через две компоненты [14-18].
В отличие от этого, в ковариантной теории гравитации гравитационное поле является физически действующим векторным полем, существующим независимо от метрики. В результате гравитационное поле описывается собственным 4-потенциалом и тензором гравитационного поля, причём тензор энергии-импульса поля выводится из принципа наименьшего действия в ковариантном виде [19].
Для краткости мы будем рассматривать далее только четыре основных поля – гравитационное и электромагнитное поля, полей ускорений и поле давления. Все эти поля являются векторными полями, и в случае необходимости к ним можно добавить другие векторные поля, например, поле диссипации [20], поле слабого и поле сильного взаимодействий. Все эти поля могут быть объединены в одно общее поле [21]. В качестве физической модели, описывающей вещество, будет использоваться релятивистская однородная система, имеющая сферическую форму и находящуюся в равновесии под действием собственной гравитации и остальных трёх полей.
Нашей целью будет анализ теории общего поля и последующее определение основной действующей компоненты силового поля электрогравитационного вакуума. Это может быть важным для развития проектов получения энергии из вакуума и изготовления электрогравитационных двигателей [22-24].
2. Связи между 4-токами, тензорами полей и компонентами вакуумного поля
Уравнение движения вещества в двухкомпонентном общем
поле в ковариантном виде записывается следующим образом [25]:
. (1)
Здесь 
– тензор
электромагнитного поля, рассматриваемый как тензор зарядовой компоненты общего
поля; 
– 4-вектор зарядового тока; 
– плотность заряда типичной частицы вещества в
сопутствующей частице системе отсчёта; 
– 4-скорость частицы; 
– тензор массовой
компоненты общего поля; 
– 4-вектор массового тока; 
– плотность массы типичной частицы вещества в сопутствующей
частице системе отсчёта; 
– тензор энергии-импульса электромагнитного поля, 
– тензор энергии-импульса массовой компоненты общего поля.
Тензор выражается через сумму тензоров всех векторных
полей, действующих в системе, кроме тензора электромагнитного поля . Если обозначить 
как тензор
гравитационного поля, 
как тензор поля
ускорений, 
как тензор поля
давления, то можно записать:
.
В уравнении движения вещества (1) все тензоры берутся в
объёме, занятом веществом.
За
пределами вещества 4-токи 
и 
обнуляются, и как
следствие обнуляется левая часть (1). Но электромагнитное и гравитационное поля
существуют и за пределами заряженного вещества, и здесь не равны нулю ни
тензоры и , ни тензор , ни тензор энергии-импульса гравитационного поля 
. Кроме этого, становятся справедливы равенства 
, 
, и тогда (1) можно записать так [26]:
.
(2)
Если в (1) и (2) взять индекс 
, то получаются соотношения, описывающие обобщённую теорему
Пойнтинга.
Тензорное выражение (2) представляет собой
зависимость между плотностями энергии, плотностями потоков энергии и
натяжениями полей в каждой точке пространства вне вещества, и является
уравнением движения, записанным для электромагнитного и
гравитационного полей без учёта вещества. Подобные равенства с участием дивергенции
известны и для 4-векторов, например, уравнения непрерывности для 4-токов вида 
, 
. С математической точки зрения, равенство нулю дивергенции
4-вектора или тензора является соответствующим калибровочным условием, задающим
определённые связи между компонентами этого 4-вектора или тензора. Так,
калибровка электромагнитного поля по Лоренцу подразумевает, что для
электромагнитного 4-потенциала 
выполняется
соотношение 
.
Тензоры энергии-импульса , и в (1) и в (2)
выражаются соответственно через тензоры полей , и , и в записи с
контравариантными индексами имеют следующий вид:
,
,
,
где 
– электрическая постоянная, 
– скорость света, 
– метрический тензор, 
– коэффициент массовой компоненты общего
поля, 
– гравитационная постоянная.
В свою очередь, тензоры полей , и определяются из
соответствующих уравнений поля, выводимых из принципа наименьшего действия:
,
.
(3)
,
. (4)
, 
.
(5)
Здесь 
– символ Леви-Чивиты.
В [26] было найдено, что
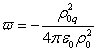. (6)
При выводе (6) использовалось условие
,
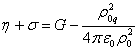(7)
где 
– коэффициент поля
ускорений, 
– коэффициент поля давления.
Условие (7) подразумевает, что рассматривается релятивистская однородная система, в которой кроме гравитационного и электромагнитного полей учитываются ещё поле ускорений и поле давления. Соотношение между коэффициентами полей в (7) является следствием баланса сил в уравнении движения [27] и баланса энергий в обобщённой теореме Пойнтинга [26], и было использовано в [28] в формулировке теоремы вириала.
Уравнения (3) и (5) решались в [29-30] для однородной релятивистской системы. При этом было обнаружено подобие выражений для тензоров полей:
.
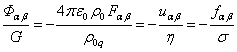(8)
Соотношение (8) было использовано для вывода (6) наряду с (7).
Компонентами тензора 
являются напряжённость
гравитационного поля,
делённая на скорость света, и поле кручения 
. Аналогично, компонентами тензора 
являются напряжённость
электрического поля,
делённая на скорость света, и магнитное поле 
. В неподвижной в целом однородной релятивистской системе
векторы и 
обнуляются, и тогда
можно считать, что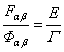 
. Предположим теперь, что мы моделируем протон с помощью
однородной релятивистской системы. Тогда плотность электрической силы,
действующей в веществе протона, будет равна 
, а плотность гравитационной силы составит 
. С учётом (8) для отношения модулей плотностей сил можно
записать:
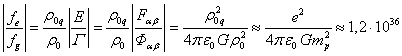. (9)
Здесь 
– элементарный заряд,
– масса протона.
Согласно (9), электрическое взаимодействие в протоне превышает гравитационное
взаимодействие приблизительно в 
раз. То же самое
получится, если разделить константу электромагнитного взаимодействия
(постоянную тонкой структуры) 
на константу
гравитационного взаимодействия 
. Отношение 
задаёт отношение энергии электрического взаимодействия двух
протонов к модулю энергии их гравитационного взаимодействия, без учёта энергий,
связанных с полями кручения и с магнитными полями. Представленный пример
показывает, что (8) справедливо даже в применении к протону.
Если подставить (6) в
(4), и учесть, что 
, 
, то получится следующее:
,
.
(10)
Из уравнений для 
в (10) и для 
в (3) следует, что
основным источником для тензоров массовой и зарядовой компонент общего поля
является зарядовый 4-ток 
. В [25] массовая и зарядовая компоненты общего поля были
связаны с соответствующими компонентами силового вакуумного поля таким образом,
что вакуумное поле порождает общее поле на макроскопическом уровне путём
действия на соответствующие 4-токи вещества. Мы можем ещё учесть результаты,
полученные в [5-6] в отношении компонент вакуумного поля. Отсюда следует следующая
гипотеза:
В рамках
модернизированной модели Фатио-Лесажа, силовое
вакуумное поле имеет две компоненты – поле гравитонов и поле заряженных частиц.
Среди этих заряженных частиц можно выделить праоны, которые идентифицируются как основные объекты
нижележащего уровня материи, из которых строятся все элементарные частицы.
Аналогично, звёзды, планеты и обычное вещество звёздного уровня материи состоят
из нуклонов, которые являются основными объектами нуклонного уровня материи.
Потоки заряженных праонов могут быть аналогичны по своим свойствам космическим
лучам высокой энергии, эти потоки возникают вблизи нуклонов и при
взаимодействии с заряженным 4-током 
вещества приводят к
электромагнитному взаимодействию. В качестве частиц поля гравитонов, порождающего
обычную гравитацию, предполагаются фотоны, нейтрино и праоны. Поскольку в (10)
мы связали между собой тензор массовой компоненты общего поля 
и зарядовый 4-ток 
, то логично считать, что основной компонентой вакуумного поля
являются потоки заряженных праонов. Эти потоки в нейтральном веществе создают
гравитационные силы, а также взаимодействия всех тех полей (поля ускорений,
поля давления, поля диссипации и т.д.), в уравнениях которых источником
является массовый 4-ток 
. Если же в веществе имеются некомпенсированные заряды, то
потоки заряженных праонов порождают ещё электромагнитное взаимодействие этих
зарядов друг с другом.
3. Дополнительные замечания
Анализ зависимости
электромагнитного и гравитационного взаимодействий от потоков заряженных частиц
вакуумного поля показывает, что эта зависимость не является линейной. Это видно
из того, что при переходе между уровнями материи электрическая постоянная 
не меняется, тогда как
при переходе с макроскопического уровня звёзд на уровень нуклонов
гравитационная постоянная 
должна быть заменена
на постоянную сильной гравитации 
, как указывается в [31-32]. В то же время согласно [6] сечение
взаимодействия гравитонов с веществом, приводящее к сильной гравитации,
совпадает с сечением взаимодействия праонов с веществом, приводящим к электромагнитному
взаимодействию, и приблизительно равно сечению протона. Равенство сечений
взаимодействий обосновывает то, что и за сильную гравитацию и за
электромагнитные явления на уровне нуклонов ответственны заряженные частицы,
которые могут отличаться друг от друга и иметь разное происхождение.
В частности, нижележащим по отношению к праонам уровнем материи является уровень граонов, и по индукции предполагается, что праоны состоят из граонов так же, как нейтронные звёзды состоят из нуклонов, а нуклоны состоят из праонов. При этом потоки заряженных граонов действуют подобно потокам заряженных праонов и являются отдельной компонентой вакуумного поля, порождающей сильную гравитацию.
Из вышеизложенного следует первичность электромагнитного поля по сравнению с гравитационным полем в том смысле, что потоки заряженных частиц на разных уровнях материи образуют многокомпонентное вакуумное поле и являются источником электромагнитного и гравитационного взаимодействий. В свою очередь, первичность гравитационного поля по сравнению с электромагнитным полем видна в том, что именно гравитация образует основные объекты на уровнях материи, такие как нейтронные звёзды, нуклоны, праоны, граоны и т.д. Каждый основной объект обладает сильными электрическими, магнитными и гравитационными полями, построен из основных объектов нижележащих уровней материи, и при взаимодействии с ними порождает потоки заряженных частиц. Эти потоки частиц от множества основных объектов складываются вместе и порождают силовое вакуумное поле, заполняющее всё пространство и придающее телам инерцию и массу [5].
Электромагнитные волны рассматриваются обычно как потоки фотонов, что лучше всего подтверждается явлением фотоэффекта. Субстанциональная модель фотона предполагает, что фотон образуется возбуждённым атомом за счёт действия полей ядра и электронов на заряженные частицы вакуумного поля (праоны), пересекающие атомный объём [33]. При этом за целостность возникающего фотона ответственна сильная гравитация, удерживающая праоны вместе, аналогично действию сильной гравитации на нуклоны в атомных ядрах. В результате и фотоны и атомные ядра оказываются весьма стабильными объектами.
Физический механизм действия потоков мельчайших заряженных частиц вакуума в веществе описан в [6]. Заряженные частицы имеют и заряд и массу, и потому взаимодействуют с электрическими и магнитными полями, а также с полями сильной гравитации и полями кручения (гравитомагнитными полями) ядер атомов и электронов вещества. Такое взаимодействие описывается силой Лоренца, которая не существенно изменяет амплитуду скорости частиц, но меняет направление движения этих частиц. В результате частицы изменяют направление своих импульсов, приводя к возникновению электромагнитных и гравитационных сил в веществе. Так как частицы почти не теряют свой энергии при движении в веществе, заметного нагрева тел не происходит.
Увеличение тепловой энергии в веществе сопровождается увеличением факторов Лоренца движения атомов, нуклонов и электронов, при этом все поля в веществе пропорциональны данным факторам Лоренца. Это приводит к усилению взаимодействия заряженных частиц вакуума с веществом, к увеличению энергии и инертной массы системы. На основе представленного механизма модель Лесажа объясняет вклад любого вида энергии в гравитационные и электромагнитные явления.
С другой стороны, в равновесной релятивистской однородной системе температура в центре всегда превышает температуру вещества в других точках системы. В равновесии при заданных размерах системы с учётом излучения тепловой энергии во внешнее пространство, сохраняется определённое распределение температуры внутри системы. Поскольку движение вещества системы и действующие силы в этом веществе являются следствием действия потоков заряженных частиц вакуума, то можно считать, что кинетическая энергия и некоторый нагрев вещества происходят от потери энергии потоков заряженных частиц в веществе.
Чем более плотное
вещество, тем более оно нагревается. Так, оценка температуры в центре
нейтронной звезды, найденная с помощью теории
поля через фактор Лоренца 
, даёт значение 
К [7].
Другим способом
средняя температура 
вещества звезды может
быть оценена с помощью теоремы вириала [28]. Для большего удобства, в [34]
кинетическая энергия 
движения типичных
частиц системы была связана не только со всей потенциальной энергией системы,
как в обычной теореме вириала, но и с энергией гравитационного и
электромагнитного полей за пределами системы, которая легко вычисляется:
.
Здесь 
и 
обозначают суммарную
инвариантную массу и суммарный заряд всех типичных частиц системы,
соответственно; 
есть радиус системы.
Мы можем считать, что
, 
,
где 
– постоянная
Больцмана, 
– количество типичных
частиц, 
– масса типичной
частицы.
Отсюда для случая 
имеем:
.
В незаряженной
нейтронной звезде ; 
практически равно
массе типичной звезды 
, где 
есть масса Солнца; 
можно взять равным
массе протона; 
равно радиусу звезды
12 км; 
. В результате получается усреднённая по объёму температура 
К. Таким образом, если
радиус звезды не меняется, теорема вириала гарантирует некоторую неизменную
температуру вещества звезды. На
наш взгляд это возможно, когда охлаждающаяся звезда после своего образования
потеряет путём излучения часть своей первоначальной энергии, полученной при
взрыве сверхновой. В какой-то момент потеря энергии за счёт излучения станет
равной притоку энергии от потоков заряженных частиц вакуума, падающих на
звезду, и наступит равновесное состояние.
4. Заключение
Из уравнений векторных
полей, действующих в рассматриваемой физической системе, мы выводим, что не
только тензор электромагнитного поля 
, но и тензор 
имеют в качестве
своего источника зарядовый 4-ток 
. Заметим ещё, что основной вклад в делает тензор
гравитационного поля 
. Тензоры и представляют собой
тензор зарядовой компоненты общего поля и тензор массовой компоненты общего
поля, соответственно. В [25] предполагалось, что зарядовая
компонента общего поля проявляется в связи с зарядовой компонентой
вакуумного поля, а массовая компонента общего поля связана с массовой
компонентой вакуумного поля. Но зависимость 
и 
от 
указывает на то, что
зарядовая компонента вакуумного поля в виде потоков заряженных частиц типа
праонов может играть центральную роль в возникновении электромагнитных и
гравитационных эффектов, в действии полей ускорений и давления в веществе, а
также и в проявлении действия других векторных полей.
По определению в [20] поле диссипации рассматривается как векторное поле и описывает дополнительные силы, появляющиеся в веществе в процессах трения. Эти силы переводят также энергию из кинетической формы в потенциальную форму и наоборот. Как векторные могут рассматриваться и поля слабого и сильного взаимодействий, так что им можно приписать свои тензоры и тензоры энергии-импульса [21]. Данные поля наиболее важны для расчётов в недрах звёзд, где активно протекают реакции с участием слабого и сильного взаимодействий. Поскольку каждое движение в веществе мы сводим к действию потоков заряженных частиц многокомпонентного электрогравитационного вакуума, то логично предположить, что и поле диссипации, и макроскопические поля слабого и сильного взаимодействий также обязаны своим происхождением зарядовой компоненте силового вакуумного поля.
Список использованных источников
2.
Le Sage G.L. Letter à une académicien de
Dijon.., Mercure de France, pp. 153-171 (1756).
3.
Le Sage G.L. Essai de Chymie Mécanique. pp.121 (1761).
4.
Le Sage G.L. Physique Mécanique. In: Prévost, P. Deux
traités de physique mécanique, publiés par Pierre Prévost, comme simple éditeur
du premier et comme auteur du second. J.J. Paschoud, Genève, Switzerland (1818).
5.
Fedosin S.G. The graviton field as the source of mass and gravitational force in the
modernized Le Sage’s model.
Physical
Science International Journal, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197; Поле гравитонов как источник
гравитационной силы и массы в модернизированной модели Лесажа.
6.
Fedosin S.G. The charged component of the vacuum field as the source of electric
force in the modernized Le Sage’s model. Journal of Fundamental and Applied
Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). doi:10.4314/jfas.v8i3.18; Заряженная компонента вакуумного поля как источник электрической силы в модернизированной модели Лесажа.
7.
Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within
the Framework of the Covariant Theory of Gravitation. International Letters of
Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39; Гравитационное поле в релятивистской однородной модели в рамках ковариантной теории гравитации.
8.
Heaviside O. A
gravitational and electromagnetic analogy. The Electrician, Vol. 31 (Part I),
pp. 281-282 and 359 (1893).
9.
Jefimenko O.D. 2006.
Gravitation and cogravitation. Developing Newton's theory of gravitation to its
physical and mathematical conclusion. Electret Scientific Publishing,
Star City, USA. pp.
367.
10.
Zakharenko A.A. On
piezogravitocogravitoelectromagnetic shear-horizontal acoustic waves. Canadian
Journal of Pure and Applied Sciences, Vol. 10 (3), pp. 4011-4028 (2016). https://doi.org/10.5281/zenodo.1301184.
11.
Borodikhin V.N. Vector theory of gravity. Gravit. Cosmol. Vol. 17, pp. 161-165
(2011). https://doi.org/10.1134/S0202289311020071.
12.
Flanders W.D., Japaridze G.S. Photon deflection and precession of the
periastron in terms of spatial gravitational fields. Class. Quant. Gravit. Vol. 21, pp. 1825-1831
(2004). https://doi.org/10.1088/0264-9381/21/7/007.
13.
Nyambuya G.G. Fundamental
Physical Basis for Maxwell-Heaviside Gravitomagnetism. Journal of Modern
Physics, Vol. 6, pp. 1207-1219 (2015). http://dx.doi.org/10.4236/jmp.2015.69125.
14.
Behera H. Comments on gravitoelectromagnetism of Ummarino and Gallerati
in “Superconductor in a weak static gravitational field” vs other versions.
Eur. Phys. J. C. Vol. 77, Article number 822 (2017). https://doi.org/10.1140/epjc/s10052-017-5386-4.
15.
Ummarino G.A., Gallerati
A. Superconductor in a weak static gravitational field. Eur. Phys. J. C. Vol.
77, Article number 549 (2017). https://doi.org/10.1140/epjc/s10052-017-5116-y.
16.
Ruggiero M.L., Tartaglia
A. Gravitomagnetic effects. II Nuovo Cimento B, Vol. 117, Issue 07, pp. 743-768
(2002).
17.
Mashhoon B. On the gravitational analogue of Larmor’s theorem. Phys.
Lett. A, Vol. 173,
pp. 347-354 (1993).
18.
Clark S.J., Tucker R.W. Gauge symmetry and gravito-electromagnetism.
Classical and Quantum Gravity. Vol.
17 (19), pp. 4125-4157 (2000). doi:10.1088/0264-9381/17/19/311.
19. Fedosin S.G. The Principle of Least
Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35,
No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804; Принцип наименьшего действия в ковариантной
теории гравитации.
20.
Fedosin
S.G. Four-Dimensional Equation of Motion for Viscous
Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure
Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18 (No. 1), pp. 13-24
(2015). doi:10.5541/ijot.5000034003; Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.
21. Fedosin
S.G. The Concept of
the General Force Vector Field. OALib Journal,
Vol. 3, pp. 1-15
(2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; Концепция
общего силового векторного поля.
22.
Shawyer R. Second
generation EmDrive propulsion applied to SSTO launcher and interstellar probe.
Acta Astronautica, Vol. 116, pp. 166-174 (2015). http://dx.doi.org/10.1016/j.actaastro.2015.07.002.
23.
White H., March O.,
Lawrence J., Vera J., Sylvester A. Measurement of Impulsive Thrust from a
Closed Radio-Frequency Cavity in Vacuum. Journal of Propulsion and Power, Vol.
33, no. 4, pp. 830-841 (2017). https://doi.org/10.2514/1.B36120.
24.
Леонов В.С., Бакланов О.Д., Саутин М.В., Костин Г.В.,
Кубасов А.А., Алтунин С.Е., Кулаковский О.М. Неракетный нереактивный квантовый
двигатель: идея, технология, результаты, перспективы. Воздушно-космическая сфера, No 1 (98). С. 68-75 (2019). http://dx.doi.org/10.30981/2587-7992-2019-98-1-68-75;
Leonov V.S., Baklanov O.D., Sautin M.V., Kostin G.V., Kubasov A.A., Altunin
S.Y., Kulakovsky O.M. Non-rocket non-reactive quantum engine: idea, technology,
results, prospects. Aerospace Sphere Journal, No 1 (98). pp. 68-75 (2019).
25. Fedosin
S.G. Two components of the macroscopic general field. Reports in Advances of
Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages
(2017). http://dx.doi.org/10.1142/S2424942417500025; Две компоненты макроскопического общего поля.
26. Fedosin S.G. The generalized
Poynting theorem for the general field and solution of the 4/3 problem.
International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19; Обобщённая
теорема Пойнтинга для
общего поля и
решение проблемы 4/3.
27.
Fedosin S.G. Estimation of the physical parameters of planets and stars
in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка
физических параметров планет и звёзд в модели гравитационного равновесия.
28.
Fedosin S.G. The virial theorem and the kinetic
energy of particles of a macroscopic system in the general field concept. Continuum
Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371
(2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и
кинетическая энергия частиц макроскопической системы в
концепции общего поля.
29. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics, Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого поля.
30. Fedosin
S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based
on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi:10.11648/j.ajmp.20140304.12; Интегральный
4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля
ускорений.
31. Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
32. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35,
No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451; Радиус протона в самосогласованной модели.
33. Fedosin S.G. The substantial model
of the photon. Journal of Fundamental and Applied Sciences, Vol. 9, No. 1, pp.
411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.
// Субстанциональная модель фотона.
34. Fedosin S.G. The binding energy and
the total energy of a macroscopic body in the relativistic uniform model. Middle
East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06; Энергия связи и полная энергия макроскопического
тела в релятивистской однородной модели.
Источник: http://sergf.ru/oc.htm