Acceleration tensor

The acceleration tensor is an antisymmetric tensor describing the four-acceleration of particles and consisting of six components. Tensor components are at the same time components of the two three-dimensional vectors – acceleration field strength and the solenoidal acceleration vector. With the acceleration tensor the acceleration stress-energy tensor, the acceleration field equations and the four-force density in matter are defined. Acceleration field in matter is a component of general field.

1 Definition
2 Expression for the components
3 Properties of tensor
4 Acceleration field
5 Covariant theory of gravitation

5.1 Acceleration stress-energy tensor
5.2 Action and Lagrangian
5.3 Generalized velocity and Hamiltonian

6 Special theory of relativity
7 Other theories
8 See also
9 References
10 External links

Definition

Expression for the acceleration tensor can be found in papers by Sergey Fedosin, ^[1] ^[2] where the tensor is defined using 4-curl:

$u_{\mu \nu} = \nabla_\mu U_\nu - \nabla_\nu U_\mu = \frac{\partial U_\nu}{\partial x^\mu} - \frac{\partial U_\mu}{\partial x^\nu}.\qquad\qquad (1)$

Here the acceleration 4-potential $~ U_\mu$ is given by:

$~ U_\mu = \left( \frac {\vartheta }{ c}, -\mathbf{U } \right),$

where $~\vartheta$ is the scalar potential, $~ \mathbf{U }$ is the vector potential of acceleration field, – speed of light.

Expression for the components

The acceleration field strength and the solenoidal acceleration vector are found with the help of (1):

$~ S_i= c (\partial_0 U_i -\partial_i U_0),$

$~ N_k= \partial_i U_j -\partial_j U_i ,$

and in the second expression three numbers are composed of non-recurring sets 1,2,3; or 2,1,3; or 3,2,1 etc.

In vector notation can be written:

$~\mathbf{S}= -\nabla \vartheta - \frac{\partial \mathbf{U }} {\partial t},$

$~\mathbf{N }= \nabla \times \mathbf{U }.$

The acceleration tensor consists of the components of these vectors:

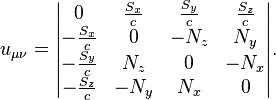
$~ u_{\mu \nu}= \begin{vmatrix} 0 & \frac {S_x}{ c} & \frac {S_y}{ c} & \frac {S_z}{ c} \\ -\frac {S_x}{ c} & 0 & - N_{z} & N_{y} \\ -\frac {S_y}{ c} & N_{z} & 0 & -N_{x} \\ -\frac {S_z}{ c}& -N_{y} & N_{x} & 0 \end{vmatrix}.$

The transition to the acceleration tensor with contravariant indices is carried out by multiplying by double metric tensor:

$~ u^{\alpha \beta}= g^{\alpha \nu} g^{\mu \beta} u_{\mu \nu}.$

In the special relativity, this tensor has the form:

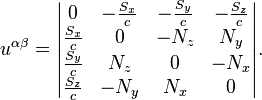
$~ u^{\alpha \beta}= \begin{vmatrix} 0 &- \frac {S_{x}}{ c} & -\frac {S_{y}}{ c} & -\frac {S_{z}}{ c} \\ \frac {S_{x}}{ c} & 0 & - N_{z} & N_{y} \\ \frac {S_{y}}{ c}& N_{z} & 0 & -N_{x} \\ \frac {S_{z}}{ c}& -N_{y} & N_{x} & 0 \end{vmatrix}.$

For the vectors, related to the specific point particle, considered as a solid body, we can write:

$~\mathbf{S}= - c^2 \nabla \gamma - \frac{\partial (\gamma \mathbf{v })} {\partial t},$

$~\mathbf{N }= \nabla \times (\gamma \mathbf{v }),$

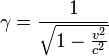where $~\gamma = \frac {1}{\sqrt{1 - {v^2 \over c^2}}}$ , $~\mathbf{v }$ is the velocity of the particle.

To transform the components of the acceleration tensor from one inertial system to another we must take into account the transformation rule for tensors. If the reference frame K' moves with an arbitrary constant velocity $~ \mathbf {V}$ with respect to the fixed reference system K, and the axes of the coordinate systems parallel to each other, the acceleration field strength and the solenoidal acceleration vector are transformed as follows:

$\mathbf {S}^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {S}) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {S}-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {S}) + [\mathbf {V} \times \mathbf {N }] \right),$

$\mathbf {N }^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {N }) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {N }-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {N }) - \frac {1}{ c^2} [\mathbf {V} \times \mathbf {S}] \right).$

Properties of tensor

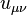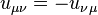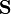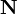$~ u_{\mu \nu}$ is the antisymmetric tensor of rank 2, it follows from this condition $~ u_{\mu \nu}= -u_{\nu \mu}$ . Three of the six independent components of the acceleration tensor associated with the components of the acceleration field strength $~\mathbf{ S }$ , and the other three – with the components of the solenoidal acceleration vector $~\mathbf{N }$ . 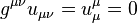Due to the antisymmetry such invariant as the contraction of the tensor with the metric tensor vanishes: $~ g^{\mu \nu} u_{\mu \nu}= u^{\mu}_\mu =0$ .
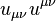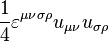Contraction of tensor with itself $u_{\mu \nu} u^{\mu \nu}$ is an invariant, and the contraction of tensor product with Levi-Civita symbol as $\frac {1}{4} \varepsilon^{\mu \nu \sigma \rho} u_{\mu \nu} u_{\sigma \rho}$ is the pseudoscalar invariant. These invariants in the special relativity can be expressed as follows:

$u_{\mu \nu} u^{\mu \nu} = -\frac {2}{c^2} (S^2- c^2 N^2) = inv,$

$\frac {1}{4} \varepsilon^{\mu \nu \sigma \rho}u_{\mu \nu} u_{\sigma \rho} = - \frac {2}{ c } \left( \mathbf S \cdot \mathbf {N} \right) = inv.$

Determinant of the tensor is also Lorentz invariant:

$\det \left( u_{\mu \nu} \right) = \frac{4}{c^2} \left(\mathbf S \cdot \mathbf {N} \right)^{2}.$

Acceleration field

Through the acceleration tensor the equations of acceleration field are written:

$\nabla_\sigma u_{\mu \nu}+\nabla_\mu u_{\nu \sigma}+\nabla_\nu u_{\sigma \mu}=\frac{\partial u_{\mu \nu}}{\partial x^\sigma} + \frac{\partial u_{\nu \sigma}}{\partial x^\mu} + \frac{\partial u_{\sigma \mu}}{\partial x^\nu} = 0. \qquad\qquad (2)$

$~ \nabla_\nu u^{\mu \nu} = - \frac{4 \pi \eta }{c^2} J^\mu, \qquad\qquad (3)$

where $J^\mu = \rho_{0} u^\mu$ is the mass 4-current, $\rho_{0}$ is the mass density in comoving reference frame, $u^\mu$ is the 4-velocity, $~ \eta$ is a constant of acceleration field.

Instead of (2) it is possible use the expression:

$~ \varepsilon^{\mu \nu \sigma \rho}\frac{\partial u_{\mu \nu}}{\partial x^\sigma} = 0 .$

Equation (2) is satisfied identically, which is proved by substituting into it the definition for the acceleration tensor according to (1). If in (2) we insert tensor components $u_{\mu \nu}$ , this leads to two vector equations:

$~ \nabla \times \mathbf{S} = - \frac{\partial \mathbf{N} } {\partial t} , \qquad\qquad (4)$

$~ \nabla \cdot \mathbf{N} = 0 . \qquad\qquad (5)$

According to (5), the solenoidal acceleration vector has no sources as its divergence vanishes. From (4) follows that the time variation of the solenoidal acceleration vector leads to a curl of the acceleration field strength.

Equation (3) relates the acceleration field to its source in the form of mass 4-current. In Minkowski space of special relativity the form of the equation is simplified and becomes:

$~ \nabla \cdot \mathbf{S} = 4 \pi \eta \rho,$

$~ \nabla \times \mathbf{N} = \frac{1}{c^2} \left( 4 \pi \eta \mathbf{J} + \frac{\partial \mathbf{S}} {\partial t} \right),$

where $~ \rho$ is the density of moving mass, $~ \mathbf{J}$ is the density of mass current.

According to the first of these equations, the acceleration field strength is generated by the mass density, and according to the second equation the mass current or change in time of the acceleration field strength generate the circular field of the solenoidal acceleration vector.

From (3) and (1) it can be obtained:^[1]

$~ R_{ \mu \alpha } u^{\mu \alpha }= \frac {4 \pi \eta }{c^2} \nabla_{\alpha}J^{\alpha}.$

The continuity equation for the mass 4-current $~\nabla _{{\alpha }}J^{{\alpha }}=0$ is a gauge condition that is used to derive the field equation (3) from the principle of least action. On the other hand, the contraction of the acceleration tensor and the Ricci tensor is equal to zero,

$~R_{{\mu \alpha }}u^{{\mu \alpha }}=0,$ as a consequence of the antisymmetry of the acceleration tensor.

In Minkowski space the covariant derivative becomes the partial derivative, and the continuity equation becomes as follows:

$~\partial _{{\alpha }}J^{\alpha }={\frac {\partial \rho }{\partial t}}+\nabla \cdot {\mathbf {J}}=0.$

The wave equation for the acceleration tensor is written as: ^[3]

$~\nabla ^{\sigma }\nabla _{\sigma }u_{{\mu \nu }}={\frac {4\pi \eta }{c^{2}}}\nabla _{\mu }J_{\nu }-{\frac {4\pi \eta }{c^{2}}}\nabla _{\nu }J_{\mu }+u_{{\nu \rho }}{R^{\rho }}_{\mu }-u_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}u^{{\eta \lambda }}.$

This equation is valid provided that the Ricci tensor is defined as a result of contraction of metric tensor and curvature tensor in the form ^[4]

$~R_{{\mu \nu }}=g^{{\alpha \beta }}R_{{\mu \alpha \beta \nu }}.$

If the Ricci tensor is defined as ^[5]

$~R_{{\alpha \nu }}=g^{{\mu \beta }}R_{{\mu \alpha \beta \nu }},$

then the wave equation for the acceleration tensor will be:

$~\nabla ^{\sigma }\nabla _{\sigma }u_{{\mu \nu }}={\frac {4\pi \eta }{c^{2}}}\nabla _{\mu }J_{\nu }-{\frac {4\pi \eta }{c^{2}}}\nabla _{\nu }J_{\mu }-u_{{\nu \rho }}{R^{\rho }}_{\mu }+u_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}u^{{\eta \lambda }}.$

Covariant theory of gravitation

Acceleration stress-energy tensor

With the help of acceleration tensor in the covariant theory of gravitation the acceleration stress-energy tensor is constructed:

$~ B^{ik} = \frac{c^2} {4 \pi \eta }\left( -g^{im} u_{n m} u^{n k}+ \frac{1} {4} g^{ik} u_{m r} u^{m r}\right)$ .

The covariant derivative of the acceleration stress-energy tensor with mixed indices determines the four-force density: ^[3]

$~ f_\alpha = \nabla_\beta {B_\alpha}^\beta = - u_{\alpha k} J^k = - \rho_0 u_{\alpha k}u^k = \rho_0 \frac {DU_\alpha }{D \tau}- J^k \nabla_\alpha U_k = \rho_0 \frac {dU_\alpha }{d \tau} - J^k \partial_\alpha U_k ,\qquad \qquad (6)$

here the operator of proper-time-derivative with respect to proper time $~ \tau$ is used.

The density of the 4-force can be written for the time and space component in the form of two expressions:

$~ f_0 = \nabla_\beta {B_0}^\beta = - u_{0 k} J^k = - \rho_0 \frac {dt}{ ds } (\mathbf{S }\cdot \mathbf{v }) ,$

$~ f_i = \nabla_\beta {B_i}^\beta = - u_{i k} J^k = c \rho_0 \frac {dt}{ ds } (\mathbf{S }+ [\mathbf {v} \times \mathbf {N}] ),$

where denotes a four-dimensional space-time interval,

Action and Lagrangian

Total Lagrangian for the matter in gravitational and electromagnetic fields includes the acceleration tensor and is contained in the action function: ^[1]

$~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}D_\mu J^\mu + \frac {c}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu} -\frac {1}{c}A_\mu j^\mu - \frac {c \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu} -$

$~ -\frac {1}{c}U_\mu J^\mu - \frac {c }{16 \pi \eta } u_{ \mu\nu} u^{ \mu\nu} -\frac {1}{c} \pi_\mu J^\mu - \frac {c }{16 \pi \sigma } f_{ \mu\nu}f^{ \mu\nu} ) \sqrt {-g}d\Sigma,$

where is Lagrangian, is differential of coordinate time, is a certain coefficient, is the scalar curvature, $~\Lambda$ is the cosmological constant, which is a function of the system, is the speed of light as a measure of the propagation speed of electromagnetic and gravitational interactions, $~ D_\mu$ is the gravitational four-potential, is the gravitational constant, $~ \Phi_{ \mu\nu}$ is the gravitational tensor, $~ A_\mu$ is the electromagnetic 4-potential, $~ j^\mu$ is the electromagnetic 4-current, $~\varepsilon_0$ is the electric constant, $~ F_{ \mu\nu }$ is the electromagnetic tensor, $~ U_\mu$ is the 4-potential of acceleration field, $~ \eta$ and $~ \sigma$ are the constants of acceleration field and pressure field, respectively, $~ u_{ \mu\nu}$ is the acceleration tensor, $~ \pi_\mu$ is the 4-potential of pressure field, $~ f_{ \mu\nu}$ is pressure field tensor, $~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3$ is the invariant 4-volume, $~\sqrt {-g}$ is the square root of the determinant of metric tensor, taken with a negative sign, is the product of differentials of the spatial coordinates.

The variation of the action function by 4-coordinates leads to the equation of motion of the matter unit in gravitational and electromagnetic fields and pressure field:

$~ -u_{\beta \sigma} \rho_{0} u^\sigma = \rho_0 \frac{ dU_\beta } {d \tau }- \rho_0 u^\sigma \partial_\beta U_\sigma = \Phi_{\beta \sigma} \rho_0 u^\sigma + F_{\beta \sigma} \rho_{0q} u^\sigma + f_{\beta \sigma} \rho_0 u^\sigma ,$

where the first term on the right is the gravitational force density, expressed with the help of the gravitational field tensor, second term is the Lorentz electromagnetic force density for the charge density $~ \rho_{0q}$ measured in the comoving reference frame, and the last term sets the pressure force density.

If we vary the action function by the acceleration 4-potential, we obtain the equation of acceleration field (3).

Generalized velocity and Hamiltonian

The covariant 4-vector of generalized velocity, considered as 4-potential of [[general field]], is given by the expression:

$~ s_{\mu } = U_{\mu } +D_{\mu } + \frac {\rho_{0q} }{\rho_0 }A_{\mu }+ \pi_{\mu} .$

With regard to the generalized 4-velocity, the Hamiltonian contains the acceleration tensor and has the form:

$~H = \int {( s_0 J^0 - \frac {c^2}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu}+ \frac {c^2 \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu }+ \frac {c^2 }{16 \pi \eta } u_{ \mu\nu} u^{ \mu\nu}+ \frac {c^2 }{16 \pi \sigma } f_{ \mu\nu} f^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},$

Where and are the time components of the 4-vectors $~ s_{\mu }$ and $~ J^{\mu }$ .

In the reference frame that is fixed relative to the system's center-of-momentum frame, Hamiltonian will determine the invariant energy of the system.

The acceleration tensor is used to calculate the generalized 4-momentum,^[6] the energy, momentum, and 4-momentum of a physical system, ^[7] as well as the angular momentum pseudotensor. ^[2]

Special theory of relativity

Studying Lorentz covariance of 4-force, Friedman and Scarr found not full covariance expressions for 4-force in the form $~ F^\mu = \frac {d p^\mu }{d \tau } .$ ^[8]

This led them to conclude that the four-acceleration must be expressed with the help of some antisymmetric tensor $~ {A^\mu}_\nu$ :

$~c \frac { d u^\mu }{d \tau } = {A^\mu}_\nu u^\nu .$

Based on the analysis of different types of motion, they rated their required values of the components of the acceleration tensor, thereby giving this tensor indirect definition.

From comparison with (6) it follows that the tensor $~ {A^\mu}_\nu$ up to a sign and a constant factor coincides with the acceleration tensor $~ {u^\alpha}_k$ in case when rectilinear motion of a solid body without rotation is considered. Then indeed the four-potential of the acceleration field coincides with the four-velocity, $~ U_\mu = u_\mu$ . As a result, the quantity $~ - J^k \partial_\alpha U_k =- \rho_0 u^k \partial_\alpha u_k$ on the right-hand side of (6) vanishes, since the following relations hold true: , $~ 2 u^k \partial_\alpha u_k = \partial_\alpha (u^k u_k) = \partial_\alpha c^2 =0$ . With this in mind, in (6) we can raise the index $~ \alpha$ and cancel the mass density, which gives the following:

$~ - {u^\alpha}_k u^k =\frac {du^\alpha }{d \tau} .$

Mashhoon and Muench considered transformation of inertial reference systems, related to accelerated frame of reference, and came to the relation: ^[9]

$~c \frac { d \lambda_\alpha }{d \tau } = {\Phi_\alpha}^\beta \lambda_\beta.$

Tensor $~ {\Phi_\alpha}^\beta$ has the same properties as the acceleration tensor $~ {u_\alpha}^\beta.$

Other theories

In the articles ^{[10] [11]} ^[12]devoted to the modified Newtonian dynamics (MOND), in the tensor-vector-scalar gravity appear scalar function $~ \psi$ or $~ \phi$ , that defines a scalar field, and 4-vector $\mathfrak {U}_\mu$ or $A_\mu$ , and 4-tensor $\mathfrak {U}_{[\mu\nu ]}$ or $F_{ab} = \frac{\partial A_b}{\partial x^a} - \frac{\partial A_a}{\partial x^b}.$

The analysis of these values in the corresponding Lagrangian demonstrates that scalar function $~ \psi$ or $~ \phi$ correspond to scalar potential $~\vartheta$ of the acceleration field; 4-vector $\mathfrak {U}_\mu$ or $A_\mu$ correspond to 4-potential $~ U_\mu$ of the acceleration field; 4-tensor $\mathfrak {U}_{[\mu\nu ]}$ or $F_{ab}$ correspond to acceleration tensor $u_{\mu \nu}$ .

As it is known, the acceleration field is not intended to explain the accelerated motion, but for its accurate description. In this case, it can be assumed that the tensor-vector-scalar theories cannot pretend to explain the rotation curves of galaxies. At best, they can only serve to describe the motion, for example to describe the rotation of stars in galaxies and the rotation of galaxies in clusters of galaxies.

References

^1.0 ^{1.1 1.2} Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
²^.0 ²^.1Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X.
^3.0 ^.3.1Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
Fock V.A. The Theory of Space, Time and Gravitation (Pergamon Press, London, 1959).
Landau L.D., Lifshitz E.M. The Classical Theory of Fields, (1951). Pergamon Press. ISBN 7-5062-4256-7.
Fedosin S.G. Generalized Four-momentum for Continuously Distributed Materials. Gazi University Journal of Science, Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793.
Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.
Yaakov Friedman and Tzvi Scarr. Covariant Uniform Acceleration. Journal of Physics: Conference Series Vol. 437 (2013) 012009 doi:10.1088/1742-6596/437/1/012009.
Bahram Mashhoon and Uwe Muench. Length measurement in accelerated systems. Annalen der Physik. Vol. 11, Issue 7, P. 532–547, 2002.
J. D. Bekenstein and M. Milgrom, Does the Missing Mass Problem Signal the Breakdown of Newtonian Gravity ? Astrophys. Journ. 286, 7 (1984).
Bekenstein, J. D. (2004), Relativistic gravitation theory for the modified Newtonian dynamics paradigm, Physical Review D 70 (8): 083509, https://dx.doi.org/10.1103%2FPhysRevD.70.083509.
Exirifard, Q. (2013), GravitoMagnetic Field in Tensor-Vector-Scalar Theory, Journal of Cosmology and Astroparticle Physics, JCAP04: 034, https://dx.doi.org/10.1088%2F1475-7516%2F2013%2F04%2F034.

External links

Acceleration tensor in Russian

Source: http://sergf.ru/aten.htm

На русском языке