In English

Постоянная сильной гравитации

Материал из свободной русской энциклопедии «Традиция»

Постоянная сильной гравитации $~\;\; \Gamma$ — предполагаемая фундаментальная физическая постоянная, константа сильного гравитационного взаимодействия, действующего на уровне элементарных частиц.

Согласно ньютоновскому закону всемирного тяготения, сила гравитационного притяжения между двумя достаточно массивными материальными точками с гравитационными массами и , находящимися на расстоянии , равна:

$F= G \frac{m_1 m_2}{R^2}.$

Коэффициент пропорциональности в данном выражении называется гравитационная постоянная. В отличие от обычной силы гравитации, на уровне элементарных частиц действует сильная гравитация. Для её описания в формуле для гравитационной силы необходимо заменить на $~\Gamma$ :

$F_{sg}=\Gamma \frac{m_1 m_2}{R^2}.$

Идея сильной гравитации первоначально связывалась с математическим подходом Абдуса Салама при унификации гравитации и квантовой хромодинамики, а сейчас часто используется для обозначения любого исследования, предполагающего гравитацию на уровне частиц как основу сильного взаимодействия.

История появления

Имеется несколько способов оценки значения $~\Gamma$ . В предположении, что постоянная сильной гравитации зависит от типа объектов, из взаимодействия двух ядер дейтерия находится, ^[1] что $\Gamma =2{,}06 \cdot 10^{25}$ м³•с^–2•кг^–1.

На основе аналогии между адронами и чёрными дырами Керра — Ньюмена ^[2] Sivaram, C. и Sinha, K.P, ^[3] ^[4] Raut, Usha и Shina, KP ^[5] приняли значение $\Gamma =6{,}7 \cdot 10^{27}$ м³•с^–2•кг^–1.

Значение постоянной сильной гравитации позволяет оценить величину сильного спин-торсионного взаимодействия между вращающимися протонами. ^[6] Mongan написал статью, ^[7] в которой постоянная сильной гравитации равна $G_s = 1{,}1 \cdot 10^{28} \$ м³•с^–2•кг^–1. Согласно работам Олдершоу ^[8] значение постоянной сильной гравитации равно $\Gamma =2{,}18 \cdot 10^{28}$ м³•с^–2•кг^–1.

Как и у Олдершоу, постоянная сильной гравитации может быть связана ^[9] с радиусом протона , массой протона и скоростью света :

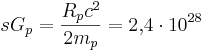$sG_p= \frac{R_p c^2}{2 m_p }= 2{,}4 \cdot 10^{28}$ м³•с^–2•кг^–1.

Согласно Tennakone, который рассматривал электрон и протон как чёрные дыры в сильном гравитационном поле, постоянная сильной гравитации равна: ^[10]

$\Gamma = 3{,}9 \cdot 10^{28}$ м³•с^–2•кг^–1.

Zane Andrea Quintili находит постоянную сильной гравитации на основе подобия между планковской массой и радиусом, и соответственно массой и радиусом протона: ^[11]

$G_{q}={\frac {8\hbar c}{m_{p}^{2}}}=9{,}04\cdot 10^{{28}}$ м³•с^–2•кг^–1.

Recami с соавторами ^[12] ^[13] определяют постоянную сильной гравитации через массу пиона $~m_{\pi}$ по формуле:

$N\approx \frac{h c}{ m^2_{\pi} }= 3{,}2 \cdot 10^{30}$ м³•с^–2•кг^–1,

где – постоянная Планка.

Отсюда они выводят константу сильного взаимодействия двух нуклонов в следующем виде: ^[14]

$\frac{ N g^2}{\hbar c } \approx 14$ , где обозначает сильный заряд, $~\hbar$ есть постоянная Дирака.

Станислав Фисенко с соавторами нашли ^[15] ^[16] спектр устойчивых состояний электрона в собственном гравитационном поле (0.511 MeV …0.681 MeV) с помощью постоянной сильной гравитации

$N= 5{,}1 \cdot 10^{31}$ м³•с^–2•кг^–1.

Авторы работы ^[17] при определении $~\Gamma$ отталкивались от постоянной Ферми, что привело их к значению $\Gamma =6{,}94 \cdot 10^{31}$ м³•с^–2•кг^–1.

В статье ^[18] можно найти значение постоянной сильной гравитации, равное $\Gamma =2{,}77 \cdot 10^{32}$ м³•с^–2•кг^–1.

В 1999 г. Сергей Федосин ввёл значение постоянной сильной гравитации на основе равенства между кулоновской электрической силой и силой гравитации в атоме водорода на радиусе Бора. В единицах СИ это приводит к следующему выражению для значения постоянной сильной гравитации: ^[19]

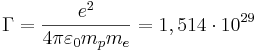$\Gamma= \frac{e^2}{4 \pi \varepsilon_{0} m_p m_e }=1,514 \cdot 10^{29}$ м³•с^–2•кг^–1,

где – элементарный заряд, $~\pi$ – число пи, $~\varepsilon_{0}$ – электрическая постоянная, – масса протона, – масса электрона.

При этом предполагается, что сильная гравитация, как универсальная сила, действует на вещество нуклонов, адронов, электронов и элементарных частиц независимо от типа этих частиц. В противоположность этому, в стандартном подходе считается, что сильное взаимодействие никак не действует на электроны и другие лептоны.

Малая масса и сильный заряд вещества не позволяют электрону целиком находиться в каком-то малом объёме вблизи ядра, и он приобретает дисковидную осесимметричную форму, ограниченную размером атома. В атоме водорода между ядром и веществом электрона действуют электрические силы притяжения, но они компенсируются силами расталкивания собственного заряда электрона. Остаются центростремительная сила от вращения электрона вокруг ядра, и гравитационное притяжение между массивным ядром и веществом электрона. Отсюда следует равенство действия всех сил, в том числе равенство действия сильной гравитации между массами ядра и электрона с одной стороны, и электрической силы между зарядами ядра и электрона, с другой стороны, позволяющее оценить значение $~\Gamma .$ Если $~R_{B}={\frac {\hbar }{m_{e}\alpha c}}$ есть радиус Бора, то равенство сил даёт:

${\frac {\Gamma m_{p}m_{e}}{R_{B}^{2}}}={\frac {e^{2}}{4\pi \varepsilon _{{0}}R_{B}^{2}}}.$

Постоянная тонкой структуры есть

$\alpha ={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}},$

Так что

$\Gamma ={\frac {\alpha \hbar c}{m_{p}m_{e}}},\qquad \qquad \hbar ={\frac {\Gamma m_{p}m_{e}}{\alpha c}}.$

Радиус Бора становится равным

$~R_{B}={\frac {\Gamma m_{p}}{\alpha ^{2}c^{2}}}={\frac {\Gamma m_{p}}{V_{B}^{2}}},$

где $~V_{B}=\alpha c$ есть орбитальная скорость электронного облака на первом уровне энергии.

Отсюда $~V_{B}^{2}={\frac {\Gamma m_{p}}{R_{B}}}$ , а кинетическая энергия электрона с учётом определения постоянной сильной гравитации равна:

$~K={\frac {m_{e}V_{B}^{2}}{2}}={\frac {\Gamma m_{p}m_{e}}{2R_{B}}}={\frac {e^{2}}{8\pi \varepsilon _{0}R_{B}}}=-{\frac {W}{2}},$

где есть потенциальная энергия электрона в электрическом поле ядра атома водорода.

Получается теорема вириала в виде $~K=-{\frac {W}{2}}$ . Находится также полная энергия электрона на первом уровне энергии:

$~E=K+W={\frac {W}{2}}=-K=-13,6$ эВ.

С помощью постоянной $~ \Gamma$ может быть записано равенство между энергией покоя протона и половиной потенциальной энергии поля сильной гравитации протона в виде шара согласно теореме вириала, ^[20] если считать, что для протона энергия связи $~E_{b}$ , с точностью до знака равная полной энергии, становится очень близкой к релятивистской энергии в виде энергии покоя:

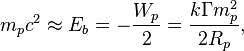
$~m_{p}c^{2}\approx E_{b}=-{\frac {W_{p}}{2}}={\frac {k\Gamma m_{p}^{2}}{2R_{p}}},$

где $~ R_p =8,73 \cdot 10^{-16}$ м есть радиус протона, (в гипотетическом случае однородной плотности вещества протона должно быть ). Отсюда следует, что масса нуклонов определяется энергией сильной гравитации в соответствии с принципом эквивалентности массы и энергии.

Если предположить, что магнитный момент протона создаётся за счёт максимального вращения положительного заряда, распределённого по объёму протона в виде шара, когда центростремительное ускорение на экваторе становится равным ускорению сильной гравитации, то формула для магнитного момента имеет вид:

$~P_m = \delta e \sqrt{\Gamma m_p R_p},$

где $~ P_m =1,41 \cdot 10^{-26}$ Дж/Тл есть магнитный момент протона, $~ \delta = 0,1875$ (в случае однородной плотности вещества и заряда протона должно быть $~ \delta = 0,2$ ).

Из формул для энергии и магнитного момента в самосогласованной модели определяется радиус протона. ^[21]

Постоянная сильной гравитации входит также в формулу, описывающую сильное взаимодействие с помощью сильной гравитации и поля кручения вращающихся частиц. ^[22] Особенностью эффекта гравитационной индукции является то, что если два тела вращаются вдоль одной оси и сближаются под действием силы гравитации, то эти тела будут увеличивать угловую скорость своего вращения. В связи с этим предполагается, что нуклоны в атомных ядрах вращаются с максимальной скоростью. Это может объяснить равновесие нуклонов в атомных ядрах как равновесие между силой притяжения от сильной гравитации и силой от поля кручения (от гравитомагнитной силы в гравитоэлектромагнетизме). В частности, константа взаимодействия равна:

$\alpha_{pp}= \frac{\beta \Gamma m^2_p }{\hbar c } =13{,}4 \beta$ ,

где $~ \beta$ равна 0,26 для взаимодействия двух нуклонов, и стремится к 1 для частиц с меньшей плотностью вещества.

Константа $~\alpha_{pp}$ близка к константе сильного взаимодействия двух нуклонов в Стандартной модели:

$\alpha_s= \frac{ g^2_{N \pi}}{4\pi\hbar c } \approx 14,6$ , где $~g_{N \pi}$ есть константа псевдоскалярного нуклон-пионного взаимодействия.

Постоянная тонкой структуры есть константа взаимодействия электромагнитного взаимодействия и может быть записана так:

$~ \alpha = \frac { \Gamma m_p m_e }{\hbar c }\approx \frac {1}{137,036}.$

Связь с обычной гравитационной константой

Если использовать подобие уровней материи и SPФ-симметрию, то значение $~\Gamma$ можно определить также через коэффициенты подобия и гравитационную постоянную обычной гравитации по формуле:

$\Gamma = G \frac{ \Phi }{ P S^2},$

где $~ \Phi =1,62 \cdot 10^{57}$ , $~ P= 1,4 \cdot 10^{19}$ , являются коэффициентами подобия по массе, размерам и скоростям соответственно, для вырожденных квантовых объектов на атомном и звёздном уровнях материи. ^[19] Степени коэффициентов подобия в данном равенстве соответствуют размерности гравитационной постоянной.

С точки зрения теории бесконечной вложенности материи и теории гравитации Лесажа, наличие двух гравитационных постоянных $~\Gamma$ и показывает различие свойств гравитонов и свойств вещества на разных уровнях материи. ^{[23] [24]}

В частности, для постоянной сильной гравитации и обычной гравитационной постоянной можно записать подобные друг другу соотношения, в которых эти постоянные выражаются через соответствующие плотности энергии потоков гравитонов электрогравитационного вакуума и параметры наиболее плотного объекта соответствующего уровня материи: ^[25]

$~\Gamma ={\frac {\varepsilon _{c}\vartheta ^{2}}{4\pi M_{n}^{2}}},\qquad \qquad G={\frac {\varepsilon _{{cs}}\vartheta _{s}^{2}}{4\pi M_{s}^{2}}},$

где $~\varepsilon _{c}=7,4\cdot 10^{{35}}$ Дж/м³ – плотность энергии потоков гравитонов для кубического распределения; $~\vartheta =2,67\cdot 10^{{-30}}$ м² – сечение взаимодействия заряженных частиц электрогравитационного вакуума (праонов) с нуклонами, которое очень близко по величине к геометрическому сечению нуклона и используется для вычисления электрической постоянной; $~M_{n}$ – масса нуклона; $\varepsilon _{{cs}}=\varepsilon _{c}{\frac {\Phi S^{2}}{P^{3}}}=2,3\cdot 10^{{34}}$ Дж/м³ – плотность энергии потоков гравитонов на уровне звёзд для кубического распределения; $~\vartheta _{s}=\vartheta P^{2}=5,2\cdot 10^{{8}}$ м² – сечение взаимодействия гравитонов с нейтронной звездой; $~M_{s}=M_{n}\Phi =2,7\cdot 10^{{30}}$ кг – масса нейтронной звезды.

На уровне материи праонов должна действовать своя собственная постоянная сильной гравитации $~G_{{pr}}$ . Считая, что коэффициент подобия по скоростям между нуклонным и праонным уровнями материи равен $~S\approx 1$ , можно записать:

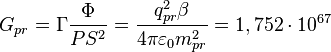$G_{{pr}}=\Gamma {\frac {\Phi }{PS^{2}}}={\frac {q_{{pr}}^{2}\beta }{4\pi \varepsilon _{{0}}m_{{pr}}^{2}}}=1,752\cdot 10^{{67}}$ м³•с^–2•кг^–1,

где $~q_{{pr}}=1,06\cdot 10^{{-57}}$ Кл есть заряд праона, $~m_{{pr}}=1\cdot 10^{{-84}}$ кг – масса праона,

$~\beta ={\frac {m_{p}}{m_{e}}}=1836,152$ – отношение массы протона к массе электрона.

Примечания

J. Dufour. “Very sizeable increase of gravity at pico-meter distance: a novel working hypothesis to explain anomalous heat effects and apparent transmutations in certain metal hydrogen systems”. J. of condensed matter nuclear science, Vol. 1, pp. 47-61 (2007). [1]
Strong Interactions, Gravitation and Cosmology. Abdus Salam Publ. in: NATO Advanced Study Institute, Erice, June16-July 6, 1972 ; in: High Energy Astrophysics and its Relation to Elementary Particle Physics, 441-452 MIT Press, Cambridge (1974).
Sivaram, C. and Sinha, K.P. Strong gravity, black holes, and hadrons. Physical Review D, Vol. 16, Issue 6, pp. 1975-1978 (1977).
Salam A. and Sivaram C. Strong Gravity Approach to QCD and Confinement. Mod. Phys. Lett., v. A8(4), pp. 321-326 (1993).
Raut, Usha and Shina, KP (1983) Strong gravity and the fine structure constant. In: Proceedings of the Indian Academy of Sciences Part A: Physical Sciences, 49 (2). pp. 352-358.
V. de Sabbata, C. Sivaram. Strong Spin-Torsion Interaction between Spinning Protons. Il Nuovo Cimento, Vol. 101A, N. 2, pp. 273-283 (1989).
T. R. Mongan. Cold dark matter from "strong gravity". General Relativity & Quantum Cosmology, 20 Jun 2007; arXiv:0706.3050v2.
Oldershaw R.L. Discrete Scale Relativity . Astrophysics and Space Science, Vol. 311, N. 4, pp. 431-433 (2007). http://dx.doi.org/10.1007/s10509-007-9557-x.
Stone R.A. Quark Confinement and Force Unification. Progress in Physics, Vol. 2, pp. 19-20 (2010).
K. Tennakone. Electron, muon, proton, and strong gravity. Phys. Rev. D, Volume 10, Issue 6, pp.1722-1725 (1974).
Zane Andrea Quintili. Gravitational Field and Proton Radius. vixra.org. (2019).
Recami, E.; Ammiraju, P.; Hernandez, H.E.; Kretly, L.C.; Rodrigues, W.A., Jr. Elementary particles as micro-universes: a geometric approach to "strong gravity". Apeiron, January 01, 1997.
Recami E. and Tonin-Zanchin V. The strong coupling constant: its theoretical derivation from a geometric approach to hadron structure. Found. Phys. Lett., v, 7(1), pp. 85-92 (1994).
Erasmo Recami, Tonin-Zanchin, Antonino Del Popolo, Mario Gambera. The strong coupling constant, Heavy Ion Physics, Vol. 10, pp. 345-349 (1999).
Stanislav Fisenko & Igor Fisenko. The Conception of Thermonuclear Reactor on the Principle of Gravitational Confinement of Dense High-temperature Plasma. Applied Physics Research, Vol. 2, No. 2, pp. 71-79 (2010).
S. I. Fisenko, M. M. Beilinson and B. G. Umanov. Some notes on the concept of “strong” gravitation and possibilities of its experimental investigation. Physics Letters A, Volume 148, Issues 8-9, pp. 405-407 (1990).
U. V. S. Seshavatharam and S. Lakshminarayana. Strong nuclear gravitational constant and the origin of nuclear planck scale. Progress in Physics, vol. 3, pp. 31-38 (2010). [2]
Perng J. J. Strong gravitation and elementary particles. Nuovo Cimento, Lettere, Serie 2, vol. 23, N. 15, pp. 552-554 (1978).
^а ^б Федосин С. Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1. (544 стр., Табл.66, Ил.93, Библ. 377 назв.).
Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012); статья на русском языке: Радиус протона в самосогласованной модели.
Комментарии к книге: Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009); статья на русском языке: Модель гравитационного взаимодействия в концепции гравитонов.
Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197 ; статья на русском языке: Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.
Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357; статья на русском языке: Заряженная компонента вакуумного поля как источник электрической силы в модернизированной модели Лесажа.

См. также

Внешние ссылки

· Strong gravitational constant

Источник: http://sergf.ru/psg.htm

На список страниц