Постоянная тонкой структуры

Постоянная тонкой структуры, обозначаемая α, является фундаментальной физической постоянной и константой взаимодействия, характеризующей силу электромагнитного взаимодействия. Как безразмерная численная величина α одна и та же во всех системах физических единиц. Впервые она была введена в 1916 году Арнольдом Зоммерфельдом. [1]

Значение α равно 7,29735257×10⁻³. ^[1]

Содержание

1 Определение
2 Боровская модель атома
3 См. также
4 Ссылки
5 Внешние ссылки

Определение

Имеется несколько эквивалентных определений α через другие физические постоянные:

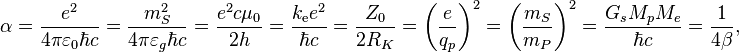
$\alpha ={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}}={\frac {m_{{S}}^{2}}{4\pi \varepsilon _{g}\hbar c}}={\frac {e^{2}c\mu _{0}}{2h}}={\frac {k_{{\mathrm {e}}}e^{2}}{\hbar c}}={\frac {Z_{0}}{2R_{K}}}=\left({\frac {e}{q_{p}}}\right)^{2}=\left({\frac {m_{S}}{m_{P}}}\right)^{2}={\frac {G_{s}M_{p}M_{e}}{\hbar c}}={\frac {1}{4\beta }},$

где:

e – элементарный заряд;
h – постоянная Планка;
ħ = h/2π – постоянная Дирака;
c – скорость света в вакууме;
ε₀ – электрическая постоянная;
m_S – масса Стони;
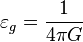$\varepsilon _{g}={\frac {1}{4\pi G}}$ – гравитоэлектрическая гравитационная постоянная, входящая в самосогласованные гравитационные константы;
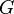– гравитационная постоянная;
µ₀ – магнитная постоянная;
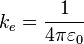$k_{e}={\frac {1}{4\pi \varepsilon _{0}}}$ – кулоновская константа;
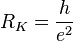$R_{K}={\frac {h}{e^{2}}}$ – постоянная фон Клитцинга;
Z₀ – волновое сопротивление вакуума;
q_p – заряд Планка;
m_P – масса Планка;
M_p – масса протона;
M_e – масса электрона;
G_s – постоянная сильной гравитации;
β – магнитная постоянная тонкой структуры. [2] ^[2]

В системе физических единиц СГС единица электрического заряда, статкулон или франклин, определён так, что кулоновская константа k_e равна 1 и безразмерна. В результате постоянная тонкой структуры выражается следующим типичным для старой физической литературы образом

$\alpha ={\frac {e^{2}}{\hbar c}}.$

Боровская модель атома

В боровской модели атома водорода α связана с параметрами атома в основном состоянии энергии

$~\alpha ={\frac {v_{B}}{c}},$

где $~v_{B}$ есть скорость движения вещества электрона при его вращении вокруг ядра на радиусе Бора $~a_{B}$ .

С другой стороны

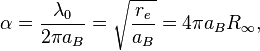
$~\alpha ={\frac {\lambda _{0}}{2\pi a_{B}}}={\sqrt {{\frac {r_{e}}{a_{B}}}}}=4\pi a_{B}R_{\infty },$

где $~\lambda _{0}\$ есть комптоновская длина волны электрона, $~r_{e}$ – классический радиус электрона, $~R_{\infty }$ – постоянная Ридберга для длины волны.

Следующее выражение для α имеет вид

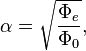
$~\alpha ={\sqrt {{\frac {\Phi _{{e}}}{\Phi _{0}}}}},$

где $~\Phi _{0}={\frac {h}{2e}}$ есть квант магнитного потока, $~\Phi _{e}=BS_{B}={\frac {\mu _{0}e}{4\pi a_{B}}}\sigma _{e}$ – магнитный поток электрона в основном состоянии, – магнитное поле в диске электрона с площадью поверхности $~S_{B}=\pi a_{B}^{2}$ , а $~\sigma _{e}={\frac {h}{2M_{e}}}$ есть квант циркуляции скорости для электрона. [3]

Ещё одно выражение α :

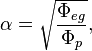
$~\alpha ={\sqrt {{\frac {\Phi _{{eg}}}{\Phi _{p}}}}},$

где $~\Phi _{p}={\frac {h}{2M_{p}}}=1.98\cdot 10^{{-7}}$ м²/с

есть квант потока поля кручения сильной гравитации протона, связанный с квантом циркуляции скорости протона,

$~\Phi _{{eg}}=\Omega S_{B}={\frac {G_{s}h}{2c^{2}a_{B}}}$

есть поток поля кручения сильной гравитации электрона в основном состоянии атома водорода, при этом $~\Omega$ есть поле кручения сильной гравитации в диске электрона.

Водородная система на уровне звёзд в боровской модели выражает α таким образом:

$~\alpha ={\frac {GM_{{ps}}M_{{\Pi }}}{\hbar _{s}C_{s}}},$

где $~M_{{ps}}$ и $~M_{{\Pi }}$ – масса звезды-аналога протона и масса планеты-аналога электрона, соответственно, $~\hbar _{s}$ – звёздная постоянная Дирака, $~C_{s}$ – характерная скорость вещества звезды.

См. также

Ссылки

"CODATA Value: fine-structure constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2011. Retrieved 2011-06-23.
Yakymakha O.L. (1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's. (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu .

Внешние ссылки