In English

Самосогласованные гравитационные константы

Материал из свободной русской энциклопедии «Традиция»

Самосогласованные гравитационные константы есть полный комплект фундаментальных констант, которые являются самосогласованными и определяют различные физические величины, связанные с гравитацией. Данные константы вычисляются таким же способом, как и электромагнитные константы в электродинамике. Это возможно благодаря тому, что в приближении слабого поля уравнения общей теории относительности переходят в уравнения гравитоэлектромагнетизма, аналогичные по форме уравнениям Максвелла. Точно также в приближении слабого поля уравнения ковариантной теории гравитации переходят в уравнения лоренц-инвариантной теории гравитации (ЛИТГ).^[1] Уравнениями ЛИТГ являются максвеллоподобные гравитационные уравнения, по форме совпадающие с уравнениями гравитоэлектромагнетизма. Если эти уравнения записывать с помощью самосогласованных гравитационных констант, возникает наибольшее подобие уравнений гравитационного и электромагнитного полей. Поскольку в 19 веке не было Международной системы единиц, первое упоминание о гравитационных константах вероятно сделал Forward (1961).^[^2]

Содержание

· 1 Определение

· 2 Связь с массой Планка и массой Стони

· 3 Связь с постоянной тонкой структуры

· 4 Квант потока поля кручения сильной гравитации

· 5 См. также

· 6 Ссылки

· 7 Внешние ссылки

Определение

В первичный набор гравитационных констант входят:

1. Первая гравитационная константа являющаяся скоростью гравитационных волн; ^[3]

2. Вторая гравитационная константа $~\rho_{g}$ , которая является гравитационным характеристическим импедансом вакуум (гравитационным волновым сопротивлением вакуума).

Во вторичный набор гравитационных констант входят:

1. Гравитоэлектрическая константа (подобно электрической постоянной): $~\varepsilon_g = \frac{1}{4\pi G } = 1,192708\cdot 10^9$ кг∙ с² ∙м^–3, где – гравитационная постоянная.

2. Гравитомагнитная константа (подобно магнитной постоянной): $~\mu_g = \frac{4\pi G }{ c^2_{g}}.$

Если скорость гравитации равна скорости света, $~ c_{g}=c,$ то ^[2] $~\mu_{g0} = 9,328772\cdot 10^{-27}$ м / кг.

Первичный и вторичный наборы гравитационных констант являются самосогласованными, поскольку они связаны следующими соотношениями:

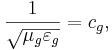
$~\frac{1}{\sqrt{\mu_g\varepsilon_g}} = c_g ,$

$~\sqrt{\frac{\mu_g}{\varepsilon_g}} = \rho_{g} = \frac{4\pi G }{c_g}.$

Если $~ c_{g}=c,$ то гравитационный характеристический импеданс пустого пространства будет равен: ^[5] ^[6]

$~ \rho_{g0} = \frac{4\pi G }{c} = 2,796696\cdot 10^{-18}$ м² /(с ∙ кг).

В лоренц-инвариантной теории гравитации величина $~ \rho_g$ содержится в формуле для вектора плотности потока энергии гравитационного поля (смотри вектор Хевисайда): ^[3]

$~ \mathbf{H} = -\frac{ c^2_g }{4 \pi G } \mathbf{\Gamma }\times \mathbf{\Omega} = -\frac{ c_g }{\rho_g }\mathbf{\Gamma }\times \mathbf{\Omega},$

где:

$~ \mathbf{\Gamma }$ есть напряжённость гравитационного поля или гравитационное ускорение,

$~ \mathbf{\Omega}$ есть поле кручения .

Для плоской поперечной однородной гравитационной волны, в которой для амплитуд напряжённостей полей выполняется соотношение $~\Gamma = c_g \Omega$ , можно записать:

$~H = \frac{ \Gamma^2 }{\rho_g }.$

Аналогичное соотношение в электродинамике для амплитуды потока плотности электромагнитной энергии плоской электромагнитной волны в вакууме, в которой , имеет вид: ^[7]

$~S = \frac{ E^2 }{Z_0 },$

где $~ \mathbf {S} = \frac {\mathbf{E}\times \mathbf{B} }{\mu_0} = \frac {c}{Z_0}\mathbf{E}\times \mathbf{B}$ – вектор Пойнтинга, – напряжённость электрического поля, – магнитная индукция,

$~ \mu_0$ – магнитная постоянная, $~ Z_0 = c \mu_0$ – электромагнитное волновое сопротивление вакуума.

Гравитационное волновое сопротивление вакуума $~\rho _{{g0}}$ было использовано в статье ^[8] для оценки сечения взаимодействия гравитонов с веществом.

Связь с массой Планка и массой Стони

Поскольку гравитационная постоянная и скорость света входят в планковскую массу $m_P = \sqrt{\frac{\hbar c}{ G }}\$ , где $~ \hbar$ – постоянная Дирака, то гравитационный характеристический импеданс пустого пространства можно представить так:

$~ \rho_{g0} = \frac{2h}{m_{P}^2}$ ,

где – постоянная Планка.

Существует ещё масса Стони , связанная с элементарным электрическим зарядом и электрической постоянной $~ \varepsilon_0$ :

$~m_S = e\sqrt{\frac{\varepsilon_g}{\varepsilon_0}} = \frac{e}{\sqrt{4\pi G \varepsilon_0}}$ .

Масса Стони может быть выражена через планковскую массу:

$~m_S = \sqrt{\alpha}\cdot m_P$ ,

где $~ \alpha$ есть электрическая постоянная тонкой структуры.

Отсюда следует ещё одно выражение для гравитационного характеристического импеданса пустого пространства:

$~ \rho_{g0} = \alpha \cdot \frac{2h}{m_{S}^2}$ .

Закон Ньютона для гравитационной силы притяжения двух масс Стони может быть записан так:

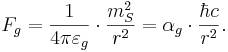
$~F_g = \frac{1}{4\pi \varepsilon_g}\cdot \frac{m_{S}^2}{r^2}= \alpha_g \cdot \frac{\hbar c}{r^2}.$

Закон Кулона для электрической силы между двумя элементарными зарядами имеет вид:

$~F_e = \frac{1}{4\pi \varepsilon_0}\cdot \frac{e^2}{r^2}= \alpha \cdot \frac{\hbar c}{r^2}.$

Равенство и приводит к соотношению для массы Стони $~m_S = e\sqrt{\frac{\varepsilon_g}{\varepsilon_0}},$ указанному выше. Следовательно масса Стони может быть определена из условия, что две такие массы взаимодействуют посредством гравитации с такой же силой, как если бы эти массы имели заряды, равные элементарному заряду, и взаимодействовали посредством только электромагнитных сил.

Связь с постоянной тонкой структуры

Электрическая постоянная тонкой структуры равна:

$~\alpha = \frac{e^2}{2\varepsilon_0 hc}.$

Аналогично можно ввести соответствующую величину для гравитации: $~\alpha_g = \frac{m_{S}^2}{2\varepsilon_g hc}=\alpha ,$ с равенством обеих постоянных тонкой структуры по величине.

С другой стороны, гравитационная постоянная тонкой структуры для водородной системы и на уровне атомов и на уровне звёзд также равна электрической постоянной тонкой структуры:

$~\alpha ={\frac {G_{s}M_{p}M_{e}}{\hbar c}}={\frac {GM_{{ps}}M_{{\Pi }}}{\hbar _{s}C_{s}}}={\frac {1}{137,036}}$ ,

где $~G_{s}$ – постоянная сильной гравитации, и – массы протона и электрона, $~ M_{ps}$ и $~ M_{\Pi }$ – массы звезды-аналога протона и планеты-аналога электрона соответственно, $~ \hbar_s$ – звёздная постоянная Дирака, – характерная скорость вещества звёзд.

Квант потока поля кручения сильной гравитации

Магнитная сила между двумя фиктивными элементарными магнитными зарядами равна:

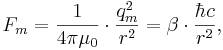
$F_m = \frac{1}{4\pi \mu_0}\cdot \frac{ q_m^2}{r^2} = \beta \cdot \frac{\hbar c}{r^2}, \$

где $q_m = \frac{h}{e} \$ есть магнитный заряд, $\beta = \frac {\varepsilon_0 h c}{2 e^2} = \frac {\pi \hbar}{c \mu_0 e^2}$ есть магнитная константа взаимодействия для фиктивных магнитных зарядов. ^[9]

Сила поля кручения между двумя фиктивными элементарными торсионными массами равна:

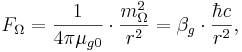
$F_{\Omega} = \frac{1}{4\pi \mu_{g0}}\cdot \frac{m_{\Omega }^2}{r^2} = \beta_g\cdot \frac{\hbar c}{r^2}, \$

где $\beta_g = \frac {\varepsilon_g h c}{2 m_S^2} = \frac {\pi \hbar}{c \mu_{g0} m_S^2} \$ есть торсионная константа взаимодействия для гравитационной торсионной массы $m_{\Omega } \$ .

При равенстве вышеуказанных сил находится равенство констант взаимодействия для магнитного поля и поля кручения:

$\beta = \beta_g = \frac{1}{4\alpha}, \$

из которого находится масса Стони $m_S \$ и гравитационная торсионная масса:

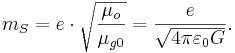
$m_S = e \cdot \sqrt {\frac{\mu_o}{\mu_{g0}}} = \frac{e}{\sqrt {4 \pi \varepsilon_0 G}}. \$

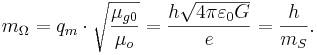
$m_{\Omega } = q_m \cdot \sqrt {\frac{\mu_{g0}}{\mu_o }} = \frac{h \sqrt {4 \pi \varepsilon_0 G}}{e }=\frac {h}{m_S} . \$

Вместо фиктивного элементарного магнитного заряда $q m$ $=$ $h$ $/$ $e$ в квантовой механике более важен квант магнитного потока $\Phi_0 = h/(2e) \approx 2,067833758 (46) \cdot 10^{-15}$ Вб. ^[10] С другой стороны на уровне атомов действует сильная гравитация и необходимо использовать постоянную сильной гравитации. В этом случае должен быть важным квант потока поля кручения сильной гравитации:

$\Phi _{\Gamma }={\frac {h}{2e}}{\sqrt {{\frac {4\pi \varepsilon _{0}G_{s}M_{e}}{M_{p}}}}}={\frac {h}{2M_{p}}}=1,98\cdot 10^{{-7}}$ м²/с,

который связан с массой протона $M p$ и его квантом циркуляции скорости.

См. также

Лоренц-инвариантная теория гравитации
Гравитоэлектромагнетизм
Скорость гравитации
Максвеллоподобные гравитационные уравнения
Квантовый гравитационный резонатор
Квант циркуляции скорости
Электродинамика
Гравитационная волна

Ссылки

Федосин С.Г. Физические теории и бесконечная вложенность материи, Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
R. L. Forward, Proc. IRE 49, 892 (1961).
^а ^б Федосин С.Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, (544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1).
Kiefer, C.; Weber, C. On the interaction of mesoscopic quantum systems with gravity. Annalen der Physik, 2005, Vol. 14, Issue 4, Pages 253 – 278.
J. D. Kraus, IEEE Antennas and Propagation. Magazine 33, 21 (1991).
Raymond Y. Chiao. "New directions for gravitational wave physics via “Millikan oil drops” arXiv:gr-qc/0610146v16 (2007).PDF
Иродов И.Е. Основные законы электромагнетизма. Учебное пособие для студентов вузов. 2- издание. М.: Высшая школа, 1991.

8. Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, P. 1 – 18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197. // Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.

9. Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kiev: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu.

"Magnetic flux quantum Φ0". 2010 CODATA recommended values. Retrieved 10 January 2012

Внешние ссылки

Selfconsistent gravitational constants

Источник: http://sergf.ru/sk.htm

На список страниц