Acceleration stress-energy tensor

Acceleration stress-energy tensor is a symmetric four-dimensional tensor of second valence (rank), which describes the energy density and energy flux density of an acceleration field in matter. This tensor in covariant theory of gravitation is included in equation for determining the metric along with gravitational stress-energy tensor, pressure stress-energy tensor, dissipation stress-energy tensor and stress-energy tensor of electromagnetic field. The covariant derivative of the acceleration stress-energy tensor determines density of four-force acting on matter particles.

1 Covariant theory of gravitation

1.1 Definition
1.2 Components of acceleration stress-energy tensor
1.3 4-force density and field equation
1.4 Equation for metric
1.5 Equation of motion
1.6 Conservation laws

2 Relativistic mechanics
3 See also
4 References
5 External links

Covariant theory of gravitation

Definition

In covariant theory of gravitation (CTG) the acceleration field is not a scalar field and considered as 4-vector field, 4-potential of which consists of the scalar and 3-vector components. In CTG the acceleration stress-energy tensor was defined by Fedosin through the acceleration tensor $~ u_{ik}$ and the metric tensor $~ g^{ik}$ by the principle of least action: ^[1]

$~ B^{ik} = \frac{c^2} {4 \pi \eta } \left( - g^{im} u_{nm} u^{nk}+ \frac {1} {4} g^{ik}u_{mr}u^{mr}\right) ,$

where $~ \eta$ is the acceleration field constant defined in terms of the fundamental constants and physical parameters of the system. Acceleration field is considered as a component of the general field.

Components of acceleration stress-energy tensor

Since acceleration tensor consists of the components of the acceleration field strength $~ \mathbf {S}$ and the solenoidal acceleration vector $~ \mathbf {N}$ , then the acceleration stress-energy tensor can be expressed through these components. In the limit of special relativity the metric tensor ceases to depend on the coordinates and time, and in this case the acceleration stress-energy tensor gains the simplest form:

$~B^{{ik}}={\begin{vmatrix}\varepsilon _{a}&{\frac {K_{x}}{c}}&{\frac {K_{y}}{c}}&{\frac {K_{z}}{c}}\\{\frac {K_{x}}{c}}&\varepsilon _{a}-{\frac {S_{x}^{2}+c^{2}N_{x}^{2}}{4\pi \eta }}&-{\frac {S_{x}S_{y}+c^{2}N_{x}N_{y}}{4\pi \eta }}&-{\frac {S_{x}S_{z}+c^{2}N_{x}N_{z}}{4\pi \eta }}\\{\frac {K_{y}}{c}}&-{\frac {S_{x}S_{y}+c^{2}N_{x}N_{y}}{4\pi \eta }}&\varepsilon _{a}-{\frac {S_{y}^{2}+c^{2}N_{y}^{2}}{4\pi \eta }}&-{\frac {S_{y}S_{z}+c^{2}N_{y}N_{z}}{4\pi \eta }}\\{\frac {K_{z}}{c}}&-{\frac {S_{x}S_{z}+c^{2}N_{x}N_{z}}{4\pi \eta }}&-{\frac {S_{y}S_{z}+c^{2}N_{y}N_{z}}{4\pi \eta }}&\varepsilon _{a}-{\frac {S_{z}^{2}+c^{2}N_{z}^{2}}{4\pi \eta }}\end{vmatrix}}.$

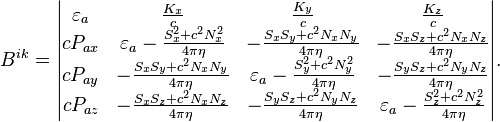
The time-like components of the tensor denote:

1) The volumetric energy density of acceleration field

$~ B^{00} = \varepsilon_a = \frac{1}{8 \pi \eta }\left(S^2+ c^2 N^2 \right).$

2) The vector of energy flux density of acceleration field is

$~\mathbf{K} = \frac{ c^2 }{4 \pi \eta }[\mathbf{S}\times \mathbf{N}].$

The components of the vector $~{\mathbf {K}}$ are part of the corresponding tensor components $B^{{01}}$ , $B^{{02}}$ , $B^{{03}}$ .

Due to symmetry of the tensor indices, $B^{{01}}=B^{{10}},B^{{02}}=B^{{20}},B^{{03}}=B^{{30}}$ .

3) The space-like components of the tensor form a submatrix 3 x 3, which is the 3-dimensional acceleration stress tensor, taken with a minus sign. The acceleration stress tensor can be written as

$~ \sigma^{p q} = \frac {1}{4 \pi \eta } \left( S^p S^q + c^2 N^p N^q - \frac {1}{2} \delta^{pq} (S^2 + c^2 N^2 ) \right) ,$

where the components the Kronecker delta $~\delta^{pq}$ equals 1 if and equals 0 if $~p \not=q.$

Three-dimensional divergence of stress tensor of acceleration field connects force density and rate of change of energy flux density of acceleration field:

$~ \partial_q \sigma^{p q} = - f^p +\frac {1}{c^2} \frac{ \partial K^p}{\partial t},$

where denote the components of the three-dimensional acceleration force density, – the components of the energy flux density of the acceleration field.

4-force density and field equation

The principle of least action implies that the 4-vector of force density $~f_{\alpha }$ can be found through the acceleration stress-energy tensor, either through the product of acceleration tensor and mass 4-current:^[2]

$~f_{\alpha }=\nabla _{\beta }{B_{\alpha }}^{\beta }=-u_{{\alpha k}}J^{k}.\qquad (1)$

The field equations of acceleration field are as follows:

$~ \nabla_n u_{ik} + \nabla_i u_{kn} + \nabla_k u_{ni}=0,$

$~\nabla_k u^{ik} = -\frac {4 \pi \eta }{c^2} J^i .$

In the special theory of relativity, according to (1) for the components of the four-force density can be written:

$~f_{\alpha }=(-{\frac {{\mathbf {S}}\cdot {\mathbf {J}}}{c}},-{\mathbf {f}}),$

where $~ \mathbf{f}= - \rho \mathbf{S} - [\mathbf{J} \times \mathbf{N} ]$ is the 3-vector of the force density, $~\rho$ is the density of the moving matter, $~\mathbf{J} =\rho \mathbf{v}$ is the 3-vector of the mass current density, $~\mathbf{v}$ is the 3-vector of velocity of the matter unit.

In Minkowski space, the field equations are transformed into four equations for the acceleration field strength $~ \mathbf {S}$ and solenoidal acceleration vector $~ \mathbf {N}$

$~\nabla \cdot \mathbf{ S} = 4 \pi \eta \rho,$

$~\nabla \times \mathbf{ N} = \frac {1 }{c^2}\frac{\partial \mathbf{ S}}{\partial t}+\frac {4 \pi \eta \rho \mathbf{ v}}{c^2},$

$~\nabla \cdot \mathbf{ N} = 0,$

$~\nabla \times \mathbf{ S} = - \frac{\partial \mathbf{ N}}{\partial t}.$

Equation for metric

In the covariant theory of gravitation the acceleration stress-energy tensor in accordance with the principles of metric theory of relativity is one of the tensors defining metrics inside the bodies by the equation for the metric:

$~ R_{ik} - \frac{1} {4 }g_{ik}R = \frac{8 \pi G \beta }{ c^4} \left( B_{ik}+ P_{ik}+ U_{ik}+ W_{ik} \right),$

where $~ \beta$ is the coefficient to be determined, $~ B_{ik}$ , $~ P_{ik}$ , $~ U_{ik}$ and $~ W_{ik}$ are the stress-energy tensors of the acceleration field, pressure field, gravitational and electromagnetic fields, respectively, is the gravitational constant.

Equation of motion

The equation of motion of a point particle inside or outside matter can be represented in tensor form, with acceleration stress-energy tensor $B^{ik}$ or acceleration tensor $u_{nk}$ :

$~ - \nabla_k \left( B^{ik}+ U^{ik} +W^{ik}+ P^{ik} \right) = g^{in}\left(u_{nk} J^k + \Phi_{nk} J^k + F_{nk} j^k + f_{nk} J^k \right) =0. \qquad (2)$

where $~ \Phi_{nk}$ is the gravitational tensor , $~F_{nk}$ is the electromagnetic tensor, $~ f _{nk}$ is the pressure field tensor, $~j^k = \rho_{0q} u^k$ is the charge 4-current, $~\rho_{0q}$ is the density of electric charge of the matter unit in the reference frame at rest, is the 4-velocity.

We now recognize that $~ J^k = \rho_{0} u^k$ is the mass 4-current and the acceleration tensor is defined through the covariant 4-potential as $~u_{{nk}}=\nabla _{n}U_{k}-\nabla _{k}U_{n}.$ This gives the following: ^[3]

$~\nabla _{\beta }{B_{n}}^{\beta }=-u_{{nk}}J^{k}=-\rho _{{0}}u^{k}(\nabla _{n}U_{k}-\nabla _{k}U_{n})=\rho _{{0}}{\frac {DU_{n}}{D\tau }}-\rho _{{0}}u^{k}\nabla _{n}U_{k}.\qquad (3)$

Here operator of proper-time-derivative $~u^{k}\nabla _{k}={\frac {D}{D\tau }}$ is used, where is the symbol of 4-differential in curved spacetime, $~ \tau$ is the proper time, $~ \rho_0$ is the mass density in the comoving frame.

Accordingly, the equation of motion (2) becomes:

$~\rho _{{0}}{\frac {DU_{n}}{D\tau }}-\rho _{{0}}u^{k}\nabla _{n}U_{k}=-\nabla ^{k}\left(U_{{nk}}+W_{{nk}}+P_{{nk}}\right)=\Phi _{{nk}}J^{k}+F_{{nk}}j^{k}+f_{{nk}}J^{k}.$

Time-like component of the equation at describes the rate of change of the scalar potential of the acceleration field, and spatial component at connects the rate of change of the vector potential of the acceleration field with the force density.

Conservation laws

When the index in (2), i.e. for the time-like component of the equation, in the limit of special relativity from the vanishing of the left side of (2) follows:

$~ \nabla \cdot (\mathbf{ K }+ \mathbf{H}+\mathbf{P}+ \mathbf{F} ) = -\frac{\partial (B^{00}+U^{00}+W^{00}+P^{00} )}{\partial t},$

where $~ \mathbf{ K }$ is the vector of acceleration field energy flux density, $~ \mathbf{H}$ is the Heaviside vector, $~ \mathbf{ P }$ is the Poynting vector, $~ \mathbf{F}$ is the vector of pressure field energy flux density.

This equation can be regarded as a local conservation law of energy and energy flux of the four fields. ^[4]

The integral form of the law of conservation of energy and energy flux is obtained by integrating (2) over the 4-volume. By the divergence theorem the integral of the 4-divergence of some tensor over the 4-space can be replaced by the integral of time-like tensor components over 3-volume. As a result, in Lorentz coordinates the integral vector equal to zero may be obtained: ^[5]

$~{\mathbb {Q}}^{i}=\int {\left(B^{{i0}}+U^{{i0}}+W^{{i0}}+P^{{i0}}\right)dV}.$

Vanishing of the integral vector allows us to explain the 4/3 problem, according to which the mass-energy of field in the flux of field of the moving system in 4/3 more than in the field energy of fixed system. On the other hand, according to, ^[4] the generalized Poynting theorem and the integral vector should be considered differently inside the matter and beyond its limits. As a result, the occurrence of the 4/3 problem is associated with the fact that the time components of the stress-energy tensors do not form four-vectors, and therefore they cannot define the same mass in the fields’ energy and flux energy in principle. In ^[6] it is shown that the integral vector does not provide the possibility of finding the 4-momentum of a physical system. However, the energy and momentum, which are components of the 4-momentum, can be found in covariant form. In this case, the state of the physical system is determined through the 4-momentum of the center of momentum of the system.

General relativity

In general relativity (GR), the acceleration stress-energy tensor is not used. Instead, it uses the so-called stress-energy tensor of matter, which in the simplest case has the following form: $~ \phi_{ n \beta }= \rho_0 u_n u_\beta$ . In GR, the tensor $~ \phi_{ n \beta }$ is substituted into the equation for the metric and its covariant derivative gives the following:

$~ \nabla^\beta \phi _{n \beta} = \nabla^\beta (\rho_0 u_n u_\beta) = u_n \nabla^\beta J_\beta + \rho_0 u_\beta \nabla^\beta u_n .$

If we assume that the continuity equation is satisfied in the form $~\nabla ^{\beta }J_{\beta }=0,$ then, using the operator of proper-time-derivative the covariant derivative of the tensor $~ \phi_{ n \beta }$ gives the product of the mass density and four-acceleration, i.e. the density of 4-force:

$~\nabla ^{\beta }\phi _{{n\beta }}=\rho _{0}u_{\beta }\nabla ^{\beta }u_{n}=\rho _{0}u^{\beta }\nabla _{\beta }u_{n}=\rho _{0}{\frac {Du_{n}}{D\tau }}.\qquad (4)$

Unlike (4), in the covariant theory of gravitation, equation (3) for divergence of the acceleration stress-energy tensor $~{B_{n}}^{\beta }$ contains an additional term on the right-hand side.

References

^1.0 ^1.1 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30 (2016).
Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
^3.0 ^3.1 Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12.
Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.

External links

Acceleration stress-energy tensor in Russian

Source: http://sergf.ru/asen.htm

На русском языке