Gravitational four-potential

Gravitational four-potential is a four-vector function (4-vector), by which the properties of gravitational field are determined in the Lorentz-invariant theory of gravitation, ^[1] as well as in the covariant theory of gravitation. ^[2] The gravitational 4-potential includes the scalar and vector potentials of gravitational field. During the gauge transformation the potentials of the gravitational field can change their form so that non-coinciding 4-potentials with different dependence on the coordinates and time can correspond to the same gravitational field.

1 Definition
2 Relation with the gravitational field strength and the torsion field
3 Gauge fixing of the 4-potential
4 Solution of the wave equation for the 4-potential
5 Lagrangian and action
6 The role of the 4-potential in the theory of gravitation
7 See also
8 References
9 External links

Definition

Gravitational 4-potential, like any 4-vector, consists of the scalar and vector parts, which in sum give 4 components:

$~D_\mu = \left( \frac {\psi }{ c_{g}}, -\mathbf{D} \right) = \left( \frac {\psi }{ c_{g}}, -D_x, -D_y, -D_z \right).$

The time-like component of the 4-potential is the scalar potential $~\psi$ , divided by the speed of gravitation $~ c_{g}$ . The space-like component of the 4-potential is represented by the vector potential of gravitational field $~ \mathbf{D}$ , which has three components.

Definition of the 4-potential $~D_\mu$ in the covariant representation with a lower index is preferred to the contravariant representation (with an upper index), as it makes the solution of equations easier.

In the transition from one reference frame to another the 4-potential is transformed in accordance with the axioms of the metric theory of relativity. In case of Minkowski space of the special theory of relativity transformations of the 4-potential are performed from one inertial frame to another using Lorentz transformations.

In the international system of units SI the gravitational 4-potential $~D_\mu$ is measured in m/s, in the system of physical units CGS – in cm/s.

Relation with the gravitational field strength and the torsion field

By the gravitational 4-potential the gravitational tensor is determined, for this purpose a 4-rotor is used:

$~ \Phi_{\mu \nu} = \nabla_\mu D_\nu - \nabla_\nu D_\mu = \partial _\mu D_\nu - \partial _\nu D_\mu =\frac{\partial D_\nu}{\partial x^\mu} - \frac{\partial D_\mu}{\partial x^\nu}.\qquad (1)$

The antisymmetric tensor $~ \Phi_{\mu \nu}$ contains only 6 components, three of which are associated with the vector of gravitational field strength $~ \mathbf{\Gamma }$ , and the other three components – with the vector of the gravitational torsion field $~ \mathbf{\Omega}$ . In Cartesian coordinates these vectors are obtained as follows:

$~\mathbf{\Gamma }= -\nabla \psi - \frac{\partial \mathbf{D}} {\partial t}.$

$~\mathbf{\Omega }= \nabla \times \mathbf{D}.$

From the latter relation we see that the torsion field depends only on the vector potential. At the same time, contribution into the gravitational field strength is made not only by the gradient of the scalar potential, but also by the rate of change in time of the vector potential.

Gauge fixing of the 4-potential

The most convenient is the gauge, when the 4-divergence of the 4-potential is zero:

$~ \nabla_\mu D^\mu =\nabla^\mu D_\mu=0.$

In the special relativity the covariant derivative $~ \nabla_\mu$ becomes a partial derivative $~ \partial_\mu$ . This allows us to represent the gauge condition explicitly as follows:

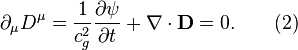
$~ \partial_\mu D^\mu = \frac {1}{c^2_g} \frac {\partial \psi}{\partial t} + \nabla \cdot \mathbf{D} =0. \qquad (2)$

In the Lorentz-invariant theory of gravitation the Heaviside equations for gravitational field are written in the four-dimensional form:

$~ \partial^k \Phi_{ik} = \frac {4 \pi G }{c^2_{g}} J_i , \qquad (3)$

$~ \partial_n \Phi_{ik} + \partial_i \Phi_{kn} + \partial_k \Phi_{ni}=0. \qquad (4)$

It can be shown that the gauge condition of the 4-potential (2) follows from the definition of the gravitational tensor (1) and the field equations (3) and (4). If we apply the partial derivative $~ \partial^k$ to (4), then its action in the first two terms in (4) on the tensor $~ \Phi_{ik}$ can be considered with the help of (3). For the third term in (4) we obtain the relation $~ \partial^k \partial_k = \Box$ , where $~ \Box$ is the 4-d'Alembertian operator:

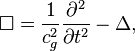
$~ \Box = \frac {1}{c^2_g} \frac {\partial^2 }{\partial t^2}- \Delta,$

here the Laplace operator is applied, which in Cartesian coordinates has the form $~ \Delta= \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}.$

Substituting in (4) $~ \Phi_{ni}$ with its expression according to (1), from (4) as a simplest option we obtain the wave equation for the 4-potential, the source of which is the mass 4-current : ^[3]

$~\Box D_i = -\frac {4 \pi G }{c^2_{g}} J_i, \qquad (5)$

where is the gravitational constant.

On the other hand, if in (3) we substitute $~ \Phi_{ik}$ with its expression according to (1), we obtain again the wave equation (5) for the 4-potential, but only given the gauge conditions of the 4-potential (2) is met. Thus, due to the symmetry of fields, this calibration can simplify the field equations.

Note that if we take the partial derivative $~ \partial^i$ of both sides in (3), then taking into account (1) the left side is equal to zero. Then from the equality of the right side to zero the continuity equation follows for the mass 4-current:

$~ \partial^i J_i=0.$

If we subtract from the gravitational 4-potential the gauge 4-vector of the form $~\chi_i = \nabla _i \chi$ , depending on a scalar gauge function $~ \chi$ , then provided that the function $~ \chi$ satisfies the wave equation

$~\Box \chi = 0,$

for the new 4-potential $~ D^\prime_i = D_i -\chi_i$ the gauge condition (2) will remain in force, and the gravitational tensor according to (1) will not change its form. Thus, the Lorentz-invariant theory of gravitation and built upon it the covariant theory of gravitation are gauge theories.

In the covariant theory of gravitation the Heaviside equations (3) and (4) for gravitational field are generalized for the curved spacetime and are written in such form: ^[2]

$~\nabla^k \Phi_{ik} = \frac {4 \pi G }{c^2_{g}} J_i ,$

$~ \nabla_n \Phi_{ik} + \nabla_i \Phi_{kn} + \nabla_k \Phi_{ni}=0.$

The continuity equation for the mass 4-current becomes dependent on Ricci tensor $R_{ \mu \alpha }$ : ^[4]

$~ R_{ \mu \alpha } \Phi^{\mu \alpha }= -\frac {4 \pi G }{c^2_g} \nabla_{\alpha}J^{\alpha}.$

Wave equation instead of (5) is as follows:

$~ g^{ik}\partial_i \partial_k D^s + g^{ik}( \Gamma^s_{kr}\partial_i D^r - \Gamma^r_{ik}\partial_r D^s + \Gamma^s_{ri}\partial_k D^r + D^r \partial_r \Gamma^s_{ki} ) =-\frac {4 \pi G }{c^2_g} J^s .$

In the curved spacetime in the equation we should take into account mixing of the vector components. In particular, the scalar potential of gravitational field becomes the function not only of the mass density $~ \rho$ , but also of the mass current density $~ \mathbf {J} = \rho \mathbf {V}$ , where $~ \mathbf {V}$ is the velocity of the matter.

Solution of the wave equation for the 4-potential

In the special theory of relativity, the Christoffel symbols $\Gamma^s_{kr}$ are zero, and then the solution of the wave equation can be simplified so that it can be represented as follows: ^[2]

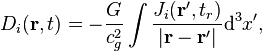
$~ D_i (\mathbf{r}, t) = -\frac{G}{c^2_g} \int \frac{J_i ( \mathbf{r}^\prime, t_r)}{ \left| \mathbf{r} - \mathbf{r}^\prime \right|} \mathrm{d}^3 x^\prime ,$

where the gravitational 4-potential at the time point at the point of the space determined by the radius vector $~ \mathbf{r}$ , is found by integrating over the volume, containing the mass 4-current (or 4-vector of mass current density) . In this case integration over the volume is carried out for an earlier point in time $~t_r = t - \frac{\left|\mathbf{r}-\mathbf{r}'\right|}{c_g}$ , where $~\mathbf{r}^\prime$ is the radius vector that specifies the location of the mass 4-current at the earlier time, is the speed of gravitation.

From the given solution for the time-like components of 4-vectors we can see that the scalar potential depends on the mass density of a certain moving particle at the earlier point in time and on the distance from this particle to the point where the potential is measured. In turn, the vector potential also depends on the speed of the particle at the earlier point in time. The presence of the volume integral implies that for the potentials of gravitational field the superposition principle holds, and for calculating the total 4-potential we should take into account all sources of the field.

The 4-potential of the proper gravitational field of a single solid point particle can be obtained in another way – by multiplying the scalar gravitational potential $~ \psi_0$ around this particle, calculated in the reference frame co-moving with this particle, by the 4-velocity of the point particle:

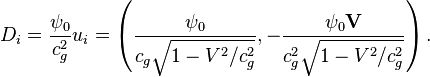
$~ D_i = \frac {\psi_0}{c^2_{g}} u_i = \left( \frac {\psi_0}{c_g \sqrt {1-V^2/c^2_g}}, - \frac {\psi_0 \mathbf {V}}{c^2_g \sqrt {1-V^2/c^2_g}} \right) .$

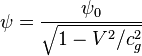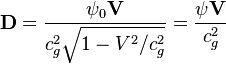For the observer, relative to which the point particle is moving, according to the Lorentz transformations the scalar potential changes due to the motion of the particle: $~ \psi =\frac {\psi_0}{\sqrt {1-V^2/c^2_g}}$ , and also the vector potential appears, which is equal to $~ \mathbf {D} = \frac {\psi_0 \mathbf {V}}{c^2_g \sqrt {1-V^2/c^2_g}}=\frac {\psi \mathbf {V}}{c^2_g }$ . This gives the ordinary definition of the gravitational 4-potential in the form

$~ D_i = \left( \frac {\psi}{c_g}, - \mathbf {D} \right) .$

Indeed, the 4-potential of any vector field for a single particle, inside which the vector potentials of the fields are absent, can be represented as follows: ^[5]^[6]

$~ L_\mu = \frac { k_f \varepsilon_p }{\rho_0 c^2} u_\mu ,$

where $~ k_f = \frac {\rho_0}{\rho_{0q}}$ for electromagnetic field and for other fields, $~ \rho_{0}$ and $~\rho_{0q}$ are the mass density and accordingly charge density in comoving reference frame, $~ \varepsilon_p$ is the field energy density of the particle, $~ u_\mu$ is the covariant four-velocity.

For gravitational field $~ \varepsilon_p = \psi_0 \rho_0$ , , and assuming equality of the speed of light and the speed of gravity , we arrive to formulas for the 4 potential , shown above.

In a system of a set of point particles composing material bodies, in order to find the total 4-potential we should add 4-potentials of all point particles, taking into account the differences in their 4-velocities and their different location in space. As a result the total vector potential of the system of particles only indirectly reflects the total scalar potential of the given system of particles, in contrast to the direct relation between the scalar and vector potentials of an individual point particle. In the case of calculating the total 4-potential of a massive solid body, given the different distances from the parts of the body to the point where the 4-potential is defined, we obtain the gravitational Liénard–Wiechert potential. ^[7]^[8]

Lagrangian and action

The gravitational 4-potential is part of the Lagrangian for the matter in gravitational and electromagnetic fields that allows us to write the corresponding action function: ^[9] ^[4]

$~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}D_\mu J^\mu + \frac {c}{16 \pi G} \Phi_{ \mu\nu}\Phi^{ \mu\nu} -\frac {1}{c}A_\mu j^\mu - \frac {c \varepsilon_0}{4} F_{ \mu\nu}F^{ \mu\nu}-$

$~ -\frac {1}{c}u_\mu J^\mu - \frac {c }{16 \pi \eta } u_{ \mu\nu}u^{ \mu\nu} -\frac {1}{c} \pi_\mu J^\mu - \frac {c }{16 \pi \sigma } f_{ \mu\nu}f^{ \mu\nu} ) \sqrt {-g}d\Sigma,$

where is Lagrangian, is the time differential of the reference frame used, is a certain coefficient, is the scalar curvature, $~\Lambda$ is the cosmological constant, which characterizes the energy density of the considered system as a whole and therefore is the function of the system, is the speed of light as a measure of the propagation speed of electromagnetic and gravitational interactions, the electromagnetic 4-potential $~ A_\mu = \left( \frac {\varphi }{ c}, -\mathbf{A}\right)$ where $~\varphi$ is the scalar potential, and $~\mathbf{A}$ is the vector potential, $~ j^\mu$ – electric four-current, $~\varepsilon_0$ is the electric constant, $~ F_{ \mu\nu}$ – electromagnetic tensor, $~ u_{ \mu\nu}$ – acceleration tensor, $~ \eta$ and $~ \sigma$ are some constants, $~ \pi_\mu$ is four-potential of pressure field, $~ f_{ \mu\nu}$ – pressure field tensor, $~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3$ is the invariant 4-volume expressed through the differential of the time coordinate , through the product of differentials of the space coordinates, and through the square root $~\sqrt {-g}$ of the determinant of the metric tensor taken with a negative sign.

In the action integral the gravitational 4-potential is present within the invariant $~ D_\mu J^\mu$ , and as well as part of the gravitational field tensor $~ \Phi_{ \mu\nu}$ and its invariant $~ \Phi_{ \mu\nu}\Phi^{ \mu\nu}$ . In the first case, the 4-potential determines the function of the binding energy of the substance and the field, and in the second case it determines the energy function of the field as an independent object. The variation of the action function leads to the determination of the gravitational stress-energy tensor of the gravitational field, sets the gravitational field equations (3) and (4), the equation of the substance motion in the field and the expression for the gravitational four-force.

The role of the 4-potential in the theory of gravitation

In classical mechanics instead of the total 4-potential its scalar component is used in the form of the gravitational potential. This allows us to find the potential gravitational energy of bodies and the equations of their motion. In order to calculate the scalar gravitational potential the Poisson equation is used of the form: $~\Delta \psi=-4 \pi G \rho$ , where $~\Delta$ is the Laplace operator, $~\rho$ is the volume density of the mass distribution at the considered point. However, the expressions obtained for the potential, forces and energies are not Lorentz covariant, that is, the problem arises during the translation of the results from one inertial frame to another.

The gravitational 4-potential practically is not considered in the general relativity (GR). This is due to the fact that in GR the gravitational field is considered identical to the metric field, and the components of the metric tensor are used as the gravitational potentials, and the Christoffel symbols are used instead of the field strength. In the weak field the relation can be established between the component $~g_{00}$ of the metric tensor of the spacetime and the gravitational scalar potential in classical mechanics: $~g_{00}\approx 1+ \frac {2 \psi}{c^2}$ , where is the speed of light. The vector potential of gravitational field $~ \mathbf{D}$ that is used in the Lorentz-invariant theory of gravitation can also be expressed in terms of the components of the metric tensor of GR.

On the other hand, in the axiomatic construction of the Lorentz-invariant theory of gravitation (LITG) it is the 4-potential $~ D_\mu$ that represents the gravitational field, while as for the substance it is represented by the mass 4-current $~ J^\mu$ . The fifth axiom of LITG states that d'Alembertian of the 4-potential equals the mass 4-current with a corresponding constant factor. ^[2] It is sufficient to derive all of the relations of the Lorentz-invariant theory of gravitation. The axiomatics of LITG is the same for the covariant theory of gravitation (CTG), since CTG is the generalization of LITG to the curved spacetime, in which the metric tensor is dependent on the time and coordinates.

The gravitational 4-potential as well as the electromagnetic 4-potential, acting on test bodies, influences the rate of time in these bodies. ^[10] This leads to the fact that the same processes that occur in bodies, which are located in different 4-potentials, get out of phase. For the phase shift between two identical particles with the mass and the charge , one of which is in a certain gravitational (electromagnetic) field, we obtain:

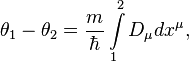
$~ \theta_1 -\theta_2 = \frac{m}{\hbar} \int\limits_{1}^{2} D_\mu dx^\mu ,$

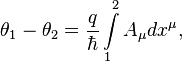
$~ \theta_1 -\theta_2 = \frac{q}{\hbar} \int\limits_{1}^{2} A_\mu dx^\mu ,$

here $~ \hbar$ is the Dirac constant, $~ A_\mu$ is the electromagnetic 4-potential, $~ dx^\mu$ is the 4-displacement of the particle in space and time.

The latter relation for the phase shift in electromagnetic field is confirmed by the Aharonov-Bohm effect.

The field energy theorem, which has the same meaning for fields as the virial theorem for particles, is applicable to a vector gravitational field in a curved spacetime. In the formulation of the theorem there is the gravitational 4-potential: ^[11]

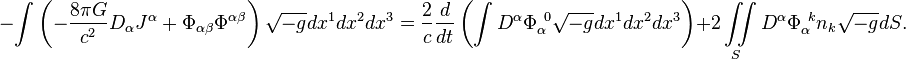
$~-\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {D^{\alpha }\Phi _{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{D^{\alpha }\Phi _{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.$

References

Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999. ISBN 5-8131-0012-1.
^2.0 ^2.1 ^2.2 ^2.3 Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
Fedosin S.G. Sovremennye problemy fiziki: v poiskakh novykh printsipov. Moskva: Editorial URSS, 2002, 192 pages. ISBN 5-8360-0435-8.
^4.0 ^4.1 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, no. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body. Preprints 2017, 2017040150. http://dx.doi.org/10.20944/preprints201704.0150.v1.
Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of Gravitomagnetic Theory. Canadian Journal of Physics, Vol. 92, No. 10, pp. 1074-1081 (2014). http://dx.doi.org/10.1139/cjp-2013-0683.
Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.
Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023.
Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.

External links

Gravitational four-potential in Russian

На русском языке