Gravitational torsion field

The gravitational torsion field is the force field acting on the masses and bodies in translational or rotational motion, which is the second component of the gravitational field in the Lorentz-invariant theory of gravitation and in the covariant theory of gravitation. By its action the torsion field is similar to the magnetic field in electromagnetism (see Maxwell-like gravitational equations). The term torsion field in this meaning was introduced by Sergey Fedosin in 1999. The torsion field dimension in the system of physical units SI is the same as for the frequency, that is s^-1.

Torsion field plays an important role in the gravitational model of strong interaction.

· 1 The torsion field in the Lorentz-invariant theory of gravitation

o 1.1 Heaviside's equations

o 1.2 The rotating particle in torsion field

o 1.3 Gravitational vector potential

· 2 The torsion field (gravitomagnetic field) in the general theory of relativity

· 3 The effects associated with the torsion field

· 4 The analogies with electrodynamics

· 5 See also

· 6 References

· 7 External links

The torsion field in the Lorentz-invariant theory of gravitation

In the Lorentz-invariant theory of gravitation (LITG) the force of gravitation is considered as the two-component force, which depends on the gravitational field strength (gravitational acceleration) $~ \mathbf{\Gamma }$ and the gravitational torsion field $~ \mathbf{\Omega}$ :

$~ \mathbf{F} = M \mathbf{\Gamma }+ M \left[\mathbf{v} \times \mathbf{\Omega} \right],$

where and $~\mathbf{v}$ are the mass and the velocity of the body moving in the gravitational field.

The torsion $~\mathbf{\Omega}$ in LITG up to a constant factor corresponds to the strength of the so-called gravitomagnetic field $~\mathbf{ H_g}$ in the general relativity (GTR). The cause of emergence of the torsion in LITG is the necessity to comply with the principle of Lorentz covariance for the gravitational field potentials in inertial reference frames. ^[1]

As the gravitational field strength, the torsion field contributes to the gravitational tensor, the gravitational stress-energy tensor, as well as the energy density of gravitational field:

$~u=-\frac{1}{8 \pi G }\left(\Gamma ^2+ c^2_{g} \Omega^2 \right),$

where $~ c_{g}$ is the speed of propagation of the gravitational influence or speed of gravity, is the gravitational constant,

the vector of energy flux density of gravitational field or Heaviside vector:

$~\mathbf{H} =-\frac{ c^2_{g} }{4 \pi G }[\mathbf{\Gamma }\times \mathbf{\Omega }],$

and Lagrangian for a particle in gravitational field.

Heaviside's equations

Torsion field is included in three of the four differential Heaviside's equations:

$~ \nabla \cdot \mathbf{\Omega}= 0,$

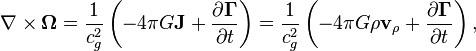
$~ \nabla \times \mathbf{\Omega}= \frac{1}{c^2_{g}} \left( -4 \pi G \mathbf{J} + \frac{\partial \mathbf{\Gamma }} {\partial t} \right) = \frac{1}{c^2_{g}} \left( -4 \pi G \rho \mathbf{ v_{\rho}} + \frac{\partial \mathbf{\Gamma }} {\partial t} \right),$

$~ \nabla \times \mathbf{\Gamma } = - \frac{\partial \mathbf{\Omega} } {\partial t},$

where:

· $~ \mathbf{J}$ is the mass current density,

· $~ \rho$ is the moving mass density,

· $~ \mathbf{ v_{\rho}}$ is the velocity of the mass flux, which creates the gravitational field and torsion.

From the first equation it follows, that the torsion field has no sources, and hence, the torsion field lines are always closed as in case of magnetic field. According to the second equation, the torsion is produced by the motion of matter and the change in time of gravitational field strength. The third equation implies effect of gravitational induction.

According LITG, the gravitational field strength $~ \mathbf {\Gamma}$ and torsion $~ \mathbf {\Omega}$ define the components of the real physical gravitational force, which can be substantiated at the quantum level like electromagnetic force. The torsion occurs whenever there is any movement of the mass. Since any motion can be divided into two parts – the rotational and translational, respectively, then we can talk about two kinds of torsion. Torsion outside the rotating sphere with angular momentum $~ \mathbf{L}$ has a dipole form: ^[2]

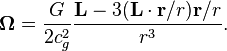
$~ \mathbf{\Omega}= \frac{G }{2 c^2_{g}} \frac{ \mathbf{L}- 3 (\mathbf{L} \cdot \mathbf{r} /r) \mathbf{r} /r}{r^3}.$

The presence of 1/2 in the formula for $~ \mathbf{\Omega}$ reflects the fact that the gravitational moment of the axisymmetric body is equal to the half of its angular momentum. In case of the rectilinear motion of the body, the torsion of gravitational field equals:

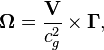
$~ \mathbf{\Omega}= \frac{ \mathbf{V}}{c^2_{g}} \times \mathbf{\Gamma },$

where $~\mathbf{V}$ is the velocity of the body, $~ \mathbf{\Gamma }$ is the gravitational field strength of the body at the point where the torsion $~ \mathbf{\Omega}$ is determined, and the strength $~ \mathbf{\Gamma }$ is taken in view of the propagation delay of the gravitational perturbation.

In the general case, the torsion from the arbitrarily moving point mass can be expressed through the gravitational field strength $~ \mathbf{\Gamma }$ produced by it:

$~ \mathbf{\Omega}= \frac{ 1 }{c_{g}} \mathbf{ e}_{r} \times \mathbf{\Gamma },$

where $\mathbf{ e}_{r}$ is the unit vector, directed from the point mass to the point where the torsion is determined, taken at earlier time taking into account the delay.

The rotating particle in torsion field

The formula for the moment of force acting on the rotating particle with the spin $~\mathbf{L}$ in torsion field $~ \mathbf{\Omega}$ , is written as follows:

$~ \mathbf{K} = \frac{1}{2} \mathbf{L} \times \mathbf{\Omega}.$

Since the particle is a top with the spin $~\mathbf{L}$ , then in the presence of the moment of forces $~ \mathbf{K}$ the particle would precess along the direction of the field $~ \mathbf{\Omega}$ . This follows from the equation of rotational motion:

$~ \mathbf{K} = \frac{d \mathbf{L} } {dt}.$

Since the moment of forces $~ \mathbf{K}$ is perpendicular to the spin $~ \mathbf{L}$ and the torsion $~ \mathbf{\Omega}$ , then the same is true for the increment of the spin $~d \mathbf{L}$ during the time . Perpendicularity of $~ \mathbf{L}$ and $~d \mathbf{L}$ leads to the precession of the spin of the particle at the angular velocity $~ \mathbf{w} = -\frac{ \mathbf{\Omega}}{2}$ around the direction of $~ \mathbf{\Omega}$ . The last equality follows from the fact that $~ \mathbf{K}= \frac{d \mathbf{L}} {dt}=\frac{1}{2} \mathbf{L} \times \mathbf{\Omega}$ , and the quantity $~w= \frac{dL} {L \sin Q dt} = \frac{d\varphi} {dt}$ , where is the angle between $~ \mathbf{\Omega}$ and $~ \mathbf{L}$ , and the increment of the angle $d\varphi$ is measured from the projection of the vector $\mathbf{L}$ on the plane perpendicular to the vector $~ \mathbf{\Omega}$ up to the projection of the vector $\mathbf{L}+ d \mathbf{L}$ on this plane.

In the presence of the non-uniform torsion field the particle with the spin $~ \mathbf{L}$ will be dragged to the region of the stronger field. From the equations of LITG the expression follows for such force:

$~ \mathbf{F} = \frac{1}{2}\nabla \left(\mathbf{L}\cdot \mathbf{\Omega} \right).$

The mechanical energy of the particle with the spin in the torsion field will be equal to:

$~U= -\frac{1}{2} \mathbf{L} \cdot \mathbf{\Omega}.$

Gravitational vector potential

Torsion field and gravitational field strength are closely related to the potentials of the field and expressed by the formulas:

$~\mathbf{\Omega }= \nabla \times \mathbf{D},$

$~\mathbf{\Gamma }= -\nabla \psi - \frac{\partial \mathbf{D}} {\partial t},$

where $~\psi$ is the scalar potential, $~ \mathbf{D}$ – the vector potential of the gravitational field.

The significance of potentials is in the fact that if a test particle of unit mass is placed in an external gravitational field, then $~\psi$ will set the additional energy of such particle due to action of the field, and $~ \mathbf{D}$ is a part of the generalized momentum of the particle.^[3] The vector potential of the field contributes to the torsion field and gravitational field strength, but the torsion field is not directly dependent on the scalar potential. When equations are wrote in four-dimensional form, field potentials form the gravitational four-potential $~ D_\mu$ , and the gravitational tensor, which consists of $~\mathbf{\Omega }$ and $~\mathbf{\Gamma },$ is obtained as the four-curl of $~ D_\mu$ .

The torsion field (gravitomagnetic field) in the general theory of relativity

In contrast to Newtonian mechanics, in the general theory of relativity (GTR), the motion of the test particle (and the rate of clock) in the gravitational field depends on whether the body, the source of the field, rotates or not. The influence of rotation affects even in the case when the distribution of masses in the source in its reference frame does not change with time (for example, there is cylindrical symmetry with respect to the axis of rotation). Gravitomagnetic effects in weak fields are extremely small. In the weak gravitational field and at low velocities of the particles we can consider separately the gravitomagnetic and the gravitational forces acting on the test body, and the strength of the gravitomagnetic field and the gravitomagnetic force are described by the equations similar in the form to the corresponding equations of electromagnetism.

We shall consider the motion of the test particle in the vicinity of the rotating spherically symmetric body with the mass and the angular momentum $~ \mathbf{L}$ . If the particle with the mass is moving at the velocity $~v\ll c$ ( is the speed of light), then the particle would be influenced, in addition to the gravitational force, by the gravitomagnetic force, directed (like the Lorentz force) perpendicular to both the velocity and the strength of the gravitomagnetic field $~ \mathbf{ H_g }$ . In the CGS system of physical units we shall have:

$~ \mathbf{F}= \frac{m}{c} \left[\mathbf{v} \times 2 \mathbf{ H_g } \right].$

And if the rotating mass is located at the origin of coordinates and $~ \mathbf{r}$ is the radius vector to the observation point, the strength of the gravitomagnetic field at this point is: ^[4]

$~ \mathbf{ H_g }= \frac{G }{c} \frac{ \mathbf{L} - 3(\mathbf{L} \cdot \mathbf{r}/r) \mathbf{r}/r}{r^3},$

where is the gravitational constant.

The last formula coincides (except for the coefficient) with the similar formula for the field of the magnetic dipole with the magnetic dipole moment equal to $~ \mathbf{L}$ . In GTR gravitation is not an independent physical force. Gravitation in GTR is rather reduced to the curvature of spacetime and is treated as a geometric effect, and is equated to the metric field. ^[5][6] The same geometric meaning is obtained by the gravitomagnetic field $~\mathbf{ H_g }$ .

In contrast to this, in LITG it is assumed that the force of torsion arises already in the Minkowski space, as a magnetic force. In GTR the equivalent gravitomagnetic force is considered in the Riemannian space, where gravitation has tensor, not vector character. Therefore, the spin of gravitons in GTR is assumed twice greater than in the vector theory of LITG. Hence, in a number of works on gravitoelectromagnetism in GTR, in the expressions for the force and the gravitomagnetic field the additional numerical factors appear in comparison with the expressions for the force and the torsion field in LITG. For rectilinear motion of bodies the formulas for the torsion in LITG and in GTR coincide. ^[7]

The effects associated with the torsion field

In the case of strong fields and relativistic velocities the torsion field can not be considered separately from the gravitational field, since the dependence of the metric tensor on the value of the fields is beginning to affect, and the field equations become interrelated and nonlinear. In this case LITG turns into the covariant theory of gravitation (CTG). ^[8] In weak fields as separate effects of the torsion field the following effects are considered:

· Dragging of inertial reference frames. This is precession of the spin and orbital moments of the test particle near the rotating massive body. In the SI system of physical units the angular velocity of precession is equal to $~ \mathbf{w}= -\frac{\mathbf{\Omega}}{2}$ and is directed against the direction of torsion field $~ \mathbf{\Omega}$ .

· The orbital Lense-Thirring effect, which leads to precession, that is to the rotation of the normal of the elliptical orbit of the particle relative to the vector of gravitational torsion field of the rotating body. This effect is vectorially added to the standard general relativistic precession of the pericenter (43" per century for Mercury), which does not depend on the rotation of the central body. The orbital Lense-Thirring precession was first measured for the satellites LAGEOS and LAGEOS II.

· The spin Lense-Thirring effect (or the Schiff precession) is expressed in the precession of gyroscope, located near the rotating body. If we consider the gyroscope as a spinning top, then the axis of this top will periodically change its direction in space with the precession frequency. Checking this precession was one of the goals of the experiment of Gravity Probe B, conducted by NASA in 2005-2007 on the satellite with the orbit passing through the pole of the Earth. ^[9] However, the measurement errors were too large, in the range of 256-128%, impeding the measurements. ^[10]The experimental measurement of the Schiff precession is the test for the theories of GTR and CTG with respect to the formulas for the precession. At the Earth’s pole the angular velocity of precession is directed similarly to the spin of the Earth , and from CTG it follows:

$~w = -\frac{\Omega }{2}= \frac{G L}{2 c^2_{g} r^3},$

where is the distance from the Earth’s center to the gyroscope in the orbit near the pole.

Measuring allows direct determination of the speed of gravitation propagation $~c_{g}$ in CTG. The same formula for angular velocity of precession is valid in general relativity, but averaged over the whole orbit. ^[11] With $~ c_{g}=c$ for the we must have the value 0.0409 arc seconds per year (here km for the satellite Gravity Probe B, is the Earth's radius, the altitude of the satellite is 640 km).

· The geodetic precession (de Sitter effect) occurs in parallel transfer of the angular momentum vector in the curved spacetime. For the Earth-Moon system, moving in the field of the Sun, the geodetic precession is 1.9" per century; the precise astrometric measurements revealed this effect, which coincided with the predicted within the error range of 1 %. The geodetic precession of gyroscopes on the satellite Gravity Probe B coincided with the predicted value (the rotation of the axis by 6.606 arc seconds per year in the plane of the satellite’s orbit) with the accuracy more than 1 %. The formula for the de Sitter precession in GTR has the form: ^[12]

$~ \mathbf{w} = \frac{3}{2} \frac{G M}{c^2 r^3} \mathbf{r} \times \mathbf{V} =\frac{3}{2} \frac{G M}{c^2 r^2} \mathbf{\omega}_o,$

where $~ \mathbf{V}$ is the velocity of motion of the gyroscope in the orbit of the Earth, is the mass of the Earth, $~ \mathbf{\omega}_o$ is the orbital angular velocity of the gyroscope’s rotation.

The angular velocity of the geodetic precession is perpendicular to the velocity of the gyroscope and to the acceleration of Earth's gravitation, coinciding with the direction of the orbital angular velocity of rotation. Therefore, at the pole of the Earth the geodetic precession is perpendicular to the spin precession in the Schiff effect, the angular velocity of which is directed along the axis of the Earth’s rotation.

· The gravitomagnetic time shift. In the weak fields (for example, near the Earth) this effect is masked by the standard special and general relativistic effects of the change of the rate of clock and is far beyond the current accuracy of the experiment.

The analogies with electrodynamics

Since the gravitational torsion field is similar to the magnetic field in electrodynamics, and the angular momentum of the particle is similar to the dipole magnetic moment, then according to LITG it allows us to interpret the Lense-Thirring effect at the example of rotation of the electrically charged test particle around the body attracting it, if this body has the dipole magnetic moment. Due to the law of conservation of the orbital angular momentum, the orbital plane of the particle tends not to change its position in space. However, during the rotation of the particle around the body, the charge of the particle will be influenced by the additional Lorentz force from the magnetic field of the body, which is perpendicular to the particle velocity. In the stationary state, the velocity and the orbital angular momentum of the particle will not change in the magnitude, but the orbit of the rotating particle and the direction of its orbital angular momentum will precess relative to the axis of the dipole magnetic moment of the body, as in the orbital Lense-Thirring effect.

If the particle has its proper magnetic moment and spin, then there will be interaction of the magnetic moments of the particle and the body. The energy of this interaction depends on the mutual orientation of the magnetic moments. The magnetic field of the body will tend to establish the magnetic moment of the particle in the direction of the field, but the particle has the spin, tending to preserve its direction in space. Therefore there will be precession of the particle’s spin relative to the axis of the dipole magnetic moment of the body, similar to the Schiff effect.

Another effect is associated with the orbital motion of the particle with the magnetic moment and spin relative to the charged body. In the rest frame of the center of mass of the particle, the particle itself is rotating, and the body is rotating around this particle. The orbital rotation of the charged body creates the magnetic field acting on the magnetic moment of the particle. This leads to the precession of the magnetic moment and the spin of the particle relative to the magnetic field from the orbital rotation of the body. Now we shall replace the magnetic field by the torsion of the gravitational field, and the charges by masses. Then it turns out that the angular velocity of the spin precession of the particle would be one third of the angular velocity of the geodetic precession (the other two thirds arise from the curvature of the spacetime around the body due to changing of the metric).

References

1. Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron, 2007, Vol. 14, No. 4, P. 385 – 413.

2. Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999. ISBN 5-8131-0012-1.

3. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75. http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023 .

4. L. Iorio, H.I.M. Lichtenegger, M.L. Ruggiero, C. Corda. Phenomenology of the Lense-Thirring effect in the Solar System. arXiv:1009.3225v2 16 Sep 2010.

5. Professor R.W. Tucker Publications. Can one measure Spacetime Torsion?, Proceedings for 60th birthday tribute to J. Azcaragga, Salamanca, Spain, June 2003.

6. H. I. Arcos and J. G. Pereira. Torsion and the gravitational interaction. arXiv:gr-qc/0408096 v2 4 Nov 2004.

7. Sergei M. Kopeikin. Gravitomagnetism and the Speed of Gravity. Int. J. Mod. Phys.D 15:305-320, 2006.

8. Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).

9. Everitt, C.W.F., et al., Gravity Probe B: Countdown to Launch. In: Laemmerzahl, C., Everitt, C.W.F., Hehl, F.W. (Eds.), Gyros, Clocks, Interferometers…: Testing Relativistic Gravity in Space. — Berlin, Springer, 2001, pp. 52-82.

10. Muhlfelder, B., Mac Keiser, G., and Turneaure, J., Gravity Probe B Experiment Error, poster L1.00027 presented at the American Physical Society (APS) meeting in Jacksonville, Florida, on 14-17 April 2007, 2007.

11. Yi Mao , Max Tegmark, Alan Guth, Serkan Cabi. Constraining Torsion with Gravity Probe B. arXiv:gr-qc/0608121v45, Phys. Rev. D. 76, 104029, 2007.

12. N. Straumann, General Relativity and relativistic Astrophysics, Springer-Verlag, Berlin, Heidelberg, New York, 1991.

External links

In Search of gravitomagnetism, NASA, 20 April 2004.
Gravitomagnetic London Moment-New test of General Relativity?
Measurement of Gravitomagnetic and Acceleration Fields Around Rotating Superconductors M. Tajmar, et. al., 17 October 2006.
Gravitational torsion field in Russian

На русском языке