Gravitational constant

Gravitational constant

The gravitational constant $~G\;$ is a fundamental physical constant, a gravitational interaction constant.

The gravitational constant G is a key quantity in Newton's law of universal gravitation.

Contents

1 Introduction
2 The history of measurement
3 Theoretical definition
4 References
5 See also
6 External links

Introduction

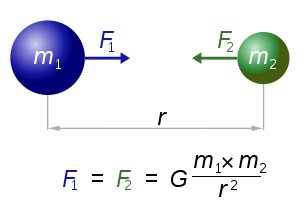
According to the Newton's law of universal gravitation, the force of gravitational attraction between two material points with gravitational masses m₁ and m₂, which are located at the distance R, is equal to:

$F=G{\frac {m_{1}m_{2}}{R^{2}}}.$

The proportionality coefficient G in this equation is called the gravitational constant. Numerically it is equal to the absolute value of the gravitational force, acting on a point body with unit mass from another similar body, which is located at the unit distance.

In SI units the value recommended for the year 2014 is: ^[1] $G=6.67408(31)\cdot 10^{{-11}}$ m³·s⁻²·kg⁻¹, or N·м²· kg⁻².

The gravitational constant is presented in most of the formulas associated with the gravitational interaction. In particular, it is included in the equations of the general relativity, the gravitoelectromagnetism and the covariant theory of gravitation, and it is also part of the formulas used to determine the gravitational torsion field. The gravitational constant and its coupling constant have such values that the gravitational interaction between the elementary particles is many orders of magnitude less than the weak, electromagnetic, and strong interactions.

In the theory of Infinite Hierarchical Nesting of Matter, based on the SPФ symmetry the existence of strong gravitation is assumed, which is acting on the level of elementary particles. The strong gravitational constant is derived from the ordinary gravitational constant by multiplying it by the similarity coefficients, which are found on the basis of similarity of matter levels.

The history of measurement

The gravitational constant is used in the modern law of universal gravitation, but it was not used in Newton’s works and in the works of other scientists until the beginning of the 19^thcentury. The gravitational constant apparently was first introduced into the law of universal gravitation only after transition to the single metric system of measurements. Possibly it was first done by the French physicist Poisson in “Treatise on Mechanics” (1809) — at least historians have not found any earlier works, in which the gravitational constant was mentioned. In 1798 Henry Cavendish prepared and performed the Cavendish experiment to determine the average density of the Earth using the torsion balance, invented by John Michell (Philosophical Transactions 1798). Cavendish compared the pendular oscillations of the test body under the action of gravitation of the balls with known mass and under the action of the Earth's gravitation. The numerical value of the gravitational constant was calculated later based on the average density of the Earth and resulted in the value $G=6.754\cdot 10^{{-11}}$ m³·s⁻²·kg⁻¹. ^[2]

The accuracy of the measured value of G since the time of Cavendish’s experiment increased insignificantly.

Theoretical definition

In order to calculate the gravitational constant Maurizio Michelini used the idea of micro-quanta, filling the entire space, interacting with the bodies’ particles and as a result pushing the bodies to each other. ^[3] For the matter consisting mainly of nucleons he obtains the following:

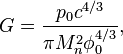
$~G={\frac {p_{0}c^{{4/3}}}{\pi M_{n}^{2}\phi _{0}^{{4/3}}}},$

where $~p_{0}=4.33\cdot 10^{{61}}$ J/m³ is the energy density of the fluxes of micro-quanta; $~M_{n}$ is the nucleon mass; is the speed of light; $~\phi _{0}=1.35\cdot 10^{{102}}$ m⁻²•s⁻¹ is the fluence rate of the fluxes of micro-quanta in one direction.

Sergey Fedosin expressed the gravitational constant in the framework of Le Sage’s theory of gravitation in terms of the parameters describing the vacuum field of gravitons. ^[4] ^[5] ^[6] In the model of cubic distribution of graviton fluxes:

$~G={\frac {3p_{g}D_{0}\sigma ^{2}}{2\pi M_{n}^{2}}}={\frac {\varepsilon _{c}\sigma ^{2}}{4\pi M_{n}^{2}}}.$

Here $~p_{g}$ is the momentum of gravitons interacting with the nucleon matter; the fluence rate $~D_{0}$ denotes the number of gravitons dN, that during the time dt fell to the area dA (perpendicular to the flux) of one face of a certain cube, which limits the volume under consideration; $~\sigma =5.6\cdot 10^{{-50}}$ m² is the cross-section of interaction of gravitons and nucleons; $~M_{n}$ is the nucleon mass; $~\varepsilon _{c}=7.4\cdot 10^{{35}}$ J/m³ is the energy density of the graviton fluxes for cubic distribution.

In the model of spherical distribution of graviton fluxes:

$~G={\frac {4p_{g}B_{0}\sigma ^{2}}{M_{n}^{2}}}={\frac {\varepsilon _{s}\sigma ^{2}}{6\pi M_{n}^{2}}},$

where the fluence rate $~B_{0}$ denotes the number of gravitons dN, that during the time dt fell from the unit solid angle $d{\alpha }$ inside the spherical surface dA; $~\varepsilon _{s}=1.1\cdot 10^{{36}}$ J/m³ is the energy density of the graviton fluxes for spherical distribution.

Since the gravitational constant is expressed in terms of other variables, it is a dynamic variable, which is constant only on the average.

The interaction cross-section $~\sigma$ can be expressed in terms of the cross-section $~\vartheta =2.67\cdot 10^{{-30}}$ m² of interaction of the charged particles of the vacuum field (praons) with nucleons: ^[6]

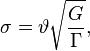
$~\sigma =\vartheta {\sqrt {{\frac {G}{\Gamma }}}},$

where $\Gamma$ is the strong gravitational constant. The interaction cross-section $~\vartheta$ is very close in magnitude to the geometrical cross-section of the nucleon and is used to calculate the electric constant. If we substitute the expression of $~\sigma$ in terms of $~\vartheta$ into the formula for the gravitational constant in the cubic distribution model, we will obtain a relationship between the strong gravitational constant, the nucleon’s parameters and the energy density of the graviton fluxes at the nucleon level of matter:

$~\Gamma ={\frac {\varepsilon _{c}\vartheta ^{2}}{4\pi M_{n}^{2}}}.$

Similarly, for the gravitational constant at the stellar level of matter, there is a relationship between the corresponding energy density of the graviton fluxes and the parameters of the neutron star, which is an analogue of the nucleon:

$~G={\frac {\varepsilon _{{cs}}\vartheta _{s}^{2}}{4\pi M_{s}^{2}}},$

where $\varepsilon _{{cs}}=\varepsilon _{c}{\frac {\Phi 'S'^{2}}{P'^{3}}}=2.3\cdot 10^{{34}}$ J/m³ is the energy density of the graviton fluxes at the stellar level for cubic distribution; $~\vartheta _{s}=\vartheta P'^{2}=5.2\cdot 10^{{8}}$ m² is the cross-section of interaction between the gravitons and the neutron star; $~M_{s}=M_{n}\Phi '=2.7\cdot 10^{{30}}$ kg is the neutron star’s mass. In the calculation we used the similarity coefficients according to the similarity of matter levels: $~\Phi '=1.62\cdot 10^{{57}}$ is the coefficient of similarity in mass, $~P'=1.4\cdot 10^{{19}}$ is the coefficient of similarity in sizes, is the coefficient of similarity in speeds of same-type processes.

Thus, it is assumed that at each level of matter there is its own gravitational constant, besides the energy density of the corresponding graviton fluxes increases with the transition to the lower levels of matter.

The quantity $\varepsilon _{{cs}}$ can be compared with the energy density of the gravitational wave in the GW150914 event. It is assumed that this event was caused by a merger of two black holes with masses of 30 and 35 solar masses, rotating near each other under the action of gravitation, during decrease in the distance between them up to 350 km, while the maximum power of gravitational radiation reached $3.6\cdot 10^{{49}}$ W. ^[7] If we divide this power by the surface of the sphere with the radius of 175 km, we will obtain an estimate of the density of the energy flux passing through the surface of the sphere. Then this value can be divided by the speed of light, and we can estimate the energy density in the wave: $\approx 10^{{30}}$ J/m³. The energy density of the wave is found to be substantially lower than the energy density of the gravitons’ vacuum field. Thus, the gravitational wave from the majority of powerful radiation sources only slightly modulates the graviton fluxes in the cosmic space.

References

Newtonian constant of gravitation G. CODATA, NIST.
Brush, Stephen G.; Holton, Gerald James (2001), Physics, the human adventure: from Copernicus to Einstein and beyond, New Brunswick, N.J: Rutgers University Press, p. 137, ISBN 0-8135-2908-5.
Maurizio Michelini. Discussion on Fundamental Problems of Physics Hidden in Cosmology. Applied Physics Research. Vol. 8, No. 5. pp.19-43 (2016). http://dx.doi.org/10.5539/apr.v8n5p19.
Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
Fedosin S.G. The Force Vacuum Field as an Alternative to the Ether and Quantum Vacuum. WSEAS Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN: 1991-8747 / 2224-3429, Volume 10, Art. #3, pp. 31-38 (2015).
^6.0 ^6.1 Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.
Abbott, B. P.; et al. (LIGO Scientific Collaboration, Virgo Collaboration), Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 116, 061102 (2016). https://dx.doi.org/10.1103/PhysRevLett.116.061102.

See also

External links

Source: http://sergf.ru/gpoen.htm

On the list of pages