На русском языке

Coupling constant

Coupling constant (or interaction constant) is a parameter in field theory, which determines relative strength of interaction between particles and fields. In quantum field theory coupling constants are associated with vertices of corresponding Feynman diagrams. Dimensionless parameters are used as coupling constants, as well as quantities associated with them that characterize interaction and have dimensions. Examples are dimensionless fine structure constant of electromagnetic interaction and the electric elementary charge, measured in coulombs (C).

Contents

  • 1 Comparison of interactions
    • 1.1 Gravitational interaction
    • 1.2 Weak interaction
    • 1.3 Electromagnetic interaction
    • 1.4 Strong interaction
  • 2 Constants in quantum field theory
  • 3 Constants in other theories
    • 3.1 String theory
    • 3.2 Strong gravitation
    • 3.3 Interactions at level of stars
  • 4 References
  • 5 See also
  • 6 Additional references
  • 7 External links

Comparison of interactions

For a physical system that participates in all four fundamental interactions, values of dimensionless interaction constants, found by general rule, show relative strength of these interactions. The proton is most often used as such a physical system at the level of elementary particles. The basic energy for comparison of interactions is electromagnetic energy of a photon, which equals by definition:

U_f= \frac{h c}{\lambda},

where ~h   is Planck constant, ~c   is speed of light, ~\lambda   is photon wavelength. The choice of photon energy is not accidental, since basis of modern science is wave representation based on electromagnetic waves. All main measurements, including length, time and energy, are made with the help of them.

Gravitational interaction

Energy of gravitational interaction between two protons is given by:

U_{g}= -\frac{G M^2_p}{r},

where ~G   is gravitational constant, ~M_p   is proton mass, ~r   is distance between the protons’ centers.

If we assume that distance ~r   and electromagnetic photon’s wavelength ~\lambda   are related by the formula ~\lambda =2 \pi r , then ratio of absolute value of gravitational interaction energy to photon’s energy gives dimensionless coupling constant:

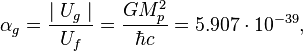
\alpha_{g}=\frac {\mid U_{g}\mid }{ U_f } = \frac{G M^2_p }{\hbar c }=5{.}907\cdot10^{-39},

where ~\hbar   is Dirac constant.

Weak interaction

Energy associated with weak interaction can be represented as follows:

U_{W}= \frac{g^2_F}{4 \pi r} \exp (-\frac {M_W cr}{\hbar }),

where ~g_F   is effective charge of weak interaction, ~M_W   is mass of virtual particles that are considered carrier particles for weak interaction (W and Z bosons). Square of effective charge of weak interaction for proton is expressed in terms of Fermi constant  ~G_F=1.43 \cdot 10^{-62}  J•m3 and proton mass:

g^2_{F}= \frac{4 \pi G_F M^2_p c^2}{\hbar^2 }.

At sufficiently small distances exponent in weak interaction energy can be neglected. In this case, dimensionless coupling constant of weak interaction is determined as follows:

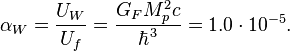
\alpha_{W}=\frac { U_{W}}{ U_f } = \frac{G_F M^2_p c }{\hbar^3 }=1{.}0\cdot10^{-5}.

Electromagnetic interaction

Electromagnetic interaction of two fixed protons is described by electrostatic energy:

U_{e}=\frac{e^2}{4\pi \varepsilon_0 r},

where ~e   is elementary charge, ~\varepsilon_0   is electric constant.

Ratio of this energy to photon energy ~U_f  determines electromagnetic coupling constant, known as fine structure constant:

\alpha=\frac { U_{e}}{ U_f } =\frac{e^2}{4\pi\varepsilon_0 \hbar c}=7{.}297\cdot10^{-3}.

Strong interaction

At the level of hadrons, strong interaction is regarded in Standard Model of elementary particle physics as “residual” interaction of quarks that are part of hadrons. It is assumed that gluons as carriers of strong interaction generate virtual mesons in space between hadrons. In pion-nucleon model of Yukawa interaction, nuclear forces between nucleons are explained as a result of virtual pions exchange, and interaction energy is as follows:

U_{s}=- \frac{g^2_{N \pi}}{4 \pi r} \exp (-\frac {M_{\pi} cr}{\hbar }),

where ~g_{N \pi}   is effective charge of pseudoscalar pion-nucleon interaction, ~ M_{\pi}   is pion mass.

Dimensionless strong interaction coupling constant is:

\alpha_{s}=\frac { \mid U_{s}\mid }{ U_f } = \frac{ g^2_{N \pi}}{4\pi\hbar c } \approx 14{.}6.

Constants in quantum field theory

Interaction effects in field theory are often determined with the help of perturbation theory, in which expansion of functions in equations in powers of coupling constant is performed. Usually for all interactions, except strong interaction, coupling constant is significantly less than unity. This makes the use of perturbation theory effective, since contribution from highest terms of expansions decreases rapidly and calculating them becomes unnecessary. In case of strong interaction the perturbation theory becomes unsuitable and other methods of calculation are required.

One of predictions of quantum field theory is the so-called effect of “floating constants”, according to which coupling constants change slowly with increasing of energy, transferred during interaction between particles. Thus, electromagnetic coupling constant increases and strong interaction constant coupling decreases with increase of energy. In Quantum Chromodynamics a special strong interaction coupling constant is introduced for quarks:

\alpha_{sq}= \frac{ g^2_{qg}}{4\pi\hbar c } <1,

where ~g_{ qg }   is effective color charge of a quark, emitting virtual gluons for interaction with other quarks.

As distance between quarks decreases, due to collisions of high energy particles, logarithmic decrease of  ~\alpha_{sq} and weakening of strong interaction (effect of asymptotic freedom of quarks) are expected. [1] At the scale of transferred energy of the order of Z boson’s mass-energy (91.19 GeV) it was found that  ~\alpha_{sq}=0.1187. [2] At the same energy scale electromagnetic interaction coupling constant increases up to value of the order of 1/127 instead of ≈1/137 at low energies. It is assumed that at higher energies, of the order of 1018 GeV, values of coupling constants of gravitational, weak, electromagnetic and strong interactions of particles will become closer and even become approximately equal to each other.

Constants in other theories

String theory

In string theory, coupling constants are considered not as constant but as dynamic quantities. In particular, at low energies it seems that strings move in ten dimensions and at high energies — in eleven dimensions. The changing number of dimensions is accompanied by a change in coupling constants. [3]

Strong gravitation

Strong gravitation together with gravitational torsion field and electromagnetic forces are considered main components of strong interaction in gravitational model of strong interaction. In this model, instead of considering interactions of quarks and gluons, only two fundamental fields (gravitational and electromagnetic fields) are taken into account, which act in charged matter of elementary particles that has mass, as well as in space between them. In this case, quarks and gluons, according to model of quark quasiparticles, are considered not as real particles but as quasiparticles, reflecting quantum properties and symmetry, inherent in hadronic matter. This approach dramatically reduces number of actually unsubstantiated but postulated free parameters in standard model of particle physics, which has at least 19 such parameters, which is a record for physical theories.

Another consequence is that weak and strong interactions are not considered as independent field interactions. Strong interaction is reduced to combinations of gravitational and electromagnetic forces, in which an important role is played by interactions’ delay effects (dipole and orbital torsion fields and magnetic forces). Accordingly, strong coupling constant is determined by analogy with gravitational interaction coupling constant: [4]

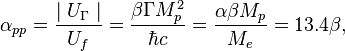
\alpha_{pp}=\frac {\mid U_{\Gamma}\mid }{ U_f } = \frac{\beta \Gamma M^2_p }{\hbar c }=\frac { \alpha \beta M_p }{ M_e }=13{.}4 \beta ,

where ~\Gamma   is strong gravitational constant, ~ M_e   is electron mass, ~\beta   is a coefficient, which is equal to 0.26 for interaction of two nucleons and is tending to 1 for bodies with lower matter density.

As for weak interaction, it is assumed to be a result of transformation of matter of elementary particles, which occurs due to reactions of weak interaction, but at a deeper level of matter. Examples of weak interaction with nucleons are considered in substantial neutron model and substantial proton model.

Interactions at level of stars

Among stellar constants, describing quantization of parameters of cosmic systems in hydrogen system of stars, there are two dimensionless constants. One of them determines stellar fine structure constant ~\alphaand the other determines relative strength of interaction between two stars. In case of hydrogen system of a magnetar and a disks near it these constants equal:

~\alpha= \frac { Q^2_s }{4 \pi \varepsilon_0 \hbar'_s C'_s }= \frac { G M_s M_d }{ \hbar'_s C'_s }= 7.2973525376 \cdot 10^{-3},

 

~\alpha_{mm}= \frac { \beta Q^2_s M_s }{4 \pi \varepsilon_0 M_d \hbar'_s C'_s }= \frac{\beta G M^2_s }{\hbar'_s C'_s }=\frac { \alpha \beta M_s }{ M_d }=13{.}4 \beta , 

where  ~ Q_s = 5.5 \cdot 10^{18} C is electric charge of magnetar, based on its similarity with proton, ~\hbar'_s= 5.5 \cdot 10^{41}  J∙s is the stellar Dirac constant for system with magnetar, ~ C'_s= 6.8 \cdot 10^{7} m/s is e stellar speed as characteristic speed of matter particles in a typical neutron star, ~M_{s}= 1.35 M_c=2.7\cdot 10^{30} kg is the mass of the magnetar, ~ M_d= 1.5 \cdot 10^{27} kg is mass of disk, which is electron’s analogue at the level of stars.

Due to SPФ symmetry and similarity of matter levels, values of dimensionless coupling constants are the same both at the atomic level and at the level of stars.

References

  1. Wilczek, F.; Gross, D.J. (1973). "Asymptotically Free Gauge Theories". Phys. Rev. D 8 (10): 3633. doi:10.1103/PhysRevD.8.3633.
  2. Yao W-M et al. (Particle Data Group) J. Phys. G: Nucl. Part. Phys. Vol. 33, P. 1 (2006).
  3. Гросс, Дэвид. Грядущие революции в фундаментальной физике. Проект «Элементы», вторые публичные лекции по физике (25.04.2006).
  4. Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).

See also

Additional references

  • Р. Маршак, Э. Судершан. Введение в физику элементарных частиц, 1962.
  • M.E. Peskin and H.D. Schroeder. An introduction to quantum field theory, ISBN 0-201-50397-2.

External links

 

Source: http://sergf.ru/kven.htm

On the list of pages