Discreteness of stellar parameters

Discreteness of stellar parameters is the property of distribution of the observed stars, in which the values of some of their parameters are preferred and are more common than others.

From the physical point of view, the cause of the discreteness of stellar parameters is the discreteness associated with the equations of the state of the stellar matter and with the phase transitions in this matter. This discreteness leads to dividing all stars into different types, such as main-sequence stars, subdwarfs, giants, supergiants, white dwarfs and neutron stars. For main-sequence stars primary discreteness is also important, arising from different masses, angular momenta and the temperature of the gas clouds, which form the stars.

The idea of discreteness of stellar parameters conforms to the Theory of Infinite Hierarchical Nesting of Matter, the similarity of matter levels and the quantization of parameters of cosmic systems. This is due to the fact that planetary systems of stars are in many aspects similar to atoms, and at the atomic matter level the masses of atoms are discrete as well as their other parameters, including the electric charge and the magnetic moment. The similarity between the atoms and the stars leads to significant peculiarities of the description of discreteness of stellar parameters, which specify our understanding of the evolution of cosmic objects under the influence of the fundamental forces.

1 The model of R. Oldershaw
2 The model of S. Fedosin

2.1 The Solar system
2.2 Ordinary stars

2.2.1 The characteristics
2.2.2 The correspondence between the atoms and the stars
2.2.3 Abundance of stars of different spectral types
2.2.4 Binary and multiple stars
2.2.5 Characteristic speeds
2.2.6 The angular momenta
2.2.7 The magnetism of stars

2.3 Compact stars

3 References
4 See also
5 External links

The model of R. Oldershaw

Robert L. Oldershaw since the 70's has been studying the hierarchical structure of the Universe and the discreteness of the parameters of its objects. The relations between the sizes, the durations of processes and the masses of similar objects in his model are as follows: ^[1]

$R_N= \Lambda R_{N-1}, \qquad\qquad T_N = \Lambda T_{N-1}, \qquad\qquad M_N =X M_{N-1},$

where N is the number of the matter level, for example, the level of stars; N-1 is the number of the lower level of matter, for example, the atomic level of matter; $\Lambda$ and are dimensionless coefficients, which are subject to be determined.

In the assumption that the Universe is fractal and consists of self-similar objects, the following formula is used: ^[2]

$n_o = (\frac {R_N}{R_{N-1}})^D,$

where is the number of objects at the N-1 level, which are part of the N level; is the similarity constant or the fractal dimension.

If we assume that $n_o = \frac {M_N}{M_{N-1}} = X$ , then it follows that $~M_N =\Lambda^D M_{N-1}$ .

Finding the similarity between the atoms and the stars, Oldershaw faced the question – to which atom does the Solar System correspond? As a first approximation, he considers Jupiter and the Sun as some analogue of the hydrogen atom. For the radius of the orbit and the velocity of the electron in the hydrogen atom in the Bohr theory there are the following relations:

$r = n^2 a_0 , \qquad\qquad v = \frac {v_0}{n},$

where is the principal quantum number, is the Bohr radius, is the electron’s velocity on the Bohr radius with .

In the Oldershaw model the velocities of similar objects, defined as the changes of the corresponding distances per relevant time unit, have the similarity coefficient equal to unity. This follows from the fact that in the transition from the lowest level of matter to a higher level, the distances and the time intervals are multiplied by the same coefficient $\Lambda$ , and the velocities remain the same. Hence, for the orbital radius a.u. and the velocity km/s of Jupiter we must have:

$R_J = n^2 a_0 \Lambda, \qquad\qquad V_J = \frac {v_0}{n}.$

$n \approx 168, \qquad\qquad \Lambda \approx 5.2 \cdot 10^{17}.$

Based on the large value $n \approx 168$ , the Solar system is assumed to be similar to the Rydberg atom. Although Oldershaw determines $\Lambda$ by comparing the Solar system and the hydrogen atom, but to determine the coefficient of similarity in mass, he does not compare the masses of the Sun and of the nucleus of the hydrogen atom (or the masses of Jupiter and of the electron). Instead, he believes that often observed stars of the spectral type M, with the mass of about (where is the mass of the Sun) are the stellar analogue of the hydrogen atom, with the mass . Then, the coefficient of similarity in mass is equal to $X=\Lambda^D =\frac {0.145 M_c }{M_p}=1.73 \cdot 10^{56}$ , .

As an additional argument in favor of such determination is the fact that the planetary nebula with the white dwarfs located in them with typical masses are associated as the stellar analogues of the positive helium ion, which contains four nucleons. With this approach, the stars of the spectral type K are similar to the helium nuclei, and the Sun must be the analogue of the nuclide, containing 7 nucleons, like lithium. More massive main-sequence stars, giants and supergiants are considered as the stellar analogues of the Rydberg atoms and ions. Since the matter of the electron, bound in the atom, is assumed to be somehow distributed over the volume of the atom, the matter of the stellar analogue of the electron in planetary systems can be in the form of the spherical shell of the star with small , or can be in the form of planets with large . Using the radii of the atoms and ions in ordinary and up to the most highly excited Rydberg states, and multiplying these radii by $\Lambda$ , Oldershaw simulates the observed radii of the main-sequence stars, giants and supergiants. Table 1 shows the masses of the stars of the lower part of the main sequence, which are expected in the Oldershaw model.

Table 1. The expected discreteness of the stellar masses
Atoms / Isotopes	Number of nucleons, N	The atomic mass, Da	The predicted mass of the stars, $M_{c}$
H¹	1	1.008	0.146
H²	2	2.014	0.292
He³, (H³)	3	3.016	0.437
He⁴	4	4.003	0.580
Stable nuclei with 5 nucleons are absent	–	The "gap" in the distribution of the nuclear masses	The "gap" in the distribution of stellar masses with 0.73 $M_{c}$
Li⁶, (He⁶)	6	6.015	0.872
Li⁷, (Be⁷)	7	7.016	1.017
Li⁸, (Be⁸, B⁸)	8	8.005	1.160
Be⁹, (Li⁹)	9	9.012	1.306

Oldershaw also compares the variable stars with the Rydberg atoms. In particular, the stars of the type RR Lyrae are considered to be the analogues of the neutral helium atom, in which there are transitions of electrons between the states with the principal quantum number from 7 to 9. ^[3] In the Rydberg atoms for the motion of the electron, like in the planetary systems for the motion of planets, the relation holds between the square of the orbital period of rotation and the cube of the orbit’s radius: . Oldershaw transfers this relation to the different types of variable stars, recalculating the coefficients into the coefficients for the level of stars by multiplying by $\Lambda$ . Thus he connects the oscillation periods of the brightness of variable stars with their radii.

Until 1985 Oldershaw believed that the objects of any level of matter are composed mostly of the objects of the lower level of matter with almost no changes in their state. Then he changed his opinion, attributing to the black holes the dominant role in the cosmological hierarchy. In this case, the objects of the lower levels of matter form the observed mass, but these objects change dramatically in the singularities of black holes. From the coefficients of similarity in size and time obtained by Oldershaw $\Lambda \approx 5.2 \cdot 10^{17}$ , it follows that the radius of the star, the analogue of the proton, can be obtained by multiplying the radius of the proton by $\Lambda$ . This gives approximately the same radius, which the star would have with the mass , if it were a black hole:

$R = \frac {2 G M}{c^2}= 430$ m,

where is the gravitational constant, is the speed of light.

The fact that the dwarf stars of the spectral type M, considered to be the stellar analogue of the proton, have much larger radii, is explained by the fact that these stars are in the excited state. Oldershaw also uses the Schwarzschild formula for the radius of the black hole, in order to estimate the radius of the proton:

$R_p = \frac {2 \Gamma M_p}{c^2}= 0.8 \cdot 10^{-15}$ m,

where $\Gamma = 2.18 \cdot 10^{28}$ m³•s^–2•kg^–1 is the strong gravitational constant, assumed by Oldershaw, which is found by him through the ordinary gravitational constant and the similarity coefficients with the help of dimension relations.

Oldershaw assumes the medium-mass white dwarfs, based on their typical masses of about and , to be the stellar analogues of the positive helium ions He(3) and He(4) in the ground state. Multiplying the radius of the helium ion ( ) by $\Lambda$ he obtains the value of the order of m as the radius of typical white dwarfs. The radius of white dwarfs decreases with increasing of their mass, which is consistent with the decrease of the radii of hydrogen ions with increasing of their mass and charge. It can be noted that the morphology of planetary nebulae, surrounding some white dwarfs, is in many ways similar to the morphology of the electron-wave function in the atoms. The rotation periods of white dwarfs are grouped near the values of $250 \pm 100$ seconds and $850 \pm 100$ s. If we divide these periods by the coefficient of similarity in time $\Lambda$ , we obtain $4.8 \cdot 10^{-16}$ seconds and $1.6 \cdot 10^{-15}$ s, respectively. These periods are close to the oscillation periods of the electromagnetic emission in the electron transitions in helium ions. ^[4] This coincidence can be partly explained by the fact that the frequency of electron emission is close to the frequency of its orbital rotation in the atom and the electron motion is regulated by the action of strong gravitation, which is approximately equal in magnitude to the electric force. It turns out that the rotation of the electron in some ways is similar to the rotation of the surface of white dwarfs.

Oldershaw notes that many stellar systems demonstrate the dependence of the angular momentum on the square of the mass of the form , and the atomic systems – the dependence of the form , where the coefficients and have the dimension $\frac {[L]^2}{[M] [T]}$ . The ratio can be found using the similarity coefficients and the dimension theory:

$\frac {K}{k}= \frac {\Lambda^2}{X \Lambda}= \frac {\Lambda}{X}= 3\cdot 10^{-39}.$

The logarithm of the ratio is equal to -38.51, which is consistent with the average empirical estimates, giving the value $-38.41 \pm 3.5$ . Similarly, the correlation is derived for the dependences between the magnetic moment and the spin of stellar and atomic systems: $\mu_s=K_{\mu} J$ , $\mu_n=k_{\mu} j$ . From the similarity coefficients it follows that $\lg {\frac { K_{\mu}}{ k_{\mu}}} = -19.31$ , and the observations give $-20.36 \pm 2.43$ .

The model of S. Fedosin

The Solar system

The atomic masses are almost entirely determined by the masses of their nuclei, ranging from 1.00794 Da = 1.6737∙10⁻²⁷ kg for hydrogen up to about 207.9766521 Da for the heaviest stable isotope – lead Pb(208). More massive atoms contain radioactive nuclei and decay with time. The masses of main-sequence stars are usually not more than 50 solar masses , and can be less than .

To determine the analogue of the Solar system at the atomic level Sergey Fedosin applied the mathematical procedure based on two ideas: 1) The number of planets in the Solar System is 8, if we do not assume Pluto to be a real planet due to its small mass and size (almost like the asteroid Ceres), very large orbital inclination to the ecliptic, the significant eccentricity, slow proper rotation, the direction of its intrinsic angular momentum which is not perpendicular to the ecliptic plane (like in the case of most of other planets) but is in parallel to the ecliptic. 2) The masses of stars, including the Sun, are discrete almost the same way as it happens in the case of atoms.

Hence it follows that the Solar system by the number of planets, as the analogues of electrons, can be similar to the atom of the isotope of oxygen or fluorine, with the corresponding atomic number . To verify this assumption we make the proportion:

$M_s / M_c=A / A_c , \qquad\qquad (1)$

where is the exactly known mass of some star, is the mass number for this star.

Equation (1) is similar to the equation for the mass ratio of the two nuclides and the ratio of their mass numbers. From (1) we can determine the mass number of the star through its mass: $A= A_c \frac {M_s} {M_c}$ . If the discreteness of the stellar masses were exact enough, then in case of the correct choice of the mass number for the Sun, the mass numbers of various stars would be almost integer numbers, and the condition would be satisfied:

$F(A_c) = \sum^{n}_{i=1} { \mid A_i- [A_i] \mid } \rightarrow 0,$

where is the integer part of the number for the i-th star, and the function with some choice of has the minimum.

The exact masses of the stars were found from the Svechnikov’s catalog, ^[5] and from the data of other authors, and the function was calculated for various in the range from 15 to 21. As a result it turned out that the minimum of the function is reached at , so that the Solar system is the analogue of the stable isotope of oxygen O(18). This implies the following: 1) The nucleus of the hydrogen atom corresponds to the star with the minimum mass of about , which is 58 Jupiter masses. Such stars are now discovered and are called brown dwarfs. 2) The coefficient of similarity in mass between the atoms and the main-sequence stars is equal to the ratio of the Sun’s mass to the mass of the nuclide with the atomic number equal to 18. This gives the value of the similarity coefficient $\Phi =6.654 \cdot 10^{55}.$ 3) The electron corresponds to the planet with the mass equal to 10.1 Earth masses, which is less than the mass of Uranus. ^[6]

Ordinary stars

The characteristics

The results of studies of various parameters of stars, averaged over the set of well-studied main-sequence stars, are given in Table 2. ^[6] For the stars with masses and less the more accurate average radii are additionally given in brackets, measured by the long-baseline interferometer. ^[7]

Table 2. The characteristics of main-sequence stars
Mass,	Spectral class	Radius,	Luminosity,	Temperature, $T_{eff}$ , К	Density, kg/m³	Bolometric stellar magnitude
26	O8	8.7	180000	40400	56	−8.4
20.5	O9	7.4	93600	37200	71	−7.7
13.3	B0	6	22400	28800	87	−6.1
11.1	B1	5.4	12900	26400	99	−5.5
9.4	B2.5	4.9	7850	24600	113	−5
6.55	B2.9	4.05	1990	19200	139	−3.5
6.11	B3	3.85	1484	18300	150	−3.2
4.89	B4	3.35	593	15600	183	−2.2
4.39	B5	3.1	344	14150	208	−1.6
4	B7	2.9	238	13350	230	−1.2
3.2	B8− B9	2.5	103	11650	289	−0.3
2.8	A0	2.25	66	11000	346	0.2
2	A5	1.75	20	9230	526	1.5
1.8	F0	1.6	13.7	8800	620	1.9
1.5	F5	1.4	6.54	7820	770	2.7
1.33	G0	1.28	4.1	7280	840	3.2
1.07	G5	1.05	1.49	6240	1300	4.3
0.85	K0	0.88 (0.8)	0,545	5300	1760	5.4
0.65	K5	0.72 (0.61)	0.22	4650	2480	6.4
0.52	M0	0.6 (0.48)	0.0944	4140	3400	7.3
0.22	M5	0.3 (0.23)	0.0065	3000	11500	10.2
0.11	M7.25	0.17 (0.13)	0.001	2520	31600	12.2
0.056	M8.5	0.128 (0.07)	0.0001	1630	38000	14.7

In Table 2 the characteristics of stars are given in relation to the mass , the radius and the luminosity of the Sun; the effective temperatures $T_{eff}$ of the stellar surface are given in Kelvins, the average densities of the stellar matter and their bolometric stellar magnitudes are given, which take into account the total emission from the stars. With this data we can plot various smooth curves, for example, the dependence of the stellar radius on their mass.

The correspondence between the atoms and the stars

Based on the characteristics of the stars from Table 2 and the assumption that the Solar system is the analogue of the oxygen isotope O(18), we can first build the average dependence of the spectral class of stars on their mass, and then with the help of relation (1) we can find the mass numbers of the stars as the function of the mass . Since the mass numbers of stars and of the atomic nuclei similar to them coincide, then it becomes possible to find the correspondence between the spectral classes of stars and the chemical elements according to Table 3. ^[6]

Table 3. Correspondence between the spectral classes of stars and chemical elements
Spectral class	Chemical elements
B0	Fr, Ra, Ac, Actinides, Ku, Nc, etc.
B1	Au, Hg, Tl, Pb, Bi, Po, At, Rn.
B2.5	Cs, Ba, La, Lanthanides, Hf, Ta, W, Re, Os, Ir, Pt.
B2.9	Ag, Cd, In, Sn, Sb, Te, I, Xe.
B3	Ru, Rh, Pd.
B4	Rb, Sr, Y, Zr, Nb, Mo, Tc.
B5	As, Se, Br, Cr.
B7	Cu, Zn, Ga, Ge.
B8−B9	Fe, Co, Ni.
A0	Sc, Ti, V, Cr, Mn.
A1	Ca
A2−A4	Ar, K.
A5−A6	Cl
A7−F0	S
F2	P
F3−F8	Si
F8.5	Al
F9−G0	Mg
G1	Na
G2−G4	Ne
G5	F
G7−K1	O
K2	N
K2.5−K7	C
M0	Be, B.
M4	Li
M5	He
M7.25	D (deuterium)
M8.5	H

Table 3 shows that almost all main-sequence stars correspond to the chemical elements of the periodic table. The stars of the spectral type O, which are supergiants, and the superheavy chemical elements are absent in the Table 3 due to their extremely small number. In particular, the estimate of the number of the stars of the spectral type O in the galaxy Large Magellanic Cloud gives the number not more than 1000, with the total number of stars in the galaxy of the order of 10¹⁰. ^[8]

Abundance of stars of different spectral types

Figure 1. The actual relative distribution of star concentration after recalculation in terms of their visibility. The numbers at the breaks of the curve show the mass numbers of the stars.

Discreteness of parameters of main-sequence stars reveals in the fact that the stars with some values of masses are much more prevalent in number than the stars with other values of masses. This is demonstrated by catalogs of stars, containing tens or even hundreds of thousands of stars which can be placed on the plane in the coordinates "the absolute stellar magnitude – the spectral class", with indication of their number in each point of the plane. For example, in the Michigan spectral catalogue of stars ^[9] we can clearly see that in the spectral classes near A0 and F5 there are local maxima of stars. With the help of Table 2 we can turn from the spectral classes of stars to the masses of stars, and from relation (1) we can calculate the atomic masses of these stars. The same result is obtained from Table 3, connecting the spectral classes of stars and the corresponding chemical elements. This allows us to build on the basis of the Michigan spectral catalogue the dependence of the relative abundance of stars on their mass number.

In this case it is necessary to make a correction that the observed abundance of stars differs from the actual due to different luminosity of stars (bright stars are visible from far away at the distances, at which the existing faint stars stop being detected). If $N_{s}$ is the visible number of stars with the luminosity , then the real number of these stars in the first approximation is given by: ^[6]

$\lg G=2,1+\lg N_{s}-1,5\lg {{\frac {W_{s}}{W_{c}}}}.$

Figure 2. The chemical composition of the Sun according to the Allen summary. ^[10] The number of silicon atoms is assumed to be 10⁶.

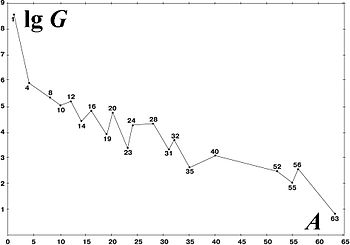
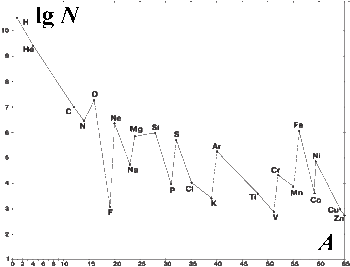
The actual distribution of stars is shown in Figure 1, and it can be compared with the distribution of chemical elements. There are two main distributions of chemical elements: the first – for meteorites and the Earth's crust, and the second – for the Sun, planetary nebulae and stars. It turns out that there is close similarity between the distribution of the abundance of stars in the Galaxy, and the distribution of chemical elements in the Sun and stars in Figure 2. The similarity of both distributions is also stressed by the fact that in the range of mass numbers from 35 to 55 in both figures there is a dip, after which in Figure 2 the so-called iron peak begins. The figures show that in the Universe the low-mass chemical elements dominate and the stars corresponding to them.

Binary and multiple stars

Over 70 % of the observed stars are part of binary and multiple systems, ^[11] just as atoms are combined in molecules. With the help of determining the elements of orbits of the visual binary stars we can very accurately find the masses of the components. The study of the catalogues of binary stars allows us to show that most of the stars in the pairs are connected the same way as the atoms, corresponding to them by mass, form the chemical molecules. With the distances between the components of pairs less than 50 a.u. there are extremums in the distribution of the angular separation of the components, similar to the distribution of the bond lengths in diatomic molecules. The ratio of the distances between the components of stars to the bond length of the corresponding molecule gives the estimate of the coefficient of similarity in size, which is close to the coefficient of the similarity in size between the hydrogen atom and the corresponding planetary system: $P_0 = 5.437 \cdot 10^{22}$ . ^[6]

The distribution of the orbital planes of binary stars in the Galaxy Milky Way is rather chaotic, but the long-period stellar pairs mostly have the same direction of rotation as the Galaxy as a whole. ^[12] For the short-period binaries the situation is the opposite, which is the consequence of the differential rotation and the dynamics of interaction in approaching of the stars. In the Galaxy the stars are grouped together in tight groups, open and globular clusters, are part of the disc and the spherical component. If we count the stars to be similar to atoms, then from the point of view of the similarity of matter levels all the known galaxies, by the number of their component stars, are similar to the dust particles of the corresponding chemical composition, and the masses and sizes of galaxies and dust particles are connected by the similarity coefficients. The concentration of stars in the Galaxy is of such kind that it corresponds to sufficiently rarified gas of complex chemical composition, and only with the radius of less than 0.047 pc the "solid substance" will appear, which is similar by its density to coke, and is rotating as a solid body relative to the center of mass of the Galaxy. In the central part of the Galaxy and in the disc the massive stars dominate, corresponding to the atoms of metals and heavy non-metals, and the lighter stars in the spherical component of the Galaxy are the analogues of volatile gases such as oxygen, nitrogen, hydrogen, etc. In addition, if we move from the Galactic center and consider the amount of metals in the stars come across, then it will continuously decrease, reflecting the logical evolution of stars in galaxies.

Discreteness of parameters of cosmic objects does not stop at the stars, it is found at the level of galaxies. For example, our Galaxy has the mass number and approximately corresponds to oxygen. This follows from the coefficients of similarity and the number of dwarf galaxies surrounding the Galaxy like the electrons in the oxygen atom. The tight group of galaxies, consisting of the Galaxy and the Large and Small Magellanic Clouds, can be considered as the water molecule. ^[6] The large neighboring galaxy, the Andromeda Galaxy, has the mass number up to , and forms a kind of molecule with the Triangulum Galaxy ().

Characteristic speeds

The characteristic speed of the matter particles of the object, held in the gravitational field, is given by: ^[6]

$E_0=mC^2_{x}= \frac{ k G m^2}{ 2 R}, \qquad\qquad (2)$

where and are the mass and the radius of the object, is the gravitational constant, is the coefficient depending on the matter distribution, in the case of the uniform mass density .

This equation is the relation between the internal energy of the object, as the kinetic energy of its matter particles, and the energy of the object in the gravitational field. The absolute value of full energy is proportional to the mass, which is revealed as the mass–energy equivalence. From equality (2) we can find the characteristic speeds through the masses of objects, in this case the discreteness of masses of main-sequence stars implies the discreteness of their characteristic speeds and of the total energies of stars. For the stars with the minimum mass the characteristic speed of its matter is $C_{s}=220$ km/s. The analogue of this star is the proton, the characteristic speed of the matter of which is equal to the speed of light . The ratio of these speeds specifies the coefficient of similarity in speed $S_0= \frac {C_{s}} {c}=7.34 \cdot 10^{-4}$ for the hydrogen system.

If we consider the hydrogen-like atoms and the stellar-planetary systems corresponding to them, then the velocity of motion of the electron in the atom is proportional to the charge of the atomic nucleus, and the velocity of the planet is proportional to the mass number . It follows that the coefficient of similarity in speed between atoms and stars is proportional to the ratio : $S =S_0 \frac {A} {z}$ . Assuming that the same holds for the speed of the matter in the star, for the characteristic speed and the total energy of main-sequence stars we obtain the expressions:

$C_{x}=C_s \frac{A}{z},$

$E_s= - M_s C^2_{s} (\frac{A}{z})^2.$

These ratios well approximate the results of numerous calculations of the total energies of stars, made in different ways by various authors (see references in Fedosin SG, 1999. ^[6]). For hydrogen-like systems the coefficient of similarity in size has the form: $P=P_0 \frac{z}{A}$ .

The speeds $C_{x}$ are boundary for the maximum speeds of stellar surfaces’ rotation, as well as for the average velocities of the motion of stars relative to the stellar systems in which these stars have been formed (the principle of local stellar velocity).

The angular momenta

The observed discreteness of masses, typical sizes and angular velocities of rotation of stars leads to the discreteness of the angular momentum of the proper rotation of stars. To estimate the value of the characteristic angular momentum for main-sequence stars, we should multiply the Dirac constant by the coefficients of similarity:

$\hbar_s= \hbar \Phi P S = \hbar \Phi P_0 S_0 = 2.8 \cdot 10^{41}$ J∙s.

The quantity $\hbar_s$ specifies the orbital angular momentum of the planet, the analogue of the electron, during its rotation in the hydrogen system around the star of minimum mass, which is the analog of the proton. On the other hand, $\hbar_s /2$ is almost exactly equal to the angular momentum of the proper rotation of the Sun, which is equal to $1.6 \cdot 10^{41}$ J∙s. ^[13] The characteristic angular momentum $\hbar_s$ can be also compared with the maximum angular momentum of rotation of the star of minimum mass. In case of the limiting rotation of the star at its equator, the acceleration of gravitation and the centripetal acceleration are equal:

$\frac {G M_s}{R^2_s}= \frac {u^2}{R_s},$

where is the equatorial velocity.

In view of this and the parameters of the star of minimum mass from Table 2 the limiting spin of the star, the analogue of the proton, is equal to:

$L_s = K_s M_s R_s u = K_s M_s \sqrt { G M_s R_s} = K_s \cdot 4 \cdot 10^{42}$ J∙s,

where is the coefficient depending on the distribution of matter in the star.

The similar formula for the limiting spin of the proton gives:

$L_p = K_p M_p \sqrt { \Gamma M_p R_p} = K_p \cdot 7.8 \cdot 10^{-34}$ J∙s,

where is the coefficient depending on the distribution of matter in the proton, $\Gamma$ is the strong gravitational constant.

The Heisenberg uncertainty principle for changing the energy of the quantum process and the time interval of this process sets the limiting connection with the Dirac constant:

$\Delta E \Delta t \geq \frac{\hbar}{2}.$

The similar in the meaning relation for the stellar level is obtained if in the free fall of the matter with the mass to the volume with the radius during the time , the total gravitational binding energy is released and the star of minimum mass is formed:

$E_s \cdot t_s = \frac{ k G M^2_s}{ 2 R_s} \cdot \sqrt {\frac {2R^3_s}{G M_s}} = k \cdot 2 \cdot 10^{42}$ J∙s,

where the gravitational acceleration is estimated by the formula $g \approx \frac {G M_s}{R^2_s}$ , and the radius of the fall – by the formula $R_s \approx \frac {g t^2_s}{2}$ .

In this ratio the product of the energy change and the time of the change coincides by the order of magnitude with $\hbar_s$ . In the Galaxy during its formation the separation of gas clouds into fragments takes place, of which the stars are formed. The mass of the matter, of which this or that star is formed, is not isolated, since it is influenced by the forces of gravitation from the other fragments. As a result, the real time of the formation of stars with the masses less is determined by the time of the accretion of the shell $t_{ac}$ , and with large masses – by the Kelvin-Helmholtz time $t_{KH}$ . The product of stellar energy and the real time of their formation in the Galaxy sets the new characteristic angular momentum $\hbar_o$ . This angular momentum is close by its value to the average orbital angular momentum of the stars in the Galaxy. For the Sun the orbital angular momentum is equal to $(1.15-1.53) \cdot 10^{56}$ J∙s, and using the coefficients of similarity for the galaxies we obtain $\hbar_o = 3,4\cdot 10^{56}$ J∙s. ^[6]

The magnetism of stars

Figure 3. The field strength for magnetic stars of different spectral types. ^[14]

All the known stars can be divided into two great classes – non-magnetic and magnetic. This division is to some extent conventional, since non-magnetic stars have small total dipole magnetic field, but in some points of the surface they can have significant local magnetic fields. Magnetic stars have the dependence between the angular momentum of the proper rotation and the total magnetic moment, and we can observe the change of sign and overturn of the dipole magnetic moment like on the Sun. Magnetic stars usually rotate 2 – 4 times more slowly than non-magnetic, and their matter composition has excess of elements of the type of iron and rare-earth elements.

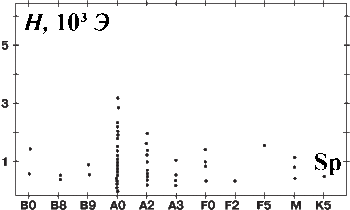
Figure 3 shows the distribution of magnetic stars by spectral classes and the field strengths at the surface, showing clear discreteness of the magnetic properties. The stars of the spectral class A0 have the largest magnetic fields. If using Table 3 we find the analogues of these stars at the level of atoms, we shall obtain the atomic nuclei of the type Sc (45), Ti (47), Ti (49), V (50), V (51), Cr (53), Mn (55), Co (59). Indeed, among the atomic nuclei these nuclei have the largest magnetic moments, except the extremely rare nuclides Nb (93), Tc (99), In (113). The magnetic stars are seen in the spectral classes near A2, A3, F0, F2, F5, which correspond to the magnetic nuclides Ca (43), K (39-41), Cl (35-37), S (33-35), P ( 31), Si (29), Al (27). Finally, to the spectral class M such magnetic nuclides correspond as He (3), Li (7), Be (9), B (10-11). How can we explain such similar distributions by the magnetic properties of the stars and the atomic nuclei similar to them? According to one of the assumptions, the similarity of stars and the atomic nuclei by their masses is supplemented by the fact that the stars contain increased concentrations of the atoms to which these stars are similar.

There are two main hypotheses describing the magnetic fields of stars. The dynamo theory suggests that the self-sustaining magnetic field is possible due to the convective fluxes of the conductive matter in the interior of stars and planets, the effect of electromagnetic induction and the centripetal forces of rotation. However, there is still no consistent mechanism of dynamo even for the Sun, which would accurately take into account the change of sign of its dipole magnetic field. ^[15] In another hypothesis the origin of the magnetic field of stars is associated with their rotation. It is noted that the magnetic moments of planets, stars and even galaxies in the dependence "magnetic moment – spin" are located within two parallel lines. ^[6] The upper line corresponds in view of the similarity coefficients to the Bohr magneton, and the lower line corresponds to the nuclear magneton. The inclination of the lines is equal to unity, so that the magnetic moments are directly proportional to the spin (for the planets they are proportional to the spin of the planets’ nuclei). In his electrokinetic model Sergey Fedosin justifies the emergence of the magnetic field based on the concept of separation of charges in the matter of cosmic bodies. In this model, the magnitude of the magnetic field is proportional to the angular velocity of the body’s rotation and the radius of the convective layer. At the same time the periods of change of the polarity of the magnetic field of the Earth and the Sun are calculated through the sizes of the convective layer and the convection speed of the matter. The solar activity is the consequence of the periodic conversion of the thermal energy into the electromagnetic form of energy. ^{[16] [17]}

Compact stars

In contrast to main-sequence stars, the mass density of white dwarfs and neutron stars is much higher, equal by the order of magnitude to 10⁹ kg/m³ and 10¹⁷ kg/m³, respectively. If in ordinary stars the gravitational pressure is balanced by the pressure of thermally ionized plasma, in white dwarfs – by the pressure of electrons, then in neutron stars the force of gravitation is counteracted by the pressure of the degenerate neutron gas. White dwarfs are essentially the cores of ordinary stars, in which thermonuclear reactions reach the final stage with ejection of the stellar shell at the stage of red giant. It is considered that all stars with masses up to must turn into white dwarfs. There is the Chandrasekhar limit, equal to approximately , above which the white dwarf can become a neutron star. The chemical composition of white dwarfs is determined by the initial mass of stars, of which they are formed. Depending on the initial mass, thermonuclear reactions occur with hydrogen burning and its transformation into helium, helium also can burn, giving carbon and more massive nuclei of oxygen, neon, magnesium. As a result dense hydrogen stars of low mass can appear, as well as helium, carbon and more complex composition white dwarfs, and the discreteness of the mass of main-sequence stars is supplemented by additional discreteness associated with the evolution and the chemical composition of the emerging white dwarfs.

The theoretical range of changing of the masses of neutron stars is from to . The lower mass limit is associated with the instability of the matter in the form of neutron liquid due to the small gravitational pressure in the star, which can lead to the destruction of low-mass star in explosive way. The upper mass limit is called the Tolman–Oppenheimer–Volkoff limit. It is assumed that with large masses the gravitational pressure overcomes the internucleon repulsive forces in the star and it collapses into a denser object of the type of hypothetical quark stars or black holes. Most of the observed masses of neutron stars, found accurately enough in binary systems with pulsars, differ little from the Chandrasekhar limit and are equal to . Probably, some neutron stars reach the mass and more. Such discreteness of masses is explained by the equation of the state of matter and the standard way of formation of stars in supernova outbursts, when the excess mass is expelled from the surface of the emerging neutron star. The radii of the stars are in the range from 11 to 15 km, the uncertainties here arise from inexact knowledge of the equations of state in the theoretical modeling, and from the ambiguity of interpretation of the observed radius of the photosphere relative to the radius of the star.

Using relation (2) we can calculate that the characteristic speed of the matter particles $C_{x}$ for white dwarfs is in the range from 930 to 4000 km/s, and for neutron stars – from 17000 to 71000 km/s. For planets the speed $C_{x}$ does not exceed 52 km/s (for the Earth it is 4.3 km/s).

If in the Oldershaw hierarchical model the similarity coefficients between the atoms and the stars do not depend on the type of stars, then in the Fedosin model it is not so. As the model of the proton the neutron star is considered with the mass $M_s = 2.7 \cdot 10^{30}$ kg and the radius $R_s = 1.2 \cdot 10^{4}$ m and the characteristic speed $C_s = 6.8 \cdot 10^{7}$ m/s. The corresponding parameters of the proton: the mass $M_p = 1.67 \cdot 10^{-27}$ kg, the radius $R_p = 8.7 \cdot 10^{-16}$ m, the characteristic speed $c = 2.99 \cdot 10^{8}$ m/s (the speed of light). Hence, we find the coefficients of similarity: in mass $\Phi' =M_s /M_p=1.62 \cdot 10^{57}$ , in sizes $P' =R_s /R_p =1.4 \cdot 10^{19}$ , in speeds . The coefficient of similarity in the time of processes’ duration has the form $\Pi' =P'/S'=6.1 \cdot 10^{19}$ , and it is not equal to the coefficient of similarity in size. ^[6] ^[17]

With the help of the coefficients of similarity and the relations of dimension of physical quantities we can calculate the characteristic angular momentum of compact objects in the form of the stellar Dirac constant, the electric charge and the magnetic moment of the star, the analogue of the proton:

${\hbar'}_s = \hbar \Phi' P' S' = 5.5 \cdot 10^{41}$ J∙s,

$Q_s = e (\Phi' P')^{0.5} S' = 5.5 \cdot 10^{18}$ C,

$P_{ms} = P_{mp} {\Phi'}^{0.5} {P'}^{1.5} {S'}^2 = 1.6 \cdot 10^{30}$ J/T.

Here and $P_{mp}$ are the elementary charge and the magnetic moment of the proton.

According to the substantial neutron model and the substantial proton model it is assumed that the neutron’s analogue is the ordinary neutron star, and the proton’s analogue is the magnetar carrying the electric charge and the magnetic moment $P_{ms}$ . Due to its large charge the magnetar is able to generate high-energy cosmic rays. ^[17] For comparison, in the Oldershaw model, based on his similarity coefficients for the stars, the significant electrical charge of the order of $1.5 \cdot 10^{18}$ C is admitted.

The pion is the hadron of the smallest mass, among the compact objects its analogue is the neutron star with the mass . The white dwarf with the mass and the radius $1.5 \cdot 10^7$ m corresponds to muon. Since the charged pion turns into the muon, then it is expected that the neutron star, the analogue of the pion, also turns into the white dwarf with time, due to the reactions of weak interaction in the matter of the star. The atomic nuclei as the compound of nucleons correspond at the level of stars the groups of neutron stars that are closely bound by gravitational forces and gravitational torsion fields. Such groups of stars can be located in massive X-ray systems and in the centers of galaxies. Neutron star, proton, as well as Metagalaxy, considered as relativistic uniform system, turn out to be extreme objects in terms of the dependence of their gravitational field on the radius. ^[19]

References

Oldershaw, R. L. Quantitative Scaling For The Self-Similar Hierarchical Cosmology. – International Journal of General Systems, 1986, Vol. 12, P. 137-148.
Mandelbrot, B. B. (1982). The Fractal Geometry of Nature, W. H. Freeman, San Francisco.
Oldershaw, R. L. Speculations in Science and Technology, 1991, Vol. 14, P. 193.
Oldershaw, R. L. Speculations in Science and Technology, 1989, Vol. 12, P. 135.
Свечников М.А. Каталог орбитальных элементов, масс и светимостей тесных двойных звёзд. – Иркутск, изд-во Иркутского университета, 1986.
^6.00 ^6.01 ^6.02 ^6.03 ^6.04 ^6.05 ^6.06 ^6.07 ^6.08 ^6.09 ^6.10 Fedosin S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik, Perm: Style-MG, 1999, ISBN 5-8131-0012-1. 544 pages, Tabl.66, Ill.93, Bibl. 377 refs.
B.-O. Demory et al. Mass-radius relation of low and very low-mass stars revisited with the VLTI. arXiv:0906.0602v1, 2 Jun 2009.
Humphreys R.M., Davidson K. Studies of luminous stars in nearby galaxies. Comments of the evolution of the most massive stars in the Milky Way and the large Magellanic Cloud. – ApJ, 1979, Vol. 232, P. 409-420.
Houk N., Fesen R. HR diagrams derived from the Michigan spectral catalogue. – in “The HR Diagram”, eds. A.G. Davis Shilip and D.S. Hayes, P. 91-98, IAU, 1978.
Мартынов Д.Я. Курс общей астрофизики. М.: Наука, 1988.
Бэттен Н. Двойные и кратные звёзды. М.: Мир, 1976.
Бражникова Э.Ф. О галактической ориентации орбит спектрально-двойных звёзд. Астрономический журнал, 1971, Т. 61, Вып. 3.
Аллен К.У. Астрофизические величины. М.: Мир, 1977.
Тутуков А.В., Рубен Г.В. Эволюция звёзд с магнитным полем. Научные информации Астрономического Совета АН СССР, 1974, Вып. 31, Стр. 5-16.
Tobias S.M. "The Solar Dynamo". Phil. Trans. A, 2002, Vol. 360, P. 2741–2756. doi:10.1098/rsta.2002.1090.
Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009-2011, 858 pages, Tabl. 21, Pic. 41, Ref. 293. ISBN 978-5-9901951-1-0. (in Russian).
Fedosin S.G. Generation of magnetic fields in cosmic objects: electrokinetic model. Advances in Physics Theories and Applications, Vol. 44, P. 123—138 (2015).
^18.1 ^18.2 Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9.
Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.

External links

Discreteness of stellar parameters in Russian

На русском языке