Спин

Из проекта Викизнание

Спин в квантовой механике обозначает собственный момент импульса отдельных элементарных частиц и их связанных состояний в виде ядер и атомов. В отличие от орбитального момента импульса, спин не связан с перемещением в пространстве центра инерции частицы, и является её внутренней характеристикой. Поскольку спин является вектором, он имеет направление в пространстве и отражает вращение составных элементов частицы. У ядер и атомов спин определяется по правилам квантовой механики как векторная сумма орбитальных и спиновых моментов импульса составляющих частиц, с учётом квантования проекций моментов импульса. При увеличении размеров системы и количества частиц в ней орбитальные моменты импульса могут быть много больше, чем спиновые моменты импульса. Это приводит к тому, что спин макросистемы в виде отдельного тела почти полностью зависит от орбитального вращения элементов вещества тела вокруг некоторой оси.

В квантовой механике квантовые числа для спина не совпадают с квантовыми числами для орбитального момента частиц, что приводит к неклассической трактовке спина. Кроме этого, у спина и орбитального момента частиц возникает различная связь с соответствующими магнитными дипольными моментами, сопровождающими любое вращение заряженных частиц. В частности, в формуле для спина и его магнитного момента гиромагнитное отношение не равно 1.

Концепция спина у электрона привлекается для объяснения многих явлений, таких как расположение атомов в периодической системе химических элементов, тонкая структура атомных спектров, эффект Зеемана, ферромагнетизм, а также для обоснования принципа Паули. Недавно возникшая область исследований, называемая «спинтроника», занимается манипуляциями спинов зарядов в полупроводниковых устройствах. В ядерном магнитном резонансе используется взаимодействие радиоволн со спинами ядер, позволяющее осуществлять спектроскопию химических элементов и получать изображения внутренних органов в медицинской практике. Для фотонов как частиц света спин связывается с поляризацией света. Математическая теория спина была использована для построения теории изоспина элементарных частиц.

6.1 Оператор спина
6.2 Спин и принцип запрета Паули
6.3 Спин и вращения системы координат
6.4 Спин и лоренцевские преобразования
6.5 Матрицы Паули и операторы спина
6.6 Измерение спина вдоль осей x, y, z
6.7 Измерения спина вдоль произвольной оси
6.8 Совместимость измерений спина

7 Использование концепции спина в науке и технике
8 Обобщение спина
9 Сущность спина

9.1 Спин электрона
9.2 Характерный спин
9.3 Предельные соотношения для нуклонов

10 Ссылки
11 Справочная литература
12 Внешние ссылки
13 Смотри также

История

В 1922 г. был описан опыт Штерна — Герлаха, который обнаружил пространственное квантование направления магнитных моментов у атомов. Впоследствии, в 1927 г. это было интерпретировано как доказательство существования спина у электронов. ^[1]

В 1924 г. Вольфганг Паули ввёл двухкомпонентную внутреннюю степень свободы для описания эмиссионных спектров валентного электрона в щелочных металлах. Это позволило ему сформулировать принцип Паули, согласно которому в некоторой системе взаимодействующих частиц у каждого электрона должен быть свой собственный неповторяющийся набор квантовых чисел (все электроны в каждый момент времени находятся в разных состояниях). Поскольку физическая интерпретация спина у электрона была неясна с самого начала (и это имеет место до сих пор), в 1925 г. Ральф Крониг (ассистент известного физика Альфреда Ланде) высказал предположение о спине как результате собственного вращения электрона. Однако согласно Паули, в таком случае поверхность электрона должна вращаться быстрее скорости света, что кажется невероятным. Тем не менее осенью 1925 г. Дж. Уленбек и С. Гаудсмит постулировали, что электрон обладает спином $~s={\frac{1}{2}}{\hbar}$ в единицах постоянной Дирака $~\hbar$ , и спиновым магнитным моментом, равным магнетону Бора. Это предположение и было принято научным сообществом, поскольку удовлетворительно объясняло известные факты.

В 1927 г. Паули модифицировал открытое ранее Шрёдингером и Гейзенбергом уравнение Шрёдингера с целью учёта спиновой переменной, используя спиновые операторы и матрицы Паули. Модифицированное таким образом уравнение носит сейчас название уравнение Паули. При таком подходе у электрона появляется новая спиновая часть волновой функции, которая описывается спинором — «вектором» в некотором абстрактном спиновом пространстве.

В 1928 году Поль Дирак построил релятивистскую теорию спина на основе четырёхкомпонентной величины, называемой биспинором.

Спиновое квантовое число

Спин элементарных частиц

В теории элементарных частиц обычно предполагается, что фотон, электрон и кварки не делятся на более мелкие части и являются самыми «элементарными». Однако спин, который приписывается этим частицам, слишком велик, чтобы его можно было объяснить вращением составляющего вещества при известных оценках размеров частиц. Поэтому для этих частиц спин полагается некоторым внутренним свойством, наподобие массы и заряда, требующим особого, пока ещё не известного обоснования.

В квантовой механике спиновый момент импульса любой системы квантуется. Амплитуда или длина вектора спинового момента в каждом состоянии равна:

$S = \hbar \, \sqrt{s (s+1)},$

где $\hbar$ есть постоянная Дирака, а спиновое квантовое число s является положительным целым или полуцелым числом (0, 1/2, 1, 3/2, 2, ...) и зависит от типа частицы. В противоположность этому орбитальный момент импульса имеет только целые квантовые числа.

Спин составных частиц

К составным частицам можно отнести атомные ядра, состоящие из нуклонов, а также адроны, согласно кварковой концепции состоящие из кварков. Спин составной частицы находится векторным суммированием орбитальных и спиновых моментов импульса всех составляющих её частиц, с учётом правил квантового сложения, и также квантуется, как любой момент импульса. В квантовой механике каждая составная частица имеет некоторый минимально возможный спин, не обязательно равный нулю (в этом состоянии моменты импульса составляющих частиц частично компенсируют друг друга, уменьшая спин составной частицы до минимума). Если же моменты импульса составляющих частиц складываются, то это может приводить к состояниям, в которых составная частица имеет значительный спин. Так, одним из наибольших спинов среди адронов обладает барионный резонанс Δ(2950) со спином 15/2 $\hbar$ . Спин ядер из-за их относительно больших размеров может превышать 20 $\hbar$ .

В качестве других примеров можно привести Δ-барион и какой-либо нуклон, протон или нейтрон. В кварковой теории у Δ-бариона спины всех трёх кварков складываются, давая спин 3/2. В нуклоне спины двух кварков противоположны и вычитаются, и спин 1/2 нуклона равен спину третьего кварка. Картина однако усложняется тем, что в нуклонах кроме кварков предполагаются глюоны как переносчики взаимодействия, а также виртуальные частицы. Вследствие этого распределение момента импульса между кварками и глюонами в адронах точно не определено.

Спин атомов и молекул

Размеры атомов и молекул много больше размеров атомных ядер, так что спин какого-либо атома определяется его электронной оболочкой. В заполненных атомных оболочках количество электронов чётно и их суммарный момент импульса равен нулю. Поэтому за спин атомов и молекул ответственны неспаренные электроны, находящиеся обычно на внешней оболочке. Считается, что именно спин неспаренных электронов приводит к явлению парамагнетизма.

Ниже указаны спины некоторых элементарных и составных частиц.

спин	общее название частиц	примеры
0	скалярные частицы	π-мезоны, K-мезоны, хиггсовский бозон, атомы и ядра ⁴He, чётно-чётные ядра, парапозитроний
1/2	спинорные частицы	электрон, кварки, протон, нейтрон, атомы и ядра ³He
1	векторные частицы	фотон, глюон, векторные мезоны, ортопозитроний
3/2	спин-векторные частицы	Δ-изобары, гравитино
2	тензорные частицы	гравитон, тензорные мезоны

Связь между спином и статистикой

В квантовой механике волновая функция системы из нескольких одинаковых частиц может быть либо симметричной (неизменной) относительно перестановки местами двух любых частиц, либо антисимметричной, что приводит к умножению волновой функции на −1. В первом случае говорят, что частицы подчиняются статистике Бозе – Эйнштейна, а сами частицы называются бозонами. Во втором случае частицы называются фермионами и подчиняются статистике Ферми – Дирака.

В 1940 г. Паули доказал теорему о связи спина со статистикой, которая утверждает: «Частицы с целым спином (s = 0, 1, 2, …) являются бозонами, а частицы с полуцелым спином (s = 1/2, 3/2, …) – фермионами». ^[2] Это означает, что симметрия волновой функции относительно перестановки одинаковых частиц определяется спиновыми квантовыми числами данных частиц. Свойством частиц – бозонов является то, что в одном и том же квантовом состоянии может находиться одновременно множество частиц. У фермионов каждая частица в соответствии с принципом запрета Паули имеет квантовое состояние, не совпадающее с состояниями других частиц.

Спиновый магнитный момент

Спин является частью полного механического момента импульса частицы, и если последняя заряжена, то спину по формулам классической электродинамики можно поставить в соответствие определённый магнитный дипольный момент. При этом часто используется так называемое гиромагнитное отношение как отношение магнитного момента к механическому моменту. Для частицы с массой m, зарядом q и спином S спиновый магнитный момент μ равен:

$~\mu = g \, \frac{q}{2m}\, S,$

где безразмерная величина g называется g-фактором. Для чисто орбитального (например, кругового) вращения элементов заряженного вещества частицы вокруг оси g-фактор должен быть равен 1. У электрона g-фактор почти точно равен 2, что существенно отличает спин от орбитального вращения. Отличие g-фактора электрона от 2 в квантовой электродинамике обосновывается как следствие взаимодействия заряда электрона с окружающим электромагнитным полем, включая самодействие поля электрона. За счёт спинового магнитного момента частицы могут взаимодействовать друг с другом и с внешними магнитными полями.

Как правило принимается, что нейтрино электрически нейтральны, но при наличии некоторой ненулевой массы покоя у них не исключается наличие магнитного момента.^[3] ^[4] ^[5] Формула для предполагаемого магнитного момента нейтрино $~\mu_{\nu}$ имеет вид:

$~\mu_{\nu}\approx 3\times 10^{-19} \mu_{B} m_{\nu} ,$

где $~m_{\nu}$ есть масса-энергия нейтрино в электронвольтах, $~\mu_{B}$ – магнетон Бора. Если исходить из оценок массы-энергии нейтрино, не превышающих значение 1 eV, то из соображений ограниченности электромагнитной энергии по сравнению с энергией покоя ожидается, что магнитный момент нейтрино не превышает 10⁻¹⁴ $~\mu_{B}$ . ^[6] Из имеющихся экспериментальных данных магнитный момент нейтрино не превышает 1,2 × 10^–10 от величины магнитного момента электрона.

Наличие спина у составных частиц приводит к соответствующему спиновому магнитному моменту. Многие нейтральные адроны, невзирая на равенство нулю у них суммарного заряда, обладают магнитным моментом, причём направление магнитного момента обычно противоположно спину. Это ясно указывает на их сложную внутреннюю электромагнитную структуру. С точки зрения кварков, которым приписываются различные заряды, магнитные моменты адронов приблизительно могут быть получены как комбинации спиновых и орбитальных магнитных моментов составляющих адроны кварков.

В веществе большинства тел магнитные моменты атомов направлены случайным образом в различные стороны и взаимно вычитают друг друга, обращая суммарное магнитное поле в нуль. В ферромагнитных материалах ниже температуры Кюри возникает внутренняя магнитная упорядоченность за счёт доменной структуры. В каждом домене магнитные моменты атомов выстраиваются приблизительно параллельно, усиливая общее магнитное поле. В свою очередь магнитные поля доменов суммируются векторно, приводя к достаточно устойчивой намагниченности ферромагнетиков и превращая их в магниты.

Магнитная упорядоченность возникает и под действием внешнего магнитного поля. В парамагнитных материалах магнитные моменты атомов устанавливаются вдоль приложенного магнитного поля, тогда как в диамагнитных веществах атомные магнитные моменты направлены против поля и ослабляют его. Электронный парамагнетизм есть следствие ориентации электронных магнитных моментов, которые начинают прецессировать вдоль направления поля. Диамагнетизм вытекает из действия закона электромагнитной индукции, согласно которому при изменении магнитного потока в системе зарядов возникает электродвижущая сила. Появляющееся по действием этой силы движение зарядов приводит к магнитному полю, направленному противоположно исходному магнитному полю (правило Ленца). Считается, что существенная доля магнитных моментов атомов связана со спином электронов, хотя вклады в магнитные эффекты делают и орбитальные магнитные моменты электронов.

Ориентация спина

Квантовое число проекции спина и мультиплетность

Поскольку спин является вектором момента импульса, он имеет и амплитуду и направление в пространстве. В квантовой механике используется понятие о проекции момента импульса на некоторую выделенную ось (обычно направление этой оси в пространстве задаётся внешним магнитным полем). Пусть выделенное направление фиксируется осью z используемой системы отсчёта. Тогда возможные проекции спина на эту ось имеют значения:

$\hbar \cdot s_z, \qquad s_z = - s, - s + 1, \cdots, s - 1, s$

где s есть спиновое квантовое число для частицы или системы частиц. Общее число проекций спина s_z равно 2s+1. В стандартной теории в приближении спин-орбитальной связи число 2s+1 называется мультиплетностью спиновой системы. В частности, для частиц со спином 1/2 получается только два значения для проекции спина: s_z = +1/2 и s_z = -1/2. Отсюда следует, что для электрона в водородоподобном атоме мультиплетность равна 2, а спектры таких атомов имеют дублетную природу. При наличии двух электронов, как это происходит в гелии, суммарный спин обоих электронов равен 0 либо 1. Соответственно, мультиплетность будет равна 1 для парагелия с одиночными линиями в спектре, и равна 3 для ортогелия с триплетными линиями в спектре.

Вектор спина

В каждом квантовом состоянии можно ввести вектор спина $\lang S \rang$ , чьими компонентами являются ожидаемые значения проекций спина на оси системы координат $\lang S \rang = [\lang s_x \rang, \lang s_y \rang, \lang s_z \rang]$ . Этот вектор указывает "направление" спина, соответствующее в классическом пределе оси вращения. В квантовомеханических вычислениях вектор спина имеет особенность – его компоненты s_x, s_y и s_z не могут быть измерены одновременно из-за квантового принципа неопределённости Гейзенберга. Однако для статистически больших наборов частиц при одинаковых начальных квантовых состояниях, как это имеет место в опыте Штерна — Герлаха, вектор спина и связанный с ним вектор магнитного момента имеют хорошо определённое экспериментально направление – оно задаётся той ориентацией детектора, при которой отмечается наибольшее количество частиц из всего используемого набора.

Вследствие связи между спином и его магнитным моментом внешнее магнитное поле будет приводить к прецессии спина вдоль магнитного поля. Этот эффект аналогичен классическому гироскопическому эффекту – магнитное поле действует на магнитный дипольный момент и создаёт крутящий момент, который прикладывается к спиновому механическому моменту частицы и приводит к прецессии оси вращения и спина частицы.

В квантовой механике спин описывается не просто вектором как классический момент импульса, а с помощью математических объектов – спиноров. Поведение векторов и спиноров при вращении координат различается. Например, каждое вращение частицы со спином 1/2 на 360 градусов приводит частицу не в прежнее состояние, а в состояние с противоположной квантовомеханической фазой. Для частицы с нулевым спином её квантовое состояние при вращении не меняется. Если же у частицы спин равен 2, то при вращении на 180 градусов она получает прежнее квантовое состояние.

Математическая формулировка спина в квантовой механике

Оператор спина

Оператор спина подчиняется тем же соотношениям, что и оператор орбитального момента импульса:

$[S_i, S_j ] = i \hbar \epsilon_{ijk} S_k$

где $ε ijk$ – символ Леви-Чивиты. Собственные векторы операторов $S 2$ и $S z$ (выраженные через кет-векторы в общем $S$ -базисе) равны:

$S^2 |s,m\rangle = \hbar^2 s(s + 1) |s,m\rangle,$

$S_z |s,m\rangle = \hbar m |s,m\rangle,$

где через $m$ обозначено квантовое число проекции спина на выделенную ось.

Операторы увеличения и уменьшения спина, действующие на данные собственные векторы, дают соотношения:

$S_\pm |s,m\rangle = \hbar\sqrt{s(s+1)-m(m\pm 1)} |s,m\pm 1 \rangle$ , где $S_\pm = S_x \pm i S_y.$

В отличие от орбитального момента импульса, указанные собственные векторы (и соответствующие матричные элементы) не выражаются через сферические гармоники и не являются функциями углов $θ$ и $φ$ . Величины s и m могут быть полуцелыми числами.

В квантовой механике спин квантуется в единицах постоянной Дирака $~{\hbar}$ , которая образуется путём деления постоянной Планка (постоянной действия) на $2π$ . При этом функция состояния частицы $\psi =\psi(\mathbf r,\sigma)\,$ зависит как от координат в виде радиус-вектора $\mathbf r$ , так и от $~\sigma$ в виде дискретного набора величин:

$\sigma \in \{-s\cdot\hbar , -(s-1)\cdot\hbar , ... ,+(s-1)\cdot\hbar ,+s\cdot\hbar\}.$

Здесь можно выделить бозоны (s = 0 или 1 или 2 или ...) и фермионы (s = 1/2 или 3/2 или 5/2 или ...). В процессах взаимодействия сохраняется общий момент импульса системы, складывающийся из орбитального момента импульса и спина.

Спин и принцип запрета Паули

Для систем из N идентичных частиц действует принцип Паули, который устанавливает, что перестановка между любыми двумя из N частиц может привести к изменению волновой функции системы:

$\psi ( \,...\, ;\,\mathbf r_i,\sigma_i\,;\, ...\,;\mathbf r_j,\sigma_j\,;\,...) =(-1)^{2s}\cdot \psi ( \,...\, ;\,\mathbf r_j,\sigma_j\,;\, ...\,;\mathbf r_i,\sigma_i\,;\,...)\,.$

Для бозонов фактор $($ $- 1) 2 s$ равен +1, а для фермионов равен –1. В квантовой механике все частицы разделяются на бозоны и фермионы. В релятивистской квантовополевой теории суперсимметрии допускаются частицы, имеющие и бозонные и фермионные компоненты.

Электроны являются фермионами с величиной s = 1/2; кванты света ( фотоны) являются бозонами с величиной s = 1. Фотоны являются релятивистскими объектами и хорошо вписываются в релятивистскую квантовую электродинамику. Однако полуцелые квантовые числа для спина фермионов отличаются от целых квантовых чисел для орбитального момента и для бозонов, приводя к затруднению при классическом объяснении спина.

Спин и вращения системы координат

Согласно квантовой механике проекция момента импульса на выделенную ось квантуется, образуя ряд дискретный значений. В связи с этим наиболее подходящим квантовомеханическим способом описания спина частицы являются комплексные числа, соответствующие амплитудам вероятности нахождения заданной величины проекции спина на выделенную ось. Например, для частицы со спином 1/2 требуется два числа $a_{\pm 1/2}$ , задающие амплитуды вероятности нахождения проекций спина, равных $\hbar/2$ и $-\hbar/2$ , и удовлетворяющие условию:

$|a_{1/2}|^2 + |a_{-1/2}|^2 \, = 1.$

Поскольку эти числа зависят от выбора осей координат, при вращении осей они должны преобразовываться соответствующим образом. Из линейности преобразований, которые описываются матрицей вращения, результат последовательного вращения, представляемого двумя матрицами A и B, должен быть равен с точностью до фазы результату вращения, представляемого матрицей AB. Кроме этого, вращения сохраняют квантовомеханическое произведение, задающее матрицы преобразования:

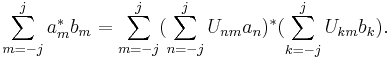
$\sum_{m=-j}^{j} a_m^* b_m = \sum_{m=-j}^{j} (\sum_{n=-j}^j U_{nm} a_n)^* (\sum_{k=-j}^j U_{km} b_k).$

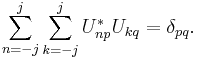
$\sum_{n=-j}^j \sum_{k=-j}^j U_{np}^* U_{kq} = \delta_{pq}.$

С точки зрения математики, эти матрицы определяют унитарное проективное представление группы вращения SO(3). Каждое такое представление соответствует представлению покрывающей группы для SO(3), которым является SU(2). Имеется одно n-мерное неприводимое представление SU(2) для каждого измерения, причём это представление является n-мерным действительным для нечётных n и n-мерным комплексным для чётных n (следовательно будет 2n действительное представление). В частности, если у частиц спин 1/2, то при вращениях он трансформируется согласно 2-мерному представлению, которое генерируется матрицами Паули:

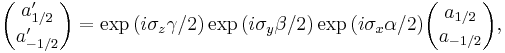
$\begin{pmatrix} a_{1/2}' \\ a_{-1/2}' \end{pmatrix} = \exp{(i \sigma_z \gamma / 2)} \exp{(i \sigma_y \beta / 2)} \exp{(i \sigma_x \alpha / 2)} \begin{pmatrix} a_{1/2} \\ a_{-1/2} \end{pmatrix},$

где $α, β, γ$ являются углами Эйлера.

При наличии у частиц более высоких спинов 1 и 3/2 они трансформируются аналогичным образом с помощью многомерных представлений и соответствующих матриц вращения.

Спин и лоренцевские преобразования

При попытке использовать аналогичный указанному выше подход для поведения спина при преобразованиях Лоренца возникает препятствие. Оно связано с тем, что в отличие от группы преобразований вращения SO(3), группа лоренцевских преобразований SO(3,1) не является компактной и не имеет необходимого унитарного ограниченно-мерного представления.

В случае частиц со спином 1/2 можно найти конструкцию, которая включает ограниченно-мерное представление и скалярное произведение, соответствующее этому представлению. Каждой частице можно приписать 4-компонентный спинор Дирака $ψ$ . Такие спиноры преобразуются при преобразованиях Лоренца по следующему закону:

$\psi' = \exp{\left(\frac{1}{8} \omega_{\mu\nu} [\gamma_{\mu}, \gamma_{\nu}]\right)} \psi,$

где $γ μ$ есть гамма-матрицы, $ω μν$ – антисимметричные 4x4 матрицы, параметризующие преобразование. При этом сохраняется следующее скалярное произведение:

$\langle\psi|\phi\rangle = \bar{\psi}\phi = \psi^{\dagger}\gamma_0\phi.$

Матрицы Паули и операторы спина

Квантовомеханические операторы, связанные со спиновыми наблюдаемыми величинами, имеют вид:

$S_x = {\hbar \over 2} \sigma_x ,$

$S_y = {\hbar \over 2} \sigma_y ,$

$S_z = {\hbar \over 2} \sigma_z .$

В особом случае спина 1/2 имеются три матрицы Паули $σ x$ , $σ y$ и $σ z$ :

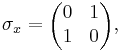
$\sigma_x = \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix} ,$

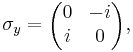
$\sigma_y = \begin{pmatrix} 0&-i\\ i&0 \end{pmatrix},$

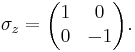
$\sigma_z = \begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix}.$

Измерение спина вдоль осей x, y, z

Каждая из эрмитовых матриц Паули имеет два собственных значения, +1 и -1. Соответствующими нормализованными волновыми собственными векторами являются следующие:

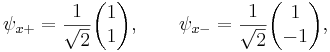
$\psi_{x+} = \frac{1}{\sqrt{2}} \begin{pmatrix} {1}\\{1}\end{pmatrix},\qquad \psi_{x-} = \frac{1}{\sqrt{2}} \begin{pmatrix} {1}\\{-1}\end{pmatrix},$

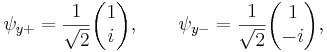
$\psi_{y+} = \frac{1}{\sqrt{2}} \begin{pmatrix} {1}\\{i}\end{pmatrix}, \qquad \psi_{y-} = \frac{1}{\sqrt{2}} \begin{pmatrix} {1}\\{-i}\end{pmatrix},$

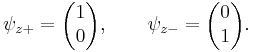
$\psi_{z+} = \begin{pmatrix} 1\\0\end{pmatrix}, \qquad \psi_{z-} = \begin{pmatrix} 0\\1\end{pmatrix}.$

Согласно постулатам квантовой механики, эксперимент, направленный на измерение компонент электронного спина вдоль осей x, y или z может дать только собственные значения спинового оператора ( $S x$ , $S y$ , $S z$ ) на эти оси, равные ${\hbar \over 2}$ и ${-\hbar \over 2}$ . Квантовое состояние частицы с учётом спина может быть представлено двухкомпонентным спинором:

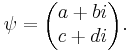
$\psi = \begin{pmatrix} {a+bi}\\{c+di}\end{pmatrix}.$

Когда спин измеряется по отношению к заданной оси, например оси x, вероятность, что измерение даст значение ${\hbar \over 2}$ , равна $\mid \langle \psi \mid \psi_{x+} \rangle \mid ^2$ . Соответственно, вероятность того, что при измерении будет получено значение ${-\hbar \over 2}$ , равна $\mid \langle \psi \mid \psi_{x-} \rangle \mid ^2$ . В ходе измерения спина спиновое состояние частицы в виде волновой функции редуцируется так, что получается какое-либо собственное состояние. В результате, если при измерении вдоль заданной оси получилось собственное значение, то и последующие аналогичные измерения вдоль этой оси не изменят результата (так как $\mid \langle \psi_{x+} \mid \psi_{x+} \rangle \mid ^2 = 1$ , и т.д.).

Измерения спина вдоль произвольной оси

Оператор спина вдоль произвольной оси может быть получен с помощью спиновых матриц Паули. Допустим $u$ $= (u x, u y, u z)$ есть произвольный единичный вектор. Тогда оператор спина в этом направлении определяется выражением $S_u = \hbar(u_x\sigma_x + u_y\sigma_y + u_z\sigma_z)/2$ . Оператор $S u$ имеет собственные значения $\pm\hbar/2$ , как и обычные спиновые матрицы. Аналогичным способом находятся операторы спина в произвольном направлении и для спинов более высокого порядка.

Нормализованный спинор для спина 1/2 в $(u x, u y, u z)$ направлении (который справедлив для всех случаев спиновых состояний, кроме состояния спин вниз, где получается 0/0), имеет вид:

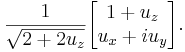
$\frac{1}{\sqrt{2+2u_z}}\begin{bmatrix} 1+u_z \\ u_x+iu_y \end{bmatrix}.$

Этот спинор получается после диагонализации $σ u$ –матрицы и определения собственных состояний и собственных значений спина.

Совместимость измерений спина

Поскольку матрицы Паули не коммутируют между собой, измерения спина вдоль осей системы отсчёта не совместны друг с другом. Это означает например, что при известном спине вдоль оси x последующее измерение спина вдоль оси y изменяет значение спина, имевшееся вдоль оси x ранее. Это видно из свойств собственных векторов (собственных состояний) матриц Паули:

$\mid \langle \psi_{x+/-} \mid \psi_{y+/-} \rangle \mid ^ 2 = \mid \langle \psi_{x+/-} \mid \psi_{z+/-} \rangle \mid ^ 2 = \mid \langle \psi_{y+/-} \mid \psi_{z+/-} \rangle \mid ^ 2 = \frac{1}{2} .$

Если при измерении спина частицы вдоль оси x получено значение ${\hbar \over 2}$ , это значит, что волновая функция спинового состояния редуцировалась в собственное состояние $\mid \psi_{x+} \rangle$ . Если затем измерять спин частицы вдоль оси y, спиновое состояние станет равным либо $\mid \psi_{y+} \rangle$ либо $\mid \psi_{y-} \rangle$ , каждое с вероятностью $\frac{1}{2}$ . Допустим, было измерено значение ${-\hbar \over 2}$ . Если теперь вернуться к измерению спина вдоль оси x, вероятность получения значения ${\hbar \over 2}$ или ${-\hbar \over 2}$ будет равна $\frac{1}{2}$ (эти вероятности равны $\mid \langle \psi_{x+} \mid \psi_{y-} \rangle \mid ^ 2$ и $\mid \langle \psi_{x-} \mid \psi_{y-} \rangle \mid ^ 2$ ). Это означает, что первоначальное значение спина вдоль оси x изменилось за счёт проведённого измерения вдоль оси y, так как вероятность получения значения спина ${\hbar \over 2}$ теперь равна только $\frac{1}{2}$ .

Использование концепции спина в науке и технике

Понятие спина широко используется в ядерном магнитном резонансе в химической спектроскопии, в электронном парамагнитном резонансе в химической и физической спектроскопии, в магниторезонансных измерениях плотности протонных спинов с целью сканирования внутренних органов в медицине, в технологиях современных компьютерных жёстких дисков на основе гигантского магниторезистивного эффекта.

Спин рассматривается как возможный носитель двоичной информации в спиновых транзисторах. Электроника, связанная с такими транзисторами, носит название спинтроника. ^[7]

Спин и принцип Паули оказываются необходимыми в квантовой механике для объяснения ряда явлений и закономерностей, таких например, как периодическая таблица Дмитрия Менделеева.

Обобщение спина

Введение спина означает применение новой физической идеи: постулирование того, что существует пространство состояний, никак не связанных с перемещением частицы в обычном пространстве. Обобщение этой идеи в ядерной физике привело к понятию изотопического спина, который действует в особом изоспиновом пространстве. В дальнейшем, при описании сильных взаимодействий были введены внутреннее цветовое пространство и квантовое число цвет, как более сложный аналог спина.

Сущность спина

Особенностью квантовой механики является то, что в ней реальные движения частиц заменяются квантованными волновыми движениями, а результаты экспериментов вычисляются в виде вероятностей тех или иных событий. Такой подход принципиально не может объяснить природу спина, поскольку для этого требуются субстанциональные модели частиц. Некоторые такие модели на основе теории бесконечной вложенности материи, а также концепция динамического спина электрона были предложены Сергеем Федосиным в 2009 г. ^[8] В теории бесконечной вложенности материи спин ряда одинаковых объектов рассматривается как собственный характерный момент импульса, которым в среднем обладают данные объекты. Если у элементарных частиц характерный спин измеряется в единицах $~\hbar$ , то на звёздном уровне материи вырожденные объекты типа нейтронных звёзд имеют характерный момент импульса порядка $\hbar_s=5,5 \cdot 10^{41}$ Дж•с (смотри звёздная постоянная Дирака). Различие спинов как характерных моментов импульса приводит к различию соотношений неопределённости на разных уровнях материи, например: ^[9]

$\Delta x \Delta p_x \geq \frac{\hbar}{2}$ для уровня элементарных частиц,

$\Delta x \Delta p_x \geq \frac{\hbar_s}{2}$ для уровня звёзд.

Одним из следствий этого становится то, что приписывание частицам, составляющим объект, того же самого значения спина, которым обладает данный объект, оказывается не всегда правильным (такая ситуация предполагается для трёх кварков внутри нуклона согласно квантовой хромодинамике и особенно в преонных моделях элементарных частиц, где в результате возникает «парадокс масс»).

Спин электрона

Основная статья: Электрон

Расчёт баланса сил на поверхности электрона с учётом действия сильной гравитации и электрической силы Кулона показывает, что электрон как самостоятельная частица не может иметь какой-то определённый радиус – электрическая сила расталкивает частицы вещества сильнее, чем сила гравитации. Стабилизация электрона в виде облака возможна в атомах, где имеются дополнительные гравитационные и электрические силы притяжения со стороны ядра, силы отталкивания от других электронов и центростремительные силы при вращении вещества.

В субстанциональной модели спин электрона носит не статическую, а динамическую природу. Он появляется за счёт сложного движения электронного облака вокруг ядра в результате взаимодействия с фотоном или другим электроном. Вещество электрона вращается вокруг центра инерции облака, давая орбитальную компоненту момента импульса. Кроме этого возникает общее вращение облака вокруг ядра атома, выражающееся во вращении центра инерции облака относительно ядра и в появлении соответствующей компоненты момента импульса. Эта компонента и является так называемым динамическим спином электрона. Она ответственна за излучение электромагнитного кванта при переходе электрона с верхнего уровня энергии на нижний, а также за спиновый магнитный момент. В отсутствие динамического спина излучение из атома стремится к нулю. Вследствие различия вращательных движений вещества, ответственных за динамический спин и орбитальное вращение, возникает различие значений g-факторов в формулах, связывающих спиновый и орбитальный моменты импульса и соответствующие им магнитные моменты.

Согласно расчётам в основном состоянии атома, а также в s-состояниях магнитный момент электрона в атоме связан не со спином (в этих состояниях динамический спин равен нулю, центр электронного облака не вращается относительно ядра), а с орбитальным вращением вещества электронного облака. Динамический спин и соответствующий ему спиновый магнитный момент для простейшего случая плоского движения вещества могут иметь два направления относительно орбитального момента электрона. Это приводит к энергии взаимодействия магнитного момента электрона и магнитного момента ядра, вращающегося относительно центра инерции электронного облака. Данная энергия приводит к расщеплению уровней энергии на дублеты в водородоподобном атоме, к мультиплетности и к тонкой структуре атомных спектров. В субстанциональной модели электрона даётся своё объяснение лэмбовскому сдвигу уровней энергии, принципу Паули, магнитомеханическим явлениям с электронами, связывающим намагничение образцов с их вращением.

Характерный спин

В ряде случаев характерный спин элементарных частиц можно найти прямым расчётом. В частности для некоторых адронов, исходя из аналогии строения их вещества с нейтронными звёздами, используется соотношение между радиусом и массой адрона: ^[10]

$~ R= R_p (\frac {M_p}{M})^{1/3} ,$

где и – радиус и масса протона.

В следующей таблице приведены массы и радиусы протона, пиона и мюона, необходимые для расчёта их спина. Радиус мюона находился с помощью теории подобия уровней материи, исходя из радиуса белого карлика, соответствующего мюону.

Характеристики протона, пиона и мюона
Частица	Масса-энергия, МэВ	Масса, 10^–27 кг	Радиус, 10^–16 м	Энергия связи , МэВ	Характерный спин, 10^–35 Дж•с	Квантовый спин
Протон p⁺	938,272029	1,6726	8,7	938,272	5,34	ħ/2
Пион π⁺	139,567	0,249	16,4	11	0,54	0
Мюон μ⁺	105,658	0,188	10900	0,095	9,1	ħ/2

Массы частиц получаются путём деления массы-энергии, переведенной из МэВ в Дж, на квадрат скорости света. Характерный момент импульса объекта находится по формуле:

$~ L_x= M C_{x} R ,$

причём характерная скорость $~ C_{x}$ частиц вещества объекта связана с абсолютной величиной полной энергии объекта в поле сильной гравитации: ^[9]

$~ W=M C^2_x= \frac { \delta \Gamma M^2}{2R} ,$

здесь $~ \delta =0,62$ для объектов типа нуклонов и нейтронных звёзд, $~ \Gamma$ – постоянная сильной гравитации.

Для протона была также найдена формула , так что для характерного спина протона получается: $~\frac {\hbar}{2}= \frac { M_p c R_p }{2 \pi}$ , где – скорость света и характерная скорость частиц вещества протона, – постоянная Планка. Если применить такой же подход для характерного спина мюона, получится следующее:

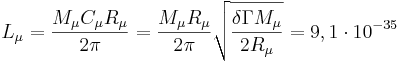$~ L_{\mu}= \frac { M_{\mu } C_{\mu } R_{\mu}} {2 \pi}=\frac { M_{\mu } R_{\mu} }{2 \pi} \sqrt{\frac {\delta \Gamma M_{\mu} }{2 R_{\mu}}}=9,1\cdot 10^{-35}$ Дж•с.

Характерный спин мюона превышает значение квантового спина ħ/2 , принятого для фермионов и лептонов. Для пиона при его радиусе согласно таблице спин получается равным 0,05 ħ , то есть значительно меньше минимального спина фермиона, равного ħ/2. Вследствие этого квантовый спин пиона полагается равным нулю, а сам пион считается бозоном. В квантовой статистике представление пиона в виде бозона существенно отличает пион от протона, являющегося фермионом. Однако пион отличается от протона лишь уменьшенной массой, так что общепринятое подразделение элементарных частиц по значению спина на фермионы и бозоны не совсем корректно в свете того, что бозонам и фермионам предписывается кардинальное различие в поведении за счёт действия принципа Паули.

Предельные соотношения для нуклонов

Можно предположить, что протон имеет не только квантовомеханический спин, равный $~\hbar/2$ , но и предельный момент импульса собственного вращения как некоторый максимальный спин. Тогда при предельном вращении возникает формула для магнитного момента протона: ^[8]

$~ P_m=0,2e \sqrt{\Gamma M_p R_p }.$

Данная формула для нейтрона несколько изменяется, поскольку в отличие от протона нейтрон в субстанциональной модели имеет более сложную внутреннюю электромагнитную структуру с неоднородным распределением электрического заряда.

Максимальный спин протона позволяет оценить его радиус путём сравнения момента импульса поля сильной гравитации и спина. ^[11]

Ссылки

B. Friedrich, D. Herschbach. Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics. Physics Today, 2003, Vol. 56, issue 12, page 53.
W. Pauli "The Connection Between Spin and Statistics", Phys. Rev. 58, 716-722 (1940), pdf.
W.J. Marciano, A.I. Sanda. Exotic decays of the muon and heavy leptons in gauge theories. Physics Letters, 1977, Vol. B67, issue 3, page 303–305.
B.W. Lee, R.E. Shrock. Natural suppression of symmetry violation in gauge theories: Muon- and electron-lepton-number nonconservation. Physical Review, 1977, Vol. D16, issue 5, page 1444–1473.
K. Fujikawa, R. E. Shrock. Magnetic Moment of a Massive Neutrino and Neutrino-Spin Rotation. Physical Review Letters, 1980, Vol. 45, issue 12, page 963–966.
N.F. Bell et al. How Magnetic is the Dirac Neutrino? Physical Review Letters, 2005, Vol. 95, issue 15, page 151802. arXiv hep-ph/0504134.
Spintronics. Feature Article в Scientific American, June 2002.
Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
Федосин С. Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1, 544 стр., Табл.66, Ил.93, Библ. 377 назв.
Комментарии к книге: Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
Федосин С.Г. Современные проблемы физики. В поисках новых принципов, М: Эдиториал УРСС, 2002, ISBN 5-8360-0435-8, 192 стр., Ил.26, Библ. 50 назв.

Справочная литература

"Физическая энциклопедия" под ред. Прохорова А.М. -М.: Научное издательство "Большая российская энциклопедия".-1994 г. ISBN 5-85270-087-8.