Advances in Physics Theories and Applications, 2013,
Vol. 23, P. 19 – 25.
4/3 problem
for the gravitational field
Sergey G. Fedosin
PO
box 614088, Sviazeva str. 22-79, Perm, Russia
E-mail: intelli@list.ru
Abstract
The
gravitational field potentials outside and inside a uniform massive ball were
determined using the superposition principle, the method of retarded potentials
and Lorentz transformations. The gravitational field strength, the torsion
field, the energy and the momentum of the field, as well as the effective
masses associated with the field energy and its momentum were calculated. It
was shown that 4/3 problem existed for the gravitational field as well as in
the case of the electromagnetic field.
Keywords: energy, momentum, theory of relativity,
gravitation, field potentials
1. Introduction
In field theory, there are a number of unsolved
problems, which need deeper analysis and logical understanding. An example is
the problem of choosing a universal form of the stress-energy tensor of the
body, which would include the rest energy of the substance as well as the field
energy and at the same time
would provide an univocal connection with thermodynamic variables of the
substance in the language of four-vectors and tensors. Another interesting
problem is 4/3 problem, according to which the effective mass of the body
field, which is calculated through the field momentum, and the effective mass
of the field, found through the field energy, for some reason do not coincide
with each other, with the ratio of the masses approximately equal to 4/3.
The problem of 4/3 is known for a long
time for the mass of electromagnetic field of a moving charge. Joseph John Thomson, George Francis FitzGerald,
Oliver Heaviside, George Frederick Charles Searle and many others write about
it (Heaviside 1888/1894), (Searle 1897), (Hajra 1991). We also
discuss this question with respect to the gravitational field of a moving ball
(Fedosin 2008). Now we present a more accurate description of the problem, not
limited to the approximation of small velocities.
2. Methods
In
the calculation of the energy and the momentum of gravitational field of a
uniform massive ball, we will use the superposition principle by means of
summing up the field energies and momenta from all point particles forming the
moving ball. This approach is reasonable in the case of a weak field, when the
general theory of relativity changes to gravitomagnetism and the covariant
theory of gravitation – to the Lorentz-invariant theory of gravitation (Fedosin 2009a).
The field equations then become linear, allowing the use of the superposition
principle. We will note that the gravitational field can be considered weak if
the spacetime metric differs insignificantly from the Minkowski spacetime
metric (the spacetime metric of the special theory of relativity). If the
effects of gravitational time dilation and sizes contraction are significantly
less than the similar effects due to the motion velocity of the reference frame
under consideration, then this gravitational field can be considered weak.
3. Results and Discussions
3.1 The Gravitational Field Outside a Uniform Massive Ball
We
will first define the gravitational field potentials for a ball moving at a
constant velocity 
along the
axis 
of the
reference frame 
. We will proceed from the so-called Liénard-Wiechert potentials (Liénard
1898; Wiechert 1900) for any point particles that
make up the ball. Popular presentation of the problem (for the electromagnetic
field) can be found in Feynman’s book (Feynman at all. 1964). Similarly to
this, the differential scalar Liénard-Wiechert
potential for the gravitational field from a point particle with mass 
has the
following form:
, (1)
Where
is the
gravitational constant, 
is the
velocity of gravitation propagation, vector 
is the
vector connecting the early position of the point particle at time 
and the
position 
at which
the potential is determined at time 
. In this case, the equation must hold:
. (2)
The
meaning of equation (2) is that during the time period 
the
gravitational effect of the mass must cover
the distance 
at
velocity 
up to the
position 
so that at
this position the potential 
would
appear.
Suppose
there is continuous distribution of point particles and at 
these
particles are described by the coordinates 
and the center of distribution of point particles coincides with
the origin of the reference frame. Then at time the
distribution center of the point particles would move
along the axis to the position 
, and the radius vector of an arbitrary particle
of distribution would equal 
. At the early time 
the
position of this point particle is specified by the vector 
. Since 
and 
according
to (2), then for the square 
we can
write down:
. (3)
The
right side of (3) is a quadratic equation for the time . After we find from (3),
we can then find from (2).
If we consider that in (1) the product of vectors is 
, then substituting also in
(1), we obtain the following expression (Fedosin 2009b):
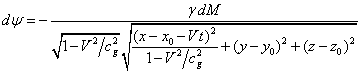. (4)
According
to (4), the differential gravitational potential of the
point mass at the
time during its
motion along the axis depends on
the initial position of this
mass at . If we use the extended Lorentz transformations
for the spatial coordinates in (4):
, 
,
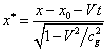, (5)
and then let the velocity 
tend to
zero, we obtain the formula for the potential in the reference frame 
the origin
of which coincides with the point mass :
. (6)
In
(6) in the reference frame the vector
at the
proper time 
specifies
the same point in space as the vector in the
reference frame at the time . If we introduce the gravitational four-potential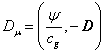 
, including the scalar potential 
and the
vector potential 
(Fedosin 1999),
then
the relation between the scalar potential (6) in the reference frame and the
scalar potential (4) in the reference frame 
can be
considered as the consequence of extended Lorentz transformations in
four-dimensional formalism, which are applied to the differential
four-potential of a single point particle. These transformations are carried
out by multiplying the corresponding transformation matrix by the
four-potential, which gives the four-potential in a different reference frame
with its own coordinates and time.
Since
in the reference frame the point
mass is at rest, its vector potential is 
, and the four-potential has the form: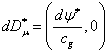 
.
In
order to move to the reference frame , in which the reference frame is moving
at the constant velocity along the
axis , we must use the matrix of inverse partial Lorentz
transformation (Fedosin
2009a):
,
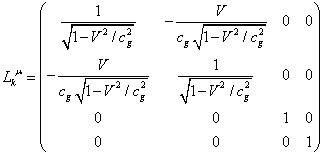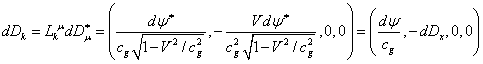. (7)
From
(7) taking into account (6) and (5) we obtain the following relations:
,
,
,
. (8)
The
first equation in (8) coincides with (4) and the differential vector potential
of the point mass is directed along its motion velocity.
After
integration of (8) over all point masses inside the ball on the basis of the
principle of superposition, the standard formulas are obtained for the
potentials of gravitational field around the moving ball, with retardation of
the gravitational interaction taken into account:
, 
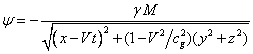, (9)
Where – the scalar potential of the moving ball, 
– the mass of the ball, 
– the coordinates of the
point at which the potential is determined at the time (on the condition that the center
of the ball at 
was in the origin of coordinate system),
– the vector potential of the ball.
In (9) it is assumed that the ball is
moving along the axis 
at a constant speed , so that 
, 
, 
. With the help of the field
potentials we can calculate the field strengths around the ball by the formulas
(Fedosin 1999):
, 
, (10)
Where 
is the gravitational field strength, 
–
the gravitational torsion in Lorentz-invariant theory
of gravitation (gravitomagnetic field in gravitomagnetism).
In view of (9) and (10) we find:
,
,
, 
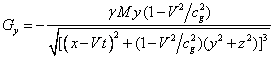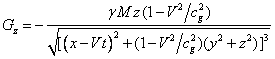, (11)
,
.
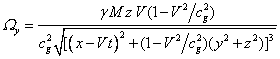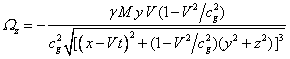The energy density of the gravitational
field is determined by the formula (Fedosin 1999):
.
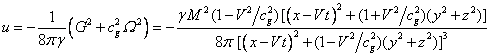(12)
The total energy of the field outside the
ball at a constant velocity should not depend on time. So it is possible to
integrate the energy density of the field (12) over the external space volume at . For this purpose we shall introduce new coordinates:
, 
, 
. (13)
The
volume element is determined by the formula 
, where 
is
determinant of Jacobian matrix:
.
It follows that 
. The integral over the space of the energy
density (12) will equal:
.
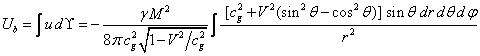(14)
We shall take into account that due to the
Lorentz contraction during the motion along the axis the ball must be as
Heaviside ellipsoid, the surface equation of which at is the following:
. (15)
After substituting (13) in (15), it
becomes apparent that the radius 
at the integration in (14) must change from 
to 
, and the angles 
and 
change the same way as in spherical
coordinates (from 0 to 
for the angle , and from 0 to 
for the angle ). For the energy of the
gravitational field outside the moving ball we find:
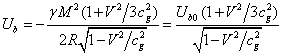, (16)
Where 
is the field energy around the stationary ball.
We can introduce the effective
relativistic mass of the field related to the energy of moving ball:
. (17)
We shall now consider the momentum density
of the gravitational field:
, (18)
Where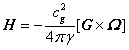 
is the vector of energy flux density of the
gravitational field (Heaviside vector) (Fedosin 1999).
Substituting in (18) the components of the
field (11), we find:
,
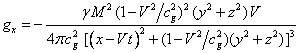(19)
,
.
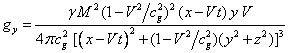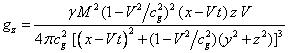We can see that the components of the
momentum density of gravitational field (19) look the same as if a liquid
flowed around the ball from the axis , carrying similar density of the momentum – liquid
spreads out to the sides when meeting with the ball and merges once again on
the opposite side of the ball. Integrating the components of the momentum
density of the gravitational field (19) by volume outside the moving ball at as in (14), we obtain:
.
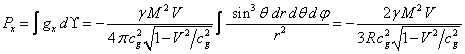(20)
, 
.
In (20) the total momentum of the field
has only the component along the axis . By analogy with the formula for
relativistic momentum the coefficient before the velocity in (20) can be interpreted as the effective
mass of the external gravitational field moving with the ball:
,
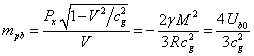(21)
Where 
is the energy of the external static field of
the ball at rest.
Comparing (21) and (17) gives:
. (22)
The discrepancy between the masses 
and 
in (22) shows the existence of the problem of
4/3 for gravitational field in the Lorentz-invariant theory of gravitation.
3.2 The Gravitational
Field Inside a Moving Ball
For
a homogeneous ball with the density of substance 
(measured
in the comoving frame), which is moving along the axis , the potentials inside the ball (denoted by
subscript i ) depend on time and are as follows (Fedosin 2009b):
,
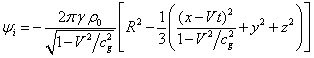. (23)
In view of (10) we can
calculate the internal field strength and torsion field:
, 
, 
,
, 
, 
.
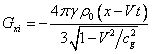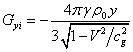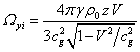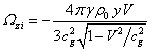(24)
Similarly to (12) for the energy density
of the field we find:
.
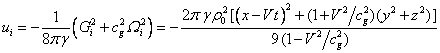(25)
According to (25) the minimum energy
density inside a moving ball is achieved on its surface, and in the center at it is zero.
The integral of (25) by volume of the ball
at in coordinates (13) with the volume element equals:
.
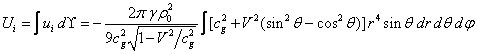(26)
According to the theory of relativity the
moving ball looks like Heaviside ellipsoid with equation of the surface (15) at , and in the coordinates (13) the
radius in the integration in (26) varies from 0 to. With this in mind for the energy of
the gravitational field inside the moving ball, we have:
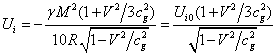, (27)
Where 
is the field energy inside a stationary ball
with radius .
The effective mass of the field associated
with energy (27) is:
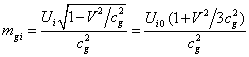. (28)
Substituting in (18) the components of the
field strengths (24), we find the components of the vector of momentum density of gravitational field:
,
,
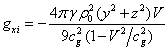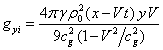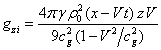. (29)
The vector connecting the origin of
coordinate system and center of the ball depends on the time and has the components 
. From this in the point, coinciding
with the center of the ball, the components of the vector of the momentum
density of the gravitational field are always zero. At the center of the ball passes through the
origin of the coordinate system, and at the time from (29) it follows that the
maximum density of the field momentum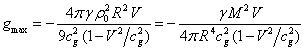 
is achieved on the surface of the ball on the
circle of radius in the plane 
,
which is perpendicular to the line of the ball’s motion. The same follows from
(19).
We can integrate the components of the
momentum density of gravitational field (29) over the volume inside the moving
ball at in the coordinates (13) similar to (20):
.
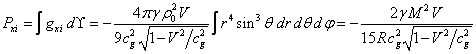(30)
, 
.
As in (20), the total momentum of the
field (30) has only the component along the axis . By analogy with (21) the
coefficient before the velocity in (30) is interpreted as the effective mass of
the gravitational field inside the ball:
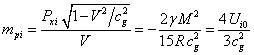, (31)
Where is the field energy inside a stationary ball.
Comparing (28) and (31) gives:
. (32)
Connection (32) between the masses of the field inside the ball is the
same as in (22) for the masses of the external field, so the problem of 4/3
exists inside the ball too.
4. Conclusion
A characteristic feature of the fundamental
fields, which include the gravitational and electromagnetic fields, is the
similarity of their equations for the potentials and the field strengths. As
it was shown above, the external potentials (9) of the gravitational (and
similarly, the electromagnetic) field of the moving ball are similar by their
form to the potentials of the point mass (point charge) (8), and can be
obtained both using the superposition principle of potentials of the point
masses inside the ball, and using the Lorentz transformation. We also presented
the exact field potentials (23) inside the moving ball, for which both the
superposition principle and the Lorentz transformation are satisfied.
From
the stated above we saw that the 4/3 problem was common for both the
electromagnetic and the gravitational field. It also followed from this that
considering the contribution of the energy and the momentum of both fields into
the mass of the moving body were to be done in the same way, taking into
account the negative values of the energy and the momentum of gravitational
field and the positive values of the energy and the momentum of electromagnetic
field.
REFERENCES
1.
Fedosin SG (1999). Fizika i
filosofiia podobiia: ot preonov
do metagalaktik, Style-MG, Perm.
2. Fedosin SG (2008). Mass,
Momentum and Energy of Gravitational Field, Journal of Vectorial Relativity,
3 (3): 30-35.
3. Fedosin SG
(2009a). Fizicheskie teorii i beskonechnaia vlozhennost’ materii,
Perm.
4. Fedosin SG
(2009b). Comments to the book:
Fizicheskie teorii i beskonechnaia vlozhennost’ materii, Perm.
5. Feynman RP, Leighton R, Sands M (1964). The Feynman
lectures on physics. Vol. 2. Addison-Wesley, Massachussets.
6.
Hajra S
(1991). Classical Electrodynamics – Reexamined, Indian Journal of Theoretical
Physics, 42 (2): 164.
7.
Heaviside O (1888/1894). Electromagnetic
waves, the propagation of potential, and the electromagnetic effects of a
moving charge, Electrical papers, 2:
490-499.
8.
Liénard AM (1898). Champ électrique et
Magnétique, L’éclairage électrique, 16
(27-29): 5-14, 53-59, 106-112.
9. Searle GFC (1897). On the steady motion of
an electrified ellipsoid, The Philosophical Magazine Series 5, 44 (269):
329-341.
10.
Wiechert E (1900). Elektrodynamische Elementargesetze, Archives Néerlandaises, 5: 549-573.
Source:
http://sergf.ru/pgen.htm