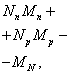Caspian
Journal of Applied Sciences Research, 2012, Vol. 1, No 13, P. 1 – 15.
The
Principle of Proportionality of Mass and Energy: New Version
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
The essence of mass and its relation
to the relativistic energy is considered. It is assumed that the rest energy is
equal to the total binding energy of the body and can be found through the
energies of fundamental fields associated with the substance of the body. Mass
as a measure of inertia is calculated by relativistic energy and relativistic
momentum. The conclusion is made that after radiation of energy from a system
the mass of the system must not decrease, but increase. The opposite case is
heating of bodies by external sources, which must be accompanied by an increase
in entropy and decrease in the mass of the bodies. On the basis of strong
gravitation mass defect of atomic nuclei is explained. Conclusions of the
general theory of relativity and the covariant theory of gravitation with
respect to the mass and energy of gravitational field are opposite – in the
general theory of relativity, relativistic energy and mass of a body are
reduced by the mass-energy of its own gravitational field, and in the covariant
theory of gravitation the mass-energy of the gravitational field increases the
relativistic energy and body mass.
Keywords: mass; energy; principle of
equivalence; tensor of entropy; mass defect.
PACS:
03.20.+i, 04.20 -q, 05.70.-a, 21.10 Dr
Knowledge of the essence of mass and energy, as well
as ways of defining them, are one of the most important problems in physics.
This is due to extensive use of the law of conservation of energy and momentum
in various areas and due to the possibility of calculating the acting forces
through the energy gradients in spacetime. The relationship between mass and
energy should be the most simple in the frame of reference in which the body
rests and does not rotate, since the momentum and the angular momentum of the
body are equal to zero and the kinetic energy of linear motion of the body as a
whole and the rotational energy do not participate in the calculation of the
mass.
Studying the relationship of mass and energy of a body
at rest during the formation of the theory of relativity led to the relation:
,
(1)
where 
– the
relativistic energy at rest ,
– the body
mass,
– the
speed of light.
Initially it was considered that the coefficient 
in (1) is
sufficiently close to 1, then by the efforts of O. Heaviside (1889) [1], A.
Poincare (1900) [2], A. Einstein (1905) [3] and a number of other physicists it
was established that 
.
From (1) it does not follow that the mass and the
relativistic rest energy are synonyms, the designation of the same. On the one
hand, the body mass is an integral property that determines the inertia of the
body upon receipt of acceleration from a force. Integrality here means that not
only substance of the body makes contribution to the mass but also physical
fields associated with this substance, as well as fields from external sources
in the body volume. On the other hand, the energy is associated more with the
law of conservation of energy, with the ability to transfer of energy from one
place to another in different ways and in different forms, such as heat
transfer, electromagnetic radiation, electricity, etc. The force 
, acting on the body, is defined as the rate of
change of momentum, and the mass is directly included in the momentum 
as a
factor. When calculating the force in external field the formula is often used
in which the force is the gradient of potential energy 
of the
body, taken with opposite sign. This implies the following:
.
(2)
It is seen from (2) that although all forms of energy
are contributing to the body mass (and hence to the momentum), but the force as
the rate of change of momentum can only depend on the gradients of certain
energies. If we take the average over the entire volume, the energies without
gradients and energy fluxes do not cause force and acceleration, although they
are involved in formation of the body mass. In this connection it must be
assumed that the mass represents the static integral gravitational and inertial
properties of the body, appearing as a result of energy fluxes that interact
with the body.
As it was described in [3] the body mass emitting some
energy 
in the
form of two oppositely directed photons, should be reduced by the amount 
. To verify this conclusion, we once again repeat
the thought experiment with the body, which emits photons. In this case we
shall use the formulas for relativistic energy and momentum from [4]:
, 
, 
, (3)
where is a
positive value for the relativistic energy of a body at rest,
is the
total energy of particles of the body at the atomic level, which includes
various types of energies associated with atoms and molecules near absolute zero
temperature: the energy of strong interaction, which bounds the substance of
elementary particles and retains the nucleons in atomic nuclei; the energy of
electromagnetic interaction of particles; the energy of motion of substance
inside the nucleons and the energy of the nucleons in nuclei and the electrons
in atoms; the rotational energy of atoms and molecules; the vibrational energy
of atoms in molecules, etc.,
is the total energy of the body
at the macro level, taking into account the internal kinetic energy 
in the form of kinetic energy of
chaotic motion of atoms and molecules and the energy of the turbulent motion of
substance fluxes, as well as the energies of the fundamental macroscopic
fields.
The sum 
is the internal energy of a
system, commonly used in thermodynamics in the weak-field interaction between
the particles of the system. According to (3), the relativistic energy is
binding energy of the body, or the total energy taken with the negative sign.
By definition, the total macroscopic energy can be divided into three
components:
,
(4)
where 
and 
are the energies
of macroscopic gravitational and electromagnetic fields in the substance of the
body, respectively, calculated inside the body and outside of it. In the same
energies the energies of fields from external sources should be included that
fall inside the body and change the energy of the substance.
We shall take into account in (4) the virial theorem, according to which
the absolute value of the potential energy of fields is on the average twice as
much than the internal kinetic energy for bodies that are only under action
their proper gravitational and electromagnetic fields:
, 
. (5)
For the energy similarly to (5) it can be written down:
, (6)
where 
is the
total energy of the field of strong gravitation, which is assumed at the level
of elementary particles and atoms, and instead of strong interaction holds the
substance of nucleons and the nucleons in atomic nuclei, as well as is one of
the components that holds electrons in their orbits in atoms,
– is the
electromagnetic energy in the substance of elementary particles and around them
in atoms.
Taking into account (5) and (6) the relativistic
energy (3) of a body at rest can be written down as follows:
. (7)
The main contribution to the energy is made by
the negative energy of the
field of strong gravitation, which provides the positivity of the relativistic energy
and the body mass, determined by the expression:
.
(8)
We shall pass now to the thought experiment. We shall
suppose there is a body at rest and two photons are emitted from the body in
opposite directions, one photon with the energy 
along the
axis 
, and the other with the same energy against the
axis . We shall assume that the photon emission occurs
only due to changes in the energy of macroscopic fields, then the energy
balance before and after the emission has the form:
. (9)
After the emission the body remains stationary, since
the momenta of the photons are opposite and the total momentum of the system
remains zero. It is assumed in (9) that at the moment of emission the
components of the energy are
changed, and the energy of photons is taken with the minus sign, which means
the body's energy loss due to emission. It follows that 
, and hence 
. Both energies 
and 
are
negative, so that for the absolute values of energy we obtain: 
. Relation (9) also shows that the relativistic
energy 
is greater
than the energy .This entails an increase in the body mass after
the emission of photons: 
. Such result conforms to the fact that the more
energy a star radiates, the more this star is compressed and heated. The total
energy of such
star becomes more negative and the positive internal kinetic energy in (5)
increases, which according to (7) and (8) increases the mass of the star. One
of the reasons for choosing the negative sign before in (7) is
the symmetry of this expression when 
has the
negative sign too. In addition, the energy of gravitation in the compression of
the star is converted into the internal kinetic energy and the radiation
energy, and according to virial theorem these energies are approximately equal
to each other. If the energy of gravitation generates the radiation energy, in
the same degree the energy of gravitation can generate the additional
relativistic energy and mass of the star. In this case, the system star +
universe obeys the law of energy conservation – the negative change of the
gravitational energy in the compression of the star is compensated by a
positive change in the internal energy of the substance and the appearance of
the radiation energy from the star.
In principle, electromagnetic radiation and photon
emission are impossible, if no work is done on the electric charges. If a
charge is accelerated by the gravitational force, the work of gravitation will
increase the energy of the system with transfer of some energy to radiation
from the charge. In betatron the work of the magnetic field is converted into
acceleration of electrons producing synchrotron emission. In atom, the strong
gravitation and the electric field of the nucleus do work on the electron in
its transition from one energy state to another, which leads to emission from
the atom. In all cases, the work performed exceeds the energy of radiation,
which makes it possible to increase the relativistic energy of radiating system
at the time of radiation.
The described above grounds for (9) and for choosing
the negative sign before the photon energy 
are
missing in [3]. Instead of it the mechanical model of the phenomenon is
considered, when the photons as some parts of the body leave the body and take
away part of its mass. Accordingly, in this picture the positive sign of the
photon energy is chosen, and the body mass after the emission of photons should
decrease. However, the photons are not part of the body because they are
generated due to absolute acceleration of charges of the body without decrease
in the magnitude of these charges (if the body mass can vary due to changes in
the body's energy, then the charge of the body remains until the moment when it
will removed from the body or compensated by a charge of the opposite sign).
Therefore, the loss of the relativistic energy of the body due to the transfer
of photon energy must be compensated by an increase rather than decrease in the
energy and the body mass.
We shall now consider the photon emission from the
body moving at the velocity 
along the
axis . The photon emitted in the direction of the axis
, will have blue shift of its wavelength and the increased
energy, and the photon emitted in the opposite direction, will have red shift
of the wavelength and the decreased energy. The total energy of both photons
according to formula for the Doppler effect will be equal to 
, and the total momentum of the photons is equal
to 
and is
directed along the velocity of the body.
Taking into account the formulas (3), the balance of
energies and momenta before and after the photon emission gives the following:
,
. (10)
In (10) the energy and momentum of photons have the
minus sign, since the photons carry away from the body some part of its energy
and momentum. In the moment of photon emission a corresponding increase in body
mass, relativistic energy and momentum takes place. After canceling the
identical terms (10) turns into (9). This means that the difference between the
formulas for the processes of photon emission of the body at rest and the body
in motion is associated only with the Lorentz transformation and is determined
by the factor 
.
Heating
of bodies
From the above we can come to the idea that heating of
a body by the external sources of energy should decrease the body mass. As it
was found in [5] based on Lorentz-invariant thermodynamics, the amount of heat 
, that is appeared in a certain volume 
of the
body during the time 
, is determined by the integral:
, (11)
where 
is the
density of the flux of gravitational energy,
– the electromagnetic
energy flux density (the Poynting vector),
– the unit
vector of the normal to the surface area 
surrounding the volume .
According to (11), the increase in the heat can be
described by the incoming fluxes of energy of the fundamental fields – either
by the integral of the divergences of energy fluxes over volume or by using the
Gauss theorem for the integral of the energy fluxes over the area. Equation
(11) is easier to understand if we consider the following formulas:
, 
, (12)
where 
and 
are the
energy densities of gravitational and electromagnetic fields in the form of
timelike components of the corresponding stress–energy tensors,
and 
– the
densities of mass and electric current, respectively,
and 
– the
strengths of gravitational and electromagnetic fields (gravitational
acceleration and electric strength).
If we substitute (12) in (11), we see that the heat in
volume of the body increases when the energy of field is increasing, as well as
when due to the energy of fields the work 
is done in
the unit volume per unit time. The differential of entropy is expressed by the
formula:
,
(13)
where 
is the
absolute Kelvin temperature.
According to (13), if the body is heated by the
external sources, the entropy of the body increases. If the energy is radiated
from the body in the process of gravitational contraction and heating of the
substance, the total energy of the body is reduced by and the increment
of entropy 
is
negative. This is due to the fact that although the substance under compression
and decrease in its volume is heated and the entropy of the substance
increases, but the negative entropy of the gravitational field of the body
changes even more, so that the total entropy of the substance and the field is
negative. For the entropy of a spherical body, we derived the formula [5]:
,
(14)
where the radius-vector 
is
measured from the center of the body,
– the
pressure in the comoving reference frame,
is the
function of compression, calibrated so that the energy density of the substance
at rest is equal to the value 
,
– the
density of substance at rest.
In (14) the integration is over the entire volume 
of space,
both inside and outside the body. The main contribution to the negative entropy
of the body is made by the gradient of the gravitational field energy density and the
gradient of pressure . Estimation of entropy per particle of ideal gas
in gravitationally bound ball at a constant temperature of the volume, gives
the value 
, where is the
Boltzmann constant.
As the energy is radiated from the body the entropy of
the body becomes more negative, the entropy of the outgoing radiation is positive,
in the result the total entropy of the body and the radiation is zero. This
conclusion follows from the virial theorem and from (13), in which means both
the heat content of the body as a result of its gravitational contraction, and
the energy carried away by the outgoing radiation. Zero entropy was at the
beginning of formation of the body too when the substance at infinity was at
rest and in the dispersed state.
In [6], we have derived the Lorentz covariant
expression of the first law of thermodynamics, have found the tensor function
of the chemical potential, the tensor function of the work-energy of the
system, as well as the tensor function of heat 
:
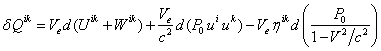, (15)
where 
is the
invariant volume of a small unit of substance or a small volume of space
occupied by the field in the absence of substance,
and 
– the
stress–energy tensors of gravitational and electromagnetic fields,
–
4-velocity of substance,
– the
metric tensor of Minkowski spacetime.
From (15) it follows that at constant volume of the
substance unit the increment of heat occurs from the increments of the density
of energy-momentum of fields and changes of the internal pressure 
, depending on the 4-velocity for an outside
observer. All terms listed in (15) can directly increase the kinetic
temperature of the substance unit and therefore are part of . To obtain the amount of heat of the body as a
set of the substance units should be
summed over all volume elements. Increment of entropy tensor is defined as in
(13):
.
Symmetric tensor of entropy is the integral over the
volume:
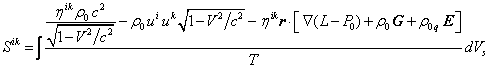, (16)
where 
is
the charge density.
For a unit of substance of gravitationally bound body
after a number of simplifications, the formula for the timelike component of
the entropy tensor is obtained:
,
where 
is the
change in the density of substance on the length of the unit of substance,
– the gas
constant, 
– the
amount of substance in moles.
We can show that not only 
, but other components of tensor 
are
negative. As it follows from (16), the entropy of the substance unit is
proportional to the ratio of the absolute value of ordered energy in this unit
and the energy of random thermal motion of particles of substance, taken with
the minus sign. Under the ordered energy we mean the energy of directional
motion of the substance unit, the energy of pressure compression and the
potential energy of the substance unit in gravitational and electromagnetic
fields. Entropy is the function of the system state, because if the system
state is set by a number of physical quantities, then in each such state, after
some relaxation time, usually only one definite relation between the ordered
and disordered system energies is carried out that is independent on the way of
transition into this state. This relation is fixed by the concept of entropy.
In the theory of infinite hierarchical nesting of
matter [6] it is supposed that the source of ordering and the ordered energy of
bodies are the fluxes of gravitons, whose properties are similar to those of
photons and neutrinos, as well as high-energy charged particles. These field
quanta and particles, appearing at lower levels of matter, due to their
relatively high energy in comparison with their mass, have the highest ordering
in our world and carry it in the space.
The stream of ordering is received by a gravitational
system with a flux of gravitons, and it generates negentropy in the system, as
the flux of gravitons outgoing from the system has lower temperature with
nearly the same energy as the energy of the incoming flux of gravitons. This
negentropy allows reducing the entropy of the system to negative values. In
addition, the outgoing emission from the system, typically electromagnetic, has
its proper entropy, so that approximately one half of the negentropy of the
fluxes of gravitons is spent on the system entropy loss due to outgoing
emission.
In accordance with the above-mentioned and [4], we
assume that the observed heating of an object due to gravitational contraction
leads to an increase in mass of the object. This process is accompanied by the
emission of photons from the object with total energy equal to the relativistic
energy of the object, excluding the rest energy, and is equal to the absolute
value of the total macroscopic energy (macroscopic binding energy). At the same
time the total energy and the entropy of the object have the negative sign. In
the reverse process the external radiation heats the object and increases the
total macroscopic energy and the entropy, and hence reduces the relativistic
rest energy and the mass of the object associated with it.
Nuclear
energy
In modern physics it is supposed that for determination
of the relativistic energy of the body it is necessary to sum up the rest
energy of its constituent particles and the total energy of the body, taking
into account the mechanical energy of particles and the energy of fields. For
the fundamental forces the total energy is usually negative, so that the
relativistic energy and the body mass are less than the energy and the mass of
all particles of the body, separated from each other. In the theory of infinite
hierarchical nesting of matter, there is infinite number of levels of the
matter with objects of corresponding masses located on them. If at some basic
level of matter we take quite many objects and start putting them together into
more massive objects, then due to the negative total energy the relative mass
of objects will be less and less at each subsequent level of matter, in
relation to the total mass of the primary objects.
According to our assumptions, the total energy in the
gravitational field is included in the relativistic energy with the negative
sign, which leads not to a decrease but to an increase in the relative mass of
objects with increasing of the mass of these objects. If we consider the
question from a philosophical point of view, the conclusions about the probable
decrease or increase in the relative mass of objects as we move to higher
levels of matter seem to be equally valid. Apparently, the choice can be made
by comparison with the experimental data.
Most clearly the relationship between mass and energy
is revealed in the case of fusion of light nuclei and in the decay of massive
nuclei, when small differences in the masses of the initial and the final
reaction products are accompanied by the release of large amounts of energy. In
Table 1, according to [7], [8], the masses of some nuclei are given in
comparison with the sum of the masses of separate protons and neutrons, of
which these nuclei could be composed.
Table
1
|
Nucleus |
Number of neutrons, |
Number of protons, |
the mass of neutrons, |
the mass of protons,
|
mass of the nucleus, |
|
|
|
1 |
1 |
1.674 927 351 |
1.672 621 777 |
3.343 583 48 |
0.003 965 65 |
|
|
34 |
28 |
56.947 529 93 |
46.833 409 75 |
102.808 9 |
0.972 04 |
|
|
146 |
92 |
244.539 393 |
153.881 203 |
395.208 8 |
3.211 8 |
,
According to Table 1, the mass of any nucleus is less
than the total mass of nucleons, of which the nucleus can be formed. Mass
defect, shown in the last column of Table 1 is such that the decrease in the
mass of the nucleus can reach almost 1 %. In the standard model it is supposed
that after combining the nucleons their total mass decreases due to the
negative total energy of the nucleus. If, however, we proceed from our
assumptions, then similarly to (3) for the relativistic energy and the mass of
the nucleus at rest we should write down:
, 
,
(17)
where 
– total
energy of the free neutrons necessary for the formation of the nucleus, 
– the
total energy of the free protons that make up the nucleus, 
– the
total energy of the nucleus in the connection of nucleons, consisting of the
kinetic energy of motion and rotation of the nucleons in the nucleus, and of
the potential energy of their interaction by means of gravitational and
electromagnetic fields in accordance with the gravitational model of strong
interaction.
We shall note that in (17) we put the plus sign to the
total energy 
, in contrast to the minus sign, standing before
the total energy in (3).
This is due to the fact that after the gravitational contraction the energy of
the gravitational field is transferred in the form of radiation to the
environment, and to the heating of substance, thus creating the mass of
radiation and the additional mass, as it is seen from (3). But the situation
with formation of the atomic nucleus from nucleons is different. For the
emergence of the nucleus it is necessary either to heat up nucleons from an
external source to the temperature sufficient to initiate fusion of the nuclei,
or to do some work on the nucleons. While a system emits photons during the
gravitational contraction, then in contrast to it for nuclear fusion it is
necessary in some way to introduce some extra energy in the system. This is
similar of the effect of thermal heating described in the previous section and
in our opinion it leads to a decrease in mass of the system.
From a formal point of view, the relation (3)
describes the process of creating the mass of photons in the environment of the
system and creating the additional mass of the system in the form 
. To describe
the formation of the nucleus and the changes in its mass we can assume that the
interaction between the nucleons leads to the negative mass of photons (photons
are not generated, but on the contrary absorbed by the system; or some work is
done on the system) and to a certain total energy, taken with the minus sign.
Substitution in (3) instead of the total
energy , but taken with the minus sign, gives the change
in mass 
and the
plus sign before in (17).
Since the total energy by itself
is negative, then in (17) the mass of the nucleus 
is less
than the total mass of protons and neutrons that make up the nucleus.
How are the nucleons held in atomic nuclei? In [6] we
gave some simple models of nuclei and described nuclear forces, due to which
the nucleons in a nucleus can be in equilibrium. Similarly, in order to
substantiate the stability of some of the hadrons, in [9] we have developed
their models based on the binding of nucleons and light mesons. The solidity of
the nuclei is due to the large forces acting between the nucleons of the
nucleus. If we assume that the force of attraction due to strong gravitation
acts between the nucleons in a nucleus, then there must be also powerful forces
of repulsion. These forces arise from the torsion fields of rapidly rotating
nucleons. Typically, the force of the torsion field is weaker than the force of
gravitational attraction of masses. Similarly, magnetic forces are generally
weaker than electrical forces, since in the formula for the magnetic force
there is the squared speed of light, which decreases the value of the force. As
the magnetic forces, the forces of the torsion field considerably grow at the
velocity close to the speed of light, and begin to level off in value with the
electric and gravitational forces, respectively. Thus, in order that the spins
of the nucleons in a nucleus could effectively repel each other, a very fast
rotation of the nucleons is necessary, which generates the field of torsion.
As an illustration, we shall present here a formula
for the total energy of deuterium, the simplest nucleus, consisting of a
neutron and a proton, according to [6]:
,
(18)
where 
is the
gravitational energy of the interaction of neutrons and protons (the coefficient
0.26 reflects a decrease in the interaction force due to the high density of
substance and is calculated in the upgraded model of gravitation of
Fatio-Lesage [5], [10] as the consequence of the exponential attenuation of
flux of gravitons in substance; at low density of substance this coefficient
tends to 1, and the formula for 
takes
Newtonian form),
m3∙kg
–1∙s –2 is the strong gravitational constant according to [5],
– the
elementary electric charge,
– the
vacuum permittivity,
– the electron mass,
– the
distance between the centers of the neutron and the proton,
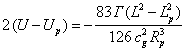– the
change in the energy of the torsion field of strong gravitation of two
nucleons,
which occurs due to the increase in the spin (the
angular momentum) of each nucleon from the value 
to ,
– the
proton radius, approximately equal to the radius of neutron,
– the
propagation speed of gravitation which is close to the speed of light,
– the
energy of interaction between the spins of two nucleons in their gravitational
torsion field,
– the
coefficient, which reflects an increase in the spin of the nucleons as compared
with the value for the angular momentum of the ball in classical physics, and
arises as the consequence of taking into account the relativistic rotation, the
increase in the mass and the momentum,
– the increase in the rotational
energy of the nucleons during their fusion in the nucleus,
– the
moment of inertia of a nucleon.
Our assumption that the rotation of nucleons in their
fusion to the nucleus should be increased, follows from the fact that only in
this case, the repulsive force of the spins will be sufficient to counteract
the attraction of the nucleons under the influence of strong gravitation.
Orientation of nucleon spins in the nucleus of deuterium is of such kind that
produces repulsion of the spins, and during the convergence of nucleons due to
the equal direction of spins there is an increase in rotation of the nucleons
with the increase in the angular momentum because of the effect of
gravitational induction. As a result the nucleons start rotating rapidly and
reach the maximum possible angular momentum.
For the deuteron the total energy is 
MeV,
correspondingly, the binding energy as the absolute value of the total energy
is 
MeV. For more massive nuclei with an increased
number of protons the formula for the total energy instead of (18) can be
written as follows:
, (19)
where 
specifies
the number of nucleons in a nucleus,
the gravitational energy , the energy of interaction between the spins 
and the
change of the rotational energy 
are
calculated for all the nucleons in the nucleus,
– the
electrical energy of protons in the nucleus for the case of their uniform
distribution by the volume
of the nucleus, when 
,
– the
average radius of the nucleus,
– the
charge number of the nucleus or the number of protons.
In literature, as a rule specific binding energy, or
the absolute value of the total energy per nucleon are considered, i.e., the
quantity 
, and its dependence on is built. For
light nuclei the main contribution to (19) is made by the energy of strong
gravitation . Assuming that radius of the nucleus is
approximated by the usual formula 
, where 
m, and the
mass of the nucleus 
, we can write as in [6] a proportional relation:
.
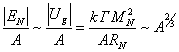This dependence describes well the growth of the
specific binding energy of nuclei up to 
. Then saturation of the energy of strong
gravitational energy takes place, the energy of the nucleus changes not
proportionally to the square of nuclear mass, but much weaker. As it was shown
in [10], the cross section of interaction of gravitons with nucleons is such
that it is enough to put three nucleons in the way of the flux of gravitons in
order to significantly reduce the flux (approximately 2.718 times, this number
is the base of natural logarithms). When the number of nucleons in the nucleus
is more than 17–23 then addition of new nucleons increases less and less the
gravitational energy per nucleon.
At the same time adding protons to the nucleus with
increasing of the mass and the charge of the nucleus leads to a marked increase
in the positive electric energy which begins to compensate the change of the
negative gravitational energy. As a result, at 
for 
the
maximum of the dependence on is
achieved, and then the specific binding energy begins to decrease with the
increase in . Thus, the formulas for the strong gravitation
and for the electromagnetic forces and energies can describe the equilibrium of
nucleons in the nucleus, and also explain the dependence of the specific
binding energy on the mass number. The decrease in the mass of the atomic
nuclei, compared with a sum of the masses of the constituent nucleons, is the
consequence of the opposite fluxes of energy necessary for the emergence of the
binding energy, compared with the case of the ordinary gravitational
contraction of matter.
General
theory of relativity
The axiomatics of general theory of relativity (GTR)
is associated with recognition of the gravitational field as some form of
metric field, and with geometric difference between a curved Riemannian
spacetime and the flat Minkowski spacetime. Currently, GTR is the most famous
and developed theory of gravitation. As the basis of the theory the
Hilbert-Einstein equations for the metric can be considered:
, (20)
where 
− Ricci
tensor,
− the
scalar curvature,
− the
metric tensor,
− the
cosmological constant,
− the
gravitational constant,
− the
speed of light,
− the stress–energy
tensor of substance,
− the
stress–energy tensor of electromagnetic field and other non-gravitational
fields.
If we ignore the cosmological constant and consider
the metric around a spherical, uncharged, non-rotating mass with the density of
its substance and the
tensor 
, where 
is
4-velocity, then in spherical 4-coordinates 
, the
metric tensor as the solution of equation (20) has the following components:
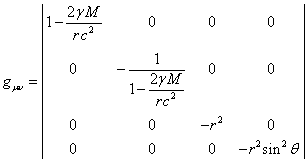. (21)
This is the well-known Schwarzschild solution for the
metric around a massive point body with mass 
, which depends only on the angle 
and the
distance 
between
the attracting center and observation point.
The equation of motion of GTR for the test body around
the attractive mass is as
follows:
,
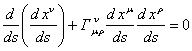(22)
where 
is the
invariant interval,
− the
differential of the proper time of the test body,
− 4-vector
of the test body displacement,
−
Christoffel symbol, which is expressed through the metric tensor and its
derivatives with respect to the coordinates.
If we use the metric tensor (21) to solve equation
(22) for the timelike component , when 
, we obtain the following:
.
(23)
We shall multiply (23) by the value 
, where is mass of
the test body, and look at the situation at infinity. Here 
tends to 1
because of the large value , and the differential of the proper time has the
same form as in special theory of relativity: 
, where 
denotes
the speed of the test body at infinity. Then (23) becomes equality for
infinity:
.
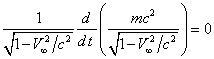In the brackets of the equality we have the
relativistic energy of the body with the mass , which is moving at infinity at the speed . Consequently, (23) can be treated as the law of
conservation of energy of the test body in the gravitational field (in free
fall the energy of gravitational field is converted into the kinetic energy,
and the sum of the negative energy of the field and the positive kinetic energy
is zero). After multiplying (23) by the value and
integrating we obtain the relativistic energy:
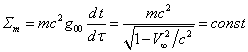. (24)
According to (24), during the fall of the test body to
the attractive center and changing of the radial distance the value 
changes,
as well as the differential of the proper time with respect
to the differential of the coordinate time , but the relativistic energy of the test body
remains unchanged.
We shall assume now that the particles of the
substance of the test body at infinity were once scattered in such a way that
their speed was near zero,
and then the particles will approach a massive body and collide with each
other. If in the collision the particles lose part of their total angular
momentum, and convert part of their energy into the thermal energy of the
collision 
, which is emitted from the system, then a
stationary rotation of substance around the center of attraction is possible.
The condition for this is the satisfying of the virial theorem, according to
which the absolute value of the total energy of the system must be equal to the
energy emitted from systems: 
. As a result the relativistic energy of the test
body, falling from infinity at zero initial velocity to the source of
gravitational field, will decrease by the amount :
. (25)
Thus, in general theory of relativity the substance of
the mass , rotating in a stationary state around the
center of attraction, must reduce its relativistic energy due to the
contribution of the negative total energy 
.The same conclusion will be valid, if the
attractive center arises due to the collapse of a massive cloud of substance,
which reduces in the course of time its angular momentum by means of
electromagnetic radiation. Equation (25) by its meaning does not coincide with
(3), in which the total energy is not added
but subtracted from the rest energy.
Covariant
theory of gravitation
In contrast to the general theory of relativity, the
covariant theory of gravitation (CTG) is based on the axioms of
Lorentz-invariant theory of gravitation [6], [11], and is a covariant
generalization to the curved Riemannian spacetime. Gravitation in CTG is
considered not fictitious geometric, but an actual physical force, and can be
substantiated using Fatio-Le Sage's theory of gravitation. In CTG the substance
through a 4-vector of density of momentum 
generates
a gravitational field with a 4-potential 
,
satisfying the wave equation in the Riemannian spacetime:
, (26)
where – the
propagation speed of gravitation which is close to the speed of light,
is
4-d'Alembert operator,
is the
Ricci tensor with mixed indices,
− the gravitational
constant.
4-vector of density of momentum is
determined by the product of the density of substance , found in the frame of reference of the
substance unit at rest, and the 4-velocity: 
. If we use the approximation of weak field and
small velocities, when the CTG is transformed into Lorentz-invariant theory of
gravitation, the 4-velocity is as follows:
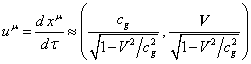. (27)
The same expression of the 4-velocity (27) with
condition 
is adopted
in general relativity for the case of the weak field and small velocities. In
Riemannian space we can introduce [6] the operator of differentiation with
respect to the proper time 
:
,
(28)
where the symbol 
denotes the total differential in
curved spacetime,
is the covariant derivative.
When the operation of the covariant antisymmetric
tensor product of the covariant gradient operator and the covariant 4-vector
potential 
is used the gravitational field strength
tensor has the form:
,
In view of 
the
relationship between the substance and the field (26) is as follows:
.
(29)
The covariant 4-vector of potential is defined as:
,
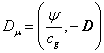where 
– the scalar
potential,
– the vector
potential.
The intrinsic properties of gravitational field strengths, independent
on the material sources, are set by the relation:
. (30)
Relations (29) and (30) have the form in which
equations of gravitational field of CTG are covariant in any frame of reference.
The field in its turn affects the substance, creating
a gravitational force. 4-vector of density of the gravitational force is
defined by:
,
(31)
where 
is the
stress–energy tensor constructed with the help of the tensor of strengths of
the gravitational field and
equations (29) – (31). The presence of the tensor 
distinguishes CTG from the general relativity,
in which an exact expression for the stress–energy tensor of gravitational
field is absent.
The general definition of force in CTG is found by
means of (28):
. (32)
The electromagnetic force is defined by:
,
where 
– the
electromagnetic tensor,
–
4-current,
– the
charge density in the reference frame where the charge is at rest,
– the
electromagnetic stress–energy tensor.
If there are only two fundamental fields,
gravitational and electromagnetic, which create forces, then the equation of
motion of the substance unit takes the form:
. (33)
As it was shown in [11], the equation of motion in
general relativity is derived from (33) as a special case.
To determine the spacetime metric the Hilbert-Einstein
equations [12] are used:
. (34)
In contrast to (20), in CTG the gravitational field,
along with the electromagnetic field is involved in obtaining the metric, so the
right side of (34) contains the stress–energy tensor 
of
gravitational field. The stress–energy tensor of substance in CTG is
constructed so that the covariant derivative of this tensor, taken with
contravariant indices, would give the force density (32): 
. If we take the covariant derivative of (34),
the left side vanishes because of the properties of the metric tensor. This
again gives the equality for the density of forces (33):
.
The solution of the equation for the metric (34)
around an uncharged ball at rest gives the components of the metric tensor in
spherical 4-coordinates , [6] :
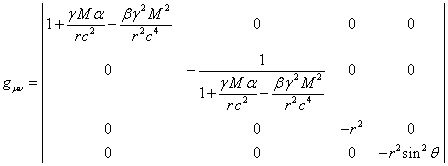. (35)
The coefficients 
and 
in (35)
from equations (34) are not defined and should be specified for each particular
system of bodies.
Using the metric tensor (35), we can find the solution
to the equations of motion (33) for the timelike component 
, when 
. In the case of the weak gravitational field and
at constant density 
of the
substance unit we obtain:
,
or 
.
(36)
At infinity tends to
1, , where denotes
the velocity of the test body at infinity, and 
. We shall suppose 
, then, after multiplication by 
(36) can
be written as follows:
. (37)
According to (37) the substance, which had at infinity
the relativistic energy , during a fall in the gravitational field
increases its energy by the value equal to the absolute value of the potential
energy of the field 
. Although in CTG there is difference of
expressions and from the
corresponding expressions in general relativity, in (37) an approximate
equality between the absolute value of change of the potential energy of
gravitational field and the change in the kinetic energy of substance motion is
satisfied.
If for this system the virial theorem is valid, for
which the decrease in the angular momentum of the falling substance, emission
of energy from the
system and increase in the kinetic energy of the substance by the value 
are
required, then the relativistic energy is equal to:
, (38)
where 
is the
total energy of mass in
gravitational field.
If the gravitation is created by a stationary system
with a mass , then the energy in (38)
will characterize the change in the relativistic energy of the system that has
occurred due to the action of gravitational field, the interaction of particles
of substance and emission from the system. Relation (38) has the same form as
(3), where before the total energy there is a
negative sign. We can see that difference between the results of CTG and
general relativity is due to difference in the equations of motion (33) and
(22).
Conclusions
Having examined some cases of mass-energy relation, we
made the assumption that if the system loses energy in the form of emission or the
work is done on the surrounding bodies, then the total energy of the particles
of the system must be subtracted from the rest energy of the particles
constituting the system. For fundamental forces the total
energy is negative, which leads to an increase in the mass of the particles
system as compared with the sum of the masses of the particles separately. In
particular, the mass of a star in accordance with the covariant theory of
gravitation can be larger than the total mass of fragments of stellar substance.
This is confirmed in [13]. In another case, when for the formation of the
system it is necessary to add energy to it or to do work on it, the total
energy of the particles in the system should be added to the rest energy of the
particles constituting the system. In some cases this leads to the decrease in
the relativistic energy and the mass of the system (an example is the formation
of nuclei of the nucleons).
Our assumptions are essentially the opposite to the
standard view, for which a suitable form of the total energy is always just
added to the rest energy of the particles constituting the system. In the
general theory of relativity as for the stars and so for the atomic nuclei,
this leads to a decrease in their mass as compared with the rest mass of the
particles constituting these objects, and heating of the body increases its
mass. Apparently, in such situation additional confirmation is required,
whether in fact there is increase, or decrease in the inert and gravitational
masses of massive complex objects as compared with the sum of the masses of
their parts.
In this connection, we should consider the following.
If we calculate the share of the gravitational binding energy in relation to
the rest energy of the substance for a typical neutron star, this share could
reach 6 %. The same value is expected for increase (or decrease) in the
gravitational mass of the star, and hence in the force acting on the test body
near the star. On the other hand, the force acting on the body, according to the
Fatio-Le Sage's theory of gravitation, depends also on the density of the body. For two bodies of low density
the law of Newton's gravitational force is satisfied with sufficient accuracy,
but when the substance density of the interacting bodies reaches the density of
neutron stars, the force decreases in magnitude and is equal to 26 % of the
Newtonian force [6]. As it can be seen, the effect of changing of the
gravitational mass can depend not only on the total energy of bodies, but also
on other parameters, which can make the experimental verification of the theory
more complicated.
References
1.
Болотовский Б. М. Оливер Хевисайд. — М.: Наука,
1985. — 254 с.
2.
Poincaré H. La théorie de
Lorentz et le principe de réaction
// Archives
néerlandaises des sciences exactes et naturelles. — 1900. — Vol. 5. — P. 252—278.
3. Einstein, A. (1905), "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?", Annalen der Physik 18: 639–643, Bibcode 1905AnP...323..639E, doi:10.1002/andp.19053231314. See also the English translation.
4. Fedosin S.G. Energy, Momentum, Mass and Velocity
of Moving Body. vixra.org, 13 Jun 2011.
5.
Fedosin S.G. Fizika i filosofiia podobiia: ot
preonov do metagalaktik. – Perm,
1999. – 544 p. Tabl. 66, Pic. 93, Ref. 377. ISBN 5-8131-0012-1.
6. Fedosin S.G. Fizicheskie teorii i beskonechnaia
vlozhennost’ materii. – Perm, 2009. – 844 p. ISBN 978-5-9901951-1-0.
7.
2011 CODATA recommended value .
8. WolframAlpha, computational knowledge engine.
9. Comments to
the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia
vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289.
ISBN 978-5-9901951-1-0 (in Russian).
10.
Fedosin S.G. Model of Gravitational Interaction in the Concept of
Gravitons. Journal of Vectorial Relativity, Vol. 4, No.
1, March 2009, P.1–24.
11.
Fedosin S.G. The General Theory of Relativity,
Metric Theory of Relativity and Covariant Theory of Gravitation: Axiomatization
and Critical Analysis. vixra.org, 26 Mar 2011.
12.
Fedosin
S.G. The Principle
of Least Action in Covariant Theory of Gravitation.
Hadronic Journal, February 2012, Vol. 35, No. 1, P. 35 – 70.
13.
Fedosin
S.G. The
Hamiltonian in covariant theory of gravitation.
vixra.org, 22 May 2012.
Source:
http://sergf.ru/nven.htm