Caspian
Journal of Applied Sciences Research, 2012, Vol. 1, No 13, P. 1 – 15.
УДК 53.02+
530.12:531.51 +530.131:531.62+531.35+531.422+536.1+536.75
Принцип пропорциональности массы и энергии: новая версия
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
e-mail intelli@list.ru
Рассматривается сущность массы и её взаимосвязь с релятивистской
энергией. Предполагается, что энергия покоя равна полной энергии связи тела и
может быть найдена через энергии фундаментальных полей, связанных с веществом
данного тела. Масса как мера инерции тела вычисляется через релятивистскую
энергию и релятивистский импульс. Делается вывод о том, что при излучении энергии
из системы масса системы должна не уменьшаться, а увеличиваться.
Противоположным случаем является нагревание тел от внешних источников, что
должно сопровождаться увеличением энтропии и уменьшением массы данных тел. На
основе сильной гравитации даётся объяснение дефекту масс атомных ядер. Выводы
общей теории относительности и ковариантной теории гравитации в отношении массы
и энергии гравитационного поля оказываются противоположными – в общей теории
относительности релятивистская энергия и масса тела уменьшаются за счёт
массы-энергии собственного гравитационного поля, а в ковариантной теории
гравитации масса-энергия гравитационного поля увеличивает релятивистскую
энергию и массу тела.
Ключевые слова: масса; энергия; принцип эквивалентности; тензор энтропии; дефект массы.
The Principle of Proportionality of
Mass and Energy: New Version
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
The
essence of mass and its relation to the relativistic energy is considered. It
is assumed that the rest energy is equal to the binding energy of the body and
can be found through the energies of fundamental fields associated with the
substance of the body. Mass as a measure of inertia is calculated by
relativistic energy and relativistic momentum. The conclusion is made that
after radiation of energy from a system the mass of the system must not
decrease, but increase. The opposite case is heating of bodies by external
sources, which must be accompanied by an increase in entropy and decrease in
the mass of the bodies. On the basis of strong gravitation mass defect of
atomic nuclei is explained. Conclusions of the general theory of relativity and
the covariant theory of gravitation with respect to the mass and energy of
gravitational field are opposite – in the general theory of relativity,
relativistic energy and mass of a body are reduced by the mass-energy of its
own gravitational field, and in the covariant theory of gravitation the
mass-energy of the gravitational field increases the relativistic energy and
body mass.
Keywords: mass; energy; principle of
equivalence; tensor of entropy; mass defect.
Познание сущности массы и энергии, а также способов их
определения, являются одной из важных задач физики. Это связано с широким употреблением
закона сохранения энергии-импульса в самых различных областях и с возможностью
вычисления действующих сил через градиенты энергии в пространстве-времени.
Связь между массой и энергией должна
быть наиболее простая в системе отсчёта, в которой тело покоится и не
вращается, так как при этом импульс и момент импульса тела равны нулю и
кинетическая энергия линейного движения тела как целого и энергия вращения в
расчёте массы не участвуют.
Изучение взаимосвязи массы и энергии покоящегося тела в период
становления теории относительности привело к соотношению:
,
(1)
где 
– релятивистская
энергия в покое,
– масса тела,
– скорость света.
Вначале считалось, что коэффициент 
в (1) достаточно
близок к единице, затем благодаря усилиям О. Хевисайда (1889) [1], А. Пуанкаре
(1900) [2], А. Эйнштейна (1905) [3] и ряда других физиков было установлено, что
.
Из соотношения (1) не следует, что масса и релятивистская
энергия покоя являются синонимами, обозначением одного и того же. С одной
стороны, масса тела есть интегральное свойство, определяющее инертность тела
при получении ускорения под действием силы. Интегральность здесь означает, что
вклад в массу делает не только вещество тела, но и физические поля, связанные с
этим веществом, а также и поля от внешних источников в объёме тела. С другой
стороны, энергия ассоциируется более с законом сохранения энергии, с
возможностью передачи энергии из одного места в другое различными способами и в
различных формах, такими как теплоперенос, электромагнитное излучение,
электрический ток и т.д. Сила 
, действующая на тело, определяется как скорость изменения
импульса, причём масса тела непосредственно входит в импульс 
в качестве
сомножителя. При расчёте силы во внешнем поле часто используют формулу, по
которой сила оказывается градиентом потенциальной энергии тела 
, взятым с обратным знаком. Отсюда следует следующее:
. (2)
Из (2) видно, что хотя в массу (а значит и в импульс) делают
вклад все виды энергии тела, но сила как скорость изменения импульса может
зависеть от градиентов лишь некоторых видов энергий. Если взять среднее по
всему объёму, то энергии без градиентов и потоков энергии не вызывают силы и
ускорения, хотя и участвуют в образовании массы тела. В связи с этим удобно
полагать, что масса отражает статические интегральные гравитационные и
инерционные свойства тела, появляющиеся как результат потоков энергий,
взаимодействующих с телом.
Как было описано в [3], масса тела, излучающего некоторую
энергию 
в виде двух противоположно
направленных фотонов, должна уменьшаться на величину, равную 
. Для проверки данного вывода мы вновь повторим мысленный
эксперимент с телом, излучающим фотоны. При этом мы будем использовать формулы
для релятивистской энергии и импульса из [4]:
, 
, 
,
(3)
где есть положительная по
величине релятивистская энергия тела в покое,
– полная энергия
частиц тела на атомном уровне, включающая в себя различные виды энергии,
связанные с атомами и молекулами вблизи абсолютного нуля температуры: сильное
взаимодействие, скрепляющее вещество элементарных частиц и удерживающее нуклоны
в атомных ядрах; электромагнитное взаимодействие частиц; энергия движения
вещества внутри нуклонов и энергия движения нуклонов в ядрах и электронов в
атомах; энергия вращения атомов и молекул; энергия колебаний атомов в
молекулах, и т.д.,
– полная энергия
покоящегося тела на макроуровне, с учётом внутренней кинетической энергии 
в виде хаотической
кинетической энергии движения атомов и молекул и энергии турбулентного движения
потоков вещества, а также энергии фундаментальных макроскопических полей.
Сумма 
задаёт внутреннюю
энергию системы, обычно используемую в термодинамике в приближении слабого поля
взаимодействия частиц системы. Согласно (3), релятивистская энергия есть
энергия связи тела, или полная энергия, взятая с отрицательным знаком.
По определению полную макроскопическую энергию можно разбить на три
компоненты:
,
(4)
где 
и 
есть полные энергии
макроскопических гравитационных и электромагнитных полей вещества тела
соответственно, вычисляемые как внутри тела, так и за его пределами. В эти же
энергии следует включать и энергии полей от внешних источников, попадающие
внутрь объёма тела и изменяющие энергию вещества.
Учтём в (4) теорему вириала, согласно которой модуль
потенциальной энергии поля в среднем в два раза больше внутренней кинетической
энергии для тел, находящихся лишь под действием собственных гравитационных и
электромагнитных полей:
,
. (5)
Для энергии аналогично (5) можно
записать:
,
(6)
где 
есть полная энергия
поля сильной гравитации, которая предполагается на уровне элементарных частиц и
атомов и в качестве сильного взаимодействия скрепляет вещество нуклонов,
нуклоны в атомных ядрах, а также является одной из составляющих, удерживающих
электроны на их орбитах в атомах,
– электромагнитная
энергия в веществе элементарных частиц и вокруг них в атомах.
С учётом (5) и (6) релятивистская энергия (3) тела в покое
может быть записана так:
. (7)
Основной вклад в энергию вносит отрицательная
энергия поля сильной
гравитации, что обеспечивает положительность релятивистской энергии и массы
тела, определяемой выражением:
.
(8)
Перейдём теперь к анализу мысленного эксперимента. Пусть есть
покоящееся тело и из него излучаются в противоположные стороны два фотона, один
с энергией 
вдоль оси 
, и другой с такой же энергией против оси . Будем считать, что излучение фотонов происходит только за
счёт изменения макроскопических полей, тогда баланс энергий до и после
излучения имеет вид:
.
(9)
После излучения тело остаётся покоящимся, так как импульсы
фотонов противоположны и суммарный импульс системы остаётся равным нулю. В (9)
предполагается, что в момент излучения меняются компоненты энергии , причём энергия фотонов взята со знаком минус, что означает
убыль энергии тела за счёт излучения. Отсюда следует, что 
, и следовательно 
. Обе энергии и 
отрицательны, так что
для модулей энергии получается: 
. Из (9) видно также, что релятивистская энергия 
становится больше, чем
энергия . Это влечёт за собой и увеличение массы тела после излучения
из него фотонов: 
. Данный результат согласуется с тем, что чем больше энергии
излучает какая-нибудь звезда, тем больше она сжимается и разогревается. Полная
энергия такой звезды
становится всё более отрицательной, а положительная внутренняя кинетическая
энергия в (5) растёт, что
согласно (7) и (8) увеличивает массу звезды. Одним из оснований для выбора
отрицательного знака перед в (7) является
симметрия данного выражения, когда перед также стоит знак
минус. Кроме этого, энергия гравитации при сжатии звезды превращается во
внутреннюю кинетическую энергию движения вещества и в энергию излучения, причём
по теореме вириала последние энергии приблизительно равны друг другу. Если
энергия гравитации порождает энергию излучения, то в той же степени энергия
гравитации может порождать и дополнительную релятивистскую энергию и массу
звезды. При этом в системе звезда + вселенная выполняется закон сохранения
энергии – отрицательное изменение гравитационной энергии звезды при её сжатии
компенсируется положительным изменением внутренней энергии вещества и
появлением энергии излучения от звезды.
В принципе, никакое электромагнитное излучение и излучение
фотонов невозможно, если над электрическими зарядами не производится работа.
Если заряд ускоряется гравитационной силой, то именно работа гравитации будет
увеличивать энергию системы с передачей части этой энергии излучению от заряда.
В бетатроне работа магнитного поля преобразуется в ускорение электронов,
создающих синхротронное излучение. В атоме сильная гравитация и электрическое
поле ядра выполняют работу над электроном при его переходе из одного
энергетического состояния в другое, что приводит к излучению из атома. Во всех
случаях выполненная работа превышает энергию излучения, что даёт возможность
увеличивать релятивистскую энергию излучающей системы в момент излучения.
Описанное выше обоснование соотношения (9) и выбора
отрицательного знака перед энергией фотонов 
отсутствует в работе
[3]. Вместо этого рассматривается механическая модель явления, когда фотоны как
некоторые части тела покидают это тело и уносят часть его массы.
Соответственно, в такой картине знак перед энергией фотонов выбирается
положительный, а масса тела после излучения фотонов должна уменьшаться. Однако
фотоны не являются частью тела, поскольку они порождаются за счёт абсолютного
ускорения зарядов тела без уменьшения величины этих зарядов (если масса тела
может меняться за счёт изменения энергии тела, то заряд тела остаётся до тех пор,
пока не будет удалён с тела либо не будет скомпенсирован зарядом
противоположного знака). Поэтому убыль релятивистской энергии тела за счёт
передачи энергии фотонам должна быть возмещена увеличением, а не уменьшением
энергии и массы тела.
Рассмотрим теперь излучение фотонов из тела, движущегося со
скоростью 
вдоль оси 
. Фотон, излучённый в направлении оси 
, будет иметь голубое смещение своей длины волны и
увеличенную энергию, а у фотона, излучённого в противоположном направлении,
будет красное смещение длины волны и уменьшенная энергия. Суммарная энергия
фотонов с учётом формулы для эффекта Доплера будет равна 
, а суммарный импульс фотонов равен 
и направлен вдоль
скорости движения тела.
Если учесть формулы (3) , то баланс энергий и импульсов до и
после излучения фотонов даёт:
,
. (10)
В (10) перед энергией и импульсом фотонов стоит знак минус,
поскольку фотоны уносят из тела часть его энергии и импульса. При этом в момент
излучения фотонов происходит соответствующее увеличение массы тела, его
релятивистской энергии и импульса. После сокращения одинаковых членов
соотношения (10) переходят в (9). Это означает, что различие формул для
процессов излучения фотонов неподвижного и движущегося тела связано лишь с
преобразованием Лоренца и определяется фактором 
.
Нагревание
тел
На основе вышеизложенного можно прийти к тому, что при нагревании
тела внешними источниками энергии масса тела должна уменьшаться. Как было
найдено в [5] на основе лоренц-инвариантной термодинамики, количество теплоты 
, возникающее в некотором объёме тела 
за время 
, определяется интегралом:
,
(11)
где 
– плотность потока
гравитационной энергии,
– плотность потока
электромагнитной энергии (вектор Умова-Пойнтинга),
– единичный вектор
нормали к поверхности с площадью 
, окружающей объём .
Согласно (11), увеличение теплоты может быть описано через
входящие потоки энергии фундаментальных полей – либо через интеграл от
дивергенций потоков энергии по объёму, либо с помощью теоремы Гаусса через
интеграл от потоков энергии по площади. Соотношение (11) проще понять, если
учесть следующие формулы:
, 
,
(12)
где 
и 
есть плотности энергии
гравитационного и электромагнитного полей в виде временных компонент
соответствующих тензоров плотности энергии-импульса,
и 
– плотности массового
и электрического тока соответственно,
и 
– напряжённости гравитационного
и электромагнитного полей (гравитационное ускорение и электрическая
напряжённость).
Если подставить (12) в (11), то видно, что количество теплоты
в объёме тела увеличивается тогда, когда растёт энергия поля, а также когда за
счёт энергии полей в единице объёма за единицу времени выполняется работа 
. Дифференциал энтропии выражается формулой:
,
(13)
где 
есть абсолютная
температура Кельвина.
Согласно (13), при нагревании тела от внешних источников
энтропия тела растёт. Если же энергия излучается из тела в процессе
гравитационного сжатия и нагрева вещества, то полная энергия тела уменьшается
на величину и приращение энтропии 
отрицательно. Это
связано с тем, что хотя вещество при сжатии и уменьшении объёма нагревается и
энтропия вещества растёт, но ещё более изменяется отрицательная энтропия
гравитационного поля тела, так что суммарная энтропия вещества и поля
отрицательна. Для энтропии шарообразного тела мы вывели формулу [5]:
, (14)
где радиус-вектор 
отсчитывается от
центра тела,
– давление в
сопутствующей системе отсчёта,
есть функция сжатия, калиброванная таким образом, чтобы
плотность энергии покоя вещества равнялась величине 
,
– плотность
покоящегося вещества.
В (14) интегрирование идёт по всему объёму 
пространства как
внутри, так и снаружи тела. Вклад в отрицательную энтропию тела вносит в
основном градиент от плотности энергии гравитационного поля 
, и градиент давления . Оценка энтропии, приходящейся на одну частицу идеального
газа в гравитационно-связанном шаре с постоянной по объёму температурой, даёт
значение 
, где 
есть постоянная
Больцмана.
По мере излучения энергии из тела энтропия тела становится
всё более отрицательной, энтропия уходящего излучения положительна, в
результате полная энтропия тела и излучения равна нулю. Этот вывод следует из
теоремы вириала и из (13), в которой означает как теплоту
нагрева тела при его гравитационном сжатии, так и энергию, уносимую уходящим
излучением. Нулевая энтропия была и в самом начале процесса образования тела,
когда вещество было неподвижно и находилось на бесконечности в распылённом
состоянии.
В работе [6] мы получили лоренц-инвариантное выражение
первого закона термодинамики, нашли тензорную функцию химического потенциала, тензорную функцию работы-энергии
системы, а также тензорную функцию теплоты 
:
,
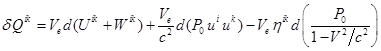(15)
где 
есть инвариантный
объём малого элемента вещества либо малый объём пространства, занимаемого полем
в отсутствие вещества,
и 
– тензоры плотности
энергии гравитационного и электромагнитного полей,
– 4-скорость вещества,
– тензор
пространства-времени Минковского.
Из (15) следует, что при неизменном объёме элемента
вещества приращение теплоты происходит от приращений плотности энергии-импульса
полей и изменения внутреннего давления 
, завися для внешнего наблюдателя от 4-скорости движения. Все
члены, приведённые в (15), способны напрямую увеличивать кинетическую
температуру элемента вещества и поэтому входят в состав 
. Для получения количества теплоты тела как совокупности
элементов вещества следует просуммировать по всем элементам
объёма. Приращение тензора энтропии определяется аналогично (13):
.
Симметричный тензор энтропии есть следующий интеграл по
объёму:
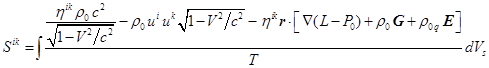, (16)
где 
есть плотность заряда.
Для элемента вещества гравитационно-связанного тела после
ряда упрощений получается формула для временной компоненты тензора энтропии:
,
где 
есть изменение
плотности вещества на длине элемента вещества,
– газовая постоянная, 
– количество вещества в молях.
Можно показать, что не только 
, но и другие компоненты тензора 
отрицательны. Из (16) следует, что энтропия
элемента вещества пропорциональна отношению модуля упорядоченной энергии в этом
элементе к энергии хаотического теплового движения частиц вещества, взятому со
знаком минус. Под упорядоченной энергией подразумевается энергия направленного
движения элемента вещества, энергия сжатия от давления и потенциальная энергия
элемента вещества в гравитационных и электромагнитных полях. Энтропия
оказывается функцией состояния системы потому, что если состояние системы
задано с помощью ряда физических величин, то в каждом таком состоянии
осуществляется, после истечения некоторого времени релаксации, как правило
только одно определённое соотношение между упорядоченной и неупорядоченной
энергиями системы, не зависящее от пути перехода в данное состояние. Это
соотношение и фиксируется с помощью понятия энтропии.
В теории бесконечной вложенности материи [6] считается, что источником
упорядочения и упорядоченной энергии тел являются потоки гравитонов, свойства
которых близки к свойствам фотонов и нейтрино, а также высокоэнергичных
заряженных частиц. Именно такие кванты поля и частицы, возникающие на низших
уровнях материи, благодаря своей относительно большой энергии по сравнению со
своей массой обладают наибольшей упорядоченностью в нашем мире и переносят её в
пространстве.
Поток упорядочения, поступающий в некоторую гравитационную систему с потоком
гравитонов, генерирует в системе негэнтропию, поскольку уходящий из системы
поток гравитонов имеет более низкую температуру, при почти той же самой
энергии, что и энергия входящего потока гравитонов. Данная негэнтропия
позволяет уменьшать энтропию системы в сторону отрицательных значений. Кроме
этого, уходящее из системы излучение, обычно электромагнитное, имеет свою
собственную энтропию, так что приблизительно около половины негэнтропии от потоков гравитонов
тратится на потерю системой энтропии за
счёт уходящего излучения.
В соответствии с вышеизложенным и с [4] мы полагаем, что наблюдаемое
нагревание некоторого объекта благодаря гравитационному сжатию приводит к
увеличению массы этого объекта. Этот процесс сопровождается излучением фотонов
из объекта с общей энергией, равной релятивистской энергии объекта без учёта
энергии покоя, и равной модулю полной макроскопической энергии
(макроскопической энергии связи). При этом как полная энергия, так и энтропия
объекта отрицательны. В обратном процессе излучение извне нагревает объект,
увеличивает полную макроскопическую энергию и энтропию, а значит уменьшает
релятивистскую энергию покоя и связанную с ней массу объекта.
Ядерная
энергия
В современной физике считается, что для определения
релятивисткой энергии тела необходимо к энергии покоя составляющих его частиц
добавить полную энергию тела с учётом механической энергии частиц и энергии
полей. Для фундаментальных сил полная энергия как правило отрицательна, так что
релятивистская энергия и масса тела получаются меньше, чем энергия и сумма масс
всех частиц тела, разделённых друг от друга. В теории бесконечной вложенности материи существует
бесконечно много уровней материи с находящимися на них объектами
соответствующих масс. Если на некотором основном уровне материи взять
достаточно много объектов и начать складывать из них более массивные объекты,
то за счёт отрицательной полной энергии относительная масса объектов будет всё
меньше и меньше на каждом последующем уровне материи, по отношению к сумме масс
исходных объектов.
Согласно нашим предположениям, полная энергия в гравитационном поле
входит в релятивистскую энергию с отрицательным знаком, что приводит не к
уменьшению, а к увеличению масс объектов по мере роста массы этих объектов.
Если рассматривать вопрос с философской точки зрения, то выводы о вероятном
уменьшении или увеличении относительной массы объектов по мере перехода к
высшим уровням материи кажутся одинаково допустимыми. По всей видимости, выбор
может быть сделан путём сравнения с экспериментальными данными.
Наиболее ярко связь между массой и энергией проявляется в
случае синтеза лёгких ядер и при распаде массивных ядер, когда небольшие
разницы в массах исходных и конечных продуктов реакций сопровождаются
выделением большого количества энергии. В Таблице 1 согласно [7], [8] приведены
массы некоторых ядер в сравнении с суммой масс отдельных протонов и нейтронов,
из которых можно было бы составить данные ядра.
Таблица 1
|
Ядро |
Число
нейтронов, |
Число
протонов, |
|
|
|
|
|
|
1 |
1 |
1,674 927 351 |
1,672 621 777 |
3,343 583 48 |
0,003 965 65 |
|
|
34 |
28 |
56,947
529 93 |
46,833
409 75 |
102,808
9 |
0,972
04 |
|
|
146 |
92 |
244,539
393 |
153,881
203 |
395,208
8 |
3,211
8 |
Согласно Таблице 1, масса какого-либо ядра меньше, чем
суммарная масса нуклонов, из которых образуется это ядро. Дефект массы,
приведённый в последнем столбце Таблицы 1, таков, что уменьшение массы ядра
может достигать почти 1 %. В стандартной модели считается, что при объединении
нуклонов их суммарная масса уменьшается за счёт отрицательной полной энергии
ядра. Если же исходить из наших предположений, то аналогично (3) для
релятивистской энергии и массы покоящегося ядра следует записать:
, 
, (17)
где 
– суммарная полная
энергия свободных нейтронов, необходимых для образования ядра,
– суммарная полная
энергия свободных протонов, входящих в состав ядра,
– полная энергия ядра
при соединении нуклонов, состоящая из кинетической энергии движения и вращения
нуклонов в ядре, и из потенциальной энергии их взаимодействия посредством
гравитационных и электромагнитных полей согласно гравитационной модели сильного
взаимодействия.
Заметим, что в (17) перед полной энергией мы поставили знак
плюс, в отличие от знака минус, стоящего перед полной энергией 
в (3). Это связано с
тем, что при гравитационном сжатии энергия гравитационного поля переходит как в
излучение в окружающую среду, так и в нагрев вещества, создавая тем самым массу
излучения и дополнительную массу тела, как это видно из (3). Но ситуация с
образованием атомного ядра из нуклонов оказывается иной. Для возникновения ядра
необходимо либо нагреть нуклоны от внешнего источника до температуры,
достаточной для начала реакции слияния ядер, либо совершить над нуклонами определённую
работу. Если при гравитационном сжатии из системы излучаются фотоны, то в
противоположность этому для слияния ядер необходимо каким-либо путём ввести в
систему дополнительную энергию. Это напоминает эффект от теплового нагревания,
рассмотренный в предыдущем разделе и приводящий по нашему мнению к уменьшению
массы системы.
С формальной точки зрения, соотношение (3) описывает процесс
создания массы фотонов в окружающем пространстве и создания дополнительной
массы системы в виде 
. Для описания образования ядра и изменения его массы можно
предположить, что взаимодействие между нуклонами приводит к некоторой
отрицательной массе фотонов (фотоны не рождаются, а наоборот поглощаются
системой, либо над системой производится работа) и к некоторой полной энергии,
взятой со знаком минус. Подстановка в (3) вместо 
полной энергии , но взятой со знаком минус, даёт изменение массы 
и знак плюс перед 
в (17). Поскольку
полная энергия сама по себе
отрицательна, то в (17) масса ядра 
будет меньше суммарной
массы протонов и нейтронов, составляющих ядро.
Каким же образом нуклоны удерживаются в атомных ядрах? В [6]
мы привели модели некоторых простых ядер и описали силы, благодаря которым
нуклоны могут находиться в ядре в равновесии. Аналогично с целью обоснования
устойчивости некоторых адронов мы в [9] построили их модели на основе связи
нуклонов и лёгких мезонов. Прочность ядер обусловлена большими силами,
действующими между нуклонами ядра. Если считать, что между нуклонами в ядре
действует притяжение сильной гравитации, то ему должны противодействовать мощные
силы отталкивания. Эти силы возникают от полей кручения быстро вращающихся
нуклонов. Как правило, сила от поля кручения слабее, чем сила от
гравитационного притяжения масс. Точно также магнитные силы обычно слабее
электрических сил, поскольку в формуле для магнитной силы стоит квадрат
скорости света, уменьшающий значение силы. Как магнитные силы, так и силы от
поля кручения заметно растут при скоростях, близких к скорости света, и
начинают выравниваться по величине с электрическими и гравитационными силами
соответственно. Таким образом, для того, чтобы спины нуклонов в атомном ядре
могли эффективно отталкиваться друг от друга, необходимо очень быстрое вращение
нуклонов, генерирующее поля кручения.
В качестве иллюстрации приведём здесь формулу для полной
энергии дейтерия, простейшего ядра, состоящего из нейтрона и протона, согласно
[6]:
,
(18)
где 
– гравитационная энергия при взаимодействии нейтрона и
протона (коэффициент 0,26 отражает уменьшение силы взаимодействия из-за высокой
плотности вещества и вычисляется в модернизированной модели гравитации
Фатио-Лесажа [5], [10] как следствие экспоненциального затухания потока
гравитонов в веществе; при малой плотности вещества данный коэффициент
стремится к единице, а формула для 
приобретает
ньютоновский вид),
м3∙кг
–1∙с –2 есть постоянная
сильной гравитации согласно [5],
– элементарный
электрический заряд,
– электрическая
постоянная,
– масса электрона,
– расстояние между
центрами нейтрона и протона,
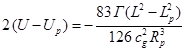– изменение энергии
поля кручения сильной гравитации обоих нуклонов, происходящее за счёт
увеличения спина (момента импульса) каждого из нуклонов от значения 
до 
,
– радиус протона,
приблизительно равный радиусу нейтрона,
– скорость
распространения гравитации, близкая по значению к скорости света,
– энергия
взаимодействия спинов двух нуклонов в создаваемом ими гравитационном поле
кручения,
– коэффициент, отражающий увеличение спинов нуклонов по
сравнению со значением для момента импульса шара в классической физике, и
возникающее как следствие учёта релятивистского вращения, увеличения массы и
момента импульса,
– увеличение энергии
вращения нуклонов при их соединении в ядро,
– момент инерции
нуклона.
Наше предположение о том, что вращение нуклонов при их
соединении в ядро должно увеличиваться, следует из того, что только в этом
случае сила отталкивания спинов будет достаточной для противодействия
притяжению нуклонов под действием сильной гравитации. Ориентация спинов
нуклонов в ядре дейтерия такова, что при этом возникает сила отталкивания
спинов, причём по мере сближения нуклонов вследствие одинакового направления
спинов происходит раскрутка нуклонов с увеличением момента импульса за счёт
эффекта гравитационной индукции. В результате нуклоны быстро раскручиваются и
достигают предельно возможного момента импульса.
Для дейтрона полная энергия 
МэВ, соответственно, энергия связи как модуль полной энергии
равна 
МэВ. Для более массивных ядер с увеличенным количеством
протонов формула для полной энергии вместо (18) может быть записана так:
, (19)
где 
задаёт число нуклонов
в ядре,
гравитационная энергия , энергия взаимодействия спинов 
и изменение энергии
вращения 
вычисляются для всех
нуклонов ядра,
– электрическая
энергия протонов ядра для случая их однородного распределения по объёму ядра,
когда 
,
– средний радиус ядра,
– зарядовое число ядра
или число протонов.
В литературе как правило рассматривается величина энергии
связи или модуля полной энергии в расчёте на один нуклон, то есть величина 
, и строится её зависимость от . Для лёгких ядер основной вклад в (19) вносит энергия
сильной гравитации . Полагая, что радиус ядра аппроксимируется обычной формулой 
, где 
м, а масса ядра 
, мы как в [6] можем записать
пропорциональную зависимость:
.
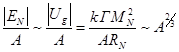Данная зависимость хорошо описывает рост удельной энергии
связи ядер вплоть до 
. Далее происходит насыщение энергии сильной гравитации, энергия ядра изменяется
уже не пропорционально квадрату массы ядра, а гораздо слабее. Как было показано
в [10], сечение взаимодействия гравитонов с нуклонами таково, что достаточно
поставить на пути потока гравитонов три нуклона для того, чтобы существенно
уменьшить этот поток (приблизительно в 2,718 раз, это число есть основание
натурального логарифма). При количестве нуклонов в ядре более 17–23 добавление новых нуклонов всё менее и менее
увеличивает гравитационную энергию в расчёте на один нуклон.
В то же время добавление протонов в ядро с ростом массы и заряда ядра
приводит к заметному росту положительной электрической энергии, которая
начинает компенсировать изменение отрицательной гравитационной энергии. В
результате при 
для 
достигается максимум
на зависимости 
от 
, затем удельная энергия связи начинает уменьшаться с ростом . Таким образом, формулы для сильной гравитации и
электромагнитных сил и энергий позволяют не только описать равновесие нуклонов в
ядре, но и объяснить зависимость удельной энергии связи от массового числа. При
этом уменьшение массы атомных ядер по сравнению с общей массой нуклонов, из
которых состоит ядро, связывается нами с противоположностью потоков энергии,
необходимых для возникновения энергии связи, по сравнению со случаем обычного
гравитационного сжатия вещества.
Общая
теория относительности
Аксиоматика общей теории относительности (ОТО) связана с признанием гравитационного
поля как некоторой формы метрического поля, и с геометрическим отличием
искривлённого риманова пространства-времени от плоского пространства-времени
Минковского. В настоящее время ОТО является наиболее известной и разработанной
теорией гравитации. Основой теории можно считать уравнения Гильберта-Эйнштейна
для метрики:
, (20)
где 
− тензор Риччи,
− скалярная кривизна,
− метрический тензор,
− космологическая
постоянная,
− гравитационная
постоянная,
− скорость света,
− тензор плотности
энергии-импульса вещества,
− тензор плотности
энергии-импульса электромагнитного поля и других негравитационных полей.
Если пренебречь космологической постоянной, рассматривать метрику
вокруг неподвижного незаряженного однородного шара с плотностью его вещества 
и тензором 
, где 
есть 4-скорость, то в
сферических 4-координатах 
, метрический тензор как решение уравнения (20) имеет
следующие компоненты:
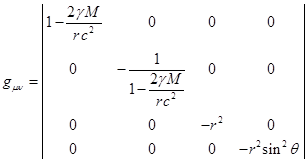. (21)
Это известное решение Шварцшильда для метрики вокруг
массивного точечного тела с массой 
, зависящее только от угла 
и от расстояния 
между притягивающим
центром и точкой наблюдения.
Уравнение движения ОТО для пробного тела возле притягивающей
его массы таково:
,
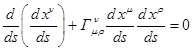(22)
где 
есть инвариантный
интервал,
− дифференциал
собственного времени пробного тела,
− 4-вектор сдвига
пробного тела,
− символ Кристоффеля,
выражающийся через метрический тензор и его производные по координатам.
Если с метрическим тензором (21) решить уравнение (22) для
временной компоненты , когда 
, получится следующее:
.
(23)
Умножим (23) на 
, где 
есть масса пробного
тела, и рассмотрим ситуацию на бесконечности. Здесь 
из-за больших значений
стремится к 1, а
дифференциал собственного времени приобретает тот же вид, что и в специальной
теории относительности: 
, где 
обозначает скорость
движения пробного тела на бесконечности. Тогда (23) переходит в равенство,
справедливое на бесконечности:
.
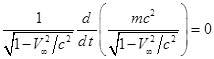В скобках данного равенства находится релятивистская энергия
тела с массой 
, двигающегося на бесконечности со скоростью . Следовательно, (23) можно трактовать как закон сохранения
энергии пробного тела в гравитационном поле (при свободном падении энергия
гравитационного поля переходит в кинетическую энергию, а сумма отрицательной
энергии поля и положительной кинетической энергии равна нулю). После умножения
(23) на и интегрирования получается
релятивистская энергия:
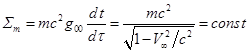. (24)
Согласно (24), при падении пробного тела на притягивающий центр
и изменении радиального расстояния 
изменяется как 
, так и дифференциал собственного времени по отношению к
дифференциалу координатного времени 
, но релятивистская энергия пробного тела остаётся
неизменной.
Предположим теперь, что частицы вещества пробного тела на
бесконечности были как-то распылены таким образом, что их скорость была вблизи нуля, а при их сближении с массивным телом
частицы столкнулись друг с другом. Если при столкновении частицы потеряют часть
своего общего момента импульса, и преобразуют часть своей энергии в тепловую
энергию столкновения 
, которая излучится из системы, то затем возможно стационарное
вращение вещества вокруг притягивающего центра. Условием для этого является
выполнение теоремы вириала, по которой модуль полной энергии системы должен
равняться излучённой из системы энергии: 
. В результате релятивистская энергия пробного тела,
падающего из бесконечности с нулевой начальной скоростью в гравитационном поле,
уменьшится на величину :
. (25)
Таким образом, в ОТО вещество массы , вращающееся в стационарном состоянии вокруг притягивающего
центра, должно уменьшать свою релятивистскую энергию за счёт вклада
отрицательной по величине полной энергии 
. Этот же вывод остаётся, если притягивающий центр возникает
за счёт коллапса вещества некоторого массивного облака, уменьшающего с течением
времени своё момент импульса посредством электромагнитного излучения.
Соотношение (25) по своему смыслу не совпадает с (3), в котором полная энергия 
не добавляется, а
вычитается из энергии покоя.
Ковариантная
теория гравитации
В отличие от общей теории относительности, ковариантная
теория гравитации (КТГ) основана на аксиомах лоренц-инвариантной теории
гравитации [6], [11], и является её ковариантным обобщением на искривлённое
риманово пространство-время. Гравитация в КТГ полагается не фиктивной
геометрической, а реальной физической силой, и может быть обоснована с помощью
теории гравитации Фатио-Лесажа. В КТГ вещество через 4-вектор плотности
импульса 
порождает
гравитационное поле с 4-потенциалом 
,
удовлетворяющим волновому уравнению в римановом пространстве-времени:
, (26)
где 
– скорость
распространения гравитации, близкая по значению к скорости света,
обозначает
4-даламбертиан,
есть тензор Риччи в
смешанных индексах,
− гравитационная
постоянная.
4-вектор плотности импульса определяется
произведением плотности вещества 
, находимой в системе покоя элемента вещества, на 4-вектор
скорости: 
. Если использовать приближение слабого поля и малых скоростей,
когда КТГ переходит в лоренц-инвариантную теорию гравитации, 4-вектор скорости
имеет вид:
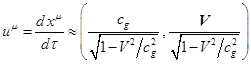. (27)
Выражение 4-вектора скорости (27) принято и в ОТО при 
в случае слабых полей
и малых скоростей. В римановом пространстве можно ввести [6] оператор дифференцирования
по собственному времени 
:
, (28)
где символом 
обозначен полный
дифференциал в искривлённом пространстве-времени,
есть ковариантная
производная.
Если с
помощью операции антисимметричного тензорного произведения ковариантного
оператора градиента на ковариантный 4-вектор потенциала 
образовать тензор напряжённостей гравитационного поля:
,
то с его помощью связь
между веществом и полем (26) становится такой:
.
(29)
Ковариантный 4-вектор
потенциала определяется так:
,
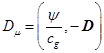где 
– скалярный потенциал,
– векторный потенциал.
Собственные свойства
напряжённостей гравитационного поля, не зависящие от вещественных источников,
задаются соотношением:
. (30)
Соотношения (29) и (30) являются записью уравнений гравитационного поля в
КТГ, пригодной в любой системе отсчёта.
Поле в свою очередь влияет на вещество, создавая
гравитационную силу. 4-вектор плотности гравитационной силы определяется
соотношением:
, (31)
где 
есть тензор плотности
энергии-импульса, конструируемый с помощью тензора напряжённостей гравитационного поля 
и равенств (29) –
(31). Наличие тензора 
выгодно отличает КТГ по
сравнению с ОТО, в которой точное выражение для тензора плотности
энергии-импульса гравитационного поля отсутствует.
Общее определение силы в КТГ осуществляется с помощью (28):
.
(32)
Электромагнитная сила определяется соотношением:
,
где 
– тензор напряжённостей электромагнитного поля,
– 4-вектор плотности
электромагнитного тока,
– плотность заряда в
системе отсчёта, в которой заряд покоится,
– тензор плотности
энергии-импульса электромагнитного поля.
Если есть только два фундаментальных поля, гравитационное и
электромагнитное, создающие силы, то уравнение движения элемента вещества
принимает вид:
. (33)
Как было показано в [11], уравнение движения в ОТО выводится
из (33) как частный случай.
С целью определения метрики пространства-времени используются
уравнения Гильберта-Эйнштейна [12]:
. (34)
В отличие от (20), в КТГ гравитационное поле наряду с
электромагнитным полем участвует в нахождении метрики, поэтому в правой части
(34) присутствует тензор плотности энергии-импульса гравитационного поля 
. Тензор плотности энергии-импульса вещества 
в КТГ конструируется
таким образом, чтобы ковариантная производная от этого тензора, взятого с
контравариантными индексами, давала плотность силы (32): 
. Если взять ковариантную производную от (34), левая часть
обращается в нуль вследствие свойств метрического тензора. Отсюда снова
вытекает равенство для плотности сил (33):
.
Решение уравнения для метрики (34) вблизи незаряженного
покоящегося шара даёт компоненты метрического тензора в сферических
4-координатах 
, [6] :
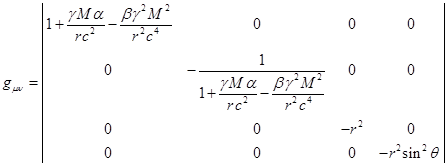. (35)
Коэффициенты 
и 
в (35) из уравнений
(34) не определяются и должны уточняться для каждой конкретной системы тел.
Используя метрический тензор (35), можно найти решение
уравнения движения (33) для временной компоненты при 
. Для случая слабого поля и при постоянной плотности 
элемента вещества
получается:
, или 
. (36)
На бесконечности 
стремится к 1, 
, где 
обозначает скорость
движения пробного тела на бесконечности, и 
. Пусть 
, тогда после умножения на 
(36) можно записать
так:
. (37)
Согласно (37) вещество, имевшее на бесконечности
релятивистскую энергию , при падении в гравитационном поле увеличивает свою энергию
на величину, равную модулю потенциальной энергии поля 
. Хотя в КТГ имеется отличие выражений и 
от соответствующих
выражений в ОТО, в (37) выполняется приблизительное равенство между модулем
изменения потенциальной энергии гравитационного поля и изменением кинетической
энергии движения вещества.
Если для данной системы справедлива теорема вириала, для
выполнения которой необходимо уменьшение момента импульса падающего вещества,
излучение из системы энергии 
и увеличение
кинетической энергии вещества на величину 
, то релятивистская энергия будет равна:
, (38)
где 
есть полная энергия
массы 
в гравитационном поле.
В случае, если гравитация создаётся некоторой стационарной
системой с массой , то энергия 
в (38) будет характеризовать
изменение релятивистской энергии системы, произошедшее за счёт действия
гравитационного поля, взаимодействия частиц вещества и излучения из системы.
Соотношение (38) имеет такой же вид, что и (3), где перед полной энергией 
также имеется
отрицательный знак. Из изложенного видно, что различие результатов КТГ и ОТО
возникает вследствие различия уравнений движения (33) и (22).
Выводы
Рассмотрев некоторые случаи связи массы и энергии, мы сделали
предположение о том, что если система теряет энергию в виде излучения или
выполнения работы над окружающими телами, то полная энергия частиц системы
должна вычитаться из энергии покоя частиц, составляющих систему. Для
фундаментальных сил полная энергия системы отрицательна, что приводит к
увеличению массы системы частиц по сравнению с суммой масс частиц по
отдельности. В частности, масса звезды в соответствии с ковариантной теорией
гравитации может оказаться больше суммарной массы разрозненного вещества
звезды. Это подтверждается и в статье [13]. В другом случае, когда для
образования системы требуется добавить в неё энергию или совершить над ней
работу, полную энергию частиц системы следует добавлять к энергии покоя частиц,
составляющих систему. В ряде случаев это приводит к уменьшению релятивистской
энергии и массы системы (примером является образование атомных ядер из
нуклонов).
Наши предположения в сущности противоположны стандартной
точке зрения, по которой подходящая по форме полная энергия всегда просто
добавляется к энергии покоя частиц, составляющих систему. Как для звёзд
согласно общей теории относительности, так и для атомных ядер это приводит к
уменьшению их массы по сравнению с массой покоя составляющих эти объекты
частиц, а при нагревании тела его масса должна расти. По видимому, в
сложившейся ситуации требуются дополнительные подтверждения того, увеличиваются
ли в действительности, или уменьшаются инертные, а также гравитационные массы
массивных составных объектов по сравнению с суммой масс составных частей.
При этом следует учесть следующее. Если подсчитать долю
энергии гравитационной связи по отношению к энергии покоя вещества для типичной
нейтронной звезды, то эта доля может достичь 6 %. На такую же величину должна
увеличиться (или уменьшиться) гравитационная масса звезды, а значит и сила,
действующая на пробное тело возле звезды. С другой стороны, сила, действующая
на тело, согласно теории гравитации Фатио-Лесажа, зависит в том числе и от плотности
этого тела. Для двух тел малой плотности достаточно точно выполняется закон
Ньютона для гравитационной силы, но когда плотность вещества взаимодействующих
тел достигает плотности нейтронных звёзд, сила уменьшается по величине и равна
26 % от силы Ньютона [6]. Как видно, эффект изменения гравитационной массы
может зависеть не только от полной энергии тел, но и от других параметров, что
может усложнить экспериментальную проверку теории.
Список использованных источников
1.
Болотовский Б. М. Оливер Хевисайд. — М.: Наука,
1985. — 254 с.
2.
Poincaré H. La théorie de
Lorentz et le principe de réaction
(фр.)
// Archives
néerlandaises des sciences exactes et naturelles. — 1900. — Vol. 5. — P. 252—278.
3. Einstein, A. (1905), "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?", Annalen der Physik 18: 639–643, Bibcode 1905AnP...323..639E, doi:10.1002/andp.19053231314. See also the English translation.
4.
Федосин С.Г. Энергия, импульс, масса и скорость
движущегося тела. vixra.org, 12 июня 2011.
5.
Федосин С.Г. Физика и философия
подобия от преонов до метагалактик.
Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN
5-8131-0012-1.
6.
Федосин С.Г. Физические теории и бесконечная вложенность материи.
Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
7.
2011 CODATA recommended value .
8.
WolframAlpha,
computational knowledge engine.
9.
Федосин С.Г. Комментарии к книге: Физические
теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21,
Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
10. Fedosin
S.G. Model of Gravitational Interaction in the Concept of
Gravitons. Journal of Vectorial Relativity, Vol. 4, No.
1, March 2009, P.1–24.
11. Федосин С.Г. Общая теория относительности, метрическая теория относительности и
ковариантная теория гравитации. Аксиоматизация и критический анализ. vixra.org, 26 марта
2011.
12. Fedosin S.G. The
Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, February 2012, Vol. 35, No. 1, P. 35 – 70.
13. Fedosin S.G. The
Hamiltonian in covariant theory of gravitation.
vixra.org, 22 May 2012.
Источник:
http://sergf.ru/nv.htm