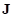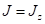International Frontier Science
Letters, Vol. 15, pp. 9-14 (2020). https://doi.org/10.18052/www.scipress.com/IFSL.15.9
О зависимости релятивистского момента
импульса однородного шара от радиуса и скорости углового вращения
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь,
614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
В рамках специальной теории
относительности в элементарных функциях выводится формула для определения
релятивистского момента импульса вращающегося идеального однородного шара. Момент
инерции такого шара оказывается нелинейной функцией от угловой скорости
вращения. Применение указанной формулы к нейтронной звезде PSR
J1614–2230 показывает, что момент импульса звезды за счёт релятивистских
поправок увеличивается в десять раз по сравнению с нерелятивистской формулой. Для
протона и нейтронной звезды
PSR J1748-2446ad вычисляются скорости движения их поверхности, достигающие
величины порядка 30% и 19% от скорости света, соответственно. С помощью формулы для релятивистского момента импульса
однородного шара нетрудно получить формулу для момента импульса тонкой
сферической оболочки, в зависимости от её толщины, радиуса, плотности массы и
угловой скорости вращения. В результате, рассматривая сферическое тело
состоящим из множества таких оболочек, становится возможным точно находить его
момент импульса как сумму моментов импульса всех оболочек тела. Приводятся два
выражения для максимально возможного момента импульса шара, исходя из вращения
поверхности шара со скоростью света, и исходя из условия целостности
гравитационно-связанного тела при балансе гравитационной и центростремительной
сил. Сравнение с результатами общей теории относительности показывает различие в
моменте импульса порядка 25% для экстремальной чёрной дыры Керра.
Ключевые слова: релятивистский момент импульса; момент
инерции; нейтронная звезда.
On the dependence of the relativistic angular momentum of a uniform ball
on the radius and angular velocity of rotation
Sergey G.
Fedosin
PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia
E-mail:
fedosin@hotmail.com
In the framework of the special theory of relativity, elementary
formulas are used to derive the formula for determining the relativistic
angular momentum of a rotating ideal uniform ball. The moment of inertia of
such a ball turns out to be a nonlinear function of the angular velocity of rotation.
Application of this formula to the neutron star PSR J1614-2230 shows that due
to relativistic corrections the angular momentum of the star increases tenfold as
compared to the nonrelativistic formula. For the proton and neutron star PSR
J1748-2446ad the velocities of their surface’s motion are calculated, which
reach the values of the order of 30% and 19% of the speed of light,
respectively. Using the formula for the relativistic angular momentum of a uniform
ball, it is easy to obtain the formula for the angular momentum of a thin
spherical shell depending on its thickness, radius, mass density, and angular
velocity of rotation. As a result, considering a spherical body consisting of a
set of such shells it becomes possible to accurately determine its angular
momentum as the sum of the angular momenta of all the body’s shells. Two
expressions are provided for the maximum possible angular momentum of the ball based
on the rotation of the ball’s surface at the speed of light and based on the condition
of integrity of the gravitationally bound body at the balance of the
gravitational and centripetal forces. Comparison with the results of the general
theory of relativity shows the difference in angular momentum of the order of
25% for an extremal Kerr black hole.
Keywords: relativistic angular momentum; moment of inertia; neutron star..
В
общей теории относительности момент импульса шара может быть вычислен с помощью
метрики [1], поскольку необходимо учесть как действие гравитации, так и
центростремительного ускорения, изменяющих метрические свойства объёма шара. В
специальной теории относительности в приближении слабого вращения влиянием метрики в первом приближении можно пренебречь.
Момент
импульса идеального однородного шара в классической механике вычисляется по
формуле:
, (1)
где
есть плотность массы
вещества шара, 
–
угловая скорость вращения, 
–
радиус шара, 
–
масса шара.
Однако
формула (1) не учитывает релятивистский эффект зависимости импульса от скорости
для каждой из частиц шара, так что (1) пригодно лишь при малых скоростях
вращения. Согласно специальной теории относительности, в движущемся с
постоянной линейной скоростью теле плотность массы увеличивается
пропорционально фактору Лоренца 
, где 
–
скорость тела, 
–
скорость света.
Одновременно с этим объём тела уменьшается
обратно пропорционально фактору Лоренца, как следствие Лоренцевского сокращения
длины. В результате масса тела как произведение
плотности массы на объём остаётся неизменным. Это же относится и к элементу
массы 
.
В рассматриваемом случае элемент массы шара движется по окружности вращения, а не по прямой линии. Таким образом наши расчёты будут ограничены той точностью, с которой специальная теория относительности аппроксимирует вращение тел, а инерциальные системы отсчёта аппроксимируют вращающиеся неинерциальные системы отсчёта, в которых возникает ускорение вращения.
Попробуем
для начала вычислить релятивистский момент импульса шара в декартовых
координатах 
. В этих координатах элемент объёма неподвижного однородного
шара определяется формулой 
. Умножая элемент объёма на плотность массы 
, находим элемент массы шара:
. Предположим, что шар вращается с угловой скоростью 
относительно оси 
неподвижной
системы координат с началом в центре шара.
Пусть некоторый элемент массы находится на
расстоянии 
от центра шара и
имеет релятивистский импульс 
, при этом линейная скорость движения элемента массы 
определяется
векторным произведением угловой скорости 
на радиус-вектор 
.
Поскольку вектор направлен вдоль оси , лишь две компоненты линейной скорости не равны нулю: 
. Для вычисления момента импульса элемента массы необходимо
векторно умножить радиус-вектор на импульс: 
. Затем следует проинтегрировать 
по всем элементам
массы шара, чтобы найти полный момент импульса 
. Компоненты 
и 
пропорциональны 
и 
, соответственно, так что после интегрирования по всему
объёму шара компоненты 
и 
обнуляются.
У вектора остаётся лишь одна компонента 
, направленная вдоль оси , и для величины этого вектора 
с учётом зависимости от
координат фактора Лоренца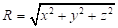 
находим:
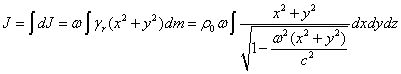. (2)
Подставим
пределы интегрирования в интеграле по объёму (2) и проинтегрируем по переменной
:
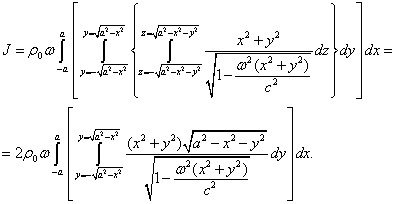(3)
По
всей видимости, интеграл по переменной 
в (3) относится к эллиптическим
интегралам и не сводится к элементарным функциям, что затрудняет его вычисление.
Соответственно, теряется наглядность в предсказании зависимости момента
импульса 
от угловой скорости,
массы или радиуса шара.
Тем
не менее вычисление релятивистского момента импульса шара возможно с помощью элементарных
функций. Мы покажем это в следующем разделе.
2.
Вычисление релятивистского момента импульса шара
В цилиндрической системе координат 
элемент объёма неподвижного однородного шара определяется
формулой 
, а элемент массы шара будет:
.
Текущая координата
направлена
перпендикулярно как к оси вращения, так и к скорости . Для релятивистского момента импульса элемента массы шара
можно записать: 
. Рассечём шар перпендикулярно оси на множество
параллельных слоёв толщиной 
и вычислим момент
импульса 
одного такого слоя,
имеющего некоторый максимальный радиус 
. Учитывая, что 
, 
, имеем:
(4)
Теперь
следует проинтегрировать (4) по всем слоям шара, то есть по переменной 
. Если радиус шара равен , можно интегрировать по переменной от нуля до , то есть по одной полусфере,
а затем увеличить результат в два раза, чтобы учесть вторую полусферу.
Внутри верхней полусферы радиус 
произвольного слоя связан
с переменной соотношением: 
. Это соотношение можно подставить в (4) и затем
проинтегрировать по всем слоям:
.
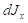В результате получается следующее:
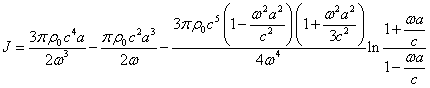. (5)
При малых угловых скоростях вращения 
можно разложить
логарифм в (5) до членов, содержащих в знаменателе множитель 
. Это даёт стандартный момент импульса шара и добавку первого
порядка:
.
(6)
Другой предельный случай получится, если полагать,
что поверхность на экваторе шара движется за счёт вращения со скоростью,
достигающей скорости света. В (5) это соответствует тому, что отношение 
устремляется к
единице. Если учесть, что
,
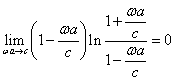то в (5) исчезает третий член с логарифмом,
и для предельного момента импульса шара при 
получается:
. (7)
В рамках специальной теории относительности
ни одно сферическое тело не может достичь момента импульса, равного (7). Для
гравитационно-связанных тел существует более мягкое условие на максимальную
скорость вращения, связанное с устойчивостью вещества на экваторе, где линейная
скорость имеет наибольшую величину. Здесь центробежное ускорение не должно
превышать ускорения от силы гравитации, что приводит к неравенству: 
. Подставляя данную угловую скорость в (5) и в (6), можно
оценить максимальный момент импульса гравитационно-связанных тел, зная лишь их
массу и радиус.
В общей теории относительности экстремальная
чёрная дыра Керра с наибольшим возможным вращением имеет момент импульса 
и радиус поверхности
событий 
. Если подставить 
в (7), то получится 
. Таким образом, в общей теории относительности предельный
момент импульса экстремальных объектов увеличивается на 25 % по сравнению с
результатом специальной теории относительности.
3. Расчёт момента импульса нейтронной
звезды и протона
Полученные результаты являются полезными для
оценки момента импульса и момента инерции таких быстровращающихся объектов, как
нейтронные звёзды и нуклоны. Момент инерции может быть определён как отношение
момента импульса к угловой скорости вращения: 
. Масса однородного шара зависит от плотности массы и
объёма шара: 
. Подставляя это в (5), получаем формулу для момента инерции
однородного шара, вращающегося с угловой скоростью 
:
. (8)
Используем
(8) для оценки момента инерции пульсара PSR J1614–2230,
для которого согласно [2] известны угловая скорость
вращения 
рад/с, радиус 
км и масса 
, где 
есть масса Солнца. Так
как для этого пульсара 
, поверхность его экватора движется со скоростью
порядка 8,5% от скорости света. С этими данными из (8) следует, что для пульсара
момент инерции равен 
кгˑм2,
а момент импульса достигает величины 
кгˑм2/с . В то же время, если
бы мы делали расчёт по классической формуле 
, то момент импульса получился бы равным 
кгˑм2/с . Как видно, в данном
случае релятивистская формула для момента импульса даёт в десять раз большее
значение, чем простая формула из классической механики. Для звезды однако
следует учесть, что плотность её массы увеличивается в центре, где она превышает
среднюю плотность приблизительно в 1,5 раза [3]. В результате момент импульса
звезды должен быть меньше, чем величина 
кгˑм2/с , вычисленная для
однородного шара при его релятивистском вращении.
В квантовой механике известно, что спин
протона равен 
, где 
есть постоянная
Дирака. Предположим, что эта величина равна моменту импульса протона 
, и оценим, как вращается протон в этом случае. Если
обозначить 
, где 
есть радиус протона, то
из (8) следует:
.
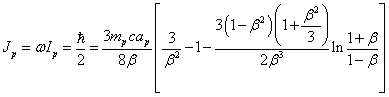(9)
В (9) постоянная Дирака и масса протона 
хорошо известны, а в
качестве радиуса протона используем значение 
м согласно [4]. В таком случае (9) превращается в уравнение
для 
. Решением этого уравнения является значение 
, откуда следует значение угловой скорости вращения протона 
рад/с. При этом скорость вращения поверхности протона
достигает 30% от скорости света.
4. Заключение
Используя разбиение шара на множество
параллельных слоёв, мы находим в (5) формулу для релятивистского момента
импульса однородного шара, выраженную в элементарных функциях. Согласно (6),
при малых угловых скоростях вращения релятивистская
поправка к стандартному моменту импульса растёт пропорционально 
, то есть пропорционально кубу скорости вращения. При
достаточно больших скоростях вращения момент импульса изменяется как логарифмическая
функция. Предельный момент импульса шара достигается тогда, когда точки
поверхности на экваторе шара двигаются со скоростью света, при этом момент
импульса выражается формулой (7).
Формулу (5) можно использовать для
вычисления релятивистского момента импульса тонкой сферической оболочки
толщиной 
: 
, где 
есть момент импульса
шара с радиусом 
. При этом в данный шар вложен шар с уменьшенным радиусом 
и моментом импульса 
. Таким образом момент импульса 
оболочки становится
функцией радиуса оболочки, угловой скорости её вращения, плотности массы и
толщины этой оболочки.
С учётом этого, любое вращающееся
сферическое тело можно разделить на множество сферических оболочек, каждая из
которых имеет свой радиус, угловую скорость вращения и плотность массы, и
соответственно, свой момент импульса . Для вычисления момента импульса сферического тела
необходимо лишь просуммировать моменты импульса всех оболочек тела. Точность
результата будет зависеть от количества используемых оболочек и точности, с
которой известно распределение плотности массы и угловой скорости вращения
внутри тела.
Полученные результаты мы используем для вычисления момента импульса и момента инерции нейтронной звезды PSR J1614–2230. Оказывается, что релятивистский момент импульса получается в десять раз больше, чем момент импульса согласно нерелятивистской формуле.
Для протона мы определяем соответствующую
угловую скорость вращения, исходя из его квантового спина. При этом скорость
движения экваториальных точек протона достигает 30% от скорости света. Что
касается звезды PSR J1614–2230, скорость движения её экваториальных точек достигает
8,5% от скорости света. Добавим, что согласно [5] самым быстровращающимся
пульсаром на сегодняшний день является PSR J1748-2446ad с угловой скоростью
вращения 
рад/с. Если считать, что по массе и размерам он является
аналогом PSR J1614–2230, то при предполагаемом радиусе 
км относительная скорость
движения на поверхности звезды могла бы достичь величины 
. В этом случае звезда могла бы вращаться со скоростью на
экваторе порядка 19% от скорости света, что уже сравнимо с вращением
поверхности протона.
Список использованных источников
1.
Molina A. and Ruiz E.
An approximate global solution of Einstein’s equations for a differentially
rotating compact body. General Relativity and Gravitation, Vol 49,no 10, pp.
135 (2017). https://doi.org/10.1007/s10714-017-2297-5.
2.
Demorest P. B., Pennucci
T., Ransom S.M., Roberts M.S.E., Hessels J.W.T. A two-solar-mass neutron star measured using Shapiro
delay. Nature. Vol. 467 (7319), pp. 1081-1083 (2010). doi:10.1038/nature09466.
3. Fedosin S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics,
Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593;
Оценка физических параметров планет и звёзд в
модели гравитационного равновесия.
4. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic
Journal, Vol. 35, No.
4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451;
Радиус протона в самосогласованной модели.
5.
Hessels
J.W.T., Ransom S.M., Stairs I.H., Freire P.C.C., Kaspi
V.M., Camilo F. A Radio Pulsar Spinning at 716 Hz. Science. Vol. 311 (5769), pp. 1901-1904 (2006). doi:10.1126/science.1123430 .
Источник: http://sergf.ru/dr.htm