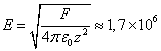In English

 

 

Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 265, 106374 (2024). https://doi.org/10.1016/j.jastp.2024.106374  

 

Электронно-ионная модель шаровой и чёточной молнии

 

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail: fedosin@hotmail.com

 

На основе электронно-ионной модели вычисляются параметры шаровой и чёточной молний. Модель позволяет оценить максимальный размер шаровой молнии, её энергосодержание, электрический заряд и магнитное поле, определить условия равновесия между положительно заряженными ионами, расположенными внутри, и внешней оболочкой, содержащей быстро движущиеся электроны. Даётся объяснение тому факту, что внутри шаровой молнии наблюдаются оболочки, отличающиеся друг от друга цветом свечения. Модель описывает структуру не только шаровой, но и чёточной молнии. Долговременная стабильность чёточной молнии связывается с равновесием соседних чёток под действием магнитной силы их притяжения и электрической силы отталкивания, превышающих по величине силу напора ветра.

Ключевые слова: шаровая молния; чёточная молния; электронно-ионная модель.

 

Electron-ion model of ball and bead lightning

 

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

E-mail: fedosin@hotmail.com

 

Abstract: Based on the electron-ion model, parameters of ball and bead lightning are calculated. The model allows us to estimate maximum size of ball lightning, its energy content, electric charge and magnetic field, to determine equilibrium conditions between positively charged ions located inside and outer shell containing rapidly moving electrons. An explanation is given to the fact that shells are observed inside ball lightning that differ from each other in color of glow. The model describes structure of not only ball lightning, but also bead lightning. The long-term stability of bead lightning is associated with the balance of neighboring beads under action of magnetic force of their attraction and electric force of repulsion, which exceed in magnitude the force of wind pressure.

Keywords: ball lightning; bead lightning; electron-ion model.

 

1. Введение

Общеизвестна связь между появлением обычных (normal linear lightning) и шаровых молний (ball lightning), а также появлением обычных (normal lightning) и чёточных молний (bead lightning). По статистике, интенсивность наблюдений шаровых молний (ШМ) (ball lightning) (BL) очень хорошо повторяет распределение грозовой активности в течение суток и частоту гроз по месяцам в течение года практически во всех странах. Это же самое относится и к чёточным молниям, которые обычно возникают как следствие трансформации в них обычных молний [1-2].

В модели, описанной в [3-4], делается вывод о том, что ШМ и чёточные молнии появляются в ионизованном воздухе в канале линейной молнии и в момент прекращения тока в молнии быстро увеличивают свой размер под действием волны расширения, направленной радиально по отношению к каналу. После этого положительные ионы, расположенные в основном в центре ШМ, и отрицательные ионы постепенно аннигилируют, уменьшая тем самым электрическое поле внутри ШМ. Предполагается, что частицы почвы (particles from the soil), захватываемые посредством электрического поля, попадают внутрь ШМ и обеспечивают её последующее свечение, воспламеняясь в очень горячем воздухе, находящемся в канале молнии. Цвет свечения в этом случае зависит от состава частиц почвы и количества металлов в этих частицах. Эти же частицы могут быть ответственными за искры, появляющиеся рядом с поверхностью ШМ. Несмотря на то, что фрагментация линейной молнии на отдельные сегменты связывается с пинч-эффектом, в данной модели отсутствует расчёт действия магнитного поля на структуру и конфигурацию токов и полей внутри возникающих ШМ и сегментов чёточной молнии. Кроме этого, возникает трудность с объяснением свечения тех ШМ, которые, согласно наблюдениям, возникают внутри дождевых облаков, где нет частиц почвы.

В некоторых моделях внутри ШМ предполагается магнитное поле, возникающее от движения заряженных частиц ионизованной плазмы [5-6]. В [7] предполагается, что ШМ могла бы быть плазмоидом, содержащим в себе бессиловое магнитное поле, в котором все электрические токи в плазме параллельны силовым линиям магнитного поля. Однако одного лишь магнитного поля недостаточно для устойчивой конфигурации ШМ, требуются какие-то дополнительные силы [8-9].

Существует множество моделей, описывающих внутреннюю структуру ШМ. Например, в [10-11] развивается протон-электронная модель, согласно которой в оболочке ШМ содержатся протоны с высокой энергией (high-energy protons), а электроны находятся в центре ШМ. Как протоны, так и электроны находятся во вращательном движении, создавая магнитное поле ШМ. За счёт магнитного поля возникает сила Лоренца, которая вместе с электрической силой поддерживает устойчивое вращение заряженных частиц внутри ШМ.

Особенностью модели в [12] является то, что ядро шаровой молнии содержит электроны и почти полностью ионизованный воздух, причём электроны и ионы находятся в колебательном движении друг относительно друга. Электроны колеблются в основном в радиальном направлении. Ядро окружено слоем нагретого воздуха, изолирующего его от остальной атмосферы. В этой модели предполагается, что электроны в ядре шаровой молнии могут испускать электромагнитное излучение в рентгеновском и гамма-диапазонах, Недостатком обеих моделей [10-11] и [12] является то, что отсутствует описание процессов, которые могли бы привести к предлагаемой структуре ШМ, к разделению молекул воздуха на требуемую композицию частиц с соответствующим движением этих частиц.

В [13-14] указывается, что до сих пор нет удовлетворительной модели, описывающей все наблюдаемые свойства и механизм образования чёточной молнии.

В связи с этим, в данной работе мы представляем общий механизм образования и внутреннее устройство как ШМ, так и чёточной молнии, на основе электронно-ионной модели согласно [15-19]. Конфигурация зарядов в этой модели такова, что движущиеся электроны и ионы взаимодействуют друг с другом посредством как электрического, так и магнитного полей, обеспечивая долговременную стабильность ШМ.

Нашей целью является не только качественные выводы, но и количественные расчёты основных параметров ШМ и чёточной молнии в их равновесном состоянии. Основное внимание будет уделено общей картине и согласованности результатов с физикой явлений и с результатами наблюдений.

В Разделах 2.1 и 2.2 будут описаны механизмы возникновения и параметры ШМ, а Раздел 3 полностью посвящён описанию возникновения чёточной молнии с вычислением её физических параметров. При обсуждении результатов в Разделе 4.1 мы сравним свойства ШМ в электронно-ионной модели с результатами наблюдений ШМ, а в Разделе 4.2 сравним электронно-ионную модель с результатами экспериментов и теоретических исследований.

 

2. Электронно-ионная модель шаровой молнии

2. 1. Возникновение шаровой молнии

В рамках электронно-ионной модели природная ШМ является непосредственным следствием линейной молнии (linear lightning), когда грозовое облако (cumulonimbus cloud or thunderhead) разряжается на землю или на соседние облака. В модели обычного грозового облака, описанной в [20] и подтверждаемой наблюдениями, верхняя часть облака заряжена положительно, а нижняя часть облака заряжена отрицательно. Если не считать многочисленных разрядов внутри облаков, линейные молнии наблюдаются обычно между нижней частью грозовых облаков и землёй, и такие молнии переносят на землю отрицательное электричество. По мере развития грозовой ячейки (thunderstorm cell) нижняя часть облака может разрядиться, а положительный заряд в верхней части облака может сохраниться. Этот положительный заряд может стать причиной молний, в которых электроны движутся не от облака к земле, а в обратном направлении, от земли к облаку.

В принципе, оба типа молний, хотя и отличаются направлением тока в них, способны приводить к возникновению ШМ. В случае, когда электроны в линейной молнии движутся к положительно заряженному облаку, вначале под действием сильного электрического поля в сторону облака от земли испускаются так называемые ступенчатые лидеры (step leaders), создающие в воздухе проводящие каналы (conducting channels), наполненные электронами. Большинство этих каналов так и не соединится с облаком, скорее часть из них соединится друг с другом и с основным каналом молнии. При дополнительных условиях подобная разветвлённая конфигурация ветвей с электронами в них оказывается благоприятной для возникновения ШМ.

В другом случае, когда электроны в молнии движутся от отрицательно заряженной части облака к земле, ступенчатый лидер движется к земле скачками длиной порядка 50 м, со скоростью порядка 1/6 скорости света и с остановками около 50 мкс [20]. При расстоянии между лидером и землёй около 100 метров, от земли в ионизированном воздухе в сторону лидера начинают подниматься положительные заряды, создающие проводящие каналы. В результате лидер может разветвиться и соединиться с этими каналами, и первые из этих соединившихся каналов пропустят через себя наибольший ток и станут заметны за счёт яркого свечения.

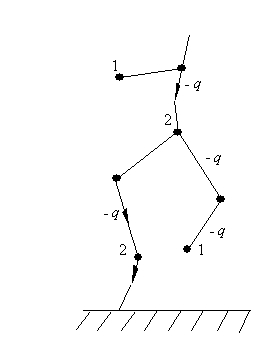
Механизм, в котором ШМ возникает в случае, когда вторичные ветви линейной молнии образуют почти замкнутую круговую конфигурацию, описан в [15-17], [19]. Если в основном канале молнии начинается электрический ток, то электроны, имеющиеся во вторичной ветви, под действием электрического поля начинают перемещаться в основной канал. Благодаря круговой конфигурации вторичной ветви движение электронов создаёт магнитное поле, фиксирующее положительные ионы внутри ветви. При внезапной остановке тока в основном канале ток электронов во вторичной ветви может замкнуться сам на себя, образуя внешнюю оболочку рождающейся ШМ. Такая оболочка удерживается положительным зарядом ионов внутри ШМ. Описанная ситуация иллюстрируется на Рисунке 1.

 

 

a)                                                                 b)

 

 

Другой способ образования ШМ может быть связан с пинч-эффектом, вследствие которого канал тока молнии может быть пережат магнитными силами. Пока электроны движутся в канале молнии, они создают сильное магнитное поле, при этом магнитные силовые линии окружают канал и имеют форму окружностей. Некоторые электроны и ионы рядом с каналом молнии, если их скорости направлены вдоль магнитных линий, движутся по окружностям вокруг канала. В случае, когда движение электронов внутри канала молнии прекращается, вращательное движение внешних электронов вокруг канала может сохраниться, если имеется сила, удерживающая электроны от разлёта. Такой силой может быть электрическая сила от положительных ионов, находящихся внутри внешней оболочки из электронов. Пинч-эффект наиболее ярко проявляется при трансформации обычной молнии в чёточную молнию.

Согласно электронно-ионной модели. ШМ имеет осесимметричную конфигурацию с сильным поверхностным током электронов в тонкой внешней оболочке. Положительные ионы могут быть при атмосферном давлении в очень горячем воздухе внутри ШМ, оставшемся после удара линейной молнии. Быстро движущиеся во внешней оболочке электроны генерируют магнитное поле, которое удерживает ионы на орбитах внутри ШМ. Такая ШМ будет стабильна до тех пор, пока в ней сохраняется равновесная конфигурация токов ионов и электронов, изолированных друг от друга.

В [21-22] можно найти, что длина свободного пробега электронов в воздухе при стандартных условиях для случая упругих столкновений с нейтральными молекулами (electron mean free path with respect to elastic collisions with neutrals in air under standard temperature and pressure) находится в пределах 1 – 1,7 мкм. При скорости электронов порядка  м/с это даёт время  с как оценку того времени, в течение которого происходит одно столкновение свободного электрона с молекулой воздуха. Относительное уменьшение кинетической энергии электрона при одном упругом столкновении зависит от соотношения масс электрона и молекулы и оценивается величиной . Это приводит к тому, что после ряда столкновений приблизительно через  с электрон теряет свою энергию движения и соединяется с какой-нибудь молекулой, образуя ион. В таком случае, каким же образом сферические токи электронов могут долговременно существовать, находясь во внешней оболочке ШМ?

Для ответа на этот вопрос учтём, что электроны в момент образования ШМ приобретают значительную энергию посредством электрического и магнитного полей вблизи канала и ветвей линейной молнии. За счёт этой энергии электроны, быстро движущиеся во внешней оболочке ШМ, осуществляют непрерывную ионизацию молекул окружающего воздуха, порождая всё новые потоки электронов, замещающие потери электронов. С другой стороны, общий положительный заряд ШМ действует на положительно заряженные ионы воздуха так, что выталкивает их из внешней оболочки с электронами, а затем отталкивает эти ионы от поверхности ШМ. Ввиду большой плотности тока во внешней оболочке, электроны создают в этой оболочке своё собственное динамическое давление, противодействующее проникновению ионов и молекул воздуха в эту оболочку. Как следствие, электроны при движении во внешней оболочке не часто сталкиваются с ионами и долго не теряют свою энергию.

Большая напряжённость электрического поля ШМ способствует дополнительной ионизации нейтральных молекул воздуха. Что касается взаимодействия электронов оболочки с ионами воздуха внутри ШМ, то это взаимодействие осуществляется в основном через магнитное поле, вынуждающее ионы вращаться вокруг общей оси вращения. Фиксация ионов магнитным полем препятствует их взаимодействию с электронами оболочки. Хотя на ионы действует ещё радиальная электростатическая сила объёмного положительного заряда ШМ, суммарное давление этой силы на оболочку ослаблено из-за связи ионов с магнитным полем, так что сила между объёмным зарядом внутри ШМ и электронами во внешней оболочке может удерживать ШМ в равновесии. Тем самым ионы воздуха внутри ШМ достаточно слабо уменьшают энергию движения этих электронов. Всё это эффективно уменьшает количество взаимодействий электронов в оболочке с ионами и молекулами воздуха и потерю энергии электронов в единицу времени, что увеличивает время жизни ШМ до наблюдаемых значений вплоть до десятков секунд.

Электроны во внешней оболочке отталкиваются сами от себя, но благодаря электрическому притяжению от положительных ионов, находящихся внутри ШМ, электроны не рассеиваются и удерживаются в этой оболочке. Кроме этого, притяжение ионов является основной частью центростремительной силы, необходимой для удержания электронов при их вращении во внешней оболочке [16-17].

Данная относительно устойчивая конфигурация позволяет объяснить наблюдаемое время жизни ШМ, существенно превышающее время жизни однородной ионно-электронной плазмы при атмосферном давлении. Электронная оболочка эффективно изолирует нагретый до высокой температуры воздух внутри ШМ, замедляя перенос энергии в окружающую среду.

 

2.2. Физические свойства шаровой молнии

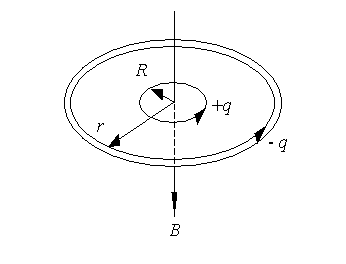
Электрические токи и магнитное поле внутри ШМ показаны на Рисунке 2.

 

 

 

Внутри ШМ можно найти оболочки, где тепловая скорость тех или иных ионов выравнивается со скоростью вращения этих ионов в магнитном поле [17]. В этом месте можно приравнять центростремительную силу, действующую на вращающиеся ионы, и магнитную силу Лоренца, действующую на ионы в экваториальной плоскости, перпендикулярной магнитному полю:

 

,                                                           (1)

 

где  – массы, скорости движения и радиусы вращения ионов,

 - элементарный электрический заряд,

 - индукция магнитного поля.

 

В общем случае вместо (1) следовало бы записать систему векторных уравнений движения нейтральных и заряженных частиц (молекул воздуха, ионов и электронов) в электромагнитном поле с учётом векторного поля давления и векторного поля ускорений аналогично [23-24]. Другой подход подразумевает использование уравнений гидродинамики и магнитогидродинамики (equations of hydrodynamics and magnetohydrodynamics) [5], [21] с поправками на различные эффекты от действия электромагнитного поля на вещество. Вместо этого мы выделяем главные члены уравнений, чтобы получить оценки физических величин в первом приближении.

С целью упрощения расчётов в (1) предполагается, что большинство ионов ионизированы однократно и потому их заряд равен элементарному электрическому заряду. Действительно, согласно [25], в наблюдаемых ШМ обнаруживаются однократно ионизованные атомы кислорода и азота, а также двукратно ионизованный азот.

С другой стороны, заряженные частицы могут беспрепятственно двигаться вдоль линий магнитного поля, проходящих вдоль оси ШМ от одного полюса к другому. Следовательно, внутри ШМ возможны ещё такие оболочки, где встречаются упорядоченные взаимно перпендикулярные ионные потоки, что сопровождается сильным трением в газе и соответствующим выделением энергии в виде излучения. Так как воздух состоит из нескольких газов, то при высокой температуре возникают положительные ионы различных масс и разной степени ионизации. Эти ионы будут иметь несовпадающие тепловые скорости и радиусы вращения в магнитном поле. В результате в ШМ могут возникать вложенные друг в друга светящиеся оболочки различного цвета и яркости, в зависимости от состава ионов и от скорости перехода кинетической энергии в излучение при столкновениях ионов в той или иной оболочке.

Приведём наши расчёты параметров ШМ с общим радиусом  см и радиусом выделенной оболочки  см, аналогичной описанной в [26-27]. С целью упрощения будем считать, что заряды и токи в основном сконцентрированы вблизи экваториальной плоскости или имеют цилиндрическую симметрию, а ионы однозарядны. Согласно [17], электронный ток  во внешней оболочке и магнитное поле  этого тока, действующее на ионы, можно выразить через количество электронов  и их скорость  при известной температуре :

 

.                                                                   (2)

 

.                                                                   (3)

 

.                                                        (4)

 

В (2)  есть суммарный заряд свободных электронов во внешней оболочке ШМ, величина  задаёт период вращения электронов, так что ток  в соответствии со своим определением получается как отношение всего движущегося заряда ко времени, равном периоду вращения электронов. Соотношение (3) описывает магнитное поле  на оси кольцевого тока , с радиусом кольца, равным ,  есть магнитная проницаемость среды внутри ШМ,  обозначает магнитную постоянную.

В (4) представлено условие равновесия электрона при его вращении в электронной оболочке ШМ, при этом  есть полный заряд ШМ,  есть количество положительно заряженных ионов внутри ШМ,  есть масса электрона,  есть относительная диэлектрическая проницаемость среды внутри ШМ,  есть электрическая постоянная.

Чтобы использовать условие равновесия сил для ионов (1), следует оценить среднюю массу  типичного иона воздуха и скорость  его движения, по порядку величины равную скорости теплового движения. Соотношение между кинетической и тепловой энергиями для иона имеет вид

 

,                                                          (5)

 

где есть постоянная Больцмана.

 

Из (1) и (5) следует приблизительное соотношение для магнитного поля в центре ШМ:

 

.                                                          (6)

 

При температуре воздуха внутри ШМ порядка  K  и при средней массе иона  кг как у молекулы азота, скорость ионов в (5) будет равна  м/с. Учитывая, что в данной ШМ  см,  см, из (6) и (3) при  находим магнитную индукцию внутри рассматриваемой ШМ, равную Тл, и суммарный ток электронной оболочки  А.

На основе рассмотренного подхода в [17] были найдены и другие параметры: ШМ в зависимости от её радиуса. Так, для ШМ с радиусом 7 см оценка количества  электронов во внешней оболочке и количество ионов  внутри ШМ даёт ; полный электрический заряд ШМ  Кл; скорость движения электронов во внешней оболочке  м/с; кинетическая энергия электронов  Дж; энергия магнитного поля 0,4 Дж; электростатическая энергия в объёме ШМ равна 2,8 Дж; внутренняя энергия ионизированного воздуха внутри ШМ 500 Дж; напряжённость электрического поля и электрический потенциал возле поверхности ШМ равны 530 кВ/м и 37 кВ, соответственно.

Давление от электрического расталкивания ионов внутри такой ШМ получается равным  Па, а магнитное давление, действующее на ионы, равно

 

 Па.                                             (7)

 

Магнитное давление  и давление  от электрического расталкивания ионов внутри ШМ не превышает атмосферного давления, так что внешняя оболочка с электронами, находящаяся под внешним атмосферным давлением, может удерживать ионизованный и заряженный воздух внутри ШМ.

Рассмотрим вращение электронов во внешней оболочке вблизи экватора ШМ с радиусом 7 см. На электроны здесь действует центростремительная сила в виде электрического притяжения от положительных ионов внутри ШМ. Если учитывать только эту силу, то выполняется теорема вириала в её простейшем виде, когда сумма удвоенной кинетической энергии электронов и их потенциальной энергии в электрическом поле равна нулю. Однако уравнение движения электронов в соответствии с условием равновесия плазмы в магнитной гидродинамике включает в себя ещё две небольшие по величине силы, одна из которых пропорциональна градиенту давления в электронной оболочке, а другая есть магнитная сила Лоренца [21]. Сила Лоренца может быть преобразована в член, содержащий градиент, а также в член, которым в первом приближении можно пренебречь. Так появляется соотношение , где  есть магнитное давление в оболочке с электронами,  есть давление электронов поперёк магнитных линий. Движущиеся во внешней оболочке со скоростью  электроны создают давление, по порядку величины равное

 

,                                                     (8)

 

где  Дж есть кинетическая энергия одного электрона,  есть кинетическая температура электронов,  есть масса электрона, при этом энергия  равна 22 кэВ в энергетических единицах. Если предположить, что , то с учётом (7-8) получается толщина оболочки ШМ, равная  см.

В случае образования ШМ в канале линейной молнии распределение электронов по скоростям может быть таким, что у электронов скорость  будет не только во внешней оболочке, но и в центральной части ШМ. В этом случае такие электроны будут вращаться в магнитном поле  и удерживаться в центре ШМ. Из равенства центростремительной силы и силы Лоренца следуют соотношения

 

,                           см.                              (9)

 

Радиус   в (9) ограничивает центральную часть ШМ, насыщенную быстро движущимися электронами. Эти электроны могут обеспечить то фиолетовое свечение в центре ШМ, которое наблюдалось в [26-27]. Сравнивая объём центральной части ШМ с радиусом  и объём внешней оболочки с толщиной , можно заключить, что плотность энергии электронов вблизи центра ШМ может на порядок превышать плотность энергии электронов внешней оболочки ШМ. Это позволяет объяснить тот факт, что при прохождении ШМ через стёкла обычно наблюдают отверстия диаметром от долей миллиметра и вплоть до размера самой ШМ [2], [28]. Иногда отверстия бывают оплавлены, иногда нет, в последнем случае можно предположить, что вначале стекло сильно нагревается, а затем выламывается под напором ШМ.

В Таблице 1 приведены расчётные параметры для ШМ различных размеров. Обозначения в таблице:  – радиус ШМ,  - общий электронный ток в оболочке ШМ,  - индукция магнитного поля в центре ШМ, – полная энергия с учётом энергий магнитного и электрического полей, энергии движения электронов и энергии плазмы внутри ШМ.

 

Таблица 1.

 

Параметры шаровых молний разных размеров

, см

, А

, Тл

, Кл

, Дж

1

20

2,2

7

503

17

0,5

10600

 

Радиус самых малых ШМ получается порядка 1 см, при этом энергию движения электронов и магнитную энергию можно считать приблизительно одинаковыми. При радиусе 7 см энергия ШМ получается равной 503 Дж, почти вся она заключена в тепловой энергии движущихся ионов и в потенциальной энергии ионизованных частиц.

Основная энергия мощной ШМ при её радиусе 17 см содержится в энергии ионизованных частиц и в энергии электромагнитного поля. При этом суммарная энергия величиной 10,6 кДж попадает в диапазон верхних значений наблюдаемого энергосодержания ШМ, определяемого через взаимодействие ШМ с окружающими предметами (оплавление металлических деталей, нагрев и испарение воды и т.д.).

 В рассматриваемой модели ШМ в целом должна быть заряжена положительно, чтобы ионы внутри ШМ могли долговременно удерживать электронную оболочку. Однако общий заряд  ШМ не может превышать такой величины, при которой напряжённость электрического поля на её поверхности превышает  кВ/м, во избежание пробоя атмосферного воздуха. Благодаря большой напряжённости электрического поля и быстрому вращению электронов в оболочке ШМ, возникают наблюдаемые эффекты шипения, потрескивания и испускания искр. Наблюдаемый радиус ШМ может больше, чем 17 см в Таблице 1, из-за свечения молекул ионизованного воздуха при их столкновениях с электронами и ионами. Кроме этого, в воздухе могут быть горящие частицы почвы, захваченные электрическим полем ШМ.

Как видно из Таблицы 1, максимальный электронный ток в ШМ достаточно близок к току в канале средней линейной молнии.

 

3. Электронно-ионная модель чёточной молнии

При построении модели чёточной молнии мы будем опираться на данные из [29]. С помощью покадровой реконструкции видеофильма, на котором была зафиксирована молния, бьющая в шпиль Останкинской телебашни в Москве 24 июля 2001 года, было обнаружено образование чёточной молнии на месте распада обычной молнии. Среднее расстояние между соседними чётками или бусинками чёточной молнии составило  м, средняя длина чётки   м, а ширина чётки при виде сбоку  м. Поскольку ширина канала первичной линейной молнии была 0,25 м, ширина чёток превышает ширину канала первичной молнии.

Мы можем считать, что каждая чётка имеет форму цилиндра с длиной  и диаметром , а площадь максимального бокового сечения такого цилиндра равна   м2. Поскольку скорость ветра на высоте шпиля 533 м в этот день равнялась  м/с, а динамическое давление напора воздуха выражается формулой  где  кг/м3 – плотность воздуха, то сила давления от ветра на каждую чётку имела следующую величину:

 

 Н.                                              (10)

 

Парадоксальность ситуации с данной чёточной молнией заключается в том, что несмотря на ураганный ветер, она за время своего существования в 0,625 секунды почти не сдвинулась с места. Видеозапись показала, что чётки молнии оставались на своих местах. Авторы [29] предположили, что чётки молнии, возможно, могли бы удерживаться электрическими силами, для этого случая они с учётом (10) подсчитали соответствующую напряжённость электрического поля :

 

,         ,          В/м,                  (11)

 

где  есть электрическая постоянная,  есть заряд одной чётки.

 

Напряжённость электрического поля  в (11) не превышает напряжённость пробоя воздуха  В/м.

Дело, однако, в том, что одними электрическими силами нельзя зафиксировать на своих местах свободные заряженные объекты – они будут неустойчивы и либо устремятся друг к другу, либо разлетятся в разные стороны, в зависимости от знаков зарядов.

Применим к анализу чёточной молнии данные о структуре шаровой молнии (ШМ), представленные в предыдущем разделе. Согласно электронно-ионной модели, ШМ имеет положительный заряд, а также магнитное поле, возникающее в основном от электронов, быстро вращающихся во внешней оболочке ШМ. Предположим, что строение отдельных чёток чёточной молнии такое же, как и у ШМ, тогда соседние чётки отталкиваются друг от друга электрическими силами, и одновременно притягиваются магнитными силами. В результате электромагнитные силы уравновешиваются, и чётки остаются на своих местах до полной потери энергии в молнии.

На Рисунке 3 показаны две соседние взаимодействующие между собой чётки. Собственная стабильность каждой чётки определяется тем, что внутренний объёмный положительный заряд удерживает электрическими силами вращающиеся электроны в оболочке чётки. При этом магнитное поле, возникающее от движения электронов, фиксирует внутри чётки положительные заряды при их вращении в данном магнитном поле.

 

 

 

Рассмотрим теперь устойчивость чёток друг относительно друга. Если у каждой чётки, как и у ШМ, имеется общий заряд , то сила электрического отталкивания одинаково заряженных чёток равна:

 

,                                                         (12)

 

где  – расстояние между соседними чётками.

 

Магнитную силу притяжения между чётками приблизительно рассчитаем, как силу взаимодействия двух одинаковых соленоидов, расположенных на одной оси на расстоянии  друг от друга:

 

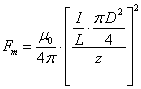.                                                   (13)

 

В (13) – ток электронов через цилиндрическую поверхность чётки, отношение  есть ток в расчёте на единицу длины чётки, величина  есть площадь поперечного сечения цилиндра чётки,   есть магнитная постоянная.

Если не учитывать действие остальных чёток, равновесие двух соседних чёток достигается при равенстве сил  (12) и  (13), что с учётом известного тождества   даёт:

 

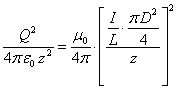,                 ,                      (14)

 

где – скорость света

 

Величину электронного тока  можно связать с количеством электронов  в цилиндрической оболочке чётки соответствующей формулой, так что при скорости электронов, стремящейся к скорости света, для тока аналогично (2) находим:

 

,                                                           (15)

 

где  есть элементарный электрический заряд.

 

То, что предельная скорость движения электронов в (15) может быть порядка скорости света, связано с экстремально большой силой тока в молнии, попавшей в шпиль Останкинской телебашни в Москве 24 июля 2001 года. При температуре в молнии порядка  K согласно [30], тепловая скорость электронов, вычисленная по формуле (4) с учётом массы электрона  вместо массы иона , даёт значение м/с.

 

С другой стороны, электрические силы могут разгонять электроны с большей эффективностью, чем тепловой нагрев газа. Это видно из того, что ступенчатый лидер при образовании молнии может двигаться со скоростью порядка 1/6 скорости света [20]. Таким образом формула (15) даёт оценку максимально возможного тока электронов . Более точные значения тока можно было бы определить, если учесть релятивистские поправки и условия протекания токов в ионизованной плазме и во внешней оболочке чёточной молнии.

Подстановка тока (15) в соотношение (14) даёт:

 

                                                           (16)

 

С другой стороны, общий заряд одной чётки  выражается как разность между всеми положительными и отрицательными зарядами, тогда с учётом (16) имеем:

 

,        ,      ,       (17)

 

так что количество  положительных ионов внутри чётки в 1,16 раз превышает количество  электронов в оболочке чётки.

Приравняем теперь силу напора ветра  из (10), действующую на чётку, к электрической силе  из (12), что даст возможность найти заряд чётки:

 

,             Кл.                 (18)

 

Подставляя заряд (18) в (16), определяем количество электронов в оболочке чётки:

 

,

 

а также количество некомпенсированных положительных ионов внутри чётки согласно выражению (17): .

Зная величину , можно оценить электронный ток в оболочке чётки из (15):

 

 А.                                               (19)

 

Индукция магнитного поля достигает максимума в центре чётки, и исходя из формулы для соленоида. равна:

 

 Тл.                                             (20)

 

Сравнение полученных значений внутренней индукции магнитного поля и электронного тока в оболочке чётки с соответствующими значениями для мощной ШМ из Таблицы 1 показывает, что они близки по величине. Исходя из величины магнитного поля, можно сделать вывод о том, что магнитное давление в центре чётки, определяемое по формуле ,

 

не превышает величины атмосферного давления, имеющегося в воздухе за пределами объёма чётки. Это означает, что вследствие магнитного давления объём чётки имеет возможность изменяться в некоторых пределах, подстраиваясь под действующие в чётке силы.

По всей видимости, образование чёточной молнии из обычной молнии происходит благодаря пинч-эффекту, при котором проводящий канал молнии в каком-либо месте пережимается магнитными силами, возникающими от протекающего тока. Действительно, по закону Ампера параллельные электронные токи в канале молнии притягиваются друг к другу. За счёт тока в молнии возникает магнитное поле, силовые линии которого имеют вид окружностей вокруг токового канала. Вследствие этого токовый канал молнии окружён оболочкой из электронов, вращающихся вдоль магнитных линий и экранирующих канал от внешней среды. Чем больше ток в молнии и больше магнитное поле, тем на меньшее расстояние от магнитных линий могут удаляться при своём движении электроны оболочки. В среднем это расстояние не превышает радиуса ларморовского вращения за счёт силы Лоренца.

При условии компенсации электрических сил за счёт одновременного присутствия положительных и отрицательных зарядов и при достаточной величине тока магнитное давление может превысить газодинамическое давление и привести к перестройке структуры молнии – поступательное движение зарядов вдоль всего канала молнии затрудняется и становится существенным вращательное движение в отдельных образованиях, то есть в чётках молнии. Условие возникновения пинч-эффекта описывается в данном случае соотношением Беннетта [31], в котором учитывается равенство плотностей магнитной энергии тока и тепловой энергии электронов и ионов газа:

 

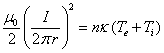.                                                (21)

 

Если подставить в (21) характерные значения параметров для линейной молнии согласно [30], а именно, радиус канала молнии  м, концентрация электронов  м–3 , электронная и ионная температуры  K, учесть значения магнитной постоянной  и постоянной Больцмана , то можно оценить величину тока:  А. Как и следовало ожидать, данный ток довольно большой и не меньше тока (19) в оболочке чётки. Сила тока в молнии, ударившей в шпиль Останкинской телебашни в Москве 24 июля 2001 года, действительно могла быть такой значительной, поскольку за счёт высоты телебашни уменьшается длина молнии и соответственно электрическое сопротивление её канала.

Дефрагментация линейной молнии на отдельные чётки начинается при уменьшении силы тока в канале молнии, за счёт чего уменьшается внешнее магнитное поле, а электронная оболочка отодвигается от канала. Так как движение электронов в оболочке молнии создаёт продольное магнитное поле в канале, то это поле, магнитное давление которого противодействует возникновению пинч-эффекта, также уменьшается. При расширении электронной оболочки молнии объём канала молнии в отдельных местах увеличивается до размеров чёток, при этом канал приобретает форму отдельных чёток с промежутками между ними, в основном как следствие электрического отталкивания положительно заряженного содержимого соседних чёток.

Как и в случае с шаровой молнией, свечение чёток может быть связано с трением взаимно перпендикулярных потоков ионов, один из которых направлен вдоль линий магнитного поля внутри чёток, а другой связан с вращением ионов вокруг этих магнитных линий.

Согласно [32], доля свободных электронов в воздухе близка к 0,7 при напряжённости электрического поля порядка 700 кВ/м. Внутри и за пределами чёток напряжённость поля может быть ещё больше, чем 1700 кВ/м согласно (11). Такие поля приводят к появлению большой доли свободных электронов, что даёт возможность обосновать количество  положительных ионов внутри чётки и количество  электронов в оболочке чётки в (17) в рамках электронно-ионной модели. С другой стороны, электрическое поле вблизи чёток имеет тот же порядок величины, что и критическое электрическое поле  кВ/м. Это приводит к быстрой потере энергии чёточной молнии за счёт разряда в окружающий воздух и к уменьшению на порядок времени жизни чёточных молний по сравнению со временем жизни шаровых молний. Дополнительным фактором, уменьшающим время жизни чёточных молний, является различие симметрии движения ионов и электронов внутри чёток и вблизи торцов цилиндрической поверхности чёток. Вследствие этого через торцы чёток происходит непрерывный отток горячего ионизованного воздуха в атмосферу, уменьшающий электрические заряды чёток и их энергию.

 

4. Обсуждение

4.1. Соответствие электронно-ионной модели с наблюдениями

Как указывалось в Разделе 2.1, ШМ могут возникать в изогнутых вторичных ветвях линейной молнии, когда в этих ветвях появляются достаточно большие круговые токи электронов. Такие токи генерируют дипольное магнитное поле, удерживающее положительные ионы внутри образующейся ШМ. В результате возникает стабильная конфигурация, показанная на рисунке 2. В этой конфигурации электронная оболочка содержит быстро движущиеся электроны, на которые действует электрическая сила со стороны положительно заряженных ионов внутри ШМ.

В качестве примера в [33] описывается случай, когда одна из ветвей линейной молнии, проходя почти горизонтально рядом с линией электропередачи, стала закручиваться по дуге и в этом месте сразу же возникла ШМ. В ряде других случаев ШМ возникала при пересечении друг с другом двух разных молний или их ветвей, а также в местах разветвления молнии.

Другой способ образования ШМ связан с пинч-эффектом, условие которого представлено в (21). В пользу такого способа говорит тот факт, что иногда обнаруживается не одна. а сразу две ШМ, соединённые друг с другом цепью светящихся бусин, подобно соединению чёток в чёточной молнии [30]. Изредка наблюдаются ШМ, имеющие форму удлинённого цилиндра [2]. В [33] наблюдался случай, в котором после удара линейной молнии из отрицательно заряженного облака канал молнии стал гаснуть, последовательно теряя своё свечение, начиная от облаков в сторону земли. Когда от светящегося канала осталась лишь малая часть вблизи земли, в этом месте возникла ШМ, которая, казалось, быстро вращается.

На основе подобных наблюдений делается вывод, что ШМ могут образовываться в канале разряда линейной молнии на стадии его распада через промежуточное состояние типа чёточной молнии. Кроме этого, ШМ могут возникнуть и во второстепенных ветвях линейной молнии, в которых может быть значительный электрический ток даже в отсутствие заметного свечения. Наблюдения из самолётов показывают, что множество ШМ возникает внутри грозовых облаков, что связана и с обилием ветвей каждой линейной молнии, и с большим количеством электрических разрядов внутри облаков и между облаками.

Таким образом ШМ может появиться даже в стороне от ярко сверкающего главного канала линейной молнии на любой высоте от земли. В некоторых случаях расстояние между возникающей ШМ и основным каналом линейной молнии может достигать сотен метров [34], что можно объяснить разветвлением основного канала молнии на несколько менее ярких каналов. Тогда ШМ возникает вблизи одного из вторичных каналов, и действительно, согласно наблюдениям многие ШМ возникают вблизи относительно слабых молний с током порядка десятков кА.

В [35] описываются случаи ещё больших расстояний между возникающими во время грозы ШМ и теми точками на земле, где были зафиксированы удары обычных линейных молний. Для объяснения такой ситуации следует учесть, что большие соседние грозовые облака могут иметь противоположный знак своего заряда. Так, одно облако может быть заряжено отрицательно в нижней части, и положительно в верхней части, а другое облако в целом может быть заряжено положительно ввиду существенного разряда своего отрицательного заряда, произошедшего ранее за счёт множества молний. Тогда первое облако будет создавать стандартную грозовую активность, включая молнии внутри самого облака (intra-cloud lightnings), ливень и обычные отрицательные молнии с движение электронов от облака к земле (negative cloud-ground lightnings). В отличие от этого, второе облако, движущееся в нескольких километрах от первого, скорее порождает положительные молнии с движение электронов от земли к облаку (positive cloud-ground lightnings) и ШМ на фоне слабого дождя. При этом вероятность возникновения ШМ при положительных молниях существенно превышает вероятность их возникновения при отрицательных молниях.

В [30] описаны случаи возникновения объектов сферической формы на конце линейной молнии, спускающейся с облака, но ещё не достигшей земли. Такие линейные молнии могут быть положительными молниями, в которых электроны движутся от земли к положительно заряженному облаку. Когда проводящий канал молнии достигает облака, первыми начинают своё движение в канале электроны вблизи облака. Их ток вызывает свечение канала молнии, которое распространяется вниз к земле. При этом электроны со стороны земли со всех сторон вливаются в канал как ручейки, образуя движущийся к земле светящийся сферический объект на конце молнии. Данный объект подпитывается энергией линейной молнии и может быть настолько мощным, что может полностью расщепить огромное дерево [33]. Существует вероятность того, что если облако успевает разрядиться раньше, чем светящийся канал коснётся земли, ток в молнии прекратится, и светящийся на конце молнии объект превратится в свободную ШМ. Мы можем предположить, что расчёты энергии очень мощных ШМ для 17 случаев наблюдения в [36] относятся именно к таким объектам.

Согласно [37-38], из 67 прямых наблюдений появления ШМ 31 событие произошло в непосредственной близости к каналу линейной молнии, 29 событий связано с «выдуванием» ШМ из металлических проводников типа электрических розеток, радиоприёмников, антенн и телефонных аппаратов, в остальных 7 случаях ШМ появлялась «ниоткуда» (from “nothing”). Достаточно часто ШМ возникает в закрытом помещении, при этом почти одновременно или в течение небольшого периода времени порядка минуты где-то совсем рядом раньше или позже происходит удар молнии [2], [30], [39]. Всё это указывает на то, что в помещении и рядом с ним под действием сильного электрического поля грозового облака формируются проводящие электричество ветви в ионизованном воздухе, готовые превратиться в канал будущей молнии. Чаще всего это должно происходить в тех помещениях, где нет высоких молниеотводов. Металлические проводники в помещении лучше переносят электричество, чем ионизованный воздух, поэтому чаще всего ШМ появляется возле этих проводников в момент электрического пробоя воздуха и следующего за этим импульса сильного электрического тока. Действительно, зафиксированы случаи, когда при замыкании или размыкании электрических цепей блоков аккумуляторов и мощных генераторов возникают большие токи и появляется ШМ [2], [30].

В [26-27] исследователь Дмитриев дал подробное описание наблюдаемой им ШМ диаметром около 14 см в горизонтальном направлении и с вертикальным размером до 16 см. Согласно этому описанию, внутренняя светящаяся оболочка (с яркостью, подобной яркости плазмы, нагретой в плазмотроне до температуры до 16000° ) была вытянута в вертикальном направлении, а все оболочки хорошо просматривались только в горизонтальном направлении. О вращении частиц в оболочках с дифференциальной скоростью говорили отдельные яркие конвективные струи. Центральная часть молнии была окружена областью толщиной 1-2 см с густым фиолетовым свечением, очень похожим на свечение воздуха при давлении 0,1 мм.рт.ст., бомбардируемого электронами с энергией в несколько десятков электронвольт. Следующая, наружная оболочка, толщиной около 2 см, также была неоднородна, напоминая по цвету тихий электрический разряд при атмосферном давлении или периферийное свечение электронного пучка с энергией в несколько десятков килоэлектронвольт, попадающего из вакуумной трубки в воздух при обычном давлении. Светло-голубое свечение этой части молнии быстро убывало с увеличением расстояния от центрального шара, постепенно сходя на нет. Наличие большой напряжённости электрического поля возле ШМ и энергичных частиц подтверждалось наблюдением их шипения, потрескивания и испускания искр как при электрическом разряде. Кроме этого, пробы воздуха, взятые после прохождения ШМ, показали повышенное содержание озона и окислов азота (приблизительно в 50-100 раз выше нормы). Требуемое соотношение концентраций озона и окислов азота можно получить при электрическом разряде в воздухе с напряженностью до 400 киловольт на 1 метр, а оценка необходимой электрической энергии в таком эквивалентном разряде за всё время жизни ШМ даёт значение 530 Дж.

В электронно-ионной модели становится понятным, почему в шаровой молнии Дмитриева все оболочки хорошо просматривались только в горизонтальном направлении. По всей видимости, в этой молнии ось вращения электронов во внешней оболочке и внутреннее магнитное поле были направлены вертикально, так что имелся поток ионов, движущихся вдоль магнитных силовых линий. Этот поток при взаимодействии с ионами, вращающимися в магнитном поле, и формировал наблюдаемые в горизонтальном направлении оболочки.

Представленные в Разделе 2.2 параметры достаточно хорошо описывают ШМ, которая наблюдалась в [26-27]. Существование сильного электрического тока в оболочке ШМ позволяет объяснить наблюдение, описанное в [33]. Во время грозы на контактах трансформатора воздушной телефонной линии образовалась ШМ, которая затем подлетела к коммутатору телефонной линии и разрядилась на его реле. Одновременно с этим ярко вспыхнули все 160 вызывных лампочек обоих коммутаторов, при том, что рабочее напряжение лампочек 24 вольта. По всей видимости, при разряде на контакты ШМ могла стать источником электродвижущей силы в сети, соединяющей лампочки. В другом примере ШМ разрядилась между телевизором и батареей отопления, при этом кинескоп телевизора вдруг засветился, хотя телевизор был выключен.

В [14], [40-41] анализировались почти полтысячи случаев наблюдения ШМ, в соответствии с которыми диаметр наиболее часто встречающейся ШМ находится в пределах 25-30 см. В то же время почти в 50 % случаев диаметр ШМ был меньше 25 см. Статистические зависимости, показывающие распределение нескольких тысяч наблюдений в зависимости от диаметра ШМ, можно найти в [42-44].

Согласно [45], параметр корреляции наблюдений диаметра ШМ в больших базах данных достигает величины 0,99. Описание наблюдений с помощью лог-нормального распределения даёт стандартное (среднеквадратическое) отклонение от среднего значения, равное 16 см для диаметра и 11 секунд для времени жизни ШМ При этом среднее значение диаметра ШМ для 4219 наблюдений равно  см. Наиболее вероятное значение энергии наблюдаемых ШМ лежит в пределах от 4,4 до 11 кДж. Указанные выше распределения хорошо согласуются с тем, что в электронно-ионной модели максимальный диаметр ШМ в Таблице 1 не превышает 34 см и может быть несколько больше с учётом светящегося гало. Энергия такой ШМ равна 10,6 кДж.

 

4.2. Соответствие электронно-ионной модели с теоретическими расчётами и с экспериментами

Возникновение ШМ в том месте, где линии тока имеют изгиб, подтверждается расчётом в [46] на основе взаимодействия тока в ветви линейной молнии с магнитным полем этого тока. Под действием электромагнитных сил загнутая ветвь ионизированного воздуха с током будет стремиться превратиться в кольцо, превращающееся затем в сферическую оболочку возникающей ШМ.

Начальная стадия образования ШМ в результате пинч-эффекта, использующая уравнения магнитогидродинамики [13], [21], описана в [5], [47].

Пробой воздуха в момент размыкания контактов с сильным током, или пробой воздуха вблизи контактов электрических цепей под действием высокого напряжения даёт излом в линии тока, подобный излому ветвей канала линейной молнии. Вблизи таких изломов за счёт резкого поворота линии тока появляется дополнительное магнитное поле, что является одним из условий возникновения ШМ. Это магнитное поле дипольного типа направлено перпендикулярно плоскости, в которой проходят линии тока или канала молнии, имеет собственную ось симметрии и тем самым отличается от магнитного поля прямого тока.

Благодаря такому магнитному полю положительные ионы, возникающие в месте пробоя за счёт ионизации током или напряжением, начинают вращаться вокруг оси симметрии поля, в то время как вокруг них быстро нарастает оболочка из электронов. Электроны движутся вдоль линий тока в скрещенных полях, одно из которых есть электрическое поле от ионов, а другое есть дипольное магнитное поле. В момент прекращения основного тока движение электронов вокруг области с положительными ионами за счёт удерживающей электрической силы продолжается, и формируется ШМ с замкнутым сферическим током электронов в её оболочке.

Одним из примеров математического описания образования ШМ в высоковольтном разряде вблизи двух контактов, один из которых есть катод, а другой есть анод электрической цепи, является статья [48]. В начальный момент разряда возникает стример, который может разветвиться как вблизи катода, так и вблизи анода. Далее стример приводит к образования плазмоида, который может превратиться в ШМ. В расчётах используется модель стримера, модифицированная с учётом диффузии электрического поля и ионов. С целью 3D моделирования процесса выбираются типичные единицы, задающие характерную длину (в виде длины свободного пробега электронов в азоте при нормальных условиях), масштабы времени, электрического поля, плотности и скорости электронов. Выводится дисперсионное соотношение, связывающее волновые числа, коэффициент диффузии электронов, напряжённость электрического поля и скорость стримера. Это позволяет построить графики распределения плотности электронов в стримере и в плазмоиде, распределения потенциала и электрического поля, и другие величины в зависимости от времени. Типичное время образования плазмоида размером 20 см составляет от 150 до 500 мс, при этом минимальная необходимая напряжённость электрического поля достигает величины 35-40 кВ/м [49]. Такого же порядка величины будут иметь электрические поля и в небольших ШМ в случае их возникновения вблизи электрических розеток, радиоприёмников, антенн и телефонных аппаратов, находящихся в закрытых комнатах и попавших под высокое напряжение от молнии.

В [50] было экспериментально показано, что создаваемые при разряде в лаборатории светящиеся низкотемпературные плазмоиды имеют тонкую оболочку, содержащую отрицательные заряды и предохраняющую смешивание содержимого плазмоидов с атмосферным воздухом. При соприкосновении плазмоидов с проводниками последние как правило оплавляются, а взаимодействие с диэлектриками существенно более слабое. Плазмоиды также реагируют на луч лазера, имеют некомпенсированный электрический заряд, при этом температура воздуха внутри таких искусственно созданных плазмоидов составляет величину порядка 200 С. Однако цветовая температура плазмоидов может достигать 2000 С, что говорит о нетепловой природе излучения.

В [51] было обнаружено, что во внешней оболочке плазмоидов имеется резкий градиент плотности массы. Согласно наблюдениям в [25], природная ШМ оказалась чувствительной к расположенной рядом с ней высоковольтной (35 кВ) линии электропередачи (high-voltage (35 kV) transmission lines), так как частота изменения интенсивности свечения ШМ совпала с частотой 50 Гц электрического тока в линии электропередачи. Хорошо известно также, что появление ШМ приводит к возникновению шумов во включённом радиоприёмнике.

Все эти факты можно объяснить следующим образом. В электронно-ионной модели положительные ионы внутри ШМ слабо притягиваются электронами из внешней оболочки, так как электрическое поле от этой оболочки внутри сферы близко к нулю из-за уравновешивания всех электрических сил ввиду симметрии сферы. Действительно, заряд, равномерно распределённый по поверхности пустотелой сферы, не создаёт внутри сферы электрическое поле, как это следует из теоремы Гаусса. Поэтому ионы могут достаточно свободно распределяться в объёме внутри ШМ, достигая состояния равновесного вращения во внутреннем магнитном поле, при этом рекомбинация ионов и электронов в ШМ существенно замедляется из-за пространственного разделения зарядов.

В первом приближении можно считать, что электроны во внешней оболочке образуют электронную жидкость, равномерно заполняющую всю оболочку и находящуюся в непрерывном вращении. Быстро движущиеся электроны создают сильный ток, способный оплавлять проводники, обжигать деревянные предметы, нагревать и испарять воду. Взаимодействие электронов с окружающим ШМ воздухом приводит к его ионизации и сопровождается радиоизлучением, воспринимаемым радиоприёмниками как шум. Будучи объектом с электрически связанными пространственно разделёнными положительными и отрицательными зарядами, ШМ реагирует на луч лазера, так как фотоны воздействуют на электроны во внешней оболочке. Наличие у ШМ заряда обеспечивает взаимодействие этого заряда с переменным электрическим полем вблизи линий электропередач, что выражается в изменении формы ШМ и яркости свечения ШМ с частотой тока в этих линиях.

Согласно [11] и в соответствии с [52-53], в лаборатории в скрещенных переменных электрическом и магнитном полях создавались плазменные ШМ с максимальным диаметром до 94 см. Такие ШМ, как показали измерения, имели пространственно разделённые объёмные электрические заряды разных знаков, с движением зарядов по окружностям, электрические токи этих зарядов и соответствующее магнитное поле дипольного типа. Распределение интенсивности излучения, в зависимости от текущего радиуса от центра ШМ, по своей форме близко к распределению интенсивности, наблюдаемой у природных ШМ. При этом максимум интенсивности достигается вблизи оболочки ШМ, за пределами которой имеется достаточно быстро затухающее светящееся гало. Поскольку пробники при контакте с плазменной ШМ заряжаются положительно, предполагается, что оболочка ШМ содержит релятивистские протоны, а в центре ШМ содержатся электроны.

В электронно-ионной модели ШМ фактически есть небольшой кусок линейной молнии, закрученный в клубок с характерным размером 10 - 40 сантиметров. Соответственно, в обоих типах молний токи и магнитные поля могут быть близки по величине. Поскольку ШМ в данной модели имеет общий положительный заряд, это может объяснить то, что в [11] плазменные ШМ заряжали положительно пробники электрического заряда. Однако в электронно-ионной модели в оболочке ШМ находятся не протоны, а электроны.

Подтверждение электронно-ионной модели ШМ можно найти в [54], где изучалась возможная форма магнитного поля ШМ, которая могла бы обеспечить движение ШМ вдоль провисших проводников, включая лини электропередач. Учитывая свойства движения ШМ в вязком воздушном потоке, делается вывод, что электростатическое поле заряженной положительно ШМ должно быть центрально-симметричным. Магнитное поле ШМ должно иметь ось симметрии, а токи, создающие это магнитное поле, должны быть азимутальными. Используемое в расчётах уравнение движения ШМ вдоль провода учитывает напор ветра и взаимодействие магнитного поля ШМ с электрическим током в проводе, возникающим за счёт утечки заряда с поверхности ШМ в провод. Показывается, что такое движение вдоль провода возможно лишь в случае, когда токи, генерирующие магнитное поле ШМ, сосредоточены в её поверхностном слое. Действительно, токи в объёме ШМ будут взаимодействовать с магнитным полем так, что ШМ должна всё время увеличивать свой объём, что не наблюдается. Для конфигурации с поверхностным током находятся выражения компонент векторного потенциала и магнитного поля ШМ в сферических координатах.

В [55-56] была рассмотрена гидродинамическая модель ШМ с целью описания её движения через небольшие отверстия. При движении за пределами отверстия использовались уравнения движения недеформированного жидкого шара в потоке идеальной жидкости точечного гидродинамического источника, записанные в сферических координатах. Эти уравнения модифицируются в уравнение Эйлера с учётом уравнения непрерывности для описания движения ШМ в отверстии, диаметр которого на порядок меньше диаметра ШМ, что приводит к превращению формы ШМ в струю. Решения уравнений находились путём численного моделирования при разумных предположениях о времени прохождения через отверстие и о поведении ШМ в воздушном потоке. Одним из выводов является то, что оболочка ШМ должна иметь нулевую вязкость по отношению к окружающей среде, а вещество ШМ представляет собой идеальную несжимаемую жидкость.

В [57] проводились эксперименты с заряженными мыльными пузырями диаметром 3 см, несущими электрический заряд от 10 до 15 нКл. При таком заряде мыльные пузыри имеют тенденцию притягиваться индуцированными зарядами к ближайшему заземленному проводнику. Согласно выводам в [57], это ставит под сомнение возможность движения заряженных ШМ в горизонтальном направлении и вблизи заземлённых проводников, если заряд ШМ достаточно велик.

Что можно сказать тогда в отношении возможности горизонтального движения ШМ, описанной в [26-27], которая имела радиус 7 см ? Если исходить из электронно-ионной модели, электрический заряд такой ШМ равен  Кл. Согласно расчётам в [17], на ШМ действует подъёмная сила Архимеда от горячего воздуха внутри ШМ, а также электрическая сила, действующая между зарядом ШМ и наведёнными зарядами на земле. Равенство этих сил осуществляется при высоте ШМ над землёй порядка 10 см, в этом случае ШМ может оказаться привязанной к какому-либо предмету на земле. Если же ШМ имеет радиус 17 см и соответствующий заряд  Кл, то равновесное состояние будет осуществляться при высоте 90 см.

С течением времени заряд ШМ может изменяться из-за взаимодействия с окружением или при частичном распаде, приводя к изменению равновесного состояния. По мере остывания воздуха в ШМ уменьшается её объём, а при потере электронов с наружной оболочки может увеличиваться и заряд Q. Поэтому ШМ может всплыть над землёй и далее плавно перемещаться в зависимости от рельефа местности, ветра и электрических полей от грозовых облаков. Достаточно часто при переходе от прикреплённой ШМ к свободной она взмывает вверх, а затем по наклонной линии уходит к облакам. Последнее можно объяснить сильным электрическим полем, действующим на положительный заряд ШМ со стороны отрицательно заряженной нижней части облака. Из равенства силы Архимеда и электрической силы можно оценить минимальную напряжённость электрического поля, которая может влиять на движение ШМ:

 

.                                                         (22)

 

Для ШМ с радиусом 7 см и зарядом  Кл электрическое поле получается равным  В/м. Для сравнения, напряжённость поля в грозовую погоду вполне может достичь величины  В/м и более, если исходить из разности потенциалов между облаками и землёй, достигающей  В.

Сопоставление заряженных мыльных пузырей и ШМ не вполне корректно потому, что в этих пузырях нет очень горячего воздуха и соответствующей силы Архимеда. Кроме этого, следует рассмотреть взаимодействие электрического заряда пузыря и массивного проводника на земле более подробно. Для того, чтобы пузырь мог притягиваться к проводнику, электрический заряд пузыря своим электрическим полем должен разделить заряды в проводнике. Для этого требуется выполнить некоторую работу, которая в данном случае возможна за счёт силы тяжести, действующей на пузырь. Чем ближе оказывается пузырь к проводнику, тем больше в проводнике разделяются заряды и сильнее будет притяжение пузыря к проводнику.

В отсутствие силы Архимеда баланс сил таков, что пузыри будут притягиваться к проводникам на земле, пока не столкнутся с ними. В отличие от этого, движение ШМ управляется не только силой тяжести, но и силой Архимеда, а также электрическими силами от зарядов на земле и на облаках и давлением ветра. Ввиду этого движение ШМ может быть многообразнее, включая в себя любые движения по горизонтали и вертикали.

В качестве иллюстрации можно привести случай с двумя исследователями согласно [33], в котором во время грозы в горах на высоте 2700 м возникло настолько сильное электрическое поле, что волосы наэлектризовались и встали дыбом. При ударе молнии на расстоянии 25 м от наблюдателей в месте попадания молнии в землю стал закручиваться и расти клубок, превратившийся в ШМ. Затем ШМ подпрыгнула на 35 см над землёй и поплыла в сторону. Когда ШМ цеплялась за камни, летели искры и раздавался звук, похожий на металлический звон и стук детской погремушки одновременно. В других подобных случаях ШМ остаются недалеко от земли либо двигаются на небольшой высоте.

В [58] весьма оригинальным способом был определён электрический заряд и потенциал поля вблизи поверхности ШМ. Для этого был использован тот факт, что ШМ в соответствии с показаниями очевидца двигалась по искривлённой линии приблизительно на высоте 1,5 м над поверхностью реки вдоль плотов из брёвен с начальным углом 30° к ветру. При описании одномерного движения ШМ в уравнении Навье-Стокса были приняты в учёт давление ветра, зависящее от высоты, и электростатическое притяжение, находимое с помощью метода изображений, причём плоты из брёвен рассматривались как диэлектрический выступ над водой. В результате при радиусе ШМ 10 см заряд ШМ получился равным  Кл, а электрический потенциал 42 кВ.

Согласно [59], ШМ с радиусом 15 см имеет заряд порядка нескольких микрокулон и плотность электрической энергии порядка одной сотой джоуля на кубический сантиметр.

Параметры ШМ в [58-59] вполне согласуются с нашими расчётами параметров ШМ в электронно-ионной модели в Разделе 2.2 и в Таблице 1. Кроме этого, согласно расчётам в [17], электрическая энергия ШМ с радиусом 17 см при общем заряде ШМ  Кл равна 1,3 кДж. Если разделить эту энергию на объём ШМ, получится плотность электрической энергии порядка 0,06 Дж/см3 , что соответствует значению плотности электрической энергии в [59].

 

4.3. Дополнительные замечания

Новизна электронно-ионной модели по сравнению с протон-электронной моделью в [10-11] заключается в том, что во внешней оболочке ШМ находятся не протоны, а релятивистские электроны, токи которых генерируют сильное магнитное поле. Это магнитное поле фиксирует положительные ионы воздуха внутри ШМ и заставляет их вращаться вокруг линий магнитного поля. В свою очередь, внутренний электрический заряд ШМ удерживает электроны при их вращении в оболочке ШМ. Тем самым обеспечивается долговременная стабильность ШМ, заряженной в целом положительно. Разделение зарядов в ШМ происходит на стадии её образования , при этом ключевую роль играет дипольное магнитное поле в искривлённом канале в ветви линейной молнии. При сильном токе в линейной молнии важным становится пинч-эффект.

Найденные в Разделе 2.2 параметры ШМ, зависящие от радиуса ШМ, подтверждаются наблюдениями, описанными в Разделе 4.1, а также теоретическими расчётами и экспериментами, представленными в Разделе 4.2.

Одним из преимуществ электронно-ионной модели является то, что с её помощью нам удалось объяснить не только структуру ШМ, но и структуру чёточной молнии, а также изредка наблюдаемых конструкций из двух связанных ШМ. В отличие от одиночной ШМ сфероидальной формы, в чёточной молнии имеется несколько чёток почти сферической или цилиндрической формы, связанных между собой электрическими силами отталкивания и магнитными силами притяжения. Указанные силы совместно с атмосферным давлением и давлением горячей плазмы формируют размеры возникающих чёток, во многих случаях превышающие диаметр канала первичной линейной молнии.

Согласно [1-2], чётки часто имеют форму, близкую к сферической. Мы можем связать это с действием магнитного давления, возникающего за счёт вращения электронов в оболочке каждой чётки и порождающего сильное магнитное поле внутри чёток. В соответствии с наблюдениями, чем больше электронные токи и магнитное поле в чётках, тем больше размеры чёток и запасённая в них энергия, и тем медленнее перестают светиться такие чётки.

Чётки возникают в канале обычной линейной молнии и потому теряют энергию за счёт сквозных токов в ещё проводящем электричество горячем воздухе канала молнии. Нагретый воздух внутри чётки изолируется электронной оболочкой со стороны боковой поверхности, но может выходить с торцов чётки в канал молнии. Из наблюдений следует, что чётки могут быть видны до 2,5 секунд. Как показывают представленные в Разделе 3 расчёты, электромагнитные силы, удерживающие чётки, настолько велики, что чётки могут выдерживать даже давление ураганного ветра.

Электронно-ионная модель может быть полезна для анализа и объяснения результатов экспериментов [60], в которых при электрическом разряде в водной среде наблюдались светящиеся объекты в виде шаров с размерами порядка нескольких миллиметров. При разряде происходит диссоциация воды на ионы водорода и кислорода, которые попадают внутрь этих шаров, с последующим горением водорода. То, что близко расположенные шары сливаются друг с другом, может быть связано с тем, что магнитная сила притяжения (13) при малых расстояниях между шарами будет существенно больше, чем сила электрического отталкивания (12). При столкновении шаров с препятствием они взрывались, что можно объяснить остановкой заряженных частиц, быстродвижущихся в оболочках шаров, с последующей рекомбинацией ионов и соответствующим быстрым выделением энергии.

Заметим, что в микроуровне также могут существовать объекты, подобные по своим свойствам ШМ и чёточной молнии. Так, в [61-62] можно найти обзор свойств так называемых Exotic Vacuum Objects (EVO), представляющих собой отрицательно заряженные кластеры (charge clusters) сферической формы размером от 1 до 20 мкм. Соотношение количества электронов и ионов в EVO достигает . EVO создавались в микродуговом разряде при малом напряжении и небольшой мощности (low voltage/low power micro-arc discharge). имели скорости до 1/10 скорости света и существовали до  с. Удивительным свойством EVO является их способность создавать такие же цепочки, как и в чёточной молнии. Как и ШМ, EVO могут взрываться, излучая при этом в рентгеновском диапазоне. При встрече с препятствиями EVO проделывают в них глубокие тоннели. Для объяснения этого свойства в [63] EVO рассматриваются как объекты в системах импульсного осаждения и как кумулятивные заряды (pulsed deposition systems and shaped-charge munition). Среди ряда вопросов, ожидающих решения в рамках аналогии ШМ и EVO, можно выделить следующие: Какие силы заставляют EVO формировать и поддерживать сферическую форму, несмотря на существенное преобладание количеств электронов над ионами и отталкивание электронов друг от друга? Каким образом EVO могут объединяться в цепочки, если учесть их сильное электростатическое отталкивание друг от друга?

 

5. Заключение

К основным результатам данной работы относится вычисление параметров ШМ в Разделе 2,2 и параметров чёточной молнии в Разделе 3. В рамках электронно-ионной модели показывается идентичность конфигурации токов и структуры расположения объёмных электрических зарядов в ШМ и в чётках чёточной молнии. Как и ШМ, каждая чётка несёт на себе электрический заряд и генерирует магнитное поле. В результате соседние чётки в чёточной молнии удерживаются двумя силами, одна из которых есть магнитная сила притяжения чёток, а другая есть электрическая сила отталкивания одноимённо заряженных чёток.

Представленные в Разделе 2,2 и в Разделе 3 формулы описывают ШМ и чёточную молнию в статическом квазистабильном состоянии. Эти формулы  позволяют объяснить долговременную устойчивость обеих молний по сравнению с очень малым временем свободного существования изначально покоящихся и разделённых объёмных электрических зарядов в ионизованной  плазме. Действительно, электрическая сила между объёмными зарядами в плазме настолько велика, что ей может противостоять только магнитная сила, возникающая за счёт быстрого движения зарядов. В электронно-ионной модели основное магнитное поле ШМ и чёток чёточной молнии генерируется током электронов в оболочке ШМ и чёток, соответственно. Такое движение электронов является следствием эволюции токов электронов в загнутых ветвях или в канале линейной молнии, а также следствием эволюции стримеров в искусственно создаваемых электрических разрядах. В результате возникает дипольное магнитное поле пространственно загнутого тока, которое может трансформироваться в дипольное магнитное поле ШМ и чёток.

Положительно заряженные ионы воздуха, удерживаемые магнитной силой Лоренца, притягивают к себе электроны в оболочке. Благодаря сферической симметрии ШМ и цилиндрической симметрии чёток, силы электрического отталкивания ионов друг от друга и силы электрического отталкивания электронов друг от друга уравновешиваются электрическим притяжением ионов и электронов, с учётом центростремительной силы от вращения электронов и небольшой разницы давлений воздуха внутри и снаружи ШМ. Таким образом, устойчивость ШМ и чёточной молнии достигается в основном за счёт электромагнитных сил.

Динамические аспекты, связанные с фазами образования и исчезновения ШМ и чёточной молнии в рамках электронно-ионной модели, включая рекомбинацию зарядов и эффекты ионизации (charge recombination and ionizing effects), описаны в данной работе кратко, поскольку требуют отдельной статьи с привлечением всего аппарата физики ионизованной плазмы.

 

Список использованных источников

1.        Minin V.F. and Baibulatov F.Kh. On the nature of beaded lightning. Dokl. Akad. Nauk SSSR, Vol. 188 (4), pp. 795-798 (1969).

2.        Barry J. Ball Lightning and Bead Lightning, Springer, Boston, MA, (1980), http://dx.doi.org/10.1007/978-1-4757-1710-5, ISBN 978-1-4757-1710-5.

3.        Morrow R. The origin of ball and bead lightning from an expanded lightning channel. Journal of Atmospheric and Solar-Terrestrial Physics, Vol 195, 105116 (2019). https://doi.org/10.1016/j.jastp.2019.105116.

4.        Morrow R. A new comprehensive theory for ball and bead lightning. Australian Physics, Vol. 57, Issue 4, pp. 14-20 (2020).

5.        Wooding E.R. Ball Lightning. Nature, Vol. 199. N4890, pp. 272-273 (1963). https://doi.org/10.1038/199272a0.

6.        Johnson P.O. Ball Lightning and Self-containing Electromagnetic Fields. American Journal of Physics, Vol. 33, No 2, pp. 119-123 (1965). https://doi.org/10.1119/1.1971261.

7.        Tsui K.H. Ball lightning as a magnetostatic spherical force-free field plasmoid.  Physics of Plasmas, Vol. 10, pp. 4112-4117 (2003). https://doi.org/10.1063/1.1605949.

8.        Shafranov V.D. On Magnetohydrodynamical Equilibrium Configurations. Soviet Journal of Experimental and Theoretical Physics, Vol. 6, No 3, pp. 545-554 (1958). // Шафранов В.Д. О равновесных магнитогидродинамических конфигурациях. ЖЭТФ, Т. 33, Вып. 3. С. 710-722 (1957).

9.        Wu H. and Chen Y. Magnetohydrodynamic equilibrium of plasma ball lightning. Physics of Fluids B, Vol. 1 (8), pp. 1753-1755 (1989). https://doi.org/10.1063/1.858903.

10.    Oreshko A.G., Oreshko A.A. and Mavlyudov T.B. Proton-electron model of ball lightning structure. Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 182, pp. 194-199 (2019). https://doi.org/10.1016/j.jastp.2018.11.017.

11.    Oreshko A.G. On physical investigation of ball lightnings. Journal of Plasma Physics, Vol. 87(6), 905870609 (2021). https://doi.org/10.1017/S0022377821000933 .

12.    Shmatov M. Ball lightning with the nonrelativistic electrons of the core. Journal of Plasma Physics, 81(4), 905810406 (2015). https://doi.org/10.1017/S0022377815000410.

13.    Ludwig G.O. and Saba M.M.F. Bead lightning formation. Physics of Plasmas, Vol. 12, 093509 (2005). https://doi.org/10.1063/1.2048907.

14.    Keul A.G. A brief history of ball lightning observations by scientists and trained professionals. Hist. Geo Space Sci., Vol. 12, pp. 43–56 (2021). https://doi.org/10.5194/hgss-12-43-2021.

15.    Fedosin S.G., Kim A.S. Kriterii Analiza Modelei Sharovykh Molnii (Criteria of Analysis of Ball Lightnings Models), Moscow: VINITI (All Union Inst. of Scientific and Technical Info.), record N 3071-В00 of 06.12.2000, 31 pages. In Russian. Федосин С.Г., Ким А.С. Критерии анализа моделей шаровых молний. Деп. в ВИНИТИ, рег. №. 3071-В00 от 06.12.2000, 31 с.

16.    Fedosin S.G. and Kim A.S. Electron-Ionic Model of Ball Lightening. Journal of new energy, Vol. 6, No. 1, pp. 11-18 (2001). http://dx.doi.org/10.5281/zenodo.891156.

17.    Fedosin S.G. and Kim A.S. The Physical Theory of Ball Lightning. Applied physics (Russian Journal), No. 1, pp. 69-87 (2001), in Russian. https://applphys.orion-ir.ru/appl-01/01-1/01-1-e.htm . Федосин С.Г., Ким А.С. Физическая теория шаровой молнии. Прикладная физика, N 1. С. 69–87 (2001).

18.    Ким А.С., Федосин С.Г. Способ получения шаровой молнии // Патент РФ № 2210195, МПК 7H05H1/00, G09B23/18, Бюлл. № 22, 2003. In Russian. https://searchplatform.rospatent.gov.ru/media/National/RU/C2/2003/08/10/0002210195//MAIN.PDF.

19.    Fedosin S.G. Sovremennye problemy fiziki : v poiskakh novykh printsipov, 192 pages., URSS, Moskva, 2002. ISBN 5-8360-0435-8. (The Problems of Modern Physics. Searching for New Principles, http://lccn.loc.gov/2009457352 ). In Russian. Федосин С.Г. Современные проблемы физики. В поисках новых принципов. М.: Эдиториал УРСС, 2002, 192 с.

20.    Feynman R.P., Leighton R.B., Sands M. The Feynman lectures on physics. Vol. 2, Addison-Wesley, Reading, Massachusetts (1964).

21.    Fridman A. and Kennedy L.A. Plasma Physics and Engineering, 2nd ed. CRC Press, p. 20 (2011), 873 pages. ISBN 978-1-4398-1229-7.

22.    Zhang W., Fisher T.S. and Garimella S.V. Simulation of Ion Generation and Breakdown in Atmospheric Air. CTRC Research Publications. Paper 292 (2004). http://dx.doi.org/10.1063/1.1806264.

23.    Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003. // Четырёхмерное уравнение движения вязкого сжимаемого заряженного вещества с учётом поля ускорений, поля давления и поля диссипации.

24.    Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в теории релятивистских векторных полей.

25.    Cen J., Yuan P. and Xue, S. Observation of the optical and spectral characteristics of ball lightning, Phys. Rev. Lett., Vol. 112, 035001 (2014), https://doi.org/10.1103/PhysRevLett.112.035001.

26.    Dmitriev M.T. Priroda Sharovoi Molnii (The Nature of Ball Lightning), Priroda (Nature), No 6, pp. 98-106 (1967). In Russian. Дмитриев М.Т. Природа шаровой молнии // Природа. 1967. N 6. С.98-106.

27.    Dmitriev М.I. Chemical Analysis of Ball Lightning. Foreign Science Bull., Vol. 3, No. .9, p. 30 (1967).

28.    Bychkov V.L., Nikitin A.I., Ivanenko I.P., Nikitina T.F., Velichko A.M. and Nosikov I.A. Ball lightning passage through a glass without breaking it. Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 150-151, pp. 69-76 (2016). http://dx.doi.org/10.1016/j.jastp.2016.10.018.

29.    Марахтанов М., Марахтанов А. Молния на ураганном ветру // Наука и жизнь, 2002, № 6, С. 14.

30.    Singer S. The Nature of Ball Lightning. New York, Plenum Press, 239 p. (1971). Сингер C. Природа  шаровой  молнии. – М.: Мир, 1973, 239 с.

31.    Bennett W.H. Magnetically Self-Focussing Streams. Phys. Rev. Vol. 45 (12), pp. 890–897 (1934). http://dx.doi.org/10.1103/physrev.45.890.

32.    Boissonnat G., Fontbonne J.-M., Colin J., Remadi A. and Salvador S. Measurement of ion and electron drift velocity and electronic attachment in air for ionization chambers. arXiv, Sep. 13, 2016. doi: 10.48550/arXiv.1609.03740.

33.    Grigoriev A.I. Ball Lightning. Yarosl. state univ. named after P.G. Demidov. Yaroslavl, YarSU (2006). 200 pages. ISBN 978-5-8397-0512-8. In Russian. // Григорьев А.И. Шаровая молния. Яросл. гос. ун-т. им. П.Г. Демидова. Ярославль, ЯрГУ (2006). 200 с. ISBN 978-5-8397-0512-8. http://www.lib.uniyar.ac.ru/edocs/iuni/20060703.pdf.

34.    Stephan K.D., Sonnenfeld R., Keul A.G. First comparisons of ball-lightning report website data with lightning-location-network data. Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 240, 105953 (2022). https://doi.org/10.1016/j.jastp.2022.105953.

35.    Boerner H. Ball Lightning: A Popular Guide to a Longstanding Mystery in Atmospheric Electricity. Springer, p. 110 (2019), 367 pages, ISBN 9783030207830.

36.    Bychkov A.V., Bychkov V.L., Abrahamson J. On the energy characteristics of ball lightning. Philosophical Transactions A, Math Phys Eng Sci., Vol. 360(1790), pp. 97-106 (2002). https://doi.org/10.1098/rsta.2001.0922.

37.    Stakhanov I.P. The Physical Nature of Ball Lightning. Atomizdat, Moscow (1979). In Russian.

38.    Smirnov B.M. The Properties and the Nature of Ball Lighting. Physics Reports, (Review Section of Physical Letters), Vol. 152, No. 4, pp. 177-226 (1987). https://doi.org/10.1016/0370-1573(87)90142-6.

39.    Stakhanov I.P. About the Physical Nature of Ball Lightning. Energoatomizdat, Moscow (1985). In Russian.

40.    Keul A.G. and Stummer O. Comparative analysis of 405 Central European ball lightning cases. Journal of Meteorology, Vol. 27, pp. 385-393 (2002), http://www.ijmet.org/wp-content/uploads/2016/09/274.pdf.

41.    Keul A.G. The Ball Lightning Controversy: Empirical Case Studies. In: Pfeifer, K., Pfeifer, N. (eds) Forces of Nature and Cultural Responses. Springer, Dordrecht (2013). https://doi.org/10.1007/978-94-007-5000-5_3.

42.    Stenhoff M. Ball Lightning. An Unsolved Problem in Atmospheric Physics. New York, Kluwer Academic, Plenum Publishers. (1999). ISBN 0-306-46150-1.

43.    Amirov A.K. and Bychkov V.L. A study of the distribution function of the parameters of ball lightning. Journal of Meteorology, Vol. 20(199), pp. 159-164 (1995).

44.    Smirnov B.M. Observational parameters of ball lightning. Physica Scripta, Vol. 48, Number 5, pp. 638 (1993). https://doi.org/10.1088/0031-8949/48/5/023.

45.    Smirnov В.М. Observational properties of ball lightning. Soviet Physics Uspekhi, Vol. 35 (8), pp. 650-670 (1992). https://doi.org/10.1070/PU1992v035n08ABEH002254.

46.    Li Zicheng and Yang Guohua. Research on the Formation Mechanism and Characteristics of Ball Lightning. XV International Conference on Atmospheric Electricity, 15-20 June 2014, Norman, Oklahoma, U.S.A. https://www.nssl.noaa.gov/users/mansell/icae2014/preprints/Li_150.pdf.

47.    Morrow R. A new theory for the expansion of lightning channels from a diameter of centimetres to metres via ionizing waves. Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 189, pp. 18-26 (2019). https://doi.org/10.1016/j.jastp.2019.04.003.

48.    Trunev A.P. Simulation of Ball Lightning in conducting Enviroment. Polythematic Online Scientific Journal of Kuban State Agrarian University, Vol. 130 (06), pp. 1-31 (2017). In Russian. https://doi.org/10.21515/1990-4665-130-027. // Трунев А.П. Моделирование шаровой молнии в проводящей среде. Научный журнал КубГАУ, № 130 (06), c. 1-31 (2017). http://ej.kubagro.ru/2017/06/pdf/27.pdf.

49.    Fantz U., Kalafat S., Friedl R., Briefi S. Generation of an atmospheric plasmoid from a water discharge: An analysis of the dissipated energy. Journal of Applied Physics, Vol. 114 (4), 043302 (2013). https://doi.org/10.1063/1.4816311.

50.    Shabanov G.D. On the possibility of making a natural ball lightning using a new pulse discharge type in the laboratory. Physics-Uspekhi, Vol. 62 (1), pp. 92-107 (2019). https://doi.org/10.3367/UFNe.2018.03.038318.

51.    Friday D.M., Broughton P.B., Lee T.A., Schutz G.A., Betz J.N, and Lindsay C.M. Further Insight into the Nature of Ball-Lightning-Like Atmospheric Pressure Plasmoids. J. Phys. Chem. A, Vol 117 (39), pp. 9931–9940 (2013). https://doi.org/10.1021/jp400001y.

52.    Oreshko A.G. Research of a ball lightning and prospects of its use for applied purposes. In VI International Conference on Plasma Physics and Plasma Technology. Contributed Papers, Minsk, Vol. 1, pp. 137-140 (2009).

53.    Oreshko A.G. An investigation of the generation and properties of laboratory produced ball lightning. Journal of Plasma Physics, Vol. 81(3), 905810321 (2015). https://doi.org/10.1017/S0022377815000197.

54.    Gaidukov N.I. Equations of motion of ball lightning in the magnetic field of a hanging conductor. Zhurnal Tekhnicheskoi Fiziki, Vol. 63, No. 10, pp. 20-29 (1993). In Russian. // Гайдуков Н.И. Уравнения движения шаровой молнии в магнитном поле провисшего проводника. Журнал технической физики, Том 63, Выпуск 10, с. 20-29 (1993). http://journals.ioffe.ru/articles/viewPDF/15748.

55.    Gaidukov N.I. A hydrodynamic model of ball lightning leakage through a narrow opening in a plane screen. Zhurnal Tekhnicheskoi Fiziki, Vol. 61, No. 11, pp. 49-56 (1991). In Russian. // Гайдуков Н.И. Гидродинамическая модель процесса протекания шаровой молнии через узкое отверстие плоского экрана. Журнал технической физики, Том 61, Выпуск 11, с. 49-56 (1991). http://journals.ioffe.ru/articles/viewPDF/24805.

56.    Gaidukov N.I. A hydrodynamic model of motion of ball lightning jet through a narrow opening in a plane screen. Zhurnal Tekhnicheskoi Fiziki, Vol. 62, No. 2, pp. 27-33 (1992). In Russian. // Гайдуков Н.И. Гидродинамическая модель движения струи шаровой молнии через узкое отверстие плоского экрана. Журнал технической физики, Том 62, Выпуск 2, с. 27-33 (1992). http://journals.ioffe.ru/articles/viewPDF/24889.

57.    Stephan K.D. Electrostatic charge bounds for ball lightning models. Physica Scripta Vol. 77, No 3, 035504 (2008). https://doi.org/10.1088/0031-8949/77/03/035504.

58.    Gaidukov N.I. Steady-state motion of the ball lightning observed by M. T. Dmitriev at the Onega River. Zhurnal Tekhnicheskoi Fiziki, Vol. 64, No. 2, pp. 38-48 (1994). In Russian. // Гайдуков Н.И. Установившееся движение шаровой молнии, наблюдённой М.Т. Дмитриевым на реке Онеге. Журнал технической физики, Том 64, Выпуск 2, с. 38-48 (1994). http://journals.ioffe.ru/articles/viewPDF/18634.

59.    Grigor’ev A.I., Shiryaeva S.O. and Petrushov N.A. Electric charge of a lightning ball. Technical Physics, Vol. 61, pp. 1319-1327 (2016). https://doi.org/10.1134/S1063784216090085.

60.    Alanakyan Yu.R., Bulankin D.A., Pevgov V.G., Smirnov L.V., Tsvetkov A.A. About the Nature of Bead Lightning and Laboratory "Plasmoids". Doklady Physics, Vol. 65, Issue 1, pp. 1-4 (2020). https://doi.org/10.1134/S1028335820010036.

61.    Shoulders K.R. EV: A Tale of Discovery, Jupiter Technologies, Austin, Texas (1987).

62.    Davis E.W. Ball Lightning Study. Technical report AFRL 2002-0039 (2003). https://documents2.theblackvault.com/documents/usaf/AFRL_2002-0039_Ball_Lightning_Study.pdf.

63.    Hubler G.K. A Possible Heuristic Explanation of Exotic Vacuum Objects (EVO’s, Charge Clusters). Journal of Condensed Matter Nuclear Science. Vol. 36 (1), pp. 30–37 (2022). https://jcmns.scholasticahq.com/article/72586-a-possible-heuristic-explanation-of-exotic-vacuum- objects-evo-s-charge-clusters,

 

Источник: http://sergf.ru/bb.htm

На научный сайт