Journal
of Vectorial Relativity, 2008, Vol. 3, No 3, 30 - 35.
Mass,
Momentum and Energy of Gravitational Field
S.G. Fedosin
Perm
State University, Russia,
intelli@list.ru
ABSTRACT: The
energy of the gravitational field and the mass related to it are calculated.
The momentum of the gravitational field of a moving body and the appropriate mass
of the field are determined. Comparison of the given masses shows their
difference. The reasons of violation of relativity and equivalence principles
are discussed.
KEYWORDS: Gravitation; Field Energy;
Mass of the field.
PACS: 03.50.Kk ; 04.90.+e ; 95.30 Sf;
I.
INTRODUCTION
According to the General Theory of Relativity (GTR), energy of all kinds
contributes to gravitational mass of a body. The density of gravitational energy
in the Lorentz-invariant Theory of Gravity (LITG) according to [1], [2] is
equal:
,
(1)
where 
– gravitational constant,
– gravitational
field strength,
– the speed of gravitation propagation,
– gravitational torsion.
II.
ENERGY
Let's find gravitational energy 
for a rest
round body, when 
. With homogeneous matter density 
for the gravitational field
strength inside and outside of the body it is possible to write down:
,
,
where 
– current
radius,
– mass of the
body.
We substitute the strengths in (1) and then
integrate by volume:
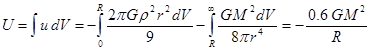, (2)
here 
– radius of the
body.
In (2) the basic contribution
to gravitational energy is given by the
energy of the field outside the body.
III.
MASS AND MOMENTUM DENSITY OF GRAVITATIONAL FIELD
Owing to interrelation between mass and energy we should expect, that
negative mass corresponds there to energy (2):
,
(3)
where 
– speed of light.
Due to mass 
there should be
reduction of the gravitational mass of the body in relation to initial mass .
Let's consider now a case when the body is moving with constant speed 
along axis Z. As far as the body is moving, that is
why 
and there is the
vector of momentum density of the gravitational field which is not equal to
zero:
.
(4)
It is convenient to find and through scalar 
and vector 
potentials of
the gravitational field. In LITG it is accepted, that:
,
. (5)
In their turn, potentials of the field outside the body are set taking into
account the delay of gravitational influence and consequently have the
Lorentz-invariant form:
,
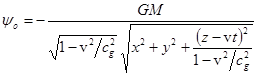. (6)
Substituting (6) in (5), we find:
, 
,
, 
, 
, 
.
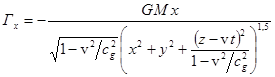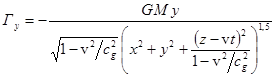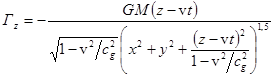It is evident, that 
. From all components of the vector 
from (4) only
the component directed along axis Z is important:
. (7)
Let's integrate 
by all points
of the field in space outside the body at the moment of time 
. We should consider the speed small in order
to neglect the Lorentz’s factor 
. As the round body is going, it seems flattened in
the direction of movement and turns into ellipsoid. In case of small speeds
this change of the form can be neglected. It is convenient to use spherical
coordinates:
, 
, 
.
Then for the field momentum outside the body we have:
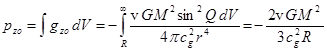. (8)
Inside the body within the limits of small speed the result is the
following:
, 
, 
.
The component of vector of momentum density of gravitational field
inside the body is calculated similarly (7). For the total momentum of the
field inside the body we get:
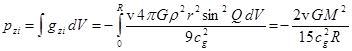. (9)
The sum of momentums of the field inside and outside the body with the
account (2) and (3) equals to:
. (10)
if 
.
The factor before the speed in (10) it is
natural to treat as the mass of the moving gravitational field related to the
body:
.
(11)
The mass of the field 
by absolute
value appears to be more, than mass of the
gravitational field of a motionless body.
IV.
DISCUSSION
As the mass of the field is included
into momentum of the gravitational field it can be considered inertial mass.
The mass of the field is connected
with the energy of motionless potential gravitational field and is related to
gravitational mass of the body. The inequality of masses and means
inapplicability of the principle of equivalence of inertial and gravitational
masses with respect to mass-energy of the gravitational field.
On the other hand, we find out also breaking of the traditional
relativity principle. Really, while the observer is motionless towards the
body, he fixes potential energy of the gravitational field and correspondingly
the mass of the field . As soon as the observer starts to move against the
body, he observes the changed mass of the body owing to the presence of the
momentum of the body in his reference system. Thereby the effective mass of the
body depends smoothly on the speed of movement of the observer against the
body, taking into account the Lorentz’s factor. But this does not apply to the
mass – it at once
increases in 4/3 times in relation to .
All aforesaid can be repeated
also concerning mass-energy of the electromagnetic field for the body having an
electric charge. Maybe equivalence and relativity principles should be
fulfilled only for the total mass-energy of the body including the energy of
rest of its constituent particles and binding energy of fields? But then we
should refuse from the superposition principle of field potentials and its
intensities, from the possibility of independent addition of energies of
various types and the masses corresponding to them.
We obtained the inequality of masses and on the basis of
the theory LITG. The equations of gravitational field in the theory are the following:
(12)
, 
,
where – the vector of
gravitational field strength,
– the solenoidal vector of
gravitational torsion or simply torsion,
– the gravitational
constant,
– the mass density,
– the vector of density of the mass current, dependent on the
speed of motion
of the mass element.
The equations (12) to within signs coincide with Maxwell equations for
an electromagnetic field. The density of energy of the field in electromagnetism
is equal:
, (13)
where E
– the vector of electric field strength,
B – the vector of magnetic
induction,
– the electric
constant,
c – the speed of propagation of
electromagnetic field (speed of light).
From comparison (13) and (1) it is visible, that these expressions also
have the identical form.
We should remind that in LITG the gravitational field is a real physical
field of fundamental type similar to electromagnetic field.
According to LITG, GTR has the function of describing the phenomena in noninertial reference systems. In order to find the correct
metrics of space-time deviated by fields, it is necessary in equations of
GTR to add energy-momentum stress tensor of gravitational field. This tensor is
defined in LITG in covariant form. The metrics found this way does not specify
the gravitational field, but the degree of deviation from the flat Minkowski space-time.
By the way in standard GTR the gravitational field is replaced with the
metric field having geometrical meaning. Then, perhaps, in standard GTR there
will be no difference between 
and 
? However, as it was already shown in a number of
works, for example in [3], [4], equations of GTR within the limits of a weak
field coincide with equations of LITG (12). Hence, the problem remains in GTR
too.
Most likely, the inequality of masses of the gravitational field is
connected neither with the special theory of relativity, nor with GTR.
Probably, the reason lies in the essence of the gravitational field. Let's
assume that gravitation between bodies is created due to effect of gravitons
streams. The fact, that the gravitation force and the mass of bodies does not
depend on their movement against streams of gravitons, we fix as the principle
of relativity. But the principle of relativity concerning mass of the field
does not work in the case when bodies do not change the movement against
streams of gravitons, but the observer does it. In this case the mass-energy of
the field connected with the body can not depend on
the state of movement of the observer. At the same time, the inequality of
masses 
and 
can reflect the
fact, that the inertial mass contains
additional mass of the field.
This additional mass, according to (11) equal to 
,
is connected with the moving body. Probably, it represents the energy
mass of excitation of the gravitational field, which is necessary to transfer a
body from the condition of rest in relation to the streams of gravitons, to a
certain condition of movement.
Let's notice, that finding the correlation between masses and we did not
specify the initial state of the body. Due to the principle of relativity, it
was insignificant for calculation , whether there the body was motionless in relation to
isotropic reference systems of gravitons streams or was moving together with
the observer against this reference system. But from the point of view of the
gravitation theory which is based on the concept of gravitons, it is important.
As when the body is moving against the streams of gravitons these streams
become nonisotropic, what can become the reason
appearing of the gravitational field momentum and of the additional mass of the
field .
But for an observer who is motionless in relation to the body, the
additional field mass
can not be found from the equations
of the field (this is the consequence of the relativity principle). From the
stated above it follows, that the distinction of inertial and gravitational
masses of the gravitational field can be explained by the existence of the
specific isotropic reference system. The feature of such reference system then
is isotropy of gravitons streams which are responsible for gravitation.
On falling of a
test body in the gravitational field of a massive body the graviton streams are
obviously not isotropic. In this case it is necessary to count, that the mass
of the gravitational field of the test body for an external observer is equal
to . For preservation of relativity and equivalence principles
it is also necessary to draw certain conclusions for the observer who is
motionless in relation to the test body. Though this observer finds the mass of
own gravitational field of the test body 
, but it is necessary to add to this mass the mass of
the field as the
consequence of movement of the test body under influence of attraction of the
massive body.
REFERENCES
1.
S G Fedosin. Fizika i filosofiia podobiia ot preonov do
metagalaktik. – Perm, Style-Mg, 1999, 544 pages. ISBN
5-8131-0012-1.
2.
S G
Fedosin. Electromagnetic
and Gravitational Pictures of the World. // Apeiron, Vol. 14, No. 4, P. 385-413, 2007.
3.
M Agop, C Gh
Buzea and B
Ciobanu. On Gravitational Shielding in
Electromagnetic Fields. – arXiv: physics / 9911011 v1,
4.
R P Lano. Gravitational
Meissner Effect. – arXiv: hep-th/9603077 v1,
Source: http://sergf.ru/masen.htm